工程弹塑性力学-第八章-2015[CompatibilityMode]详解
- 格式:pdf
- 大小:804.58 KB
- 文档页数:28





弹塑性力学引言一、固体力学在工程中的作用工程中的各种机械都是用固体材料制造而成的、各种结构物也都是用固体材料建造的。
为了使机械结构正常使用、实现其设计的功能,首先要保证它们在工作载荷与环境作用下不发生材料的破坏或影响使用的过大的变形,即保证它们具有足够的强度、刚度和稳定性。
在设计阶段,要根据要求实现的功能,对于设计的机械结构的形式按强度要求确定其各部分的形状和尺寸,以及所需选择的材料。
要完成这样的任务,首先要解决如下基本问题:在给定形状尺寸与材料的机械结构在设计规定载荷与环境(如温度)作用下所产生的变形与应力。
对于柔性结构,如细长梁、薄板、薄壳,以及它们的组合结构,还要分析其是否会丧失稳定性。
这些都是固体力学的基本问题。
如果机械结构所受载荷或环境的作用是随时间变化的,那么,它们的振动特性也对其性能有重要的影响。
在设计时往往要对其进行模态分析,求出影响最大的各个低阶固有频率与相应的振型,以确保不会与主要的激振载荷产生共振,导致过大的交变应力与变形,影响强度和舒适性。
有些情况下还要考虑它们在瞬态或冲击载荷作用下的瞬态响应。
这些也是固体力学的基本问题。
此外、许多机械零件和结构元件在制造工程中,采用各种成型工艺,材料要产生很大的塑性变形。
如何保证加工质量,提高形状准确性、减少残余应力、避免产生裂纹、皱曲等缺陷?如何设计加工用的各种模具,加工的压力,以及整个工艺流程,这里也都有固体力学问题。
正因为工程中提出了各种各样的固体力学问题,有时还有流体力学问题,在19世纪产生了弹性力学和流体力学,才导致力学逐渐从物理学中独立出来。
工程技术发展的要求是工程力学,包括固体力学、流体力学等发展的最重要的推动力。
而工程力学的发展则大大推动了许多工程技术的飞速发展。
因此,力学是许多工程部门设计研究人员的基本素质之一。
二、力学发展概况力学曾经是物理学的一个部分,最初也是物理学中最重要的组成部分。
力学知识最早起源于人们对自然现象的观察和在生产劳动中积累的经验。
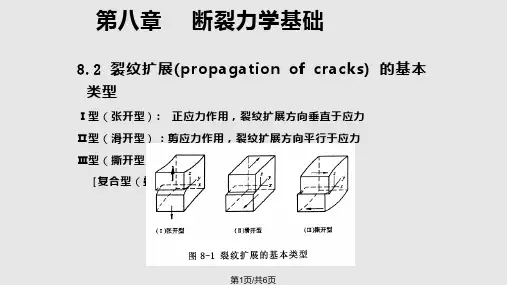


弹塑性力学弹塑性力学绪论:弹性力学也称弹性理论,主要研究弹性体在外力作用或温度变化等外界因素下所产生的应力、应变和位移,从而解决结构或机械设计中所提出的强度和刚度问题。
在研究对象上,弹性力学同材料力学和结构力学之间有一定的分工。
材料力学基本上只研究杆状构件;结构力学主要是在材料力学的基础上研究杆状构件所组成的结构,即所谓杆件系统;而弹性力学研究包括杆状构件在内的各种形状的弹性体。
弹塑性力学是固体力学的一个重要分支,是研究弹性和塑形物体变形规律的一门学科。
它推理严谨,计算结果准确,是分析和解决许多工程技术问题的基础和依据。
在弹塑性力学中,我们可以看到很多学习材料力学、结构力学等学科所熟知的参数和变量,一些解题的思路也很类似,但是我们不能等同的将弹塑性力学看成材料力学或者是结构力学来学习。
材料力学和结构力学的研究对象及问题,往往也是弹塑性力学所研究的对象及问题。
但是,在材料力学和结构力学中主要采用简化的初等理论可以描述的数学模型;在弹塑性力学中,则将采用较精确的数学模型。
有些工程问题(例如非圆形断面柱体的扭转、孔边应力集中、深梁应力分析等问题)用材料力学和结构力学的方法求解,而在弹塑性力学中是可以解决的;有些问题虽然用材料力学和结构力学的方法可以求解,但无法给出精确可靠的理论,而弹塑性力学则可以给出用初等理论所得结果可靠性与精确度的评价。
在弹塑性力学分析中,常采用如下简化假设:连续性假设、均匀各向同性、小变形假设、无初应力假设等假设。
弹塑性力学基本方程的建立需要从几何学、运动学和物理学三方面来研究。
在运动学方面,主要是建立物体的平衡条件,不仅物体整体要保持平衡,而且物体内的任何局部都要处于平衡状态。
反映这一规律的数学方程有两类,即运动微分方程和载荷的边界条件。
以上两类方程都与材料的力学性质无关,属于普适方程。
在物理学方面,则要建立应力与应变或应力与应变增量之间的关系,这种关系常称为本构关系,它描述材料在不同环境下的力学性质。


弹塑性力学讲义弹塑性力学1 弹塑性的概念所谓弹塑性指的是物体在外力作用下发生变形而外力除去后变形不能完全恢复的性质。
变形中可回复的部分称为弹性变形,变形中不可回复的部分称为塑性变形。
塑性变形总是在外力的作用超过一定的限度后出现。
2 简单拉压状态下金属材料弹塑性行为及其数学模型(1)理想塑性材料的弹塑性行为σs主要特点:屈服后加载,表现出一种流动变形现象,材料失去进一步承载的能力;屈服后卸载,应力应变增量大致与弹性变形段相同。
卸载至零后再次加载,应力应变关系相当于原应力应变关系曲线在应变轴方向作了一个平移,平移量为残余塑性应变。
数学表达:Eε(0 ε εs)σ σ(ε)σ(ε ε)s s Eε( εs ε 0)σ σ(ε)(ε εs) σs(2)线性强化材料的弹塑性行为σσs主要特点:屈服后加载,材料仍有进一步承载的能力,但应力应变增量的比例较弹性段小;屈服后卸载,应力应变增量大致与弹性变形段相同。
卸载至零后再次加载,屈服应力为卸载前的应力值(较先前的屈服应力大),应力应变关系相当于原应力应变关系曲线在应变轴方向作了一个平移,平移量为残余塑性应变,同时应力轴伸长。
两种常用的强化模型数学表达:Eε(0 ε εs)σ σ(ε)σ E(ε ε)(ε ε)ss sEε( εs ε 0)σ σ(ε)σs E(ε εs)(ε εs)上述描述弹塑性材料应力应变关系的数学模型称为全量型本构关系。
显然不能代表弹塑性变形规律的全貌。
它描述了单调应力-应变过程。
为了描述弹塑性力学行为的“过程相依”,需要建立增量型本构关系。
记当前应力为σ0,应力增量为dσ,应变增量为dε,分析弹塑性行为可以得出相应的增量变形法则。
理想塑性材料的增量型弹塑性关系(1)由dσ决定dε当σs σ0 σs时,dε dσ/E 当σ0 σs时,dεdλσ0ifdσ 0 dσ/Eifdσ 0dλσ0ifdσ 0当σ0 σs时,dεdσ/Eifdσ 0(2)由dε决定dσ当σs σ0 σs时,dσ Edε0ifdε 0当σ0 σs时,dσEdεifdε 0当σ0 σs时,dσ0ifdε 0 Edεifdε 0例:已经测得某理想弹塑性材料的细杆所经受的轴向应变过程如图所示,试求此杆中的应力过程。
第八章理想刚塑性的平面应变问题
8.5 典型的滑移线场
8.6 滑移线场的数值求解
8.7 楔体的单边受压
8.8 刚性压模的冲压问题
8.9圆形切口板条的极限拉力
8.10板条的抽拉拉
利用非线性的塑性本构关系求解问题,而是在研究了平面应变状态下塑性变形的一些特点后,将问题转为建立研究了滑移线的某些性质研究了滑移线的某些性质,建立了滑移线与塑性变形规律之间的联系,从而为求解工程实际问题提供了必要的依据。
解决塑性加工工艺中的题提供了有用的参考数据并为等课题的研究提供了有利的条件。
(4)与变形平面相平行的各层之间没有相对错动物体的各点位移发生在xoy 平面内:
(,)(,u u x y v v x y ==,x u x εε∂=
∂xy v x γ∂∂=+∂∂由(8.1)得应变分量:
3中间主应力
01(2z x σσσ==+因此,在平面塑性应变条件下,垂直于变形平面的法向应力等于平均应力。
min z σσσσ
==任意一点的应力状态都可以用平均应力τ来表示,最大剪应力所作用的面与应力主平面成45
3
s
k σ=
(σσ−x y 使用Tresa(特雷斯卡)屈服条件时,主应力表达式为:
121(22
x y σσσσσ+=±
2
s
k σ=
(σσ−x y 可见在塑性平面应变问题中,两种屈服条件的形式是
相同的,只是σs 前面的系数不同。
e
α
σn
a
y
στx
σx σ
O 1
σ3
σ1
σ2
滑移线法的原理及应用
3. 不同应力状态下莫尔圆的圆心坐标不同:
0z σσσ
==τ
3
σk
k
σ
o
大圆的直径为2k ,圆心的横坐标为σ。
由图中可见,最大切应力平面上正应力等于平均压力σ,即在塑性平面应变情况下,应力由σ和k 确定。
由于k 对于理想塑性材料是常数,因此只要找到平均应力σ,一点的应力状态便可以确定。
1
σ
滑移线法的原理及应用
4. 用平均应力σ与最大剪应力和x 轴夹角θ表示应力状态:
x
σ根据单元法线方向的平衡条件:
1
σ2
σϕ
τϕϕ22121
2
12121cos 21cos 2cos sin 22
11
()()cos 2cos 222
x ϕϕ
σσϕσϕσσσσσσϕστϕ+−=+=+=++−=+由垂直于法线方向上力的平衡条件得:
12cos sin cos sin ϕτσϕϕσϕϕ
=−121
()sin 2sin 2
σσϕτ=−=上述两式平方相加得:
22()x ϕσστ−+=
cos2x σσκ=+cos 2y σσκϕ=−i 上述两式平方相加得:
22()x ϕσστ−+=sin 2xy τκϕ
=cos 2xy τκθ
=1σσκ=+2σσκ=−z σσ
=X方向是主应力方向
位移分量:
(,)u u x y v ==,x u x εε∂=
∂xy v x γ∂∂=+∂∂几何分量:
(20ij y ε
=⎢∂∂⎢⎢&⎢⎣
由塑性增量理论的Levy—Mises 关系得:
(),(x x y ελσσελσ=−=&&&&ij ij
ελε=&&
y x
∂∂x v ∂∂+x ∂由材料的体积不可压缩性可得:
在塑性区由5个方程求5两个平衡方程(8.8),屈服条件(8.10),位移速度表示的本构方程将塑性区内各点最大剪应力的方向连接起来并绘成连续的曲线,则可以得到两族正交的曲线,这两族正交的曲线称为方向不同,一族曲线称为αα线
β顺时针
逆时针
(3)若应力场不同,则滑移线场亦不同。
滑移线场分布于整个变形体中,而且可以一直延伸到变形体的边界。
(4)在滑移线场中,任意点的最大剪应力都等于相同的值,即但是各点的平均正应力σ则不同。
利用滑移线场求解问题时,需要求出平均正应力σ和α族滑移线上切线与ctg dx βθ⎪
=−⎪⎭
族:
2(cos 2x x σθκθ∂∂−∂∂2(sin 2y x
σθκθ∂∂−∂∂dy
tg dx α=沿线:
积分
dy
dx β=−沿线: αβ沿线:
沿线:
写成改变量形式
xy x γ=∂(x x xy
xy σσσττ⎧=⎪
⎨
⎪=⎩0
z ε=dt ⎡∂1(2x ij v y ε⎢∂⎢
⎢∂=⎢∂⎢⎢⎢⎣
&应变率张量
中间主应力
2
z σσ==xz yz ττ==0,未知的应力分量只有注意到:(x x x s σσσ=−=−12222()2x y xy J s s s s ′=++=塑性区:刚性区:
y x v v y x
∂∂+∂∂在塑性区由5个方程求若采用Tresca 屈服条件其表达式与Mises 屈服条件相同。
n
τ+n
τΓn
σ−图8.1 刚塑性交界线
两侧应力间断值
sin 2cos 22
x y
nt xy σστϕτϕ
−=+τ若x,y方向为主方向
sin 2nt τκϕ
=cos2x σσκϕ=+cos 2y σσκϕ=−sin 2xy τκϕ
=n,t ⇒x,y
45°在与主应力σ1成45角的方向上:
(8.18)
x σσ
=y σσ=xy τκ
=2(sin 2cos y x
σθκθ∂∂−−∂∂O
x y
2
s 1
s L
取活动坐标∂∂∂∂
dy
tg dx α=沿线:
积分
dy
dx β=−沿线: αβ沿线:
沿线:
写成改变量形式
y x
∂∂0θ=代入
0,x
v x ∂=∂
x αβθ=∂∂
(sin cos )0v v y αβθθθ=+=∂0v v x x αβθ
∂∂−=∂∂0v v y y
βα
θ
∂∂+=∂∂或
θb
θa
θ图8.5 压力变化与角度变化之间的关系
1
()
21
C C αβσ⎨=+⎪⎪()4C C βαθκ
=
−⎪⎩(8.29)
,,,C C αβσθ过同一点的关系式
如果β1线沿任意α线转到β2线,同样可得:
11 2.1 1.222θθθθ⋅⋅−=−11 2.1 1.222
σσσσ⋅
⋅−=−(8.29)∼(8.32)表示单元网格四个结点上的应力和倾斜角的相互关系
1C β可算出
B 2
C σκθ−=α线:
B B α沿1线1
-2C C C ασκθ=1C α可算出
C σ即算出
同理,滑移线场内任何点的2C βσκθ+=如果在某些区域中两族滑移线是直线,则在这种区域中的应力是均匀分布的,并且参数C
说明A’B’亦
ABB A′′
在的全部区域中
z滑移先场由两族彼此正交的滑移线构成,布满整个塑性变形区。
y
α
−n
−θ
θψ
T
S 边界O
ψ图8.11 应力边界条件
2(θψ1t σσκ=+⎫
⎬
2t σσκ=−⎭
若:AB 边拉力<BC 边拉力
σ⇒0,sin 2()1ψθψ=⇒⇒=−−
:v
α=
刚性区域
:,
v v
αβ
塑性区域不全为
O
D
A
C
B
814
二、简单应力滑移场
图8.14 均匀应力和简单应力滑移线OBC区域:
紧接着均匀应力区的塑性区
和均匀应力场连接处应力导数发生跳跃;
点O处的σ是不确定的。
x
图8.15 轴对称应力滑移场
边界上r=R 处的ϕ角,在σϕ>σ例:图中A 点:0ϕγ=−ϕ=⇒沿α线:2,d d σκθθϕ==±;22d d d d d θϕσκθκϕ===
0σσσκ==+=二、求出各点的应力值及确定塑性极限荷载在OA边:1n 在边:沿BC线:
2d d σκθ
=−从点B到点C:22
d π
θγ=−s n D
p σσ
κ−==−在OD边:
沿α线:0
dv v d αβθ−=d 0
v α=ABCD边沿β线:0
dv v d βαθ=−=0
v α≡OD边
0,2
v ds d x αα≡=2(2v v dV x β
β∂∂==−2s x
d x α∂∂四、校核刚性区的条件
3
2,(8.47)4
γπ<对情形只能算是p 3
2,4
γπ≥对情形求出的解是完全解
x α速度场:
2AB A B A A ′′′+=⇒⇒速度要降低一半,即AB段速度的向上分量是V/2
ACB ⇒⇒区域的速度分布sin y v v v αθ=+
BCA 区域的速度场:
2v α=AB B A ′+两个完全解的滑移场的大小可以不同,而在两者都是塑性区的地方应力分布是相同的,对应的极限荷载也相同,但速度场有差别。