2021学年初中数学《位似》同步练习(三)含答案及解析

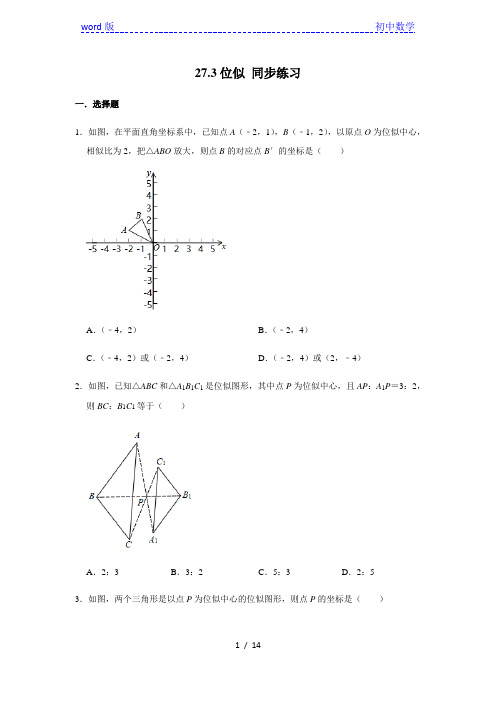
27.3位似同步练习一．选择题1．如图，在平面直角坐标系中，已知点A（﹣2，1），B（﹣1，2），以原点O为位似中心，相似比为2，把△ABO放大，则点B的对应点B′的坐标是（）A．（﹣4，2）B．（﹣2，4）C．（﹣4，2）或（﹣2，4）D．（﹣2，4）或（2，﹣4）2．如图，已知△ABC和△A1B1C1是位似图形，其中点P为位似中心，且AP：A1P＝3：2，则BC：B1C1等于（）A．2：3B．3：2C．5：3D．2：53．如图，两个三角形是以点P为位似中心的位似图形，则点P的坐标是（）A．（﹣3，2）B．（﹣3，1）C．（2，﹣3）D．（﹣2，3）4．如图，△ABC与△DEF位似，点O为位似中心．已知OA：OD＝1：2，则△ABC与△DEF的面积比为（）A．1：2B．1：3C．1：4D．1：55．如图，△ABC和△A1B1C1为位似图形，点O是它们的位似中心，点A为线段OA1的中点，若S△ABC＝2，则S△A1B1C1＝（）A．1B．2C．4D．86．如图，在直角坐标系中，△OAB的顶点为O（0，0），A（4，3），B（3，0）．以点O为位似中心，在第三象限内作与△OAB的位似比为的位似图形△OCD，则点C的坐标为（）A．（﹣1，﹣1）B．（﹣，﹣1）C．（﹣1，﹣）D．（﹣2，﹣1）7．在下列四个三角形中，与△ABC是位似图形且O为位似中心的是（）A．①B．②C．③D．④8．在平面直角坐标系中，已知点A（﹣4，2），B（﹣6，﹣4），以原点O为位似中心，相似比为，把△ABO缩小，则点B的对应点B′的坐标是（）A．（﹣3，﹣2）B．（﹣12，﹣8）C．（﹣3，﹣2）或（3，2）D．（﹣12，﹣8）或（12，8）9．如图，在平面直角坐标中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为，点A，B，E在x轴上．若正方形ABCD的边长为2，则点F坐标为（）A．（8，6）B．（9，6）C．D．（10，6）10．下列说法中，正确的个数是（）①位似图形一定是相似图形；②相似图形一定是位似图形；③两个位似图形若全等，则位似中心在两个图形之间；④若五边形ABCDE与五边形A'B'C'D'E'位似，则其中△ABC 与△A'B'C'也是位似的，且位似比相等．A．1B．2C．3D．4二．填空题11．如图，在平面直角坐标系中，△ABC与△DOE是位似图形．若A（0，3）、B（﹣2，0）、C（1，0）、E（6，0），△ABC与△DOE的位似中心是点M，则M点的坐标为．12．在平面直角坐标系中，将△AOB以点O为位似中心，为位似比作位似变换，得到△A1OB1，已知A（2，3），则点A1的坐标是．13．如图，在平面直角坐标系中，△ABC与△A1B1C1是位似图形，坐标原点O为位似中心．A与A1，B与B1是对应顶点．已知A（﹣6，2），A1（3，﹣1），BC＝5，则B1C1的长为．14．△ABC三个顶点的坐标分别为A（2，2），B（4，2），C（6，4）．以原点O为位似中心，将△ABC缩小得到△DEF，其中点D与A对应，点E与B对应，△DEF与△ABC对应边的比为1：2，这时点F的坐标是．15．如图，四边形OABC的顶点O为坐标原点，以O为位似中心，作出四边形OA1B1C1与四边形OABC位似，若A（6，0）的对应点为A1（4，0），四边形OABC的面积为27，则四边形OA1B1C1的面积为．三．解答题16．如图，正方形网格中，每个小正方形的边长都是一个单位长度，△ABC的顶点都在格点上．（1）以点O为位似中心，画出△ABC的位似图形△A1B1C1，使△ABC与△A1B1C1的位似比为1：2．（2）以点O为坐标原点，建立平面直角坐标系，若点M（a，b）在线段AC上，请直接写出点M经过（1）的位似变换后的对应点M'的坐标．17．如图，在由边长为1的小正方形组成的网格图中有△ABC，建立平面直角坐标系后，点O的坐标是（0，0）．（1）以O为位似中心，作△A′B′C′∽△ABC，相似比为1：2，且保证△A′B′C′在第三象限；（2）点B′的坐标为（，）；（3）△A′B′C′的面积是．18．图①、图②、图③都是6×6的网格，每个小正方形的顶点称为格点，△ABC的顶点A、B、C均在格点上，在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求作图．不要求写出画法．（1）在图①中画出△ABC边BC上的中线AD，则S△ABD＝；（2）在图②中画出△BEF，点E、F分别在边AB、BC上，满足△BEF∽△BAC，且S△BEF：S△BAC＝1：4；（3）在图③中画出△BMN，点M、N分别在边AB、BC上，使得△BMN与△BAC是位似图形，且点B为位似中心，位似比为．（保留作图痕迹）参考答案一．选择题1．解：∵以原点O为位似中心，相似比为2，将△OAB放大为△OA′B′，点B（﹣1，2），∴B′点的坐标为（﹣2，4）或（2，﹣4）．故选：D．2．解：∵△ABC和△A1B1C1是位似图形，∴△ABC∽△A1B1C1，AC∥A1C1，∴△APC∽△A1PC1，∴＝＝，∵△ABC∽△A1B1C1，∴＝＝，故选：B．3．解：如图点P为位似中心，∴＝，即＝，解得，PB＝3，∴点P的坐标为（﹣3，2），故选：A．4．解：∵△ABC与△DEF是位似图形，OA：OD＝1：2，∴△ABC与△DEF的位似比是1：2．∴△ABC与△DEF的相似比为1：2，∴△ABC与△DEF的面积比为1：4，故选：C．5．解：∵△ABC和△A1B1C1为位似图形，点O是它们的位似中心，点A为线段OA1的中点，∴＝（）2＝＝，∴S△A1B1C1＝8．故选：D．6．解：∵以点O为位似中心，位似比为，而A（4，3），∴A点的对应点C的坐标为（﹣，﹣1）．故选：B．7．解：∵②与△ABC相似，对应点的连线相交于点O，对应边互相平行，∴②与△ABC是位似图形且O为位似中心，故选：B．8．解：∵以原点O为位似中心，相似比为，把△ABO缩小，点B的坐标为（﹣6，﹣4），∴点B的对应点B′的坐标为（﹣6×，﹣4×）或（6×，4×），即（﹣3，﹣2）或（3，2），故选：C．9．解：∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为，∴＝＝，∵BC＝2，∴EF＝BE＝6，∵BC∥EF，∴△OBC∽△OEF，∴＝，解得：OB＝3，∴EO＝9，∴F点坐标为：（9，6），故选：B．10．解：①位似图形一定是相似图形，本说法正确；②相似图形不一定是位似图形，本说法错误；③两个位似图形若全等，则位似中心在两个图形之间，本说法正确；④若五边形ABCDE与五边形A'B'C'D'E'位似，则其中△ABC与△A'B'C'也是位似的，且位似比相等，本说法正确；故选：C．二．填空题11．解：过点D作DH⊥OE于点H，由题意可得：BC＝3，OE＝6，△ABC∽△DOE，则位似比为：3：6＝1：2，故OH＝2OB＝4，DH＝2OA＝6，则D点的坐标为：（4，6），由MO：MH＝1：2，MH＝MO+4，故MO：（MO+4）＝1：2，解得：MO＝4，则M点坐标为：（﹣4，0）．故答案为：（﹣4，0）．12．解：∵将△AOB以点O为位似中心，为位似比作位似变换，得到△A1OB1，A（2，3），∴点A1的坐标是：（×2，×3），即A1（，2）．故答案为：（，2）．13．解：∵△ABC与△A1B1C1是位似图形，坐标原点O为位似中心，A（﹣6，2），A1（3，﹣1），∴△ABC与△A1B1C1的相似比为：，∵BC＝5，∴B1C1的长为：5×＝．故答案为：．14．解：∵以原点O为位似中心，将△ABC缩小得到△DEF，△DEF与△ABC对应边的比为1：2，∴△DEF与△ABC的相似比为1：2，∵C（6，4）．∴点C的对应点F的坐标为（6×，4×）或（﹣6×，﹣4×）．即（3，2）或（﹣3，﹣2），故答案为：（3，2）或（﹣3，﹣2）．15．解：∵以O为位似中心，作出四边形OA1B1C1与四边形OABC位似，A（6，0）的对应点为A1（4，0），∴四边形OA1B1C1与四边形OABC的位似比为：4：6＝2：3，∴四边形OA1B1C1与四边形OABC的面积比为：4：9，∵四边形OABC的面积为27，∴四边形OA1B1C1的面积为：27×＝12．故答案为：12．三．解答题16．解：（1）如图，△A1B1C1为所作；（2）M'（﹣2a，﹣2b）．17．解：（1）如图，△A1B1C1即为所求；（2）由图可知，点B′的坐标为（﹣2，﹣1）．故答案为：﹣2，1；（3）△A′B′C′的面积是3×2﹣×2×1×2﹣×3×1＝2.5．故答案为：2.5．18．解：（1）如图①中，线段AD即为所求．S△ABD＝×3×4＝6，故答案为6．（2）如图②中，线段EF即为所求．（3）如图③中，线段MN即为所求．。

数学位似练习题初中
一、选择题
1. 若两个图形位似，且相似比为2:1，则下列哪个选项正确描述了它
们的性质？
A. 对应角相等，对应边成比例
B. 对应角不相等，对应边成比例
C. 对应角相等，对应边不成比例
D. 对应角不相等，对应边不成比例
2. 位似图形的中心称为位似中心，那么位似图形的位似中心具有什么
性质？
A. 位似中心是两个图形的公共点
B. 位似中心是两个图形的对称中心
C. 位似中心是两个图形的对应点连线的交点
D. 位似中心是两个图形的对应边的中点
二、填空题
3. 已知两个位似图形的相似比为3:1，那么它们的面积比为_________。

4. 若一个图形经过位似变换后，其边长扩大到原来的4倍，则其面积
扩大到原来的_________倍。

三、解答题
5. 给定一个三角形ABC，其位似图形A'B'C'与三角形ABC的相似比为4:1。

若三角形ABC的面积为24平方厘米，求三角形A'B'C'的面积。

6. 一个矩形的长和宽分别为6cm和4cm，求其经过位似变换后，相似
比为1:2，得到的新矩形的长和宽。

四、证明题
7. 证明：若两个图形位似，且位似比为k，则它们的面积比为k²。

8. 证明：若一个图形经过位似变换后，其边长扩大到原来的a倍，则其周长也扩大到原来的a倍。

以上练习题涵盖了位似图形的基本性质和计算，旨在帮助学生理解和掌握位似图形的概念及其应用。

通过这些练习，学生可以加深对位似图形相似比、面积比和周长比等概念的理解。

27.3 位似1. 如图（ 1）火焰的光芒穿过小孔O，在竖直的屏幕上形成倒立的实像，像的长度BD=2 cm，OA=60 cm, OB=1 5 cm，则火焰的长度为________.（ 1）（2）2.如图（2），五边形ABCDE 与五边形A′ B′ C′ D′ E′是位似图形，且位似比为1.若五2边形 ABCDE的面积为17 cm2，周长为20 cm，那么五边形 A′B′ C′ D′ E′的面积为________，周长为________.3.已知，如图 2，A′ B′∥ AB，B′ C′∥ BC，且 OA′∶ A′ A=4∶ 3，则△ ABC 与 ________是位似图形，位似比为________；△ OAB 与 ________是位似图形，位似比为________.图 24.以下说法中正确的选项是()A. 位似图形能够经过平移而相互获得B.位似图形的对应边平行且相等C.位似图形的位似中心不仅有一个D.位似中心到对应点的距离之比都相等5.小明在一块玻璃上画上了一幅画，而后用手电筒照着这块玻璃，将画映到雪白的墙上，这时我们以为玻璃上的画和墙上的画是位似图形. 请你再举出一些生活中的位似图形来？并说明一对对应线段的地点关系.6. 将有一个锐角为 30°的直角三角形放大，使放大后的三角形的边是原三角形对应边的3倍，并分别确立放大前后对应斜边的比值、对应直角边的比值.7. 一三角形三极点的坐标分别是A（0，0）， B（2，2）， C（3，1），试将△ ABC放大，使放大后的△ DEF与△ ABC对应边的比为2∶ 1. 并求出放大后的三角形各极点坐标.8、经过不一样位似中心将同一图形进行放大和减小，试问放大后的图形和减小后的图形可否也是位似图形？说说你的见解.答案： 1、 8 cm 2、17cm 210 cm 3、△ A′B′ C′7∶4 △OA′B′47∶ 4 4 、D 5 、略 6 、(1)1 ∶ 31∶ 37、位似中心取点不一样, 所得D、E、F各点坐标不一样，即答案不唯一.8、由放大或减小猴图形中对应线段与原图形中对应线段相互平行，故而放大后的图形和缩小后的图形的对应线段也相互平行，因此它们也是位似图形.。

2021 初三数学中考复习 图形的相似及位似 专题复习训练题1. △DEF ∽△ABC ，且∠A ＝50°，∠B ＝40°，那么∠F 的度数是( )A ．50B ．20°C ．70°D ．90°2. 在△ABC 中，BC ＝13，AC ＝11，AB ＝15，另一个与它相似的三角形的最大边长为10，那么它的最小边长为( )A.223B.203C.172D.1523. 如图，△ABC 中，E 是BC 中点，AD 是∠BAC 的平分线，EF ∥AD 交AC 于F.假设AB ＝11，AC ＝15，那么FC 的长为( )A ．11B ．12C ．13D ．144. 如图，小正方形的边长均为1，那么以下图中的三角形(阴影局部)与△ABC 相似的是( )5. 2x ＝3y(y≠0)，那么下面结论成立的是( )A.x y ＝32B.x 3＝2yC.x y ＝23D.x 2＝y 36. 如图，在△ABC 中，DE ∥BC ，AE ∶EC ＝2∶3，DE ＝4，那么BC 等于( )A ．10B ．8C ．9D ．67. 矩形的两边长分别为a ，b ，以下数据能构成黄金矩形的是( )A ．a ＝4，b ＝5＋2B ．a ＝4，b ＝5－2C ．a ＝2，b ＝5＋1D ．a ＝2，b ＝5－18. 如图，四边形ABCD 和A′B′C′D′是以点O 为位似中心的位似图形，假设OA∶OA′＝2∶3，那么四边形ABCD 与四边形A′B′C′D′的面积比为( )A ．4∶9B ．2∶5C ．2∶3 D.2∶ 39. 如图，△ABC 中，∠A ＝78°，AB ＝4，AC ＝6.将△ABC 沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是( )10. 以下图形中，是相似形的是( )A ．所有平行四边形B ．所有矩形C ．所有菱形D ．所有正方形11. 如图，△ADE ∽△ABC ，假设AD ＝1，AB ＝3，那么△ADE 与△ABC 的相似比是_________．12. 矩形ABCD 与矩形A ′B ′C ′D ′中，AB ＝40，BC ＝20，A ′B ′＝20，B ′C ′＝10，那么矩形ABCD 与矩形A ′B ′C ′D ′_______相似．(填“一定〞或“不一定〞)13. 在平面直角坐标系中，点C ，D 的坐标分别为C(2，3)，D(1，0)，现以原点为位似中心，将线段CD 放大得到线段AB.假设点D 的对应点B 在x 轴上且OB ＝2，那么点C 的对应点A 的坐标为 ．14. 如图，直线a ∥b ∥c ，直线l 1，l 2与这三条平行线分别交于点A ，B ，C 和点D ，E ，F.假设AB ∶BC ＝1∶2，DE ＝3，那么EF 的长为____．15. 如图，△AOB ∽△DOC ，OA ＝2，AD ＝9，OB ＝5，DC ＝12，∠A ＝58°，∠AOB ＝72°，求AB ，OC 的长和∠C 的度数．参考答案：1---10 DACBA ADACD11. 1:312. 一定13. (4，6)或(－4，－6)14. 615. 解：根据题意有：OD ＝AD －OA ＝7，OA OD ＝OB OC ＝AB CD ，∴OB OC ＝AB CD ＝27，∴5OC ＝AB 12＝27，∴OC ＝17.5，AB ＝247，∠C ＝∠B＝180°－∠A－∠AOB ＝50°。

华师大版数学九年级上册第23章图形的相似23.5位似图形同步练习一、选择题1. 下列说法不正确的是 （ ）A ．位似图形一定是相似图形 B. 相似图形不一定是位似图形C. 位似图形上任意一对对应点到位似中心的距离之比等于位似比D. 位似图形中每组对应点所在的直线必相互平行2、如图，线段CD 两个端点的坐标分别为C （1，2）、D （2，0），以原点为位似中心，将线段CD 放大得到线段AB ，若点B 坐标为（5，0），则点A 的坐标为（ ）A 、（2，5）B 、（2.5，5）C 、（3，5）D 、（3，6）3． 如图，点D E F ，，分别是()ABC AB AC >△各边的中点，下列说法中，错误．．的是（ ）A. AD 平分BAC ∠B. 12EF BC =C. EF 与AD 互相平分D.△DEF 是△ABC 的位似图形4、如图，△ABC经过位似变换得到△DEF ，点O是位似中心且OA=AD ，则△ABC与△DEF的面积比是（）A、1：6B、1：5C、1：4D、1：25、将一个菱形放在2倍的放大镜下，则下列说法中不正确的是（）A．菱形的边长扩大到原来的2倍 B．菱形的角的度数不变C．菱形的面积扩大到原来的2倍 D．菱形的面积扩大到原来的4倍6、如图，△DEF与△ABC是位似图形，点O是位似中心，D、E、F分别是OA、OB、OC的中点，则△DEF与△ABC的面积比是（）A、1：6B、1：5C、1：4D、1：27、如图，已知BC∥DE，则下列说法中不正确的是（）A．两个三角形是位似图形 B．点A是两个三角形的位似中心C．AE︰AD是位似比 D．点B与点E、点C与点D是对应位似点8、如图，线段AB的两个端点坐标分别为A（1，1），B（2，1），以原点O为位似中心，将线段AB放大后得到线段CD.若CD=2，则端点C的坐标为（）A、（2，2）B、（2，4）C、（3，2）D、（4，2）9、已知△ABC，以点A为位似中心，作出△ADE，使△ADE是△ABC放大2倍的图形，这样的图形可以作出个（）A．1个 B．2个 C．4个 D．无数个10、下列说法中：①位似图形一定是相似图形；②相似图形一定是位似图形；③两个位似图形若全等，则位似中心在两个图形之间；④若五边形ABCDE与五边形A′B′C′D′E′位似，则在五边形中连线组成的△ABC与△A′B′C′也是位似的.正确的个数是（）A、1B、2C、3D、411、如图所示，正方形EFGH是由正方形ABCD经过位似变换得到的，点O是位似中心，E ， F ， G ，H分别是OA ， OB ， OC ， OD的中点，则正方形EFGH与正方形ABCD的面积比是（）A 、1：6B 、1：5C 、1：4D 、1：212、 如图，以A 为位似中心，将△ADE 放大2倍后，得位似图形△ABC ，若1S 表示△ADE 的面积，2S 表示四边形DBCE 的面积，则21:S S =（ ）A ． 1︰2B ．1︰3C ．1︰4D ．2︰313、下列说法正确的是（ ）A 、两个位似图形对应点连线有可能无交点B 、两个位似图形对应点连线交点个数为1或2C 、两个位似图形对应点连线只有一个交点D 、两个位似图形对应点连线交点个数不少于4个14、用作位似形的方法，可以将一个图形放大或缩小，位似中心（ ）A 、只能选在原图形的外部B 、只能选在原图形的内部C 、只能选在原图形的边上D 、可以选择任意位置15、如图，四边形ABCD 与四边形AEFG 是位似图形，且AC ：AF=2：3，则下列结论不正确的是（）A、四边形ABCD与四边形AEFG是相似图形B、AD与AE的比是2：3C、四边形ABCD与四边形AEFG的周长比是2：3D、四边形ABCD与四边形AEFG的面积比是4：9二、填空题16、把一个正多边形放大到原来的2.5倍，则原图与新图的相似比为________．17、如果两个位似图形的对应线段长分别为3cm和5cm，且较小图形周长为30cm，则较大图形周长为 .18、△ABC中，点D、E、F分别是AB、BC、AC的中点，则与△ADF位似的三角形是________.19、雨后操场，小明从他前面2米远的一小块积水中看到了旗杆顶端的倒影，如果旗杆底端到积水的距离为20米，小明眼睛离地面1.5米，则旗杆的高度为．20、将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上，ABC的面积等于________；三、综合题21、如图，已知△ABC中，AB=12，BC=8，AC=6，点D、E分别在AB、AC上，如果以A、D、E为顶点的．三角形和以A、B、C为顶点的三角形相似，且相似比为13（1）根据题意确定D 、E 的位置，画出简图；（2）求AD 、AE 和DE 的长．22、如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的ABC △是格点三角形．在建立平面直角坐标系后，点B 的坐标为（11--，）．（1）把ABC △向左平移8格后得到111A B C △，画出111A B C △的图形并写出点1B 的坐标；（2）把ABC △绕点C 按顺时针方向旋转90o 后得到22A B C △，画出22A B C △的图形并写出点2B 的坐标；（3）把ABC △以点A 为位似中心放大，使放大前后对应边长的比为1:2，画出33AB C △的图形．23、如图，在平面直角坐标系中，四边形OABC的顶点坐标分别是O（0，0），A（3，0），B（4，4），C （-2，3），将点O ， A ， B ， C的横坐标、纵坐标都乘以-2.(1)画出以变化后的四个点为顶点的四边形；(2)由（1）得到的四边形与四边形OABC位似吗？如果位似，指出位似中心及与原图形的相似比.答案一、选择题1、B2、B3、C4、C5、D6、C7、C8、A9、C 10、C11、C 12、C 13、C 14、D 15、B二、填空题16、（2，-4）17、（-8，4）或（8，-4）.18、△ABC19、（0，2）（-4，0）..20、6三、综合题21、19．（1）两种情况，图略；（2）第一种情况：AD=4，AE=2，DE=83；第二种情况：AD=2，AE=4，DE=83．22、（1）画图略，点1B 的坐标为（9,1--）；（2）画图略，点2B 的坐标为（5,5）；（3）23、（1）解：如图所示，四边形OA′B′C′即为所求四边形；（2）解：∵将点O ， A ， B ， C的横坐标、纵坐标都乘以-2可得出四边形OA′B′C′，∴各对应边的比为2，对应点的连线都过原点，∴得到的四边形与四边形OABC位似，位似中心是O（0，0），与原图形的相似比为2. 【考点】作图-位似变换【解析】（1）将点O ， A ， B ， C的横坐标、纵坐标都乘以-2得O（0，0），A′（-6，0），B′（-8，-8），C′（4，-6），顺次连接各点即可；（2）根据位似图形的定义可知得到的四边形与四边形OABC位似，根据图形可得出位似中心及位似比.。

2022-2023学年人教版九年级数学下册《27.3位似》同步题型分类练习题（附答案）一．位似变换1．如图，已知△ABC与△DEF位似，位似中心为O，且△ABC的面积与△DEF的面积之比是16：9，则AO：AD的值为（）A．4：7B．4：3C．6：4D．9：52．如图平面直角坐标中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且位似比为，点A，B，E在x轴上，若正方形ABCD的边长为3，则F点坐标为（）A．（16.5，9）B．（18，12）C．（16.5，12）D．（16，12）3．在如图所示的网格中，以点O为位似中心，能够与四边形ABCD是位似图形的为（）A．四边形NGMF B．四边形NGME C．四边形NHMF D．四边形NHME 4．如图所示，在平面直角坐标系中，A（1，0），B（0，2），C（﹣2，1），以A为位似中心，把△ABC在点A同侧按相似比1：2放大，放大后的图形记作△A'B'C'，则C'的坐标为（）A．（﹣6，2）B．（﹣5，2）C．（﹣4，2）D．（﹣3，2）5．如图，在直角坐标系中，矩形ABCD与矩形EFGO位似，矩形ABCD的边CD在y轴上，点B的坐标为（﹣4，4），矩形EFGO的两边都在坐标轴上，且点F的坐标为（2，1），则矩形ABCD与EFGO的位似中心的坐标是．6．如图，平面直角坐标系中，点A在x轴正半轴上，且OA＝4，∠BOA＝30°，∠B＝90°，以点O为位似中心，在第一象限内将△AOB放大，使相似比为2：1，则点B的对应点B′的坐标为．7．如图，在平面直角坐标系中，A、B两点的坐标分别为A（﹣1，2）、B（0，2），C、D 两点的坐标分别为C（0，﹣1）、D（2，﹣1）．若线段AB和线段CD是位似图形，且位似中心在y轴上，则位似中心的坐标为．8．《墨子•天文志》记载：“执规矩，以度天下之方圆．”度方知圆，感悟数学之美．如图，正方形ABCD的面积为4，以它的对角线的交点为位似中心，作它的位似图形A'B'C'D'，若A'B'：AB＝2：1，则四边形A'B'C'D'的外接圆的周长为．9．如图，△ABC与△A1B1C1是以原点O为位似中心的位似图形，且位似比为1：2，则点A（1，2）在第一象限的对应点A1的坐标是．10．如图，在平面直角坐标系中，O是坐标原点，以点O为位似中心，△A1B1C1和△ABC 相似比为2：1，在网格中画出新图象△A1B1C1，若每个小正方形边长均为1，请写出A1，B1，C1的坐标．11．如图所示，由位似的正△A1B1C1，正△A2B2C2，正△A3B3C3，…正△A n B n∁n组成的相似图形，其中第一个△A1B1C1的边长为1，点O是B1C1中点，A2是OA1的中点，A3是OA2的中点…A n是OA n﹣1的中点，顶点B2，B3，…，B n．C2，C3，…，∁n都在B1C1边上．（1）试写出△A10B10C10和△A7B7C7的相似比和位似中心；（2）求出第n个三角形△A n B n∁n（n≥2）的周长．12．如图，△ABC中，P′是边AB上一点，四边形P'Q'M'N'是正方形，点Q'，M'在边BC上，点N′在△ABC内．连接BN′，并延长交AC于点N，过点N作NM⊥BC于点M，NP⊥MN交AB于点P，PQ⊥BC于点Q．（1）求证：四边形PQMN为正方形；（2）若∠A＝90°，AC＝1.5m，△ABC的面积＝1.5m2．求PN的长．13．（1）对数轴上的点P进行如下操作：先把点P表示的数乘以，再把所得数对应的点向右平移1个单位，得到点P的对应点P′．点A，B在数轴t，对线段AB上的每个点进行上述操作后得到线段A′B′，其中点A，B的对应点分别为A′，B′．如图1，若点A表示的数是﹣3，则点A′表示的数是，若点B′表示的数是2，则点B表示的数是；已知线段AB上的点E经过上述操作后得到的对应点E'点E重合，则点E表示的数是．（2）在平面直角坐标系xOy中，已知△ABC的顶点A（﹣2，0），B（2，0），C（2，4），对△ABC及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘以同个实数a，将得到的点先向右平移m单位，再向上平移n个单位（m＞0，n＞0），得到△A′B′C′及其内部的点，其中点A，B的对应点分别为A′（1，2），B′（3，2）．△ABC内部是否存在点F，使得点F经过上述操作后得到的对应点F′与点F重合，若存在，求出点F 的坐标；若不存在请说明理由．14．在平面直角坐标系中，抛物线L：y＝﹣x2+x+2与y轴交于点C，与x轴交于A、B两点（点A在点B的左侧）．（1）求A、B、C三点的坐标；（2）连接AC、BC，以点C为位似中心，将△ABC扩大到原来的2倍得到△A1B1C，其中点A1、B1分别是点A、B的对应点，如何平移抛物线L才能使其同时经过点A1、B1，求出所有的平移方式．二．作图-位似变换15．如图所示△DEF是△ABC位似图形的几种画法，其中正确的个数是（）A．4B．3C．2D．116．如图，在平面直角坐标系中，已知点O（0，0），A（6，0），B（0，8），以某点为位似中心，作出与△AOB的位似比为k的位似△CDE，则位似中心的坐标和k的值分别为（）A．（0，0），2B．（2，2），C．（2，2），2D．（1，1），17．如图，在坐标系中，以A（0，2）为位似中心，在y轴右侧作△ABC放大2倍后的位似图形△AB'C'，若C的对应点C'的坐标为（m，n），则点C的坐标为（）A．（m，n+3）B．（m，n﹣3）C．（m，n+2）D．（m，n﹣2）18．如图，以点O为位似中心，把△AOB缩小后得到△COD，使△COD∽△AOB，且相似比为，已知点A（3，6），则点C的坐标为．19．如图，以点O为位似中心，把△ABC放大2倍得到△A'B'C''，①AB∥A'B'；②△ABC∽△A'B'C'；③AO：AA'＝1：2；④点C、O、C'三点在同一直线上．则以上四种说法正确的是．20．如图，在平面直角坐标系中，矩形AOCB的两边OA，OC分别在x轴和y轴上，且OA ＝2．OC＝1，则矩形AOCB的对称中心的坐标是；在第二象限内，将矩形AOCB 以原点O为位似中心放大为原来的倍，得到矩形A1OC1B1，再将矩形A1OC1B1以原点O为位似中心放大倍，得到矩形A2OC2B2，…，按此规律，则矩形A4OC4B4的对称中心的坐标是．21．在平面直角坐标系中，△ABC的顶点A的坐标为（2，﹣5），若以原点O为位似中心，作△ABC的位似图形△A1B1C1，使△ABC与△A1B1C1的位似比为2：1，且点A1和点A 不在同一象限内，则点A1的坐标为．22．如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系，△ABC的三个顶点均在格点（网格线的交点）上．以原点O为位似中心，画△A1B1C1，使它与△ABC的相似比为2，则点B的对应点B1的坐标是．23．如图所示，在平面直角坐标系中，△ABC的顶点坐标分别是A（1，0），B（3，1），C （2，3）．请在所给直角坐标系中按要求画图和解答下列问题：（1）以原点O为位似中心，在原点的另一侧画出△ABC的位似三角形△DEF，△ABC 与△DEF的位似比为；（2）如果△ABC内部一点M的坐标为（a，b），请写出M的对应点M'的坐标（，）．24．如图，在平面直角坐标系网格中，将△ABC进行位似变换得到△A1B1C1．（1）在平面直角坐标系中画出位似中心；（2）设点P（a，b）为△ABC内一点，确定点P在△A1B1C1内的对应点P1的坐标．25．如图，小明在学习图形的位似时，利用几何画板软件，在平面直角坐标系中画出了△ABC的位似图形△A1B1C1．（1）在图中标出△ABC和△A1B1C1的位似中心M点的位置并写出M点的坐标．（2）若以点A1为位似中心，请你帮小明在图中画出△A1B1C1的位似图形△A2B2C2，且△A1B1C1与△A2B2C2的位似比为2：1．（3）直接写出（2）中C2点的坐标．26．如图，△ABC三个顶点分别为A（0，﹣3），B（3，﹣2），C（2，﹣4），正方形网格中，每个小正方形的边长是1个单位长度．（1）画出△ABC向上平移5个单位得到的△A1B1C1；（2）以点C为位似中心，在网格中画出△A2B2C2，使得△A2B2C2与△ABC位似，且△A2B2C2与△ABC的位似比为2：1，并写出A2的坐标．27．如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1）、B（﹣3，2）、C（﹣1，4）．（1）以原点O为位似中心，在第二象限内画出将△ABC放大为原来的2倍后的△A1B1C1．（2）画出△ABC绕O点顺时针旋转90°后得到的△A2B2C2．28．如图所示，图中的小方格都是边长为1的正方形，△ABC与△A'B'C'是以点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上．（1）画出位似中心点O；（2）直接写出△ABC与△A′B′C′的位似比；（3）以位似中心O为坐标原点，以格线所在直线为坐标轴建立平面直角坐标系，并直接写出△A′B′C′各顶点的坐标．参考答案一．位似变换1．解：∵△ABC与△DEF位似，∴△ABC∽△DEF，AC∥DF，∵△ABC的面积与△DEF的面积之比是16：9，∴＝，∵AC∥DF，∴△AOC∽△DOF，∴＝＝，∴AO：AD＝4：7，故选：A．2．解：∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且位似比为，∴＝＝，即＝＝，解得：EF＝12，OB＝4，∴F（16，12）．故选：D．3．解：如图，四边形ABCD的位似图形是四边形NGMF．故选：A．4．解：∵以A为位似中心，把△ABC按相似比1：2放大，放大后的图形记作△AB'C'，∴AC＝AC′，∴点C是线段AC′的中点，∵A（1，0），C（﹣2，1），∴C'的坐标为（﹣5，2）．故选：B．5．解：连接BF交y轴于点P，∵C和F是对应点，∴点P为位似中心，由题意得，GF＝2，AD＝4，GC＝4﹣1＝3，∵BC∥GF，∴△BPC∽△FPG，∴＝，即＝2，解得，GP＝1，∴OP＝2，∴位似中心的坐标是（0，2），故答案为：（0，2）．6．解：作BE⊥OA于E，则∠BEO＝90°，∵∠ABO＝90°，∠BOA＝30°，∴OB＝OA•cos30°＝4×＝2，∴BE＝OB＝，OE＝OB•cos30°＝2×＝3，∴点B的坐标为：（3，），∵以点O为位似中心，在第一象限内将△AOB放大，使相似比为2：1，∴点B的对应点B'的坐标为：（3×2，×2），即（6，2），故答案为：（6，2）．7．解：连接AD交BC于E，则点E为位似中心，∵A（﹣1，2）、B（0，2），C（0，﹣1）、D（2，﹣1）．∴AB＝1，CD＝2，BC＝3，∵线段AB和CD是位似图形，∴AB∥CD，∴＝，即＝，解得BE＝1，∴OE＝OB﹣BE＝1，∴位似中心点E的坐标为（0，1），故答案为：（0，1）．8．解：如图，连接B′D′．设B′D′的中点为O．∵正方形ABCD∽正方形A′B′C′D′，相似比为1：2，又∵正方形ABCD的面积为4，∴正方形A′B′C′D′的面积为16，∴A′B′＝A′D′＝4，∵∠B′A′D′＝90°，∴B′D′＝A′B′＝4，∴正方形A′B′C′D′的外接圆的周长＝4π，故答案为：4π．9．解：∵△ABC与△A1B1C1是以原点O为位似中心的位似图形，且位似比为1：2，∵A（1，2），点A（1，2）在第一象限的对应点是A1，∴点A1的坐标为：（2，4）．故答案为：（2，4）．10．解：如图，△A1B1C1即为所求，A1（0，8），B1（6，6），C1（6，2）．11．解：（1）∵△A1B1C1的边长为1，点O是B1C1中点，A2是OA1的中点，∴正△A2B2C2的边长为，正△A3B3C3的边长为（）2，正△A10B10C10和的边长为（）9，正△A7B7C7的边长为（）6，∴正△A10B10C10和正△A7B7C7的相似比＝＝；它们的位似中心为点O；（2）∵第n个三角形△A n B n∁n（n≥2）的边长为（）n﹣1，∴第n个三角形△A n B n∁n（n≥2）的周长为．12．（1）证明：∵NM⊥BC，NP⊥MN，PQ⊥BC，∴四边形PQMN为矩形，∵四边形P'Q'M'N'是正方形，∴PN∥P′N′，∴＝，∵MN∥M′N′，∴＝，∴＝，而P′N′＝M′N′，∴PN＝MN，∴四边形PQMN为正方形；（2）解：作AD⊥BC于D，AD交PN于E，如图，∵△ABC的面积＝1.5，∴AB•AC＝1.5，∴AB＝2，∴BC＝＝2.5，∵BC•AD＝1.5，∴AD＝＝，设PN＝x，则PQ＝DE＝x，AE＝﹣x，∵PN∥BC，∴△APN∽△ABC，∴＝，即＝，解得x＝，即PN的长为m．13．解：（1）点A′：﹣3×+1＝﹣1+1＝0，设点B表示的数为a，则a+1＝2，解得a＝3，设点E表示的数为b，则b+1＝b，解得b＝；故答案为：0，3，；（2）根据题意，得：，解得：，设点F的坐标为（x，y），∵对应点F′与点F重合，∴x+2＝x，y+2＝y，解得x＝y＝4，所以，点F的坐标为（4，4），∵点F的坐标为（4，4）不在△ABC内，故△ABC内部不存在点F，使得点F经过上述操作后得到的对应点F′与点F重合．14．解：（1）在y＝﹣x2+x+2中，令y＝0，即0＝﹣x2+x+2，解得：x1＝2，x2＝﹣1，∴A（﹣1，0），B（2，0），令x＝0，即y＝2，∴C（0，2）；（2）如图，当抛物线经过A1（2，6），B1（﹣4，6）时，设抛物线的解析式，y＝﹣x2+bx+c，则有，解得，，∴抛物线的解析式为y＝﹣x2﹣2x+14＝﹣（x+1）2+15，当抛物线经过A2（﹣2，﹣2），B2（4，﹣2）时，同法可得抛物线的解析式为：y＝﹣x2+2x+6＝﹣（x﹣1）2+7．∵原来的抛物线的解析式为y＝﹣（x﹣）2+，∴+1＝，15﹣＝，∴原来抛物线向左平移，再向上平移单位得到y＝﹣x2﹣2x+14．1﹣＝，7﹣＝，原来抛物线向右平移单位，再向上平移单位得到y＝﹣x2+2x+6．二．作图-位似变换15．解：第一个图形中的位似中心为A点，第二个图形中的位似中心为AD与BC的交点，第三个图形中的位似中心为O点，第四个图形中的位似中心为O点．故选：A．16．解：如图所示：位似中心F的坐标为：（2，2），k的值为：＝．故选：B．17．解：过点A作x轴的平行线DD′，作CD⊥DD′于D，作C′D′⊥DD′于D′，设C（x，y），则CD＝y﹣2、AD＝﹣x，C′D′＝2﹣n，AD′＝m，∵△AB′C′与△ABC的位似比为2：1，∴＝＝，即＝＝，解得：x＝﹣m，y＝﹣n+3，∴点C的坐标为（﹣m，﹣n+3），故选：A．18．解：由题意得，点A与点C是对应点，△AOB与△COD的相似比是3，∴点C的坐标为（3×，6×），即（1，2），当点C值第三象限时，C（﹣1，﹣2）故答案为：（1，2）或（﹣1，﹣2）．19．解：∵以点O为位似中心，把△ABC放大2倍得到△A'B'C''，∴AB∥A'B，△ABC∽△A'B'C'；AO：AA'＝2：1；点C、O、C'三点在同一直线上，①①②④正确，故答案为：①②④．20．解：∵OA＝2．OC＝1，∴B（﹣2，1），∴矩形AOCB的对称中心的坐标为（﹣1，），∵将矩形AOCB以原点O为位似中心放大为原来的倍，得到矩形A1OC1B1，∴B1（﹣3，），同理可得B2（﹣，），B3（﹣，），B4（﹣，），∴矩形A4OC4B4的对称中心的坐标是（﹣，）．故答案为（﹣1，），（﹣，）．21．解：在同一象限内，∵△ABC与△A′B′C′是以原点O为位似中心的位似图形，其中相似比是2：1，A坐标为（2，﹣5），∴则点A′的坐标为：（1，﹣2.5），不在同一象限内，∵△ABC与△A′B′C′是以原点O为位似中心的位似图形，其中相似比是2：1，A坐标为（2，﹣5），∴则点A′的坐标为：（﹣1，2.5），故答案为：（﹣1，2.5）．22．解：如图所示：△A1B1C1和△A′B′C′与△ABC的相似比为2，点B的对应点B1的坐标是：（4，2）或（﹣4，﹣2）．故答案为：（4，2）或（﹣4，﹣2）．23．解：（1）如图，△DEF即为所求；（2）M′（﹣2a，﹣2b）．故答案为：﹣2a，﹣2b．24．解：（1）如图点O即为位似中心；（2）设点P（a，b）为△ABC内一点，则点P在△A1B1C1内的对应点P1的坐标（2a，2b）．25．解：（1）如图，点M为所作，M点的坐标为（0，2）；（2）如图，△A2B2C2即为所求；（3）C2（﹣4，2）．26．解：（1）如图，△A1B1C1即为所求；（2）如图，△A2B2C2即为所求．A2的坐标（﹣2．，﹣2）．27．解：（1）如图，△A1B1C1即为所求；（2）如图，△A2B2C2即为所求．28．解：（1）如图，（2）2：1，（3）A′（﹣6，0），B′（﹣3，2），C′（﹣4，4）．。

27.3.1 位似图形基础训练知识点1 位似图形的定义1.下列各组图形中,不是位似图形的是( )2.图中两个四边形是位似图形,它们的位似中心是( )A.点MB.点NC.点OD.点P3.下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于位似比.其中正确命题的序号是( )A.②③B.①②C.③④D.②③④4.如图,在下列四种图形变换中,该图案不包括的变换是( )A.平移B.轴对称C.旋转D.位似5.如图,△OAB和△OCD是位似图形,则位似中心是_________,图中AB与CD的位置关系是_________.知识点2位似图形的性质6.两个图形中,对应点到位似中心的线段长之比为3∶2,则这两个图形的位似比为( )A.3∶2B.9∶4C.√3∶√2D.2∶17.如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,则△ABC与△DEF的面积之比为( )A.1∶2B.1∶4C.1∶5D.1∶68.如图,已知点M,N,P,Q分别为菱形ABCD四条边的中点,则下列说法中正确的是( )A.四边形MNPQ是菱形B.四边形MNPQ与菱形ABCD位似C.四边形MNPQ与菱形ABCD的周长之比为1∶2D.四边形MNPQ与菱形ABCD的面积之比为1∶2知识点3 位似图形的画法9.下面是△ABC位似图形的几种画法,其中正确的有( )A.1个B.2个C.3个D.4个10.利用位似图形将一个图形放大或缩小时,首先要选取一点作为位似中心,那么位似中心可以在( )A.图形外B.图形内C.图形上D.以上都可以11.如图,在正方形ABCD的边AB,BC,CD,DA上顺次截取AA'=BB'=CC'=DD',根据所学知识,我们知道四边形A'B'C'D'也是正方形,且正方形A'B'C'D'相似于正方形ABCD,其中点A与A',点B与B',点C与C',点D与D'是对应顶点,那么这两个正方形是位似图形吗?如果是位似图形,请找出位似中心;如果不是位似图形,请说明理由.提升训练考查角度1 利用位似图形的定义识别位似图形12.如图,哪些是位似图形?哪些不是位似图形?如果是位似图形,请找出各自的位似中心,并说明理由.考查角度2 利用位似图形的性质作图13.如图,已知四边形ABCD,将图形各边放大到原来的3倍.考查角度3 利用位似图形进行相关计算14.如图,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.(1)画出位似中心点O;(2)求出△ABC与△A'B'C'的位似比;(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于2.5∶1.考查角度4 利用位似图形的定义证明位似图形15.如图,点O是△ABC外的一点,分别在射线OA,OB,OC上取一点A',B',C',使得OA'OA =OB'OB=OC'OC=3.连接A'B',B'C',C'A',所得△A'B'C'与△ABC是否是位似图形?证明你的结论.考查角度5 利用位似图形的性质求线段长(方程思想)16.如图,矩形ABCD与矩形AB'C'D'是位似图形,A为位似中心.已知矩形ABCD的周长为24,BB'=4,DD'=2,求AB,AD的长.探究培优拔尖角度1 利用位似图形性质证等积式17.如图,已知△DEO与△ABO是位似图形,△OEF与△OBC是位似图形. 求证:OD·OC=OF·OA.拔尖角度2 利用位似图形的性质判断线段的位置关系18.如图,△ABC与△A'B'C'是位似图形,点A,B,A',B',O共线,点O为位似中心.(1)AC与A'C'平行吗?为什么?(2)若AB=2A'B',OC'=5,求CC'的长.拔尖角度3 利用位似图形的定义和性质探究与位似相关的问题19.如图,在所给网格图(每个小正方形的边长是1)中完成下列问题: (1)四边形ABCD与四边形A1B1C1D1关于直线MN成轴对称,请在图中画出对称轴并标注上相应字母M,N;(2)以图中O点为位似中心,将四边形ABCD放大,得到放大后的四边形A2B2C2D2,求四边形ABCD与四边形A2B2C2D2的对应边的比是多少. (3)求四边形A2B2C2D2的面积.参考答案1.【答案】B2.【答案】D3.【答案】D4.【答案】A5.【答案】点O;平行6.【答案】A7.【答案】B 8.【答案】D 9.【答案】C 10.【答案】D11.解:这两个正方形不是位似图形,因为它们对应点的连线所在的直线不交于同一点.易错总结:两个图形是位似图形的条件是:(1)它们是相似图形;(2)两个图形的对应点所在的直线相交于一点,即位似中心.本题中的两个正方形虽是相似图形,但无论顶点间是怎样的对应关系,其连线所在的直线都不交于同一点,因此它们不是位似图形.12.解:①③两组中的图形是位似图形,它们的位似中心分别为点O,O1.理由如下:根据位似图形的概念,如果两个图形不仅是相似图形,而且每组对应点所在的直线都相交于一点,那么这样的两个图形叫做位似图形.图①③都具备这个特点,而②中的两个图形不具备这个特点,所以②不是位似图形.方法总结:识别位似图形的方法:先判断两个图形是否相似,如果不是相似图形,则这两个图形不可能位似;如果相似,再判断这两个相似图形的每组对应点所在的直线是否都经过同一个点,若经过,可判断两个图形位似,否则两个图形不位似.13.解:方法一:位似中心在图形外,在图形的外面任选一点O,如图①.(1)作射线OA,OB,OC,OD,在这些射线上分别截取OA'=3OA,OB'=3OB,OC'=3OC,OD'=3OD.(2)顺次连接A',B',C',D',所得图形A'B'C'D'即为所求.方法二:位似中心在图形上,例如:以点B为位似中心,如图②.(1)延长BA,BC分别到A',C',使BA'=3BA,BC'=3BC.(2)连接BD 并延长到D',使BD'=3BD. (3)连接A'D',D'C',所得图形A'BC'D'即为所求.方法三:位似中心在图形内,在图形的内部任选一点O.请同学们自己试着做一做.点拨:作位似图形,关键是先选定位似中心的位置. 14.解:(1)位似中心点O 如图所示. (2)由图易知,OA=6,OA'=12, ∴OA OA'=612=12,∴△ABC 与△A'B'C'的位似比为1∶2. (3)△A 1B 1C 1如图所示.15.解:△A'B'C'与△ABC 是位似图形. 证明如下:由已知得OA'OA=OC'OC=OB'OB=3,∠AOC=∠A'OC',∴△AOC ∽△A'OC'. ∴OA OA'=ACA'C'.同理,△OBC ∽△OB'C',△OAB ∽△OA'B', ∴OB OB'=BC B'C',OBOB'=ABA'B'.∴ABA'B'=ACA'C'=BCB'C'.∴△A'B'C'∽△ABC.又直线AA',BB',CC'交于一点, ∴△A'B'C'与△ABC 是位似图形.16.解:设AB=x,AD=y,由矩形ABCD 的周长为24,得2(x+y)=24①.又∵矩形ABCD 与矩形AB'C'D'位似,∴AB AB'=ADAD',即xx+4=yy+2②.解由①②组成的方程组得{x =8,y =4,即AB,AD 的长分别为8和4.17.证明:∵△DEO 与△ABO 是位似图形,∴OD OA =OE OB.又∵△OEF 与△OBC 是位似图形, ∴OE OB =OF OC.∴OD OA =OFOC,即OD ·OC=OF ·OA. 18.解:(1)AC 与A'C'平行.理由:∵△ABC 与△A'B'C'是位似图形,∴AC 与A'C'为对应边,由位似的性质可知AC ∥A'C'.(2)∵△ABC 与△A'B'C'是位似图形,∴△ABC ∽△A'B'C', ∵AB=2A'B',∴AC=2A'C'.又∵点A,B,A',B',O 共线,AC ∥A'C', ∴△OAC ∽△OA'C'.∴OC=2OC'.又∵OC'=5,∴OC=10.∴CC'=OC-OC'=10-5=5. 19.解:(1)直线MN 如图所示.(2)易知AB=3√2,BC=√10,CD=√2,AD=√10,A 2B 2=6√2,B 2C 2=2√10,C 2D 2=2√2,A 2D2=2√10,所以ABA2B2=BCB2C2=CDC2D2=ADA2D2=12,即四边形ABCD与四边形A2B2C2D2对应边的比为1∶2.(3)S四边形A2B2C2D2=S△A2B2C2-S△A2C2D2=12×8×6-12×8×2=16.。

第8节图形的位似一、选择题1、下列说法中正确的是( )A. 位似图形可以通过平移得到B. 位似图形的对应边平行且相等C. 位似图形的位似中心不只有一个D. 位似中心到对应点的距离之比都相等2、两个位似图形的位似中心是指( )A. 对应边的延长线的交点B. 两个图形顶点连线的交点C. 对应角平分线的交点D. 对应顶点连线所在直线的交点3、下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于相似比.其中正确结论的序号是( )A. ②③B. ①②C. ③④D. ②③④4、下列图形中,不是位似图形的是()5、如图,以点O 为位似中心,将△ABC 放大得到△DEF.若AD=OA,则△ABC 与△DEF 的面积之比为( )A. 1∶2B. 1∶4C. 1∶5D. 1∶66、如图,在平面直角坐标系中,与△ABC 是位似图形的是( )A. ①B. ②C. ③D. ④7、在平面直角坐标系中,有两点 A(4,2),B(3,0),以原点为位似中心,把 AB 缩小为原来的21,得到线段 A'B'.正确的画法是( )8、如图,在边长为 1 的小正方形组成的网格中,建立平面直角坐标系,△ABO 与△A'B'O'是以点 P 为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点 P 的坐标为( )A. (0,0)B. (0,1)C. (-3,2)D. (3,-2)二、填空题9、如图,以O 为位似中心,将边长为 256 的正方形 OABC 依次作位似变换,经第一次变换后得正方形 OA 1B 1C 1,其边长 OA 1 缩小为 OA 的21,经第二次变换后得正方形 OA 2B 2C 2,其边长 OA 2缩小为OA 1 的21,经第三次变换后得正方形 OA 3B 3C 3,其边长 OA 3 缩小为 OA 2 的21,……,依此规律,经第 n 次变换后,所得正方形 OA n B n C n 的边长为正方形 OABC 边长的倒数,则 n= .10、如图,正方形 OABC 与正方形 ODEF 是位似图形,点 O 为位似中心,相似比为 1∶2,点 A 的坐标为(0,1),则点 E 的坐标是 .11、如图,已知矩形OABC 与矩形ODEF 是位似图形,点P 是位似中心,若点B 的坐标为(2,4),点E 的坐标为(-1,2),则点P 的坐标为.三、解答题12、如图所示,在△ABC 中,已知DE∥BC.(1)△ADE 与△ABC 相似吗?为什么?(2)它们是位似图形吗?如果是,请指出位似中心.13、如图,△DEF 是△ABC 经过位似变换得到的,位似中心是点O,请确定点O 的位置,如果OC=3.6 cm,OF=2.4 cm,求它们的相似比.14、如图,已知四边形ABCD,用尺规将它放大,使放大前后的图形对应线段的比为1∶2.(画出一种即可)15、如图,在 10×10 的正方形网格中,点 A,B,C,D 均在格点上,以点 A 为位似中心画四边形AB'C'D',使它与四边形 ABCD 位似,且相似比为 2. (1)在图中画出四边形 AB'C'D'; (2)填空:△AC'D'是 三角形.16、如图,在平面直角坐标系中,△ABC 和△A'B'C'是以坐标原点 O 为位似中心的位似图形,且点 B(3,1),B'(6,2).(1)请你根据位似的特征并结合点 B 与点 B'的坐标回答下列问题:①若点 A(25,3 ),则点 A'的坐标为;②△ABC 与△A'B'C'的相似比为 ;(2)若△ABC 的面积为 m,求△A'B'C'的面积.(用含 m 的代数式表示)17、已知△ABC 的三个顶点坐标如下表所示.(1)将下表补充完整,并在如图所示的平面直角坐标系中画出△ABC 和△A'B'C';(2)观察△ABC 与△A'B'C',写出关于这两个三角形的一个正确结论.18、如图,在平面直角坐标系中,△ABC 的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).(1)画出△ABC 关于x 轴对称的△A1B1C1;(2)以M 点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比为2∶1.19、(1)在如图所示的平面直角坐标系中描出点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0),按描点的顺序连线;(2)在如图所示的平面直角坐标系中描出点(0,0),(10,8),(6,0),(10,2),(10,-2),(6,0),(8,-4),(0,0),按描点的顺序连线;(3) (1)(2)中两个图形有什么特点?(从形状来回答)答:.答案1.D2.D3.A4.B5.B6.C7.D8.C9. 1610. (2,2)11. (-2,0)12. (1)△ADE 与△ABC 相似.理由: ∵DE∥BC,∴∠B=∠ADE,∠C=∠AED,∴△ABC∽△ADE.(2)是位似图形.由(1)知△ADE∽△ABC.∵△ADE 和△ABC 的对应顶点的连线BD,CE 所在的直线相交于点A,∴△ADE 和△ABC 是位似图形,位似中心是点 A.13. 连接AD,CF 交于点O,则点O 即为所求.∵OC=3.6 cm,OF=2.4 cm,∴OC∶OF=3∶2,∴△ABC 与△DEF 的相似比为3∶2.14.答案不唯一,以下仅供参考.解法一:延长AD 到点D1,使DD1=AD;连接AC 并延长到点C1,使CC1=AC;延长AB 到点B1,使BB1=AB. 连接D1C1,C1B1,则四边形AB1C1D1即为所求(如图).解法二:延长DA 到点D1,使AD1=2AD;连接CA 并延长到点C1,使AC1=2AC;延长BA 到点B1,使AB1=2AB.连接B1C1,C1D1,则四边形AB1C1D1即为所求(如图).解法三:任取一点O,连接OA 并延长到点A1,使AA1=OA,连接OB 并延长到点B1,使BB1=OB,连接OC 并延长到点C1,使CC1=OC,连接OD并延长到点D1,使DD1=OD,连接A1B1,B1C1,C1D1,D1A1,则四边形A1B1C1D1即为所求(如图).15.(1)如图所示:(2)∵AC'2=42+82=16+64=80,AD'2=62+22=36+4=40,C'D'2=62+22=36+4=40, ∴AD'=C'D',AD'2+C'D'2=AC'2,∴△AC'D'是等腰直角三角形.故答案为等腰直角.16. (1)①∵点 B(3,1),B'(6,2),∴△A'B'C'与△ABC 的相似比为 2,又点 A 的坐标为(25,3),∴点 A'的坐标为(5,6).②△ABC 与△A'B'C'的相似比为 1∶2. (2)又∵△ABC 的面积为 m,∴△A'B'C'的面积为 4m.17. (1)补充题表中数据如下表所示,图形如图所示.(2)△ABC∽△A'B'C'.(答案不唯一)18.(1)如图所示,△A1B1C1 即为所求.(2)如图所示,△A2B2C2 即为所求.19.(1)如图所示. (2)如图所示. (3)两个图形是以原点为位似中心的位似图形.。

2021人教版九年级下-----------位似图形同步训练一、选择题1. 下列各组图形中的两个三角形均满足△ABC∼△DEF，则这两个三角形不是位似图形的是( )A. B.C. D.2. 下列每组的两个图形不是位似图形的是（）A. B.C. D.3. 如图，△A′B′C′是△ABC以点O为位似中心经过位似变换得到的，若OA:OA′=5:3，则△ABC的面积与△A′B′C′的面积比是( )A.25:9B.5:9C.25:3D.5:34. △OAB的顶点坐标分别为O(0,0)，A(2,4)，B(4,0)，△OCD与△OAB关于，其中点C与点A是对应点，则点C的坐标是点O成位似关系，相似比为12( )A.(1,2)B.(4,8)C.(1,2)或(−1,−2)D.(4,8)或(−4,−8)5. 如图，网格中的两个三角形是位似图形，它们的位似中心是()A.点AB.点BC.点CD.点D6. 如图，在网格图中，以D为位似中心，把△ABC放大到原来的2倍，则点A的对应点为( )A.O点B.E点C.G点D.F点7. 如图，小正方形网格中的两个三角形是位似图形，它们的位似中心是( )A.点PB.点OC.点MD.点N8. 如图，以某点为位似中心，将△AOB进行位似变换得到△CDE，记△AOB与△CDE对应边的比为k，则位似中心的坐标和k的值分别为( )C.(2, 2)，2D.(2, 2)，3A.(0, 0)，2B.(2, 2)，129. 如图，点O是四边形ABCD内一点，A′,B′,C′,D′分别是OA,OB,OC,OD上的点，且OA′:A′A=OB′:B′B=OC′:C′C=OD′:D′D=2:1，若四边形A′B′C′D′的面积为12cm2，则四边形ABCD的面积为()A.18cm2B.27cm2C.36cm2D.54cm210. 如图，以点O为位似中心，将△ABC缩小后得△A′B′C′，已知OB=3OB′，则△A′B′C′与△ABC的面积比为（）A.1:3B.3:1C.9:1D.1:911. 在平面直角坐标系中，已知点E(−4,2)，F(−2,−2)，以原点O为位似中心，相似比为1:2，把△EFO缩小，则点E的对应点E′的坐标是（）A.(−2,1)B.(−8,4)C.(−8,4)或(8,−4)D.(−2,1)或(2,−1)12. 如图，以点O为位似中心，把△ABC放大为原图形的2倍得到△A′B′C′，若△ABC与△A′B′C′的位似比为k，则以下结论中正确的是（）A.k＝2B.k＝−2C.k=12D.k=−1213. 如图，以点O为位似中心，将△ABC缩小后得到△A′B′C′，若OB=30B′，则△A′B′C′与△ABC的面积比为()A.1:3B.1:4C.1:5D.1:914. 如图，△ABC与△A′B′C′是位似图形，点O是位似中心，若OA=2AA′，S△ABC=8，则S△A′B′C′=()A.9B.16C.18D.24二、填空题15. 如图，在平面直角坐标系中，以原点O为位似中心，相似比为3:1，将△ABC放大为△DEF，已知C(1,√2)，则点F的坐标为________.16. 在平面直角坐标系中，△ABO三个顶点的坐标分别为A(−2, 4)，B(−4, 0)，O(0, 0)．以点O为位似中心，把这个三角形缩小为原来的1，得2到△CDO，则点A的对应点C的坐标是________．17. 如图，△DEF是由△ABC经过位似变换得到的，点O是位似中心，D，E，F分别是OA，OB，OC的中点，则△DEF与△ABC的面积比是________．18. 如图，△ABC与△A′B′C′是位似图形，且顶点都在格点上，则位似中心的坐标是________．三、解答题19. 如图，已知O是坐标原点，B，C两点的坐标分别为(3, −1)，(2, 1)．(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍（即新图与原图的相似比为2)，画出图形；(2)分别写出B、C两点的对应点B′，C′的坐标．20. 如图，用下面的方法可以画△AOB的内接等边三角形，阅读后证明相应问题．画法：①在△AOB内画等边△CDE使点C在OA上，点D在OB上；②连结OE并延长，交AB于点E′，过点E′作E′C′ // EC，交OA于点C′，作E′D′ // ED，交OB于点D′；③连结C′D′，则△C′D′E′是△AOB的内接三角形．求证：△C′D′E′是等边三角形．21. 如图，在平面直角坐标系中，A(2, 1)、B(1, −2)．(1)画出△AOB向左平移2个单位长度，再向上平移1个单位长度后的△O1A1B1;(2)以原点O为位似中心，在y轴的右侧画出△OAB的一个位似△OA2B2，使它与△OAB的相似比为2:1;(3)判断△O1A1B1与△OA2B2是否关于某一点M为位似中心的位似图形？若是，请在图中标出位似中心M,并写出点M的坐标.参考答案与试题解析一、选择题1.【答案】B【解答】解：A，位似中心是点A，对应顶点B与E，C与F的连线经过点A，故选项A是位似图形；B，对应顶点B与E，C与F的连线不经过点A，故选项B不是位似图形；C，位似中心是点A，对应顶点B与E，C与F的连线经过点A，故选项C是位似图形；D，位似中心是AD的中点，对应顶点A与D，B与E，C与F的连线经过这个点，故选项D是位似图形.故选B.2.【答案】B【解答】解：对应顶点的连线相交于一点的两个相似多边形叫位似图形．据此可得A、C、D三个图形中的两个图形都是位似图形；而B的对应顶点的连线不能相交于一点，故不是位似图形．故选B．3.【答案】A【解答】解：由位似变换的性质可知，A′B′//AB，A′C′//AC，∴ △A′B′C′∼△ABC，∴ OA:OA′=5:3，∴ △A′B′C′与△ABC的面积的比25:9.故选A．4.【答案】C【解答】解：∴ 点A(2,4)，且△OCD与△OAB的位似比为12，∴ 2×12=1，4×12=2，∴ 当点A与点C在同一个象限时，点C的坐标为(1,2)；当点A与点C不在同一个象限时，点C的坐标为(−1,−2).故选C.5.【答案】【解答】如图，位似中心为点D．故选D．6.【答案】C【解答】解：如图，点A的对应点为G.故选C.7.【答案】A【解答】解：因为点P在对应点M和点N所在的直线上，所以点P是两个三角形的位似中心.故选A．8.【答案】C【解答】解：连结OD，AC，如图：易得交点是位似中心为(2, 2)，k=OA:CD=6:3=2.故选C．9.【答案】B【解答】解：∴ OA′:A′A=OB′:B′B=OC′:C′C=OD′:D′D=2:1，∴ OA′:OA=OB′:OB=OC′:OC=OD′:OD=2:3，∴ 四边形A′B′C′D′与四边形ABCD的位似比为：2:3，∴ 四边形A′B′C′D′与四边形ABCD的面积比为：4:9，∴ 四边形A′B′C′D′的面积为12cm2，∴ 四边形ABCD的面积为27cm2．故选B．10.【答案】D【解答】解：由位似变换的性质可知，A′B′ // AB，A′C′ // AC，∴ OA′OA =OB′OB=13，∴ A′C′AC =OA′OA=13，∴ △A′B′C′与△ABC的相似比为1:3，∴ △A′B′C′与△ABC的面积的比1:9，故选：D．11.【答案】A【解答】此题暂无解答12.【答案】C【解答】以点O为位似中心，把△ABC放大为原图形的2倍得到△A′B′C′，∴ △ABC∽△A′B′C′，且ABA′B′=12，∴ △ABC与△A′B′C′的位似比为12，13.【答案】D【解答】此题暂无解答14.【答案】C【解答】解：∴ △ABC与△A′B′C′是位似图形，∴ △ABC∽△A′B′C′，∴ S△ABC:S△A′B′C′=OA2:OA′2，∴ OA=2AA′，∴ OA:OA′=2:3，∴ 8:S△A′B′C′=4:9，∴ S△A′B′C′=18．故选C．二、填空题15.【答案】(3，3√2)【解答】解：由题意得：△ABC∼△DEF，DFAC=3，又∴ △ABC与△DEF位似，且两个图形在位似中心的同侧，C(1,√2)，∴ F(3,3√2).故答案为：(3,3√2).16.【答案】(−1, 2)或(1, −2)【解答】解：以原点O为位似中心，把这个三角形缩小为原来的12，点A的坐标为(−2, 4)，∴ 点C的坐标为(−2×12, 4×12)或(2×12, −4×12)，即(−1, 2)或(1, −2).故答案为：(−1, 2)或(1, −2).17.【答案】1:4【解答】解：∴ △DEF是由△ABC经过位似变换得到的，∴ △DEF∽△ABC，∴ S△DEF:S△ABC=(DEAB)2，∴ D，E，F分别是OA，OB，OC的中点，∴ DE:AB=1:2，∴ S△DEF:S△ABC=1:4．故答案为：1:4．18.【答案】(9, 0)【解答】解：由题图可知，直线AA′与直线BB′的交点坐标为(9, 0)，所以位似中心的坐标为(9, 0)．故答案为：(9, 0).三、解答题19.【答案】解：(1)△OB′C′是所求的三角形.(2)B′的坐标是(−6,2)，C′的坐标是(−4,−2)．【解答】解：(1)△OB′C′是所求的三角形.(2)B′的坐标是(−6,2)，C′的坐标是(−4,−2)．20.【答案】证明：∴ E′C′ // EC，E′D′ // ED，∴ △OCE∽△OC′E′，△ODE∽△OD′E′，∴ CE:C′E′=OE:OE′，DE:D′E′=OE:OE′，∠CEO=∠C′E′O，∠DEO=∠D′E′O，∴ CE:C′E′=DE:D′E′，∠CED=∠C′E′D′，∴ △CDE∽△C′D′E′，∴ △CDE是等边三角形，∴ △C′D′E′是等边三角形．【解答】证明：∴ E′C′ // EC，E′D′ // ED，∴ △OCE∽△OC′E′，△ODE∽△OD′E′，∴ CE:C′E′=OE:OE′，DE:D′E′=OE:OE′，∠CEO=∠C′E′O，∠DEO=∠D′E′O，∴ CE:C′E′=DE:D′E′，∠CED=∠C′E′D′，∴ △CDE∽△C′D′E′，∴ △CDE是等边三角形，∴ △C′D′E′是等边三角形．21.【答案】解：(1)(2)如图(3)如图所示，△O1A1B1与△OA2B2是关于M(−4,2)为位似中心的位似图形.【解答】解：(1)(2)如图(3)如图所示，△O1A1B1与△OA2B2是关于M(−4,2)为位似中心的位似图形.。

九年级数学上册第四章相似三角形4.7 图形的位似随堂练习（含解析）（新版）浙教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（九年级数学上册第四章相似三角形4.7 图形的位似随堂练习（含解析）（新版）浙教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为九年级数学上册第四章相似三角形4.7 图形的位似随堂练习（含解析）（新版）浙教版的全部内容。

4。

7__图形的位似1．下列关于位似图形的表述：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点,那么，这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于位似比．其中正确命题的序号是( A ）A．②③B．①②C．③④D．②③④2．如图4－7－1中两个四边形是位似图形，它们的位似中心是（ D )图4－7－1A．点M B．点NC．点O D．点P【解析】根据位似图形的定义:对应点的连线交于一点，交点就是位似中心．即位似中心一定在对应点的连线上．点P在对应点M和点N所在直线上,再连结另两个对应点，即可得出P为两图形的位似中心．故选D。

3．[2017·绥化]如图4－7－2,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的，若△A′B′C′的面积与△ABC的面积比是4∶9，则OB′∶OB为（ A )图4－7－2A．2∶3 B．3∶2C．4∶5 D．4∶9【解析】由位似变换的性质可知△A′B′C′∽△ABC。

∵△A′B′C′与△ABC的面积的比是4∶9，△A′B′C′与△ABC的相似比为2∶3，∴错误!＝错误!.4．如图4－7－3,在平面直角坐标系中，以原点O为位似中心，将△ABO的边长扩大到原来的2倍，得到△A′B′O。