梯形1-

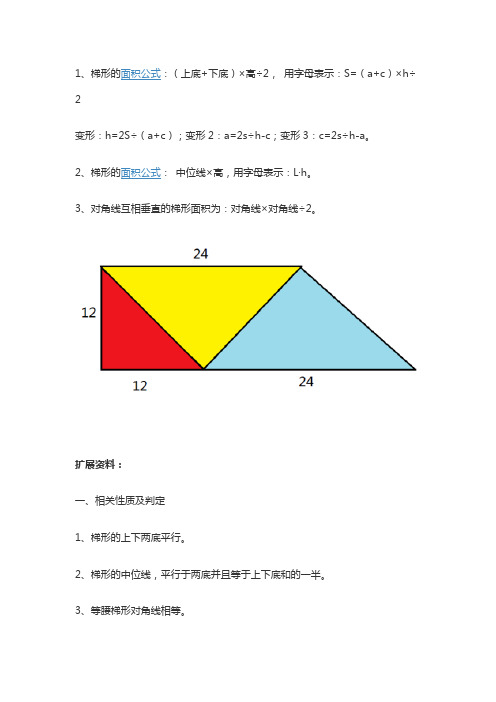
2变形：h=2S÷（a+c）；变形2：a=2s÷h-c；变形3：c=2s÷h-a。

2、梯形的面积公式：中位线×高，用字母表示：L·h。

3、对角线互相垂直的梯形面积为：对角线×对角线÷2。

扩展资料：一、相关性质及判定1、梯形的上下两底平行。

2、梯形的中位线，平行于两底并且等于上下底和的一半。

3、等腰梯形对角线相等。

判定：1、一组对边平行，另一组对边不平行的四边形是梯形。

2、一组对边平行且不相等的四边形是梯形。

二、周长公式1、梯形的周长公式：上底+下底+腰+腰，用字母表示：L=a+b+c+d2、等腰梯形的周长公式：上底+下底+2腰，用字母表示：a+c+2b。

三、常用辅助线1、平移一腰。

2、平移对角线。

3、反向延长两腰交于一点。

4、取一腰中点，另一腰两端点连接并延长。

5、取两底中点，过一底中点做两腰的平行线。

6、取两腰中点，连接，作中位线。

梯形的面积公式：面积=（上底＋下底）×高÷2上底即为梯形的上面边长，下底为下面边长，高为两个边长之间的距离。

具体如图所示：扩展资料：梯形的相关知识：定义：梯形是指只有一组对边平行的四边形。

平行的两边叫做梯形的底边，较长的一条底边叫下底，较短的一条底边叫上底。

另外两边叫腰；夹在两底之间的垂线段叫梯形的高。

一腰垂直于底的梯形叫直角梯形。

两腰相等的梯形叫等腰梯形。

等腰梯形是一种特殊的梯形。

性质：1、梯形的上下两底平行；2、梯形的中位线，平行于两底并且等于上下底和的一半；3、等腰梯形对角线相等。

判定：1、一组对边平行，另一组对边不平行的四边形是梯形。

2、一组对边平行且不相等的四边形是梯形。

2017年中考数学专项复习《梯形（1）》练习（无答案）浙教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017年中考数学专项复习《梯形（1）》练习（无答案）浙教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017年中考数学专项复习《梯形（1）》练习（无答案）浙教版的全部内容。

梯形（01）一、选择题1．如图的灰色小三角形为三个全等大三角形的重迭处，且三个大三角形各扣掉灰色小三角形后分别为甲、乙、丙三个梯形．若图中标示的∠1为58°，∠2为62°，∠3为60°,则关于甲、乙、丙三梯形的高的大小关系,下列叙述何者正确？( ）A．乙＞甲＞丙B．乙＞丙＞甲C．丙＞甲＞乙D．丙＞乙＞甲2．如图，梯形ABCD中，AD∥BC，E点在BC上，且AE⊥BC．若AB=10，BE=8,DE=6，则AD 的长度为( ）A．8 B．9 C．6D．63．如图，梯形ABCD中，AD∥BC，AB=，BC=4,连结BD，∠BAD的平分线交BD于点E,且AE∥CD，则AD的长为（)A．B．C．D．24．如图，已知等腰梯形ABCD中，AD∥BC，AB=DC，AC与BD相交于点O，则下列判断不正确的是（）A．△ABC≌△DCB B．△AOD≌△COB C．△ABO≌△DCO D．△ADB≌△DAC5．装有一些液体的长方体玻璃容器，水平放置在桌面上时，液体的深度为6，其正面如图1所示，将容器倾斜，其正面如图2所示．已知液体部分正面的面积保持不变,当AA1=4时，BB1=( ）A．10 B．8 C．6 D．46．如图，已知等腰梯形ABCD中，AD∥BC，AB=CD=AD=3，梯形中位线EF与对角线BD相交于点M，且BD⊥CD，则MF的长为（)A．1.5 B．3 C．3.5 D．4。

直角梯形的性质直角梯形是一个具有两个对角线互相垂直的四边形。

它的特点是有一对相邻边是平行的，同时有一个内角是直角（90度）。

在本文中，我们将探讨直角梯形的性质以及相关推论。

一. 基本性质直角梯形有以下基本性质：1. 对角线直角梯形有两条对角线，它们是互相垂直的。

如果我们将直角梯形的一个顶点作为原点，对角线分别为x轴和y轴，那么这两条对角线可以表示为x轴和y轴的方程：y = kx、y = -kx，其中k是一个常数。

2. 高直角梯形的高是指两条平行边之间的垂直距离。

可以通过计算两条平行边的长度差再除以2得到直角梯形的高：h = (b2 - b1) / 2，其中b1和b2分别表示两条平行边的长度。

3. 面积直角梯形的面积可以通过底边的长度和高来计算：A = (b1 + b2) *h / 2，其中b1和b2分别表示直角梯形的上底和下底的长度。

二. 相关推论在了解了直角梯形的基本性质之后，我们可以得出一些相关的推论。

1. 对角线长度根据勾股定理，直角梯形的两条对角线的长度可以通过上底、下底和高来计算：d1 = √(h^2 + b1^2)d2 = √(h^2 + b2^2)2. 角的性质直角梯形有若干个角，其中一个是直角（90度），另外三个角可以通过以下方式求得：∠A = ∠C = arctan((b2 - b1) / h)∠B = ∠D = 90度 - arctan((b2 - b1) / h)3. 周长直角梯形的周长可以通过上底、下底和两条腰的长度来计算：P = b1 + b2 + √(h^2 + (b2 - b1)^2)4. 内切圆和外切圆直角梯形的内切圆是唯一能够与直角梯形的四边都切于一点的圆，内切圆的半径可以通过直角梯形的高来计算：r = h直角梯形的外切圆是唯一能够同时切于直角梯形的四边的圆，外切圆的半径可以通过直角梯形的两条腰的长度之差和底边之和再除以2来计算：R = (|b2 - b1| + b1 + b2) / 2总结：直角梯形是一个具有特定性质的四边形，它的特点是一对相邻边平行且一对内角为直角。

梯形腰线长公式(一)
梯形腰线长公式
1. 梯形定义
梯形是一个四边形，两边是平行线段，另外两边不平行。

2. 梯形腰线
在梯形中，连接两个非平行边的线段叫做梯形的腰线。

3. 梯形腰线长公式
梯形的腰线长可以通过以下公式计算：
腰线长 = (底边1 + 底边2) × 高 / 2
其中，底边1和底边2分别表示梯形的两个平行底边的长度，高
表示梯形的高度。

4. 例子解释说明
例子1：
假设一个梯形的底边1长为10 cm，底边2长为8 cm，高为6 cm，我们可以使用梯形腰线长公式计算该梯形的腰线长：
腰线长 = (底边1 + 底边2) × 高 / 2
= (10 + 8) × 6 / 2
= 18 × 6 / 2
= 108 / 2
= 54 cm
因此，该梯形的腰线长为54 cm。

例子2：
再假设一个梯形的底边1长为15 cm，底边2长为12 cm，高为8 cm，使用梯形腰线长公式计算该梯形的腰线长：
腰线长 = (底边1 + 底边2) × 高 / 2
= (15 + 12) × 8 / 2
= 27 × 8 / 2
= 216 / 2
= 108 cm
因此，该梯形的腰线长为108 cm。

总结
梯形腰线长公式是一种计算梯形腰线长的常用公式，通过将梯形的两个底边长度和高度代入公式，可以简便地计算出梯形的腰线长。

无论底边长度和高度的数值如何变化，都可以通过该公式得出准确的结果。

梯形基本讲义（1）梯形基本讲义【课程导⼊】通过四边形的定义，引⼊梯形的种类及相关的性质和判定等知识。

【本课⽬标】1 、掌握四边形的定义。

2、梯形和等腰梯形的定义、性质和判定。

3 、会解决与梯形有关的实际问题。

【知识结构】1 、由不在同⼀直线上四条线段依次⾸尾相接围成的封闭的平⾯图形叫四边形。

2、梯形、等腰梯形的定义、性质和判定。

【重点知识解析】⼀、梯形及特殊梯形的定义梯形：⼀组对边平⾏⽽另⼀组对边不平⾏的四边形叫做梯形.（⼀组对边平⾏且不相等的四边形叫做梯形.）等腰梯形：两腰相等的梯形叫做等腰梯形.直⾓梯形：⼀腰垂直于底的梯形叫做直⾓梯形.⼆、等腰梯形的性质1、等腰梯形两腰相等、两底平⾏；2、等腰梯形在同⼀底上的两个⾓相等；3、等腰梯形的对⾓线相等；4 、等腰梯形是轴对称图形，它只有⼀条对称轴，⼀底的垂直平分线是它的对称轴.三、等腰梯形的判定1、两腰相等的梯形是等腰梯形；2、在同⼀底上的两个⾓相等的梯形是等腰梯形；3、对⾓线相等的梯形是等腰梯形例题精讲】A . 78°或1 20 ° B. 102 °或60°C. 120 °或78 °D. 60°或120°5. 等腰梯形上底长 2cm ，过它的⼀个端点引⼀腰的平⾏线与下底相交，所得三⾓形的周长为长为（A . 12cmB . 10cmD . 9cm例 3. 直⾓梯形的⼀腰与底边夹⾓为 60°，此腰与上底的长都是 8cm ，则梯形的周长是 ___________ .例4.如图，梯形ABCD 中，AD // BC , DE//AB , ADEC 的周长为10cm , BE 5cm ，则梯形ABCD 的周长为 _______ ；例 5.如图，梯形 ABCD 中，AB//CD , ACB 90° ,AC 平分 BAD , D 120 ° ,CD = 3cm ，则梯形的周长为 _______ cm ；1. 等腰梯形的上底、下底、⾼之⽐为 1 : 3 : 1，则下底⾓的度数是（）2. 3. A . 30°B ．45C ．60D ．75等腰梯形 ABCD 中， AD// BC ， AC 与 BD 交于 O 点，图中全等三⾓形有（） A .两对B .四对C ⼀对D .三对等腰梯形中，下列判断正确的是（ A .两底相等B .两个⾓相等C .同底上两底⾓互补D .对⾓线交点在对称轴上4. 已知梯形的两个对⾓分别是78 °和120 °，则另两个⾓分别是（）例 2. 在周长为30cm 的梯形ABCD 中，上底CD 5cm , DE//BC ，交AB 于E,则△ADE 的周长为cm ；6cm ，则梯形的周C . 8cm例 6.如图，A ABC 中，AB AC , BD、CE分别为ABC、形.例7.如图，在梯形ABCD 中，AB // DC, DA 丄AB, B 45°,延长CD到点E，使DE DA，连接AE .(1)求证：AE // BC ;(2 )若AB 3, CD 1，求四边形ABCE的⾯积.例8.在直⾓梯形ABCD中，AB//CD , AD CD , AB课后检测BC，⼜AE BC 于E,求证：CD CE .ACB的平分线，求证：四边形EBCD为等腰梯A mn c、选择题1. 在等腰梯形中，下列结论：①两腰相等；②两底平⾏；③对⾓线相等；④两底⾓相等.其中正确的有（2. 下列说法正确的是3 .梯形中位线长为12cm，⼀条对⾓线把中位线分成1 : 3两部分，则梯形的两底分别为（）A. 4cm 、8cmB. 9cm 、15cmC. 10cm 、14cmD. 6cm 、18cm4、下列命题中的假命题是（）A、等腰梯形在同⼀底边上的两个底⾓相等B、对⾓线相等的四边形是等腰梯形C、等腰梯形是轴对称图形D、等腰梯形的对⾓线相等5、给出下列四个命题（）⑴⼀组对边平⾏的四边形是平⾏四边形⑵⼀条对⾓线平分⼀个内⾓的平⾏四边形是菱形⑶两条对⾓线互相垂直的矩形是正⽅形⑷顺次连接等腰梯形四边中点所得四边形是等腰梯形。