MATLAB中常见的结构动力学分析技巧

如何使用Matlab进行材料力学与结构强度分析Matlab在材料力学与结构强度分析领域中扮演着重要的角色，它的强大功能和灵活性使其成为研究者和工程师们的首选工具。

本文将介绍如何利用Matlab进行材料力学和结构强度分析，并探讨其在实际应用中的优势和局限性。

1. 引言材料力学与结构强度分析是工程力学领域的重要研究方向，涉及到材料的性能评估、结构的设计与分析等方面。

Matlab作为一种高级编程语言和环境，提供了丰富的工具箱和函数，可以帮助研究者和工程师们实现对材料力学和结构强度的准确分析。

2. 材料力学分析2.1 弹性力学弹性力学是材料力学分析的基础，研究材料受力时的弹性变形和应力分布。

在Matlab中，可以利用矩阵运算和符号运算工具箱进行弹性力学的计算和求解。

通过定义材料的力学参数和边界条件，可以得到具体的变形和应力分布情况。

2.2 塑性力学塑性力学研究材料在受力超过弹性限度后的塑性变形和应力分布。

Matlab中提供了不同的塑性模型，如线性硬化、非线性硬化等，可以模拟材料的塑性行为。

通过调用相应的函数和工具箱，可以进行塑性力学的计算和分析。

2.3 破裂力学破裂力学研究材料在受到极限负荷时的破坏行为。

Matlab中提供了许多破裂准则和断裂模型的函数和工具箱，可以帮助研究者分析材料的断裂特性。

通过计算破坏应力强度因子和裂纹扩展速率等参数，可以评估材料的破裂性能。

3. 结构强度分析3.1 结构力学结构力学研究材料在受到外部载荷时的力学行为，包括结构的静力学和动力学分析。

通过使用Matlab提供的结构力学工具箱，研究者和工程师可以对结构进行受力分析和变形计算。

可以得到结构的应力分布、变形情况以及安全性评估等结果。

3.2 结构优化结构优化是利用数学方法和计算工具改善结构设计的过程。

Matlab提供了多种优化算法和函数，可以对结构进行形状优化、材料选择优化等。

通过设置优化目标和约束条件，可以得到最优的结构设计方案。

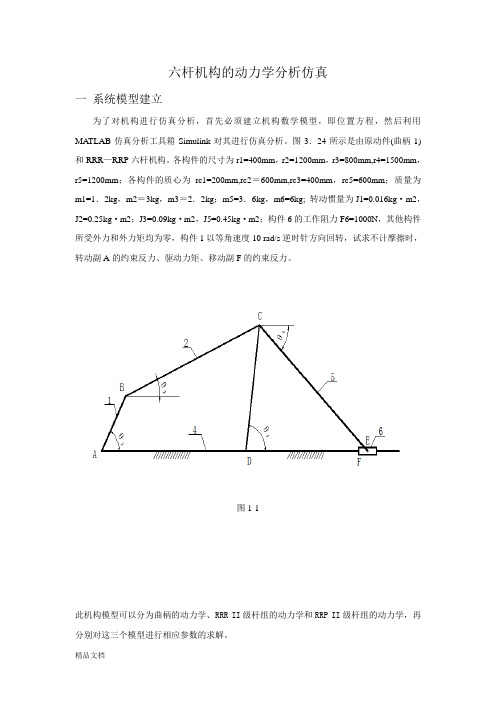
六杆机构的动力学分析仿真一系统模型建立为了对机构进行仿真分析，首先必须建立机构数学模型，即位置方程，然后利用MATLAB仿真分析工具箱Simulink对其进行仿真分析。

图3．24所示是由原动件(曲柄1)和RRR—RRP六杆机构。

各构件的尺寸为r1=400mm，r2=1200mm，r3=800mm,r4=1500mm，r5=1200mm；各构件的质心为rc1=200mm,rc2＝600mm,rc3=400mm，rc5=600mm；质量为m1=1．2kg，m2＝3kg，m3＝2．2kg；m5=3．6kg，m6=6kg; 转动惯量为J1=0.016kg·m2，J2=0.25kg·m2；J3=0.09kg·m2，J5=0.45kg·m2；构件6的工作阻力F6=1000N，其他构件所受外力和外力矩均为零，构件1以等角速度10 rad/s逆时针方向回转，试求不计摩擦时，转动副A的约束反力、驱动力矩、移动副F的约束反力。

图1-1此机构模型可以分为曲柄的动力学、RRR II级杆组的动力学和RRP II级杆组的动力学，再分别对这三个模型进行相应参数的求解。

图1-2 AB 构件受力模型如上图1-2对于曲柄AB 由理论力学可以列出表达式：111XA Re R ••=+-s m F R X XB 111y A Im R ••=+-s m F R y yB1111111111111cos )(sin )(cos sin ••=---+-++θθθθθJ r r R r r R r R r R M M c yB c XB c yA c XA F由运动学知识可以推得：)cos()2/cos(Re Re 12111111πθθπθθ++++=•••••••c c r r A s )sin()2/sin(Im Im 12111111πθθπθθ++++=•••••••c c r r A s将上述各式合并成矩阵形式有，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-+++++-++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡••••••••••g m R F r m r m A m R F r m r m A m M R R yB y c c XBX c c yA XA 111211111111112111111111)sin()2/sin(Im )cos()2/cos(Re πθθπθθπθθπθθ(1-21)如图1-3，对构件BC 的约束反力推导如下，图1-3 BC 构件受力模型222Re ••=++s m R F R XC X XB 2222Im ••=-++s m g m R F R yC y yB2222222222222cos )(sin )(cos sin ••=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yB c XB如图1-4，对构件BC 的约束反力推导如下，图 1-4 CD 构件受力模型333Re ••=-+s m R F R XC X XD 3333Im ••=-++s m g m R F R yC y yD3333333333333cos )(sin )(cos sin ••=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yD c XD由运动学可以推导得，)sin()2/sin(Im Im 22222222πθθπθθ++++=•••••••c c r r B s )cos()2/cos(Re Re 22222222πθθπθθ++++=•••••••c c r r B s )cos()2/cos(Re Re 32333333πθθπθθ++++=•••••••c c r r D s )sin()2/sin(Im Im 32333333πθθπθθ++++=•••••••c c r r D s将上述BC 构件，CD 构件各式合并成矩阵形式有，⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------33333333332222222222cos sin cos )(sin )(0010100001010000cos )(sin )(cos sin 001010000101θθθθθθθθc c c c c c c c r r r r r r r r r r r r ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡yD XD yC XC yB XB R R R R R R =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-+-++++-++++-+-++++-++++••••••••••••••••••••••••3333332333333333323333333322222222222222222222222222)sin()2/sin(Im )cos()2/cos(Re )sin()2/sin(Im )cos()2/cos(Re M J g m F r m r m D m F r m r m D m M J g m F r m r m B m F r m r m B m y c c X c c y c c X c c θπθθπθθπθθπθθθπθθπθθπθθπθθ (1-22)如图1-5 对构件5进行约束反力的推导如下，图1-5 CE 杆件受力模型••=++s m R F R xE x xC Re 55 ••=-++s m g m R F R yE y yC Im 5555555555555555cos )(sin )(cos sin ••=-+-+--θθθθθJ r r R r r R r R r R M c yE c xE c yC c xC如图1-6 对滑块进行受力分析如下，滑块受力模型••=--E m R R F F xE x Re sin 666θ ••=-+-E m g m R R F F yE y Im cos 6666θ由运动学可推，)cos()2/cos(C Re Re 5255555πθθπθθ•••••••+++=c c r r s )sin()2/sin(C Re Im 5255555πθθπθθ•••••••+++=c c r r s66cos Re θ••••=s E 66sin Im θ••••=s E⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+---+-++++-++++=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------••••••••••••••••g m F s m F s m M J g m F r m r m m F r m r m m R R R R R r r r r r r y x y c c x c c F yE xE yC xC c c c c 66666666655555525555555555255555555665555555555sin cos )sin()2/sin(C Re )cos()2/cos(C Re cos 1000sin 01000cos )(sin )(cos sin 010*******θθθπθθπθθπθθπθθθθθθθθ（1-23）二编程与仿真利用MATLAB进行仿真分析，主要包括两个步骤：首先是编制计算所需要的函数模块，然后利用其仿真工具箱Simulink建立仿真系统框图，设定初始参数进行仿真分析。

MATLAB在地震工程与结构动力学中的应用技术地震工程与结构动力学是研究地震对建筑物和结构物产生的振动和影响的学科领域。

它旨在通过分析和模拟地震荷载对建筑物和结构物的影响，从而更好地设计和构建能够抵御地震的建筑和结构。

在这个领域，MATLAB成为了一个非常重要的工具，用于模拟、计算和分析地震荷载和结构响应。

一、地震荷载的模拟和分析地震荷载是地震对建筑物和结构物施加的力量，它是地震工程与结构动力学中的重要研究内容之一。

MATLAB通过其强大的计算和数值模拟功能，为地震荷载的模拟和分析提供了良好的支持。

地震荷载的模拟通常基于地震波形的生成。

地震波是地震时地壳中产生的波动，能够传播到地表并对建筑物和结构物产生影响。

MATLAB可以使用其信号处理工具箱中的函数生成各种类型的地震波形，包括正弦波、脉冲波和复杂波形。

通过调整不同的参数，如频率、振幅和周期，可以生成不同性质的地震波形，模拟各种地震情况。

地震荷载的分析通常包括对地震波形的特征和响应的计算。

MATLAB提供了一系列的函数和工具箱，用于计算地震波形的频谱、振动周期和加速度等数据。

这些数据可以帮助工程师评估地震荷载对建筑物和结构物的影响程度，进而更好地设计和规划建筑物。

二、结构响应的模拟和分析结构响应是指建筑物和结构物在受到地震荷载作用时的动态响应。

MATLAB在模拟和分析结构响应方面也发挥了重要的作用。

MATLAB可以通过有限元分析（FEA）进行结构的动力学模拟。

有限元法是一种常用的数值计算方法，用于求解连续介质的力学问题。

通过将建筑物和结构物离散为有限数量的单元，并建立单元之间的相互关系和连接，可以模拟和计算其在地震等加载条件下的响应。

MATLAB提供了一个强大的有限元分析工具箱，可以支持复杂结构的模拟和分析。

在结构响应的分析中，MATLAB还提供了许多函数和工具箱，用于计算和分析结构的振动特性。

这些函数可以计算结构的频谱、振动模态和振型等数据，从而帮助工程师评估结构的抗震性能。

工程构件受力和刚度计算的MATLAB分析法工程构件受力和刚度计算是结构设计和分析中非常重要的一部分，它涉及到对构件受力和刚度进行计算的理论基础和方法。

而MATLAB作为一种广泛应用于科学计算和工程领域的软件工具，其强大的数学和算法功能使得其成为进行工程构件受力和刚度计算的理想选择。

在进行工程构件的受力和刚度计算时，首先需要建立合适的受力与形变模型。

其次，需要根据受到的外力和形变条件，建立构件的力平衡方程和形变方程。

最后，利用MATLAB的数值计算功能，对这些方程进行求解，以获得构件的受力和刚度。

在进行受力计算时，常用的方法包括静力方法、动力方法和有限元方法等。

其中，静力方法基于构件的受力平衡条件，通过求解受力方程组得到构件的受力分布。

动力方法则基于构件的振动特性，利用动力学方程求解得到构件的受力状态。

而有限元方法则是将结构离散为有限数量的单元，通过求解单元的刚度矩阵和载荷矩阵得到整个结构的受力情况。

在进行刚度计算时，常用的方法包括弹性刚度法和刚度矩阵法等。

其中，弹性刚度法是基于构件材料的弹性行为，通过求解弹性力学方程得到构件的刚度。

刚度矩阵法则是将结构离散为有限数量的节点，通过求解节点的刚度矩阵和载荷矩阵得到整个结构的刚度。

利用MATLAB进行工程构件受力和刚度计算时，用户可以编写自定义的函数和脚本来实现对受力和刚度方程的求解。

MATLAB提供了丰富的数学函数和工具箱，包括线性方程组的求解、特征值和特征向量的计算、矩阵运算等功能，这些功能可以大大简化受力和刚度计算的过程。

用户可以使用MATLAB的函数库来进行构件的受力和刚度计算，也可以根据实际需要进行函数的编写和修改。

总之，MATLAB分析法在工程构件受力和刚度计算中具有广泛的应用前景。

它通过提供强大的数学和算法功能，简化了受力和刚度计算的过程，并且可以根据实际需要进行函数的编写和修改。

工程师和科研人员可以利用MATLAB进行受力和刚度计算，以实现对工程构件的准确设计和分析。

Matlab中的结构动力学分析技术近年来，结构动力学分析在工程领域中扮演着越来越重要的角色。

随着计算机技术的不断发展，人们对于结构的振动响应和动态特性的研究越来越深入。

而Matlab作为一种强大的数值计算工具，为结构动力学分析的研究提供了非常有力的支持。

一、Matlab在结构动力学模型建立中的应用Matlab的强大计算能力和丰富的数学函数库使得模型的建立变得简单而直观。

通过编程和调用库函数，我们可以轻松地搭建起复杂的结构模型。

比如，利用Matlab的有限元分析库，我们可以轻松地建立三维体系的有限元模型，并进行节点位移和应变的计算。

其次，Matlab还支持多种计算方法，如频谱分析、时间域分析、模态分析等。

对于结构的动态响应分析，这些方法可以提供不同的视角和角度，并给出准确的结果。

借助Matlab的强大计算能力和多种分析方法，我们可以深入研究结构的力学特性和动力学行为。

二、Matlab在结构动力学特性计算中的应用结构的动力学特性是工程分析和设计的重要基础，如模态参数、频率响应等。

Matlab提供了多种计算工具和函数，可以帮助我们快速准确地计算这些特性。

首先，针对模态参数的计算，Matlab提供了函数可以实现特征值问题的求解。

通过调用这些函数，我们可以得到结构体系的自振频率和振型。

这些参数对于结构的设计和评估非常重要，可以帮助我们解决结构的共振问题，选择适当的减振措施。

此外，Matlab还支持用于分析频率响应的传递函数法和频率响应函数法。

通过这些方法，我们可以计算结构在不同频率下的响应，并进一步分析结构的受力情况和振动幅值。

这些分析结果可以为结构的优化设计和性能改进提供重要参考。

三、Matlab在结构动力学仿真分析中的应用Matlab还支持结构动力学的数值仿真分析，并能够提供丰富的可视化效果。

通过编写代码，我们可以模拟结构在不同加载条件下的动态响应，并观察和分析结构的变形和应力分布。

此外，Matlab还支持多种数值求解方法，如差分法、积分法、牛顿法等。

六杆机构的动力学分析仿真一系统模型建立为了对机构进行仿真分析，首先必须建立机构数学模型，即位置方程，然后利用MATLAB 仿真分析工具箱Simulink对其进行仿真分析。

图3．24所示是由原动件(曲柄1)和RRR—RRP 六杆机构。

各构件的尺寸为r1=400mm，r2=1200mm，r3=800mm,r4=1500mm，r5=1200mm；各构件的质心为rc1=200mm,rc2＝600mm,rc3=400mm，rc5=600mm；质量为m1=1．2kg，m2＝3kg，m3＝2．2kg；m5=3．6kg，m6=6kg; 转动惯量为J1=0.016kg·m2，J2=0.25kg·m2；J3=0.09kg·m2，J5=0.45kg·m2；构件6的工作阻力F6=1000N，其他构件所受外力和外力矩均为零，构件1以等角速度10 rad/s逆时针方向回转，试求不计摩擦时，转动副A的约束反力、驱动力矩、移动副F的约束反力。

图1-1此机构模型可以分为曲柄的动力学、RRR II级杆组的动力学和RRP II级杆组的动力学，再分别对这三个模型进行相应参数的求解。

图1-2 AB 构件受力模型如上图1-2对于曲柄AB 由理论力学可以列出表达式：111XA Re R ∙∙=+-s m F R X XB 111y A Im R ∙∙=+-s m F R y yB1111111111111cos )(sin )(cos sin ∙∙=---+-++θθθθθJ r r R r r R r R r R M M c yB c XB c yA c XA F由运动学知识可以推得：)cos()2/cos(Re Re 12111111πθθπθθ++++=∙∙∙∙∙∙∙c c r r A s )sin()2/sin(Im Im 12111111πθθπθθ++++=∙∙∙∙∙∙∙c c r r A s将上述各式合并成矩阵形式有，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-+++++-++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∙∙∙∙∙∙∙∙∙∙g m R F r m r m A m R F r m r m A m M R R yB y c c XBX c c yA XA 111211111111112111111111)sin()2/sin(Im )cos()2/cos(Re πθθπθθπθθπθθ(1-21)如图1-3，对构件BC 的约束反力推导如下，图1-3 BC 构件受力模型222Re ∙∙=++s m R F R XC X XB 2222Im ∙∙=-++s m g m R F R yC y yB2222222222222cos )(sin )(cos sin ∙∙=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yB c XB如图1-4，对构件BC 的约束反力推导如下，图 1-4 CD 构件受力模型333Re ∙∙=-+s m R F R XC X XD 3333Im ∙∙=-++s m g m R F R yC y yD3333333333333cos )(sin )(cos sin ∙∙=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yD c XD由运动学可以推导得，)sin()2/sin(Im Im 22222222πθθπθθ++++=∙∙∙∙∙∙∙c c r r B s )cos()2/cos(Re Re 22222222πθθπθθ++++=∙∙∙∙∙∙∙c c r r B s )cos()2/cos(Re Re 32333333πθθπθθ++++=∙∙∙∙∙∙∙c c r r D s )sin()2/sin(Im Im 32333333πθθπθθ++++=∙∙∙∙∙∙∙c c r r D s将上述BC 构件，CD 构件各式合并成矩阵形式有，⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------33333333332222222222cos sin cos )(sin )(0010100001010000cos )(sin )(cos sin 001010000101θθθθθθθθc c c c c c c c r r r r r r r r r r r r ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡yD XD yC XC yB XB R R R R R R =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-+-++++-++++-+-++++-++++∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3333332333333333323333333322222222222222222222222222)sin()2/sin(Im )cos()2/cos(Re )sin()2/sin(Im )cos()2/cos(Re M J g m F r m r m D m F r m r m D m M J g m F r m r m B m F r m r m B m y c c X c c y c c X c c θπθθπθθπθθπθθθπθθπθθπθθπθθ (1-22)如图1-5 对构件5进行约束反力的推导如下，图1-5 CE 杆件受力模型∙∙=++s m R F R xE x xC Re 55 ∙∙=-++s m g m R F R yE y yC Im 5555555555555555cos )(sin )(cos sin ∙∙=-+-+--θθθθθJ r r R r r R r R r R M c yE c xE c yC c xC如图1-6 对滑块进行受力分析如下，滑块受力模型∙∙=--E m R R F F xE x Re sin 666θ ∙∙=-+-E m g m R R F F yE y Im cos 6666θ由运动学可推，)cos()2/cos(C Re Re 5255555πθθπθθ∙∙∙∙∙∙∙+++=c c r r s )sin()2/sin(C Re Im 5255555πθθπθθ∙∙∙∙∙∙∙+++=c c r r s66cos Re θ∙∙∙∙=s E 66sin Im θ∙∙∙∙=s E⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+---+-++++-++++=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙g m F s m F s m M J g m F r m r m m F r m r m m R R R R R r r r r r r y x y c c x c c F yE xE yC xC c c c c 66666666655555525555555555255555555665555555555sin cos )sin()2/sin(C Re )cos()2/cos(C Re cos 1000sin 01000cos )(sin )(cos sin 010*******θθθπθθπθθπθθπθθθθθθθθ（1-23）二编程与仿真利用MATLAB进行仿真分析，主要包括两个步骤：首先是编制计算所需要的函数模块，然后利用其仿真工具箱Simulink建立仿真系统框图，设定初始参数进行仿真分析。

matlab newmark法Matlab Newmark法是一种非线性动力学分析方法，主要用于求解动力学系统的时间响应。

该方法由Newmark在20世纪50年代提出，在工程结构领域得到了广泛应用。

本文将分步骤回答关于Matlab Newmark法的问题，包括算法原理、计算步骤、优缺点以及实际案例的应用。

一、算法原理1.1 基本原理Matlab Newmark法是一种基于离散时间步长的计算方法。

其基本原理是通过将系统的运动方程转化为等效的一阶微分方程组，然后使用步进法进行数值求解。

该方法采用了二阶精度的数值积分公式，具有较高的计算精度和稳定性。

1.2 新马克法公式Matlab Newmark法的核心公式为：δu(t+Δt) = u(t) + Δt * v(t) + Δt^2 * (0.5 - β) * a(t)δv(t+Δt) = v(t) + Δt * (1 - γ) * a(t)δa(t+Δt) = (1 - γ) * a(t) + γ* a(t+Δt)其中，δ表示增量，u(t)、v(t)和a(t)分别表示位移、速度和加速度在时间t的值，β和γ为Newmark法的两个参数。

二、计算步骤2.1 确定系统参数首先，需要确定系统的质量矩阵、刚度矩阵和阻尼矩阵，以及外部激励载荷等参数。

2.2 确定时间步长根据求解精度和计算效率的要求，选择合适的时间步长Δt。

2.3 初始化位移、速度和加速度给定初始位移、速度和加速度的值。

2.4 进行时间循环使用Newmark法的公式，根据当前时刻的位移、速度和加速度的值，计算下一时刻的位移、速度和加速度。

2.5 判断收敛条件在每个时间步长内，判断计算结果是否满足收敛要求。

如果满足要求，则继续计算下一个时间步长；如果不满足要求，则重新选择适当的步长，并重新进行计算。

2.6 输出结果将每个时间步长内计算得到的位移、速度和加速度的值保存起来，以获取系统的时间响应曲线。

三、优缺点3.1 优点Matlab Newmark法具有以下优点：- 可以处理复杂的非线性动力学系统。

基于MATLAB/Solidworks COSMOSMotion的平面连杆机构动力学分析07208517王锡霖4-23在图示的正弦机构中,已知l AB =100 mm,h1=120 mm,h2 =80 mm,W1 =10 rad/s(常数)，滑块2和构件3的重量分别为G2 =40 N和G3 =100 N,质心S2 和S3 的位置如图所示，加于构件3上的生产阻力Fr=400 N，构件1的重力和惯性力略去不计。

试用解析法求机构在Φ1=60°、150°、220°位置时各运动副反力和需加于。

构件1上的平衡力偶Mb分别对三个构件进行受力分析如图：构件3受力图构件2受力图构件1受力图（1）滑块2：V S2 =L AB W1 ①a s2 = L AB W12②构件3：S=L AB sinΦ1 ③V3=L AB W1 COSΦ1 ④a3=-L AB W12 sinΦ1 ⑤(2)确定惯性力：F12=m2as2=(G2/g)LABW12 ⑥F13=m3a3=(G3/g)LABW12sinΦ1 ⑦(3)各构件的平衡方程：构件3：∑Fy=0,FR23 =Fr-F13∑Fx=0,FR4’=FR4∑MS3 =0,FR4=FR23LAcosΦ1/h2构件2：∑Fx=0,FR12x=F12cosΦ1∑Fy=0,FR12y=FR32-F12sinΦ1构件1：∑Fx=0,FR41x=FR12x∑Fy=0,FR41y=FR12y∑MA =0,Mb=FR32LABcosΦ1总共有八个方程，八个未知数。

归纳出一元八次方程矩阵：1 0 0 0 0 0 0 0 FR23 Fr-F130 1 -1 0 0 0 0 0 FR4’ 0-LAB COSΦ1/h20 1 0 0 0 0 0 FR40 0 0 1 0 0 0 0 FR12x = F12cosΦ1-1 0 0 0 1 0 0 0 FR12y -F12sinΦ10 0 0 -1 0 1 0 0 FR41x 00 0 0 0 -1 0 1 0 FR41y 0-LABCOSΦ1 0 0 0 0 0 0 1 Mb 0 AX=B进而可得：X=A\B。

虚拟模态综合法matlab虚拟模态分析（Virtual Modal Analysis）是一种结构动力学分析方法，它利用形态传递矩阵和面阵传递矩阵来估计结构的模态参数。

MATLAB作为一款功能强大的数值计算软件，提供了丰富的工具和函数库，可以方便地实现虚拟模态综合法。

本文将介绍如何使用MATLAB进行虚拟模态分析。

一、虚拟模态综合法简介虚拟模态综合法是基于传递矩阵理论的一种模态分析方法。

它通过测量结构的表面加速度响应和表面力响应，利用形态传递矩阵和面阵传递矩阵，估计结构的模态参数。

该方法相比传统的基于模态和频率响应函数的分析方法，具有计算简便、实验要求低等优点。

二、虚拟模态综合法MATLAB实现步骤1. 数据采集首先，需要在结构表面布置加速度传感器和力传感器，采集结构在受到外力激励时的表面加速度响应和表面力响应。

采集的数据可以保存为MATLAB支持的数据格式，如.mat文件。

2. 数据预处理数据采集完成后，需要对采集到的数据进行预处理，主要包括数据去噪、滤波和数据对齐等。

MATLAB提供了丰富的信号处理函数和工具箱，可以方便地进行数据预处理操作。

3. 形态传递矩阵计算形态传递矩阵是虚拟模态综合法的关键步骤，通过计算结构的形态传递矩阵可以得到结构的模态参数。

MATLAB提供了矩阵运算和特征值分解等函数，可以用来计算形态传递矩阵。

4. 面阵传递矩阵计算面阵传递矩阵是虚拟模态综合法的另一个关键步骤，通过计算结构的面阵传递矩阵可以得到结构的模态参数。

MATLAB提供了矩阵运算和特征值分解等函数，可以用来计算面阵传递矩阵。

5. 模态参数估计在得到形态传递矩阵和面阵传递矩阵后，可以通过特征值分解等方法，求解结构的模态参数，包括固有频率和振型。

MATLAB提供了众多的线性代数和特征值分解函数，可以方便地进行模态参数估计。

6. 结果可视化最后，可以使用MATLAB的绘图函数将得到的模态参数进行可视化展示。

可以绘制模态振型、固有频率等图形，直观地显示结构的动态特性。