用“等效法”求重力场、电场叠加区域内几种单摆的周期

“等效单摆”周期的求解“等效单摆”的种类繁多，但由单摆的周期公式可知，一般的等效单摆实质上是改变摆长，或者是改变重力加速度，或者是同时改变摆长和重力加速度的情形。

故等效单摆的周期公式，式中L*为等效摆长， g*为等效（类）重力加速度。

我们要理解摆长L*是从悬点（静止）或系统中的质心（定点）算起；g*为等效（类）重力场中的等效（类）重力加速度，g*的大小和方向是恒定不变的。

一、等效摆长L*：1、单线摆摆长的改变例1、如图所示，长为L的单摆，如果在O点的正下方处的B点固定一个光滑的钉子，使摆球A通过最低点向右摆动，悬线被钉子挡住成为一个新的单摆，则这个单摆的振动周期是多少？（已知摆角θ<50）解：其周期应是摆长为L的单摆的周期T1的一半与摆长为的单摆的周期T2的一半之和。

即2、多线摆（双线摆、三线摆、四线摆等）例2、如图2所示，三线长均为L，BC、BD线拴在天花板上，两线与天花板的夹角均为θ，AB线的下端拴上小球，现使球在垂直于纸面做小角度摆动，问此摆的周期。

解：此摆动方向在前后的竖直平面内，故该摆的等效摆长为OA 的长即：L*=（1+sinθ）L，3、单线连接的两球摆例3、如图3所示，A、B （mA= 3m 、mB=m）两球作长为L的细线相连，A球穿过光滑的水平横杆且可以自由滑动，求此摆的周期？（振幅很小）解：由于两球在摆动过程中沿水平方向所受的外力之和为零，故该系统有一定点O（质点）是不变的，故O点相当于摆的悬点，则求摆长就容易。

由水平方向的动量守恒得：∵mAvA=mBvB∴3mvA=mvBvA、vB分别是两球回到平衡位置时的速率，而周期TA=TB ，即据简谐运动的能量公式有又由上各式得AA或AB为振幅，由三角形相似有故该摆的周期为从种种摆长变化来看，将各种摆等效成一单线摆，确定摆动过程中系统中哪一点是固定的这点就相当于悬点，再确定摆球质心到悬点的距离，便可确定等效摆长，从而确定该摆运动的周期。

用“等效法”求重力场、电场叠加区域内几种单摆的周期一、重力场中单摆的特点1.构成如图1所示，长度为L摆长、不可伸长的轻绳下端悬挂一半径为r小球，且L摆长r，便可构成单摆.2.单摆的受力特点如图2所示，单摆摆动过程中，摆球始终会受竖直向下的重力和沿着细绳方向且指向悬点的拉力FT.3.单摆的周期在单摆的最大偏角θ≤5°的条件下，T=2πLg （其中L 指摆长，g指当地重力加速度）.二、重力场、电场叠加区域内单摆的周期1.电场、重力场的方向相互平行例1如图3所示，一单摆在重力场、匀强电场相互叠加的区域内振动，其最大偏角θ≤5°，单摆的摆长和摆球的质量分别为L和m，悬挂摆球的细线绝缘且质量不计，当地的重力加速度为g，匀强电场的场强大小为E，方向竖直向上，摆球带有正电荷，电荷量为q，且Eq≤mg，试计算此单摆的周期.解析如图4所示，对重力场、匀强电场相互叠加的区域内振动的带电小球进行受力分析，并比较图2中单摆的摆球的受力情况，得图4中的等效重力G等效=mg-Eq.图4中的等效重力加速度g等效=G等效m=mg-Eqm.由单摆的周期公式得图4中的单摆的周期T等效=2πLg等效=2πLg-Eqm.2.电场、重力场的方向相互垂直例2如图5所示，一单摆在重力场、匀强电场相互叠加的区域内振动，其最大偏角θ≤5°，单摆的摆长和摆球的质量分别为L和m，悬挂摆球的细线绝缘且质量不计，当地的重力加速度为g，匀强电场的场强方向水平向右，摆球所受的电场力是重力的43倍，试计算此单摆的周期.解析如图6所示，对重力场、匀强电场相互叠加的区域内振动的带电小球进行受力分析，并比较图2中单摆摆球的受力情况得图6中的等效重力G等效=（mg）2+（Eq）2=53mg.图4中的等效重力加速度g等效=G等效m=53g.由单摆的周期公式得图4中的单摆的周期T等效=2πLg等效=2π3L5g.3.电场、重力场的方向既不平行、也不垂直例3如图7所示，一单摆在重力场、匀强电场相互叠加的区域内振动，其最大偏角θ≤5°，单摆的摆长和摆球的质量分别为L和m，悬挂摆球的细线绝缘且质量不计，当地的重力加速度为g，匀强电场的场强方向与水平向右方向间的夹角为30°，摆球所受的电场力的大小等于重力的大小，试计算此单摆的周期.解析如图8所示，对重力场、匀强电场相互叠加的区域内振动的带电小球进行受力分析，并比较图2中单摆的摆球的受力情况，可得：由平行四边形定则可得，图6中的等效重力G等效=mg，方向与匀强电场方向间的夹角为60°.图4中的等效重力加速度g等效=G等效m.由单摆的周期公式得图4中的单摆的周期T等效=2πLg等效=2πLg.由以上三例不难看出，对于在重力场、电场相互叠加的区域中的各种单摆，只要对摆球进行受力分析，然后利用“等效法”求出重力和电场力的合力，即“等效”重力，进而求出“等效”重力加速度，便可以利用单摆的周期公式轻而易举地求出这种复合场中的单摆周期.可见，“等效法”对于这一类问题具有事半功倍的作用，作为一线的高中物理教师，应有意识地培养学生利用“等效法”解决高中物理问题的能力，以提高他们的思维能力.伏安法测定电源E、r的系统误差分析方法。

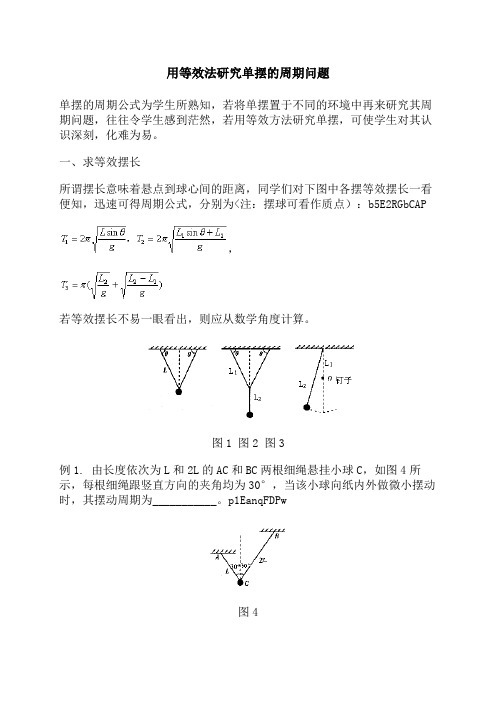
用等效法研究单摆的周期问题单摆的周期公式为学生所熟知，若将单摆置于不同的环境中再来研究其周期问题，往往令学生感到茫然，若用等效方法研究单摆，可使学生对其认识深刻，化难为易。

一、求等效摆长所谓摆长意味着悬点到球心间的距离，同学们对下图中各摆等效摆长一看便知，迅速可得周期公式，分别为<注：摆球可看作质点）：b5E2RGbCAP，若等效摆长不易一眼看出，则应从数学角度计算。

图1 图2 图3例1. 由长度依次为L和2L的AC和BC两根细绳悬挂小球C，如图4所示，每根细绳跟竖直方向的夹角均为30°，当该小球向纸内外做微小摆动时，其摆动周期为___________。

p1EanqFDPw图4简析：本题是一个双线摆问题，解决其周期，首先得确定其等效摆长，连接AB，然后过摆球C作竖直线交直线AB于O点，则OC为该摆的等效摆长，如图5所示，L，故周期：DXDiTa9E3d图5二、求等效重力加速度原始的单摆模型在振动过程中回复力来源于重力的分量，要研究升降机中单摆的周期问题，必须从研究回复力着手，求出其等效重力，再求等效重力加速度g”，则。

RTCrpUDGiT例2. 在升降机中挂着一单摆，摆长为L，当升降机以加速度a匀加速上升的过程中，求单摆的振动周期T。

简析：单摆在摆动过程中，受重力和绳的张力F的作用，当升降机匀加速上升时，单摆一方面绕悬点振动，另一方面沿竖直方向作匀加速直线运动。

5PCzVD7HxA根据力的作用效果，将F分为三个力，如图6所示，在竖直方向上，F3与G的合力产生向上的加速度a，切线方向的F1使单摆返回“平衡”位置，产生切向加速度，F2沿摆线方向产生做圆周运动所需的向心加速度。

jLBHrnAILg图6因为。

又因为F⊥F1，所以：当很小时，。

故单摆在加速上升的升降机中所受回复力与位移成正比，且方向相反，得。

单摆在升降机中摆动周期为：显然，我们称之为等效重力加速度，同理，若升降机以加速度a 匀加速下降，则：。

单摆在重力场中的摆动周期分析引言：单摆是一种简单而古老的物理实验装置，由一个固定在支撑物上的绳或杆与一个悬挂物组成。

它的性质和运动规律一直吸引着科学家和学生们的探索与研究。

本文将对单摆在重力场中的摆动周期进行分析与讨论。

一、背景介绍单摆的运动是受到重力的影响，因此在重力场中摆动的周期非常重要。

周期是指振动往返过程中所需要的时间，也即振动一次所需要的时间。

单摆的周期与摆长、重力加速度以及摆球的质量有关。

二、周期的计算公式单摆的周期可以通过以下公式进行计算：T=2π√(L/g)其中，T表示周期，L表示摆长，g表示重力加速度。

这个公式告诉我们，周期的平方与摆长成正比，与重力加速度的倒数成正比。

三、影响周期的因素3.1 摆长摆长是指摆球离开悬挂点的距离。

通过公式可以看出，摆长越长，周期也就越长。

这是因为摆长增加会使重力对摆球的影响变小。

3.2 重力加速度重力加速度是地球上一个恒定的值，约等于9.8 m/s²。

由公式可以得知，周期与重力加速度的倒数成正比。

也就是说，重力加速度越大，周期越短。

如在月球上，重力加速度较地球小很多，因此单摆的周期会更长。

3.3 摆球质量摆球的质量也会影响周期的长度。

通过公式可以发现，质量的变化不会改变周期的平方根，只会影响周期的比例系数。

换句话说，质量变大或变小，周期的长度会相应变大或变小。

四、实验验证与应用根据以上分析，我们可以利用实验来验证和应用单摆的周期分析。

4.1 实验验证我们可以通过改变摆长、重力加速度或摆球质量来观察周期的变化。

我们可以在同一重力场下，分别选择不同长度的绳子、不同质量的摆球，通过计时来测量不同条件下的周期，从而验证周期与摆长、重力加速度及质量的关系。

4.2 应用领域单摆在实际应用中有一定的价值。

例如，天文学家通过观察天体的周期性运动可以推测星球的质量和距离；物理学家可以通过单摆对物体的质量进行测量。

此外，单摆还被应用于钟表制造和测量重力等领域。

等效单摆及等效周期公式杨绪军单摆是由一根不能伸长的细线，系一个视为质点的摆球构成。

在摆角（新教材）时，摆球的运动可视为简谐振动。

在很多情况下，物体的运动可等效为单摆模型，等效单摆的周期公式可以广义地表示为式中为等效摆长（也称等值摆卡），为等效重力加速度（也称视重加速度）。

1.等效摆长的物理意义及其计算等效摆长等于等效摆球的重心到等效悬点的距离。

例1.试用一只秒表和一颗半径为r的小钢球，设计一种估算凹面镜焦距的方法。

解析：设球面镜的曲率半径为R，对于近轴光线，球面镜的焦距为。

如何确定R呢，可利用等效单摆来测量。

将凹面镜水平放置，让小钢球以最低点为平衡位置做小振幅振动，在不计摩擦的条件下钢球的振动与摆球的振动等效。

因此，钢球可视为等效摆球，凹面镜的曲率中心为等效悬点。

所以等效摆长等于钢球的球心到凹面镜曲率中心的距离，即由此可得等效单摆的周期等于解得因此用秒表测出周期就可估算出焦距。

例2.如图1所示，小球C由细线AC和BC共同挂于重力场中，已知AC=l，BC=2l，且两线与竖直方向的夹角均为。

求小球C在垂直纸面方向上做小振幅振动的周期。

图1解析：小球以AB连线为转轴运动，则重力的作用线与转轴的交点O为等效摆长的固定点，即小球的振动等效于悬线OC所系小球的振动。

取BC的中点D，连接AD，则为等边三角形，，等效摆长为等效摆的周期为2.等效重力加速度的物理意义及计算等效重力加速度的大小等于摆球的视重（摆球相对悬点静止时线的拉力F与摆球的质量m之比），即。

求的基本步骤如下：（1）分析摆球的受力，确定摆球相对静止的位置（即平衡位置）。

（2）计算摆球的视重。

（3）利用，求出视重加速度。

应当注意，在计算拉力时，不能将始终沿悬线方向的力（法线方向）包括在内。

因为只有对回复力有贡献的力，才能改变振动周期。

如图2几种情况，振动周期不变。

图2例3.如图3所示的摆球，由于受到横向风力的作用，偏过角。

若绳长为l，摆球质量为m，且风力稳定，当摆球在纸平面内平衡位置附近振动时，其周期为（）。

等效重力法有妙用求单摆周期显奇能作者：华峰来源：《广东教育·高中》2016年第11期大家都知道，在地球重力场中单摆的振动周期公式是T =2π.可是我们遇到的问题常常是求解单摆在不同条件下的周期，要简捷、顺利地求解此类问题，采用类比的方法，利用等效重力求解有奇效.下面举例分析，希望同学们能够从中受到有益的启示.一、由于重力加速度变化而引起的周期变化【例1】单摆在半径为R1、质量为m1的地球表面的周期为T1，若通过宇宙飞船带到半径为R2的另一颗星球表面时，其周期为T2，试求两种情况下的周期之比.解析：根据万有引力定律有= m′g，再根据单摆周期公式T =2π可得，=.一般来说引起重力加速度变化的原因有：纬度的变化、高度的变化、场环境的变化，为此可将单摆运动知识与万有引力知识、天体运动知识结合起来求解.二、由于摆球受到浮力而引起的周期变化【例2】用一根长为l的细线悬挂一个密度为ρ的小球，并将其放在密度为ρ0（ρ0 < ρ）的液体中，不计液体对小球的运动阻力，试求小球在平衡位置附近做小幅振动的周期.解析：将重力mg = ρgV和浮力F = ρ0gV（V为小球的体积）合成一个等效重力mg′，则有mg′= ρgV- ρ0gV，即g′= （1-）g.由此可得小球的振动周期为T =2π=2π.三、由于单摆处于非惯性系中而引起的周期变化【例3】如图2所示，沿平直轨道以加速度a做匀速直线运动的车厢中，用一根长为l的细线悬挂一质量为m的小球，求小球在平衡位置附近做小幅振动的周期.解析：小球在相对车厢静止时，根据物体受力平衡得到等效重力mg′为mg′=，即mg′=m，则g′=.故此可得小球的振动周期为T=2π=2π.【例4】如图3所示，将一单摆挂于小车上，将小车放于一辆倾角为θ的斜面上，当小车在斜面上加速下滑时，摆线与竖直方向的夹角也为θ.已知摆球直链状为m，摆长为l，重力加速度为g，求此单摆的周期及小车与斜面间的动摩擦因数.解析：由图示可知小车运动过程中，摆线的拉力F = mgcosθ，则g′ = gcosθ，故T =2π.再由受力分析可知，动摩擦因数μ = 0.一般这些阶段的非惯性系系统指处于匀变速直线运动的力学装置，在此前提下就可用类比法快速求解此类问题.四、由于单摆处于匀强电场中而引起周期的变化【例5】将一带电摆球置于一水平向右的匀强电场中，如图4所示.摆球静止时与竖直方向之间的夹角为α，已知摆球质量为m，摆长为l，带电荷量为Q.现若将摆球拉离静止位置一个很小的角度释放，求其振动周期；若要使摆球摆到竖直方向时速度为零，应将摆球拉离竖直方向一个多大的角度？解析：摆球静止在平衡位置时的拉力F=，则g′=，故此摆球的振动周期为T=2π=2π.一般当单摆处于匀强电场中时，由于所受的电场力为恒力，与重力的合力仍为恒力，运用类比法求解简捷、快速.五、单摆周期公式的拓展运用【例6】有一摆钟在地面上走时准确，其标准周期T0 = 2s，现将其移到高山上，发现它一昼夜慢了1min，求此山的高度.已知地面重力加速度g0=9.8m/s2，地球半径R0=6400km.解析：设摆钟在标准时间内的振动次数为N，则其在标准时间内指示的时间t=N·T，在标准时间内慢的时间就应为△t=N·△T，其中N=，△T=T-T0.再由=（），代入已知数据可解得h=4450m.由上述解题过程可归纳出一个有用的结论：钟在标准时间里指示的时间与摆振动的次数成正比，跟钟摆的振动频率成正比.写成比例关系式为：=====.据此可根据题目的特点，达到快速、简捷求解的目的.【例7】竖直放置的光滑圆弧形球面半径R较大，在弧面中心O正上方高h处放置一个小球A，当A自由下落的同时，另一个小球B从球面某处C（OC弧远小于半径R）由静止开始滚下，为时两球相碰，h应满足什么条件？解析：根据题意，小球B在光滑圆弧面上滚动等效于单摆，摆长即为圆弧半径，周期T=2π，考虑到单摆运动的周期性，由相碰的条件有（2n-1）=，解得h=R（n= 1，2，3，…）.一般类单摆模型的计算，主要是求解其等效摆长或等效重力加速度.练习1. 已知北京的重力加速度g1=9.812 m/s2，南京的重力加速度g2=9.795 m/s2，在北京准确的钟摆，如果放在南京，钟将走慢还是走快？一昼夜差多少？要使其走时准确，如何调整摆长？2. 如图5所示，一个质量为2m的球体A套在光滑水平杆上，用一长为l的小球B与A连接，约束A球，将B球拉离竖直方向一个很小的角度，释放B球的同时撤去A球的约束，之后A、B两球都将做简谐运动，试求A球和B球的周期.3. 如图6所示，半径为R=10m的光滑凹球面容器固定在地面上，有一小木块在距容器最低点P=10cm的C点，由静止无摩擦滑下，则小木块自静止滑下到第二次通过P点时所经历的时间为多少？若此装置放在以加速度a向上运动的实验舱里，上述所求的时间又是多少？责任编辑李平安。

用等效法研究类单摆的周期单摆的周期公式为学生所熟知，一些质点的运动类似于单摆做简谐运动，于不同的环境中再来研究其周期问题，往往令学生感到茫然，若用等效方法研究单摆的周期，则可化难为易。

一、用等效模型求类单摆的周期T如图所示，在光滑的圆弧槽底端有一小球，且知圆弧半径R 远大于圆弧长(θ≤5°)，其受力类似于单摆，容易证得小球运动为简谐运动，则其周期为T ＝2πR g。

【典例1】如图9所示，ACB 为光滑弧形槽，弧形槽半径为R ，C 为弧形槽最低点，R ≫»AB .甲球从弧形槽的圆心处自由下落，乙球从A 点由静止释放，问：图9(1)两球第1次到达C 点的时间之比；(2)若在圆弧的最低点C 的正上方h 处由静止释放小球甲，让其自由下落，同时将乙球从圆弧左侧由静止释放，欲使甲、乙两球在圆弧最低点C 处相遇，则甲球下落的高度h 是多少？ 答案 (1)22π (2)2n ＋12π2R8(n ＝0,1,2…)解析 (1)甲球做自由落体运动R ＝12gt 12，所以t 1＝2R g乙球沿圆弧做简谐运动(由于»AC ≪R ，可认为摆角θ＜5°).此运动与一个摆长为R 的单摆运动模型相同，故此等效摆长为R ，因此乙球第1次到达C 处的时间为t 2＝14T ＝14×2πR g ＝π2R g ， 所以t 1∶t 2＝22π. (2)甲球从离弧形槽最低点h 高处自由下落，到达C 点的时间为t 甲＝2hg由于乙球运动存在周期性，所以乙球到达C 点的时间为t 乙＝T 4＋n T 2＝π2Rg(2n ＋1) (n ＝0,1,2，…)由于甲、乙在C点相遇，故t甲＝t乙联立解得h＝2n＋12π2R8(n＝0,1,2…).二、用等效摆长求类单摆的周期1.所谓摆长意味着悬点到球心间的距离，同学们对下图中各摆等效摆长一看便知，迅速可得周期公式，分别为（注：摆球可看作质点）：，图1 图2 图32.若等效摆长不易一眼看出，则应从数学角度计算。