单元数字积分法插补原理
- 格式:ppt
- 大小:1.34 MB
- 文档页数:19

数控原理与系统课程设计课题名称:数字积分插补法直线插补专业:班级:姓名:指导老师:数控原理与系统课程设计任务书班级姓名学号课程设计的目的1)了解连续轨迹控制数控系统的组成原理。
2) 掌握数字积分插补的基本原理。
3)掌握数字积分插补的软件实现方法。
二、课程设计的任务数字积分法又称数字微分分析法DDA(Digital Differential Analyzer)。
数字积分法具有运算速度快、脉冲分配均匀、易于实现多坐标联动及描绘平面各种函数曲线的特点,应用比较广泛。
其缺点是速度调节不便,插补精度需要采取一定措施才能满足要求。
由于计算机有较强的计算功能和灵活性,采用软件插补时,上述缺点易于克服。
本次课程设计具体要求如下:1)数字积分插补法基本原理2)数字积分插补法插补软件流程图3)算法描述(逐点比较法算法在VB中的具体实现)4)编写算法程序清单5)软件运行仿真效果二、课程设计报告要求1)按课程设计任务5点要求为标题,编写课程设计报告,最后加一点:此次课程设计小结(包括设计过程中所碰到的问题、解决办法以及有关设计体会等)。
2)字数在3000字左右。
3)仿真软件一份。
三、学生分组学 生 姓 名数控原理与系统课程设计说明书一、数字积分法直线插补的基本原理数字积分法是利用数字积分的方法,计算刀具沿各坐标轴的位移,使得刀具沿着所加工的轮廓曲线运动利用数字积分原理构成的插补装置称为数字积分器,又称数字微分分析器(Digital Differential Analyzer ),简称DDA 。
数字积分器插补的最大优点在于容易实现多坐标轴的联动插补、能够描述空间直线及平面各种函数曲线等。
因此,数字积分法插补在轮廓数控系统中得到广泛的应用。
从几何角度来看,积分运算就是求出函数Y = f (t )曲线与横轴所围成的面积,从t =t 0到t n 时刻,函数Y= f (t )的积分值可表述为⎰⎰==n n tt t t dt )t (Ydt S 00f如果进一步将t ∈[t 0,t n ]的时间区划分为若干个等间隔Δt 的小区间,当Δt 足够小时,函数Y 的积分可用下式近似表示t Y Ydt S n i i tt n ∆∑⎰-=≈=1在几何上就是用一系列的小矩形面积之和来近似表示函数f (t )以下的积分面积。



主讲人:罗福源原理利用数字积分的原理,计算各坐标轴的位移,形成插补轨迹。
在计算机里,积分即是求和,也就是累加。
那么加数是什么?是微位移(Δx、Δy、......),因此数字积分法又称为DDA法,(Digital Differential Analyzer),即数字微分分析器法。
特点允许多个坐标轴同时输出脉冲。
优点运算速度快、脉冲分配均匀,易于实现多坐标联动。
X Δx01234取微位移Δx(<1个脉冲当量)进行累加运算。
随着累加次数逐渐增加,对应动点的x坐标也不断增大。
当完成若干次累加后,位移之和已经超出1个脉冲当量。
此时,利用这个溢出信号让数控系统向x坐标轴发出一个控制脉冲,使之产生一个脉冲当量的位移。
如此不断累加,每当位移之和超出1个脉冲当量,就向x 坐标轴发出一个控制脉冲,直至到达终点,插补结束。
保证Δx 与Δy 符合斜率关系即可:DDA法直线插补e ex y x y =∆∆⎪⎪⎩⎪⎪⎨⎧<=∆<=∆11m y y m x x e e设经累加m 次到达终点,则若取m =2n ,(n 为累加器位数),则易于计算机实现。
因为Δx=x e •2-n 与x e 相比,只是小数点位置不同,不影响累加运算后的有效数位与溢出的判别。
这样,把对Δx 、Δy的累加转变为对x e 与y e 的累加。
Y XA(x e ,y e )Δx2ΔxΔy 2Δy OX -Y平面第一象限直线DDA插补器的示意图:Δt Y轴溢出脉冲X轴溢出脉冲+Y 积分累加器J RYX积分累加器J RX被积函数寄存器J VX (x e )+控制脉冲被积函数寄存器J VY (y e )其它象限的直线DDA插补,参照前述逐点比较法,对终点坐标进行取绝对值并按实际方向进给即可。
累加次数m JVX(存xe)JRX(∑xe)△x JVY(存ye)JRY(∑ye)△y0100000011000 11000001100 20000111000 31000000101 40000110000 51000011100 60000101001 71000010100 80000100001 91000001100 100000111000 111000000101 120000110000 131000011100 140000101001 151000010000 160000100001A (8,6)插补轨迹理想轨迹8756123456O1234YX以第一象限逆圆弧为例V yV x VARYOXP (x i ,y j )B (x e ,y e )DDA法圆弧插补222x y R+=等式两边同时对时间参数t 求导,可得220dx dy x dy dxx y dt dt dt dty+=⇒=-由此可导出第一象限逆圆弧加工时动点沿坐标轴方向的速度分量为=x j y i dx V ky ky dt dy V kx kx dt ⎧==--⎪⎪⎨⎪===⎪⎩在一个单位时间Δt 内,X 和Y 方向上的移动距离微小增量Δ x 、Δ y 为:⎪⎩⎪⎨⎧∆=∆=∆∆=∆=∆tkx t V y t ky t V x i y j x -⎪⎩⎪⎨⎧=∆=∆=∆=∆n --n22--i i j j x t kx y y t ky x 令Δt =1,取k=2-n ,得:插补时寄存的是动点坐标x i 或y j ,是变量。

dda数字积分插补算法DDA(Digital Differential Analyzer)数字积分插补算法是计算机图形学中常用的一种直线段插值算法。
它的主要作用是根据给定的两个端点坐标,通过在直线上等间距采样的方式,计算出直线上各个点的坐标值,从而实现直线的平滑插值。
DDA算法的基本思想是利用直线的斜率来逐步逼近直线的路径,从而计算出直线上各个点的坐标。
具体步骤如下:1. 计算出直线的斜率k,即直线在x轴上的单位增量Δx与在y轴上的单位增量Δy的比例:k = Δy / Δx。
2. 选择直线上两个端点中x值较小的一个作为起始点,并以其坐标值(x0,y0)作为起始值。
3. 将起始点的坐标值作为当前点的坐标值,并将其绘制到屏幕上。
4. 通过递增x坐标值的方式,计算出下一个点的y坐标值,即y = y0 + k。
5. 将下一个点的坐标值(x0+1,y)作为当前点的坐标值,并将其绘制到屏幕上。
6. 重复步骤4和步骤5,直到达到直线的结束点。
通过以上步骤,可以得到直线上各个点的坐标值,从而实现直线的平滑插值。
DDA算法的优点是计算简单、速度快,适用于直线斜率变化不大的情况。
但由于采用等间距采样的方式,可能导致插值结果与实际直线存在误差。
为了更好地理解DDA算法的原理,下面以一个具体的例子来说明。
假设有两个端点坐标分别为(2,2)和(8,5),我们来计算出直线上各个点的坐标。
计算出直线的斜率k = (5-2) / (8-2) = 3/6 = 1/2。
然后,选择起始点(2,2)作为起始值,并将其绘制到屏幕上。
接下来,通过递增x坐标值的方式,依次计算出下一个点的y坐标值。
根据步骤4,我们可以得到以下结果:x | y--------2 | 23 | 2 + 1/2 = 2.54 | 2.5 + 1/2 = 35 | 3 + 1/2 = 3.56 | 3.5 + 1/2 = 47 | 4 + 1/2 = 4.58 | 4.5 + 1/2 = 5我们得到直线上各个点的坐标值为(2,2)、(3,2.5)、(4,3)、(5,3.5)、(6,4)、(7,4.5)和(8,5)。
第三节 数字积分法插补一、数字积分法的基本原理数字积分法又称数字微分分析法(Digital Differential Analyzer )。
这种插补方法可以实现一次、二次、甚至高次曲线的插补,也可以实现多坐标联动控制。
只要输入不多的几个数据,就能加工出圆弧等形状较为复杂的轮廓曲线。
作直线插补时,脉冲分配也较均匀。
从几何概念上来说,函数)(t f y =的积分运算就是求函数曲线所包围的面积S (图3-10所示)。
图3-10 函数)(t f y =的积分S=⎰tydt 0(3-9)此面积可以看作是许多长方形小面积之和,长方形的宽为自变量t ∆,高为纵坐标i y 。
则 S=⎰tydt 0=t y ni i ∆∑=0(3-10)这种近似积分法称为矩形积分法,该公式又称为矩形公式。
数学运算时,如果取t ∆=1,即一个脉冲当量,可以简化为:S=∑=ni iy(3-11)由此,函数的积分运算变成了变量求和运算。
如果所选取的脉冲当量足够小,则用求和运算来代替积分运算所引起的误差一般不会超过容许的数值。
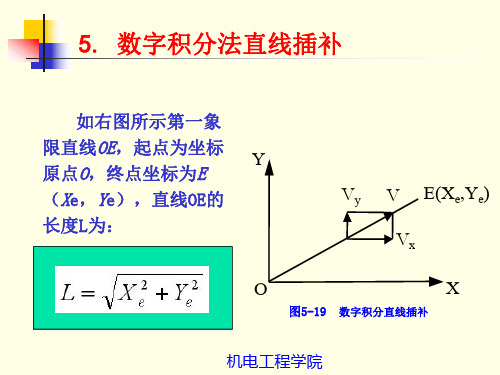
二、DDA 直线插补 1.DDA 直线插补原理图3-11 直线插补设xy 平面内直线OA ,起点(0,0),终点为(e x ,e y ),如图3-11所示。
若以匀速V 沿OA 位移,则V 可分为动点在x 轴和y 轴方向的两个速度x V 、y V ,根据前述积分原理计算公式,在x 轴和y 轴方向上微小位移增量x ∆、y ∆应为⎩⎨⎧∆=∆∆=∆t V y tV x y x (3-12) 对于直线函数来说,x V 、y V ,V 和L 满足下式⎪⎪⎩⎪⎪⎨⎧==L y VV Lx V V e y e x 从而有⎩⎨⎧==e yex ky V kx V (3-13) 其中:LVk =因此坐标轴的位移增量为⎩⎨⎧∆=∆∆=∆tky y tkx x e e (3-14) 各坐标轴的位移量为⎪⎪⎩⎪⎪⎨⎧∆==∆==⎰∑⎰∑==tn i e e t n i e e ty k dt ky y t x k dt kx x 0101(3-15) 所以,动点从原点走向终点的过程,可以看作是各坐标轴每经过一个单位时间间隔t ∆,分别以增量e kx 、e ky 同时累加的过程。