
组合变形
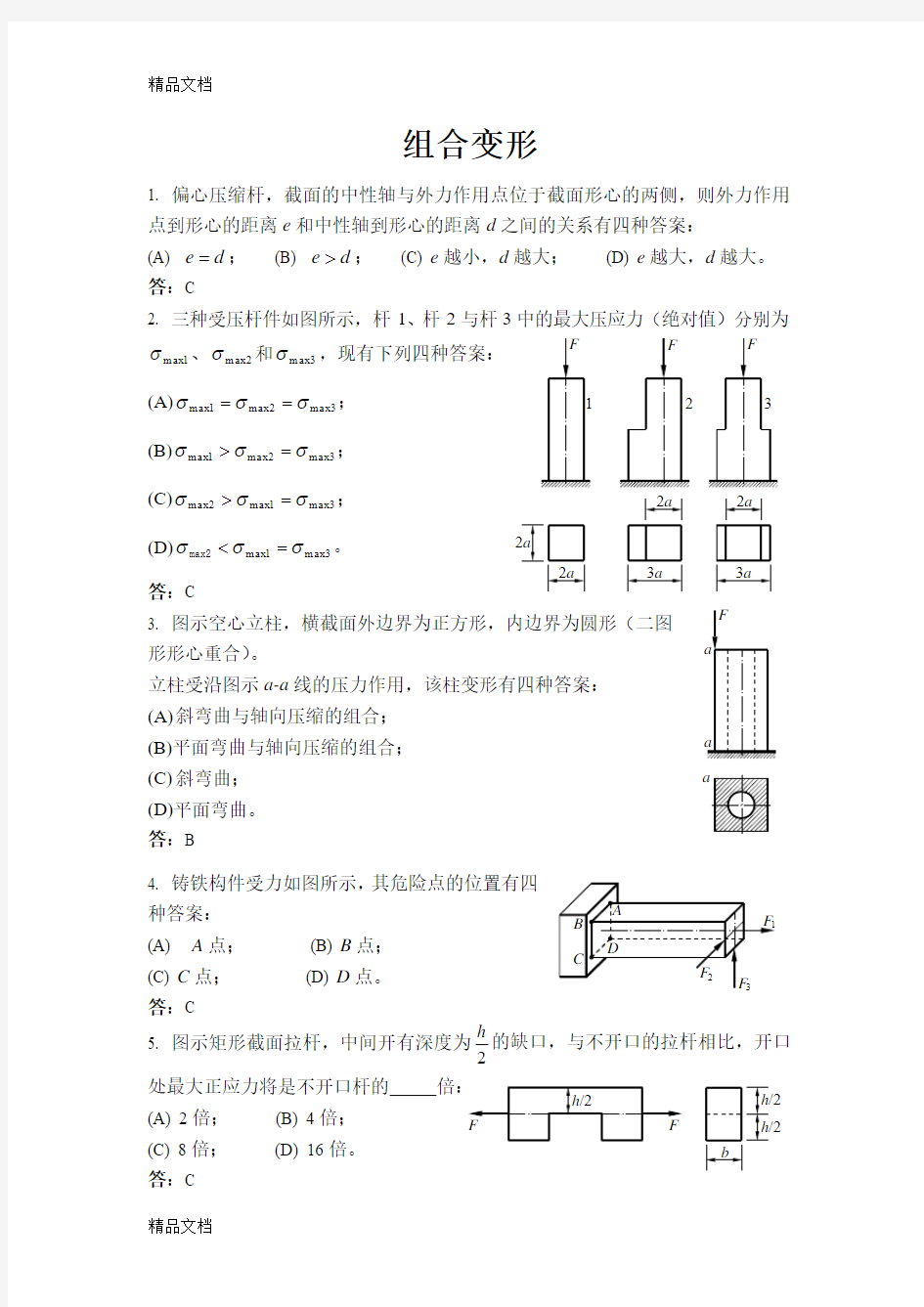
1. 偏心压缩杆,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点到形心的距离e 和中性轴到形心的距离d 之间的关系有四种答案: (A) d e =; (B) d e >; (C) e 越小,d 越大; (D) e 越大,d 越大。 答:C
2. 三种受压杆件如图所示,杆1、杆2与杆3中的最大压应力(绝对值)分别为
1m ax σ、2m ax σ和3m ax σ,现有下列四种答案: (A)3max 2max 1max σσσ==; (B)3max 2max 1max σσσ=>; (C)3max 1max 2max σσσ=>; (D)3max 1max σσσ= 3. 形形心重合)。 立柱受沿图示 a-a (A) 斜弯曲与轴向压缩的组合; (B)平面弯曲与轴向压缩的组合; (C) 斜弯曲; (D)平面弯曲。 答:B 4. 铸铁构件受力如图所示,种答案: (A) A 点; (B) B 点; (C) C 点; (D) D 点。 答:C 5. 图示矩形截面拉杆,中间开有深度为 2 h 的缺口,与不开口的拉杆相比,开口处最大正应力将是不开口杆的 倍:(A) 2倍; (B) 4倍; (C) 8倍; (D) 16倍。 答:C 6. 三种受压杆件如图所示,杆1、杆2与杆3中的最大压应力(绝对值)分别为 1m ax σ、2m ax σ和3m ax σ (A)max3 2max 1max σσσ<<; (B)3max 2max max1σσσ=<; (C)2max max3max1σσσ<<; (D)2max 3max 1max σσσ<=。 答:C 7. 正方形等截面立柱,受纵向压力F 作用。当力F 作用点由A 移至B 时,柱内最大压应力的比值max max B A σσ有四种答案: (A) 1:2; (B) 2:5; (C) 4:7; (D) 5:2。 答:C 8. 图示矩形截面偏心受压杆,其变形有下列四种答案: (A) 轴向压缩和平面弯曲的组合; (B)轴向压缩、平面弯曲和扭转的组合; (C)缩和斜弯曲的组合; (D)轴向压缩、斜弯曲和扭转的组合。 答:C 9. 矩形截面梁的高度mm 100=h ,跨度m 1=l 。梁中点承受集中力F ,两端受力 kN 301=F ,三力均作用在纵向对称面内,mm 40=a 。若跨中横截面的最大正 应力与最小正应力之比为3 5 。试求F 解:偏心距 mm 102 =-=a h e 跨中截面轴力 1N F F = 跨中截面弯矩e F Fl M 1max 4-= (正弯矩) ,或 4 1m a x Fl e F M -=(负弯矩) 则 356464211 2 11 min max =---+=bh e F Fl bh F bh e F Fl bh F σσ,得kN 7.1=F 或 356 464211 211 min max =- -- +=bh Fl e F bh F bh Fl e F bh F σσ,得kN 7.0=F 12. 图示混凝土坝,坝高m 2=l ,在混凝土坝的右侧整个面积上作用着静水压力,水的质量密度331kg/m 10=ρ,混凝土的质量密度332kg/m 102.2?=ρ。试求坝解由 13. 解14. 答 15. 16. p 20. 图示水平直角折杆受铅直力F 作用。圆轴AB 的直径mm 100=d , mm 400=a ,GPa 200=E ,25.0=ν。在截面D 顶点K 处,测得轴向线应变 401075.2-?=ε。试求该折杆危险点的相当应力3r σ。 解 又=σσ21. ][=σ解 σ22. 1=z F 解T 由4r σ23. ][=σ解由3r σ 24. 解由 w C 得 F C 25. 102=F 解M =T 由4r σ= 26. 6=F 拉应力[(1)(2)(3)解:(1)(2)(3)= σ= τ1σt 11r σ 27. 悬臂梁AB 的横截面为等边三角形,形心在C 点,承受均布载荷q ,其作用方向及位置如图所示,该梁的变形有四种答案: (A)平面弯曲; (B)斜弯曲; (C)纯弯曲; (D)弯扭组合。 答:A 28. 开口薄壁管一端固定一端自由,自由端受集中力F 梁的横截面和力F 的作用线如图所示,C 为横截面形心,该梁的变形有四种答案: (A)平面弯曲; (B)斜弯曲; (C)平面弯曲+扭转; (D)斜弯曲+扭转。 答:D 29. 悬臂梁的自由端受垂直于梁轴线的力F 作用,力作用方向与梁横截面形状分别如图所示,则 图(a)的变形为___________________; 图(b)的变形为___________________; 图(c)的变形为___________________。 答:斜弯曲;平面弯曲;斜弯曲+扭转 30. 按照第三强度理论,图示杆的强度条件表达式有四种答案: (A) ][)(4)(2p 2σ≤++W T W M A F z ; (B)][p σ≤++ W T W M A F z ; (C)][)()( 2p 2σ≤++W T W M A F z ; (D)][)(4)(2p 2σ≤++W T W M A F z 。 答:D 31. 图示水平的直角刚架ABC ,各杆横截面直径均为cm 6=d ,cm 40=l , cm 30=a ,自由端受三个分别平行于x 的力作用,材料的许用应力120][=σ第三强度理论确定许用载荷[F ]。 解:截面A 处, F F 3N =, F T 6.0=, M 由][42 23r στσσ≤+=x x ,得17.2≤F (c) (b) 正方形(a) x 截面由σ则32. 解: 33. 34. 图示圆杆的直径mm 200=d ,两端承 MPa 102003?=E ,3.0=ν,MPa 170][=σ445103-?= ε解:杆表面点K 处 MPa 20π42 ==d F x σ 利用斜截面的应力公式与广义胡克定律得 ν εσντ+--= 12/)1(45 E x x 则][MPa 4.913224r στσσ<=+=,满足强度条件。 35. 图示圆截面钢杆的直径mm 20=d ,承受轴向力F ,力偶m N 801e ?=M , m N 1002e ?=M ,MPa 170][=σ。试用第四强度理论确定许用力[F ] 。 解:横截面外圆周上的点 31 e 2π32π4d M d F += σ,3 2e π16d M =τ。 由][3224r στσσ≤+=,得kN 6.8=F 。 36. 图示圆杆的直径mm 100=d ,长度m 1=l 2F 、3F ,kN 1201=F ,kN 502=F ,603=F 度理论校核杆的强度。 解:危险截面在固定端处 22321]2)([)2( l F F d F M -+=,2 3d F T = MPa 1341=+= z W M A F σ,3.15p ==W T τ则][MPa 4.1374223r στσσ<=+= 37. 梁的斜弯曲是两个互相垂直平面内最主要的特点是______________________________。 答:平面弯曲;挠曲面与弯矩作用面不重合 38. 矩形截面梁产生斜弯曲,某横截面尺寸与弯矩矢量方向如图所示,则中性轴与z 轴所成的角度为________________。 答:?=87.828arctan 39. 边长为a 的正方形截面梁产生拉弯组合变形,内力关系为12 N a F M M z y = =,则中性轴与z 轴所成的角度为_______,截面形心到中性轴的距离为_______。 答:45°; 2 a 40. 画出图示空心截面的截面核心的大致形状。 答: 41. 画出图示正六边形截面的截面核心的大致形状。 答: 42. 画出图示T 形截面的截面核心的大致形状。 答: 43. 边长为a 的正方形截面,其截面核心的边界为______________形,顶点到正方形形心的距离为________________。 答:正方;6 a 44. 图示截面外边界为矩形,内边界为边长a 的正方形,其截面核心的边界为_______形,在z 轴上的截距为_______。 答:菱;a 60 23 45. 等边三角形截面的截面核心的边界为_______________形,核心边界的某个顶点和三角形截面形心的连线与该顶点对应的中性轴所成的角度为__________。 答:等边三角;90° 46. 圆截面杆受弯矩M 与扭矩T 作用产生弯扭组合变形,T M =。横截面上全应力值相等的点位于______________线上。 答:椭圆 47. 圆截面杆受弯矩M 与扭矩T 作用产生弯扭组合变形,T M =。按最大切应力强度理论,横截面上相当应力值相等的点位于______________线上。 答:椭圆 48. 矩形截面直杆发生扭转与弯曲组合变形,按照最大切应力强度理论,横截面上角点的相当应力有四种答案: (A)σσ=3r ; (B)τσ23r =; (C)223r τσσ+=; (D)223r 3τσσ+=。 (σ、τ分别表示该点处非零的正应力与切应力大小) 答:A 49. 圆截面直杆,轴向拉伸时轴线的伸长量为1ΔL ,偏心拉伸时轴线的伸长量为 2ΔL ,设两种情况的作用力相同,两个伸长量的关系有四种答案: (A)21ΔΔL L >; (B)21ΔΔL L <; (C)21ΔΔL L =; (D)不确定。 答:C 50. 偏心拉伸直杆中的最大拉应力必大于最大压应力。该论断正确与否?( ) 答:非 第八章组合变形构件的强度习题 一、填空题 1、两种或两种以上基本变形同时发生在一个杆上的变形,称为()变形。 二、计算题 1、如图所示的手摇绞车,最大起重量Q=788N,卷筒直径D=36cm,两轴承间的距离l=80cm,轴的许用应力[]σ=80Mpa。试按第三强度理论设计轴的直径d。 2、图示手摇铰车的最大起重量P=1kN,材料为Q235钢,[σ]=80 MPa。试按第三强度理论选择铰车的轴的直径。 3、图示传动轴AB由电动机带动,轴长L=1.2m,在跨中安装一胶带轮,重G=5kN,半径R=0.6m,胶带紧边张力F1=6kN,松边张力F2=3kN。轴直径d=0.1m,材料许用应力[σ]=50MPa。试按第三强度理论校核轴的强度。 4、如图所示,轴上安装有两个轮子,两轮上分别作用有F=3kN及重物Q,该轴处于 平衡状态。若[σ]=80MPa。试按第四强度理论选定轴的直径d。 5、图示钢质拐轴,AB轴的长度l AB=150mm, BC轴长度l BC=140mm,承受集中载荷F 的作用,许用应力[σ]=160Mpa,若AB轴的抗弯截面系数W z=3000mm3,。试利用第三强度理论,按AB轴的强度条件确定此结构的许可载荷F。(注:写出解题过程) 6、如图所示,由电动机带动的轴上,装有一直径D=1m的皮带轮,皮带紧边张力为2F=5KN,松边张力为F=2.5KN,轮重F P=2KN,已知材料的许用应力[σ]=80Mpa,试按第三强度理论设计轴的直径d。 7、如图所示,有一圆杆AB长为l,横截面直径为d,杆的一端固定,一端自由,在自由端B处固结一圆轮,轮的半径为R,并于轮缘处作用一集中的切向力P。试按第三强度理论建立该圆杆的强度条件。圆杆材料的许用应力为[σ]。 组合变形练习题 一、选择 1、应用叠加原理的前提条件是:。 A:线弹性构件; B:小变形杆件; C:线弹性、小变形杆件; D:线弹性、小变形、直杆; 2、平板上边切h/5,在下边对应切去h/5,平板的强度。 A:降低一半; B:降低不到一半; C:不变; D:提高了; 3、AB杆的A处靠在光滑的墙上,B端铰支,在自重作用下发生变形, AB杆发生变形。 A:平面弯曲 B:斜弯; C:拉弯组合; D:压弯组合; 4、简支梁受力如图:梁上。 A:AC段发生弯曲变形、CB段发生拉弯组合变 形 B:AC段发生压弯组合变形、CB段发生弯曲变形 C:两段只发生弯曲变 形 D:AC段发生压弯组合、CB段发生拉弯组合变形 5、图示中铸铁制成的压力机立柱的截面中,最合理的是。 6、矩形截面悬臂梁受力如图,P2作用在梁的中间截面处,悬臂梁根部截面上的最大应力为:。 A:σ max =(M y 2+M z 2)1/2/W B:σ max =M y /W y +M Z /W Z C:σ max =P 1 /A+P 2 /A D:σ max =P 1 /W y +P 2 /W z 7、塑性材料制成的圆截面杆件上承受轴向拉力、弯矩和扭矩的联合作用,其强度条件是。 A:σ r3 =N/A+M/W≤|σ| B:σ r3 =N/A+(M2+T2)1/2/W≤|σ| C:σ r3 =[(N/A+M/W)2+(T/W)2]1/2≤|σ| D:σ r3 =[(N/A)2+(M/W)2+(T/W)2]1/2≤|σ| 8、方形截面等直杆,抗弯模量为W,承受弯矩M,扭矩T,A点处正应力为σ,剪应力为τ,材料为普通碳钢,其强度条件为:。 A:σ≤|σ|,τ≤|τ| ; B: (M2+T2)1/2/W≤|σ| ; C:(M2+0.75T2)1/2/W≤|σ|; D:(σ2+4τ2)1/2≤|σ| ; 9、圆轴受力如图。该轴的变形为: A:AC段发生扭转变形,CB段发生弯曲变形 B:AC段发生扭转变形,CB段发生弯扭组合变形 C:AC段发生弯扭组合变形,CB段发生弯曲变形 10组合变形 图10.4 斜弯曲分析参考图 10 组合变形 10.1 组合变形的概念和实例 分析组合变形问题时,通常是先把作用在杆件上的载荷向杆件的轴线简化,即把构件上的外力转化成几组静力等效的载荷,其中每一组载荷对应着一种基本变形。 工程中,常见的组合变形主要有斜弯曲、拉伸(压缩)与弯曲的组合、弯曲与扭转的组合。下面讨论这三种组合变形的强度计算问题。 10.2 斜弯曲 10.2.1 斜弯曲时横截面上的应力 外力简化 ? ?sin ,cos z y P P P P == 内力: ? ?cos )(cos )(y z M x l P x l P M =-=-= ? ?sin )(sin )(z y M x l P x l P M =-=-= 式中)(x l P M -=是集中力P 在横截面m-n 上所引起的弯矩,在计算中可取绝对值。 应力: 任意截面m-n 上任意点C (y ,z )处的应力可采用叠加法计算。在xy 平面内的平面 弯曲(由于z M 的作用)产生的正应力为 y I M I y M z z z cos ? σ== ' 由于在xz 平面内的平面弯曲(由于y M 的作用) 产生的正应力为 图10.1起重机构ACB 梁受力分析 图10.2传动轴受力分析 z I M I z M y y y sin ? = = σ'' C 点处的正应力,即 y y z z I z M I y M += ''+'=σσσ???? ??+=z I y I M y z sin cos ?? (10.1) 10.2.2 斜弯曲时的强度计算 强度条件为 max 11z y cos sin M y z I I ??σ?? =+≤ ? ???[]σ (10.2) 对于有棱角的矩形截面,根据图10.4所示的应力分布,公式(10.2)还可写成 ≤ + = z zmax y y max max W M W M σ[]σ (10.3) 若材料的抗拉强度和抗压强度不同,则应分别对1D 点和2D 点都进行强度计 算。 0 sin cos 0y 0z =???? ??+=z I y I M ??σ 因为0≠M ,所以有 0sin cos 0y 0z =+z I y I ? ? (10.4) 此即斜弯曲时的中性轴方程。设中性轴与z 轴的夹角为α,根据公式(10.4)有 ? αtg tan y z 00I I z y -== (10.5) 由式(10.5)可得出以下两点结论: (1) 对于z y I I ≠的截面,则?α≠。这表明此种梁在发生斜弯曲时,其中性轴与外力P 所在的纵向平面不垂直(图10.5b )。 (2) 对于圆形、正方形及其他正多边形截面,由于z y I I =,故可由式(10.5)得:?α-=,这说明中性轴总是与载荷所在的纵向面垂直,即此类截面的梁不会产生斜弯曲。 10.2.3 斜弯曲的变形计算 3 3 y y z z cos 33P l P l f EI EI ?==-- 3 3z z y y cos 33Pl P l f EI EI ?==-- 2 z 2y f f f += (10.6) 设总挠度f 与y 轴的夹角为β(图10.6b ), 则有 ? βtg tan y z y z I I f f == (10.7) 关于挠度、中性轴及外力P 的位置之间的关系,现作进一步讨论: 图10.6斜弯图 第八章 组合变形及连接部分的计算 习题解 [习题8-1] 14号工字钢悬臂梁受力情况如图所示。已知m l 8.0=,kN F 5.21=, kN F 0.12=,试求危险截面上的最大正应力。 解:危险截面在固定端,拉断的危险点在前上角点,压断的危险点在后下角,因钢材的拉压 性能相同,故只计算最大拉应力: 式中,z W ,y W 由14号工字钢,查型钢表得到3 102cm W z =,3 1.16cm W y =。故 MPa Pa m m N m m N 1.79101.79101.168.0100.11010228.0105.2363 63363max =?=???+?????=--σ [习题8-2] 受集度为 q 的均布荷载作用的矩形截面简支梁,其荷载作用面与梁的纵向对称面间的夹角为 030=α,如图所示。已知该梁材料的弹性模量 GPa E 10=;梁的尺寸为 m l 4=,mm h 160=,mm b 120=;许用应力MPa 12][=σ;许用挠度150/][l w =。试校核梁的强度和刚度。 解:(1)强度校核 )/(732.1866.0230cos 0m kN q q y =?== (正y 方向↓) )/(15.0230sin 0m kN q q z =?== (负z 方向←) )(464.34732.181 8122m kN l q M y zmaz ?=??== 出现在跨中截面 )(24181 8122m kN l q M z ymaz ?=??== 出现在跨中截面 )(51200016012061 61322mm bh W z =??== )(3840001201606 1 61322mm hb W y =??== 最大拉应力出现在左下角点上: y y z z W M W M max max max + = σ MPa mm mm N mm mm N 974.1138400010251200010464.33 636max =??+??=σ 因为 MPa 974.11max =σ,MPa 12][=σ,即:][max σσ< 所以 满足正应力强度条件,即不会拉断或压断,亦即强度上是安全的。 (2)刚度校核 = 组合变形 基 本 概 念 题 一、选择题 1. 偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点到 形心的距离e 和中性轴到形心距离d 之间的关系是( )。 A .e = d B .e >d C .e 越小,d 越大 D .e 越大,d 越小 2.三种受压杆件如图所示,设 杆1、杆2和杆3中的最大压应力(绝 对值)分别用1max σ、2max σ、 3max σ表示,则( )。 A .1max σ=2max σ=3max σ B .1max σ>2max σ=3max σ C .2max σ>1max σ=3max σ D .2max σ<1max σ=3max σ 题2图 3.在图示杆件中,最大压应力发生在截面上的( )。 A .A 点 B .B 点 C .C 点 D .D 点 题3图 题4图 4. 铸铁杆件受力如图4所示,危险点的位置是( )。 A .①点 B .②点 C .⑧点 D .④点 5. 图示正方形截面直柱,受纵向力P 的压缩作用。则当P 力作用点由A 点移至B 点时柱内最大压应力的比值()max A σ﹕()max B σ为( )。 A .1﹕2 B .2﹕5 C .4﹕7 D .5﹕2 6. 图示矩形截面偏心受压杆件发生的变形为( )。 A .轴向压缩和平面弯曲组合 B .轴向压缩,平面弯曲和扭转组合 C .轴向压缩,斜弯曲和扭转组合 D .轴向压缩和斜弯曲组合 -41- 题5图 题6图 7. 图所示悬臂梁的横截面为等边角钢,外力P 垂直于梁轴,其作用线与形心轴 y 垂直,那么该梁所发生的变形是( )。 A .平面弯曲 B .扭转和斜弯曲 C .斜弯曲 D .两个相互垂直平面(xoy 平面和xoz 平面)内的平面弯曲 题7图 8. 图示正方形截面杆受弯扭组合变形,在进行强度计算时,其任一截面的危 险点位置有四种答案,正确的是( )。 A .截面形心 B .竖边中点A 点 C .横边中点B 点 D .横截面的角点D 点 题8图 题9图 9. 图示正方形截面钢杆,受弯扭组合作用,若已知危险截面上弯矩为M ,扭 矩为T ,截面上A 点具有最大弯曲正应力σ和最大剪应力τ,其抗弯截面模量为W 。关于A 点的强度条件是( )。 A .σ≤[σ],τ≤[τ] B .W T M 2122)(+≤[σ] C .W T M 2122)75.0(+≤[σ] D .2122)3(τσ+≤[σ] 10. 折杆危险截面上危险点的应力状态是图中的( )。 -42- - 1 - 第八章组合变形构件的强度习题答案 一、填空题 1、组合 二、计算题 1、解:317888010157.610(N m m 4M =???=??3 36 78810141.8410(N m m 2 T =? ?=?? 3 3 80 0.10.1r d d σ = = ≤ 解得 d ≥30mm 2 、解:(1 轴的计算简图 画出铰车梁的内力图: 险截面在梁中间截面左侧, P T P M 18. 02. 0max == (2 强度计算第三强度理论:( ([]σπσ ≤+= += 2 2 3 2 2 3 18. 02. 032 P P d W T M Z r [] ( ( ( ( mm m d 5. 320325. 010 118. 01012. 010 8032 10 118. 01012. 032 3 2 3 2 3 6 3 2 3 2 3 ==??+????= ??+??≥ πσπ 所以绞车的轴的最小直径为32.5mm 。 3、解: - 2 - m kN 8. 1? m kN 2. 4? (1)外力分析,将作用在胶带轮上的胶带拉力F 1、F 2向轴线简化,结果如图b .传动轴受竖向主动力: kN 1436521=++=++=F F G F ,此力使轴在竖向平面内弯曲。附加力偶为: ((m kN 8. 16. 03621?=?-=-=R F F M e ,此外力偶使轴发生变形。 故此轴属于弯扭组合变形。(2)内力分析 分别画出轴的扭矩图和弯矩图如图(c )、(d )危险截面上的弯矩m kN 2. 4?=M ,扭矩m kN 8. 1?=T (3)强度校核 组合变形 1. 偏心压缩杆,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点到形心的距离e 和中性轴到形心的距离d 之间的关系有四种答案: (A) e d =; (B) e d >; (C) e 越小,d 越大; (D) e 越大,d 越大。 答:C 2. 三种受压杆件如图所示,杆1、杆2与杆3中的最大压应力(绝对值)分别为max1σ、max 2σ和 max 3σ,现有下列四种答案: (A)max1max 2max 3σσσ==; (B)max1max 2max 3σσσ>=; (C)max 2max1max 3σσσ>=; (D)max1max3σσσ<=max2。 答:C 3. 重合)。立柱受沿图示a-a (A)斜弯曲与轴向压缩的组合; (B)平面弯曲与轴向压缩的组合; (C)斜弯曲; (D)平面弯曲。 答:B 4. (A) A 点; (B) B 点; (C) C 点; (D) D 点。 答:C 5. 图示矩形截面拉杆,中间开有深度为/2h 的缺口,与不开口的拉杆相比,开口处最大正应力将是不开口杆的 倍: (A) 2倍; (B) 4倍; (C) 8倍; (D) 16倍。 答:C 6. 三种受压杆件如图所示,杆1、杆2与杆3中的最大压应力(绝对值)分别为max1σ、max 2σ和max 3σ,现有下列四种答案: (A)max1max 2max3σσσ<<; (B)max1max 2max3σσσ<=; (C)max1max3max 2σσσ<<; (D)max1max 3max 2σσσ=<。 答:C 7. 正方形等截面立柱,受纵向压力F 移至B 时,柱内最大压应力的比值max max A B σ σ(A) 1:2; (B) 2:5; (C) 4:7; (D) 5:2。 答:C 8. 图示矩形截面偏心受压杆,其变形有下列四种答案:(A)轴向压缩和平面弯曲的组合; (B)轴向压缩、平面弯曲和扭转的组合; (C)缩和斜弯曲的组合; (D)轴向压缩、斜弯曲和扭转的组合。 答:C 9. 矩形截面梁的高度100mm h =,跨度1m l =。梁中点承受集中力F ,两端受力130kN F =,三力均作用在纵向对称面内,40mm a =。若跨中横截面的最大正应力与最 小正应力之比为5/3。试求F 值。 解:偏心距10mm 2 h e a =-= 跨中截面轴力 N 1F F = 跨中截面弯矩max 14Fl M Fe = -(正弯矩),或 max 14 Fl M Fe =- (负弯矩) 组合变形 1试分别求出图示不等截面杆的绝对值最大的正应力,并作比较。 解题思路: (1)图(a )下部属偏心压缩,按式(12-5)计算其绝对值最大的正应力,要正确计算式中 的弯曲截面系数; (2)图(b )是轴向压缩,按式(8-1)计算其最大正应力值; (3)图(a )中部属偏心压缩,按式(12-5)计算其绝对值最大的正应力,要正确计算式中 的弯曲截面系数。 答案:2a 34)(a F =σ,2 b )(a F =σ,2 c 8)(a F =σ 2某厂房一矩形截面的柱子受轴向压力1F 和偏心荷载2F 作用。已知kN 1001=F , kN 452=F ,偏心距mm 200=e ,截面尺寸mm 300,mm 180==h b 。 (1)求柱内的最大拉、压应力;(2)如要求截面内不出现拉应力,且截面尺寸b 保持不变,此时h 应为多少?柱内的最大压应力为多大? 解题思路: (1)立柱发生偏心压缩变形(压弯组合变形); (2)计算立柱I-I 截面上的内力(轴力和弯矩); (3)按式(12-5)计算立柱截面上的最大拉应力和最大压应力,要正确计算式中的弯曲截 面系数; (4)将b 视为未知数,令立柱截面上的最大拉应力等于零,求解b 并计算此时的最大压应 力。 答案:(1)MPa 648.0max t =σ,MPa 018.6max c =σ (2)cm 2.37=h ,MPa 33.4max c =σ 3旋转式起重机由工字钢梁AB 及拉杆BC 组成,A 、B 、C 三处均可简化为铰链约束。起重 荷载kN 22P =F ,m 2=l 。已知MPa 100][=σ,试选择AB 梁的工字钢型号。 解题思路: (1)起重荷载移动到AB 跨中时是最不利情况; (2)研究AB 梁,求BC 杆的受力和A 支座的约束力。AB 梁发生压弯组合变形; (3)分析内力(轴力和弯矩),确定危险截面; (4)先按弯曲正应力强度条件(12-27)设计截面,选择AB 梁的工字钢型号; (5)再按式(10-2)计算危险截面的最大应力值,作强度校核。 答案:选16.No 工字钢 4图示圆截面悬臂梁中,集中力P1F 和P 2F 分别作用在铅垂对称面和水平对称面内,并且垂直 于梁的轴线。已知N 800P1=F ,kN 6.1P2=F ,m 1=l ,许用应力MPa 160][=σ,试确定截面直径d 。 解题思路: (1)圆截面悬臂梁发生在两个互相垂直平面上的平面弯曲的组合变形; (2)分析弯矩y M 和z M ,确定危险截面及计算危险截面上的y M 和z M 值; (3)由式(10-15)计算危险截面的总弯矩值; (4)按弯曲正应力强度条件(12-27)设计截面,确定悬臂梁截面直径d 。 答案:mm 5.59≥d 5功率kW 8.8=P 的电动机轴以转速min /r 800=n 转动,胶带传动轮的直径mm 250=D 组合变形 一、判断题 1.斜弯曲区别与平面弯曲的基本特征是斜弯曲问题中荷载是沿斜向作用的。( ) 2.斜弯曲时,横截面的中性轴是通过截面形心的一条直线。( ) 3.梁发生斜弯曲变形时,挠曲线不在外力作用面内。( ) 4.正方形杆受力如图1所示,A点的正应力为拉应力。( ) 图 1 5. 上图中,梁的最大拉应力发生在B点。( ) 6. 图2所示简支斜梁,在C处承受铅垂力F的作用,该梁的AC段发生压弯组合变形,CB段发生弯曲变形。( ) 图 2 7.拉(压)与弯曲组合变形中,若不计横截面上的剪力则各点的应力状态为单轴应力。( ) 8.工字形截面梁在图3所示荷载作用下,截面m--m上的正应力如图3(C)所示。( ) 图 3 9. 矩形截面的截面核心形状是矩形。( ) 10.截面核心与截面的形状与尺寸及外力的大小有关。( ) 11.杆件受偏心压缩时,外力作用点离横截面的形心越近,其中性轴离横截面的形心越远。( ) 12.计算组合变形的基本原理是叠加原理。() 二、选择题 1.截面核心的形状与()有关。 A、外力的大小 B、构件的受力情况 C、构件的截面形状 D、截面的形心 2.圆截面梁受力如图4所示,此梁发生弯曲是() 图 4 A、斜弯曲 B、纯弯曲 C、弯扭组合 D、平面弯曲 三、计算题 1.矩形截面悬臂梁受力F1=F,F2=2F,截面宽为b,高h=2b,试计算梁内的最大拉应力,并在图中指明它的位置。 图 5 2.图6所示简支梁AB上受力F=20KN,跨度L=2.5m,横截面为矩形,其高h=100mm,宽b=60mm,若已知α=30°,材料的许用应力[σ]=80Mpa,试校核梁的强度。 3.如图7所示挡土墙,承受土压力F=30KN,墙高H=3m,厚0.75m,许用压应力[σ]ˉ=1 Mpa,许用拉应力[σ]﹢=0.1 Mpa,墙的单位体积重量为 ,试校核挡土墙的强度。 图 6 图 7 4.一圆直杆受偏心压力作用,其偏心矩e=20mm,杆的直径d=70mm,许用应力[σ]=120Mpa,试求此杆容许承受的偏心压力F之值。 5.如图8所示,短柱横截面为2a×2a的正方形,若在短柱中间开一槽,槽深为a,问最大应力将比不开槽时增大几倍? 材料力学组合变形习题 L 1AL101ADB (3) 偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点 到形心之距离e和中性轴到形心距离d之间的关系有四种答案: (A ) e=d; (B ) e>d; (C ) e越小,d越大; (D ) e越大,d越小。 正确答案是______。 答案(C ) 1BL102ADB (3) 三种受压杆件如图。设杆1、杆2和杆3中的最大压应力(绝对值)分别用 max1σ、max 2σ和max3σ表示,现有下列四种答案: (A )max1σ=max 2σ=max3σ; (B )max1σ>max 2σ=max3σ; (C )max 2σ>max1σ=max3σ; (D )max 2σ<max1σ=max3σ。 正确答案是______。 答案(C ) 1BL103ADD (1) 在图示杆件中,最大压应力发生在截面上的哪一点,现有四种答案: (A )A点; (B )B点; (C )C点; (D )D点。 正确答案是______。 答案(C ) (A )max1σ<max 2σ<max3σ; (B )max1σ<max 2σ=max3σ; (C )max1σ<max3σ<max 2σ; (D )max1σ=max3σ<max 2σ。 正确答案是______。 答案(C ) 1AL108ADB (3) 图示正方形截面直柱,受纵向力F的压缩作用。则当F力作用点由A点移至B点 时柱内最大压应力的比值()max A σ/()max B σ有四种答案: (A )1:2; (B )2:5; (C )4:7; (D )5:2。 正确答案是______。 答案(C ) 1AL109ADC (2) 一空间折杆受力如图所示,则AB杆的变形有四种答案: (A )偏心拉伸; (B )纵横弯曲; (C )弯扭组合; (D )拉、弯、扭组合。 正确答案是______。 组合变形 、判断题 1?斜弯曲区别与平面弯曲的基本特征是斜弯曲问题中荷载是沿斜向作用的。() 2.斜弯曲时,横截面的中性轴是通过截面形心的一条直线。() 3.梁发生斜弯曲变形时,挠曲线不在外力作用面内。() 4?正方形杆受力如图1所示,A点的正应力为拉应力。() 5.上图中,梁的最大拉应力发生在B点。() 6.图2所示简支斜梁,在C处承受铅垂力F的作用,该梁的AC段发生压弯组合变形,CB段发生弯曲变形。() 7.拉(压)与弯曲组合变形中,若不计横截面上的剪力则各点的应力状态为单轴应力。() 8.工字形截面梁在图3所示荷载作用下,截面m--m上的正应力如图3 (C)所示。 () 4 图3 9. 矩形截面的截面核心形状是矩形。() 10. 截面核心与截面的形 状与尺寸及外力的大小有关。 () 11?杆件受偏心压缩时,外力作用点离横截面的形心越近,其中性轴离横截面的 形心越远。() 12.计算组合变形的基本原理是叠加原理。() 二、选择题 1.截面核心的形状与()有关。 A 、外力的大小B 、构件的受力情况 C 、构件的截面形状 D 、截面的形心 2?圆截面梁受力如图4所示,此梁发生弯曲是() A 、 斜弯曲 B 、 纯弯曲 C 、弯扭组合 ⑹ ⑹ 血 D、平面弯曲 三、计算题 1?矩形截面悬臂梁受力F仁F, F2=2F,截面宽为b,高h=2b,试计算梁内的最大拉应力,并在图中指明它的位置。 2?图6所示简支梁AB上受力F=20KN跨度L=2.5m,横截面为矩形,其高h=100mm, 宽b=60mm,若已知a =30;材料的许用应力[c]=80Mp试校核梁的强度。 3.如图7所示挡土墙,承受土压力F=30KN墙高H=3m,厚0.75m,许用压应力 [c] - =1 MP许用拉应力[丹二Mpa,墙的单位体积重量为m问沪,试校核挡土墙的强度。 4 99 组合变形 1. 偏心压缩杆,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点到形心的距离e 和中性轴到形心的距离d 之间的关系有四种答案: (A) e d =; (B) e d >; (C) e 越小,d 越大; (D) e 越大,d 越大。 答:C 2. 三种受压杆件如图所示,杆1、杆2与杆3中的最大压应力(绝对值)分别为max1σ、max 2σ和 max 3σ,现有下列四种答案: (A)max1max 2max3σσσ==; (B)max1max 2max3σσσ>=; (C)max 2max1max3σσσ>=; (D)max1max3σσσ<=max2。 答:C 3. 重合)。立柱受沿图示a-a (A)斜弯曲与轴向压缩的组合; (B)平面弯曲与轴向压缩的组合; (C)斜弯曲; (D)平面弯曲。 答:B 4. (A) A 点; (B) B 点; (C) C 点; (D) D 点。 答:C 5. 图示矩形截面拉杆,中间开有深度为/2h 的缺口,与不开口的拉杆相比,开口处最大正应力将是不开口杆的 倍: (A) 2倍; (B) 4倍; (C) 8倍; (D) 16倍。 答:C 100 6. 三种受压杆件如图所示,杆1、杆2与杆3中的最大压应力(绝对值)分别为max1σ、max 2σ和max 3σ,现有下列四种答案: (A)max1max 2max3σσσ<<; (B)max1max 2max3σσσ<=; (C)max1max3max 2σσσ<<; (D)max1max3max 2σσσ=<。 答:C 7. 正方形等截面立柱,受纵向压力F 移至B 时,柱内最大压应力的比值max max A B σ σ(A) 1:2; (B) 2:5; (C) 4:7; (D) 5:2。 答:C 8. 图示矩形截面偏心受压杆,其变形有下列四种答案:(A)轴向压缩和平面弯曲的组合; (B)轴向压缩、平面弯曲和扭转的组合; (C)缩和斜弯曲的组合; (D)轴向压缩、斜弯曲和扭转的组合。 答:C 9. 矩形截面梁的高度100mm h =,跨度1m l =。梁中点承受集中力F ,两端受力130kN F =,三力均作用在纵向对称面内,40mm a =。若跨中横截面的最大正应力与最 小正应力之比为5/3。试求F 值。 解:偏心距10mm 2 h e a =-= 跨中截面轴力 N 1F F = 跨中截面弯矩max 14Fl M F e = -(正弯矩) ,或 m a x 14 Fl M F e =-(负弯矩) 一、是非题 9.1 斜弯曲时,危险截面上的危险点是距形心主轴最远的点。() 9.2 工字形截面梁发生偏心拉伸变形时,其最大拉应力一定在截面的角点处。() 9.3 对于偏心拉伸或偏心压缩杆件,都可以采用限制偏心矩的方法,以达到使全部截面上都不出现拉应力的目的。() 9.4 直径为d 的圆轴,其危险截面上同时承受弯矩M 、扭矩T 及轴力N 的作用。若按第三强度理论计算,则危险点处的 9.5 图示矩形截面梁,其最大拉应力发生在固定端截面的a 点处。() 二、选择题 9.6 图( a )杆件承受轴向拉力F ,若在杆上分别开一侧、两侧切口如图( b )、图( c )所示。令杆( a )、( b )、( c )中的最大拉应力分别为和,则下列结论中()是错误的。 A. B. C. D. 9.7 对于偏心压缩的杆件,下述结论中()是错误的。 A. 截面核心是指保证中性轴不穿过横截面的、位于截面形心附近的一个区域 B. 中性轴是一条不通过截面形心的直线 C. 外力作用点与中性轴始终处于截面形心的相对两边 D. 截面核心与截面的形状、尺寸及载荷大小有关 三. 计算题 9.8材料为灰铸铁HT 15-33的压力机框架如图所示。许用拉应力为 ,许用压应力为,试校核该框架立柱的强度。 9.9图示皮带轮传动轴,传递功率N =7kW ,转速n =200 r/min 。皮带轮重量Q =1.8 kN 。左端齿轮上啮合力与齿轮节圆切线的夹角(压力角)为。轴的材料为A5钢,其许用应力。试分别在忽略和考虑皮带轮重量的两种情况下,按第三强度理论估算轴的直径。 答案 9.1 × 9.2 √ 9.3 × 9.4 √ 9.5 √ 9.6 C 9.7 D 9.8解: 习题 [8-1] 14号工字钢悬臂梁受力情况如图所示。已知m l8.0 =,kN F5.2 1 =,kN F0.1 2 =,试求危险截面上的最大正应力。 解:危险截面在固定端,拉断的危险点在前上角点,压断的危险点在后下角,因钢材的拉压性能相同,故只计算最大拉应力: y z y y z z W l F W l F l F W M W M 2 1 1 max 2+ + ? = + = σ 式中, z W, y W由14号工字钢,查型钢表得到3 102cm W z =,3 1. 16cm W y =。故 MPa Pa m m N m m N 1. 79 10 1. 79 10 1. 16 8.0 10 0.1 10 102 2 8.0 10 5.2 3 6 3 6 3 3 6 3 max = ? = ? ? ? + ? ? ? ? ? = - - σ [8-2]矩形截面木檩条的跨度m l4 =,荷载及截面尺寸如图所示,木材为杉木,弯曲许用正应力MPa 12 ] [= σ,GPa E9 =,许可挠度200 / ] [l w=。试校核檩条的强度和刚度。 图 习题?-2 8 解:(1)受力分析 )/(431.13426cos 6.1cos '0m kN q q y ===α )/(716.03426sin 6.1sin '0m kN q q z ===α (2)内力分析 )(432.14716.081 8122max ,m kN l q M z y ?=??=== )(864.24432.18 1 8122max ,m kN l q M y z ?=??=== (3)应力分析 最大的拉应力出现在跨中截面的右上角点,最大压应力出现在左下角点。 z z y y W M W M max ,max ,max + = + σ 式中,32 232266*********mm hb W y ≈?== 32 24693336 1601106mm bh W z ≈?== MPa mm mm N mm mm N 54.1046933310864.232266710432.13 636max =??+??=+ σ (4)强度分析 因为MPa 54.10max =+σ,MPa 12][=σ,即][max σσ<+,所以杉木的强度足够。 (5)变形分析 最大挠度出现在跨中,查表得: z y cy EI l q w 38454 = ,y z cz EI l q w 38454 = 第十章 组合变形 10-2 图a 所示板件,b =20mm , =5mm ,载荷F = 12 kN ,许用应力[] = 100 MPa , 试求板边切口的允许深度x 。 题10-2图 解:在切口处切取左半段为研究对象(图b ),该处横截面上的轴力与弯矩分别为 F F =N )(a b F M -= (a) 显然, 2 22x b x b a -=-= (b) 将式(b)代入式(a),得 2 Fx M = 切口段处于弯拉组合受力状态,该处横截面上的最大拉应力为 2 2N max 432(2a)6 22a Fx a F Fx a F W M A F δδδδσ+ =+=+= 根据强度要求,在极限情况下, ][4322 σδδ=+a Fx a F 将式(b)与相关数据代入上式,得 01039.61277.042=?+--x x 由此得切口的允许深度为 m m 20.5=x 10-3 图示矩形截面钢杆,用应变片测得上、下表面的纵向正应变分别为a ε=×10 -3 与b ε=×10-3 ,材料的弹性模量E =210GPa 。试绘横截面上的正应力分布图,并求拉力F 及其偏心距e 的数值。 题10-3图 解:1.求a σ和b σ 截面的上、下边缘处均处于单向受力状态,故有 MPa 84Pa 104.010210 MPa 210Pa 100.1102103 9 39=???===???==--b b a a E εσE εσ 偏心拉伸问题,正应力沿截面高度线性变化,据此即可绘出横截面上的正应力分布图,如图10-3所示。 图10-3 2.求F 和e 将F 平移至杆轴线,得 Fe M F F ==,N 于是有 a z a E εW Fe A F σ=+= E εW Fe A F σz b =-= 代入相关数据后,上述方程分别成为 26250240=+Fe F 10500240=-Fe F 材 料 力 学 ·198 · 第9章 构件/组合变形 9.1 概 述 前面章节讨论了杆件在拉伸(压缩)、剪切、扭转和弯曲等基本变形形式下的应力和位移的计算等问题。工程实际中的许多构件往往发生两种或两种以上基本变形,称为组合变形。例如,钻探机钻杆(图9.1(a ))上端受到来自动力机械的力螺旋(力+力偶)作用引起的轴向压缩变形,下部受到来自泥土的分布力螺旋作用引起的扭转变形;蓄水堤(图9.1(b ))受自重引起的轴向压缩变形,同时还有水平的水压引起的弯曲变形;又如机械中齿轮传动轴(图9.1(c ))在啮合力作用下,将同时发生扭转变形以及在水平和竖直平面内的弯曲变形;再如厂房中支撑吊车梁的立柱(图9.1(d ))在由吊车梁传来的不通过立柱轴线的竖直载荷作用下,引起的偏心压缩变形,它可看成是轴向压缩和纯弯曲的组合变形。 图9.1 组合变形实例 对于组合变形下的构件,在线弹性范围内,小变形条件下,可按构件的原始形状和尺寸进行计算。因而,可先将载荷化为符合基本变形外力作用条件的外力系,分别计算构件在每一种基本变形下的内力、应力或变形。然后,利用叠加原理,综合考虑各种基本变形的组合情形,以确定构件的危险截面、危险点的位置及危险点处的应力状态,并据此进行强度计算。 利用叠加原理进行组合变形构件的强度分析计算过程可概括为: (1)按引起的变形类型分解外力。通常是将载荷向杆件的轴线和形心主惯轴简化,把组合变形分解为几个基本变形。 第9章 构件/组合变形 ·199 · (2)分别绘出各基本变形的内力图,确定危险截面位置,再根据各种变形应力分布规律,确定危险点。 (3)分别计算危险点处各基本变形引起的应力。 (4)叠加危险点的应力。叠加通常是在应力状态单元体上的进行。然后选择适当的强度理论进行强度计算。 若构件的组合变形超出了线弹性范围,或虽在线弹性范围内但变形较大,则不能按其初始形状或尺寸进行计算,必须考虑各基本变形之间的相互影响,此时不能用叠加原理。 本章主要讨论在实际工程中常见组合变形:拉(压)弯组合、弯扭组合、斜弯曲等。 9.2 轴向拉伸(压缩)与弯曲的组合 杆件受轴向拉伸(压缩)与弯曲的组合作用有两种情况:一种是轴向载荷与横向载荷的联合作用,另一种是偏心拉伸或压缩。 若杆受到轴向载荷作用的同时,又在其纵向平面内受到横向载荷的作用,这时杆件将发生轴向拉伸(压缩)与弯曲的组合变形。对于弯曲刚度较大的杆件,由于横向力引起的挠度与横截面的尺寸相比很小,原始尺寸原理可以使用,轴向力因弯曲变形而产生的弯矩可以省略不计。这样,轴向力就只引起压缩变形,外力与杆件内力和应力的关系仍然是线性的,叠加原理就可以使用。可分别计算由横向力和轴向力引起的杆横截面上的正应力,按叠加原理求其代数和,即得在拉伸(压缩)与弯曲组合变形下杆横截面上的正应力。 下面以图9.2所示的简支梁为例,说明杆受轴向载荷与横向载荷联合作用下的应力及强度计算方法。该简支梁承受轴向载荷F 与横向均布载荷q 的联合作用。轴向载荷F 使梁产生轴向伸长,引起各横截面的轴力均为F N =F (图9.2(c ));横向载荷q 使梁发生在xy 平面 内的弯曲,跨中截面C 的弯矩最大,其值为2max /8C M M ql ==(图9.2(d ))。显然,截面C 是危险截面(剪力引起的切应力通常忽略不计),如图9.2(b )所示。 在危险截面上,由轴力F N 引起的正应力N F σ为 N N F F A σ= 纵坐标为y 处,弯矩C M 引起的弯曲正应力M σ为 max M z M y I σ= 应用叠加原理,可得危险截面上任一点处的正应力 (9.1) 上式表明,正应力沿截面高度呈线性变化,且中性轴不通过截面形心。截面底部边缘和顶部边缘处的正应力分别为 (9.2) 8-1 14号工字钢悬臂梁受力情况如图所示。已知m,,,试求危险截面上的最大正应力。 解:危险截面在固定端 = = 返回 8-2 受集度为的均布荷载作用的矩形截面简支梁,其荷载作用面与梁的纵 向对称面间的夹角为,如图所示。已知该梁材料的弹性模量; 梁的尺寸为m,mm,mm;许用应力;许可挠度 。试校核梁的强度和刚度。 解: = ,强度安全 , = =刚度安全。 返回 8-3(8-5)图示一悬臂滑车架,杆AB为18号工字钢,其长度为m。试 求当荷载作用在AB的中点D处时,杆内的最大正应力。设工字钢的自重可略去不计。 解:18号工字钢,,AB杆系弯压组合变形。 ,, == == 返回 8-4(8-6)砖砌烟囱高m,底截面m-m的外径m,内径m, 自重kN,受的风力作用。试求: (1)烟囱底截面上的最大压应力; (2)若烟囱的基础埋深m,基础及填土自重按计算,土壤的 许用压应力,圆形基础的直径D应为多大? 注:计算风力时,可略去烟囱直径的变化,把它看作是等截面的。 解:烟囱底截面上的最大压应力: == 土壤上的最大压应力: 即 即 解得:m 返回 8-5(8-8)试求图示杆内的最大正应力。力F与杆的轴线平行。 解:,z为形心主轴。 固定端为危险截面,其中: 轴力,弯矩, = A点拉应力最大 == B点压应力最大 == 因此 返回 8-6(8-9) 有一座高为1.2m、厚为0.3m的混凝土墙,浇筑于牢固的基础上,用作挡水用的小坝。试求: (1)当水位达到墙顶时墙底处的最大拉应力和最大压应力(设混凝土 的密度为); (2)如果要求混凝土中没有拉应力,试问最大许可水深h为多大? 解:以单位宽度的水坝计算: 水压: 混凝土对墙底的压力为: 墙坝的弯曲截面系数: 墙坝的截面面积: 墙底处的最大拉应力为: 第12章组合变形的强度计算 主要知识点:(1)弯曲与拉伸(压缩)组合变形的强度计算; (2)弯曲与扭转组合变形的强度计算。 1. 试判断图中杆AB、BC和CD各产生哪些基本变形? 答:如图12-1a所示,将力F平移到B点,可知图中杆AB 产生弯曲变形; 如图12-1b所示,将力F平移到C点,可知杆BC产生 压缩和弯曲组合变形; 如图12-1c所示,杆CD产生(横力)弯曲变形。 a) b) c) 图12-1 2. 若在正方形截面短柱的中间处开一个槽,如图所示,使横截面面积减少为原截面面积的一半。试求最大正应力比不开槽时增大几倍? 解:正方形短柱截面不开槽时最大正应力 2 04a F A F= = σ 正方形短柱截面开槽时,BC段受偏心压缩,偏心距e=0.5a, 抗弯截面系数3/3a W Z =,最大正应力 2 3 2 1 max 2 3 5.0 2a F a a F a F W Fe A F Z = ? + = + = σ max σ/8 = σ,所以开槽后最大正应力比不开槽时增大7倍。 3.如图所示的支架,已知载荷F=45kN,作用在C处,支架材料的许用应力 [] a MP 160 = σ,试选择横梁AC的工字钢型号。 解:(1)外力分析 作ABC梁的受力图,如图12-3a所示。 平衡方程 30 sin ,0 ) (0 1 = ? - ? = ∑ = AC F AB F F M B n i i A 图12-3 解得kN F B 120=。由受力图可知,梁的AB 段为拉伸与弯曲的组合变形,而BC 段为弯曲变形。 (2)内力分析,确定危险截面的位置 AB 段受到拉力,kN F F B N 10430cos 0==,作出图12-3b 所示轴力图。 梁的AB 段、BC 段剪力均为常数,弯矩图均为斜直线,算得m kN M B ?-=45,作出图12-3c 所示弯矩图。故危险截面是B -截面,即B 截面左侧。 危险截面上的轴力kN F N 104=、弯矩m kN M B ?-=45 (3)应力分析,确定危险点的位置 危险截面上拉伸正应力A F N =1σ,弯曲正应力y I M Z max 2=σ(见图12-3d )。根据危险截面上的应力分布规律可知,危险点在危险截面的上侧边缘。其最大应力值为 Z N W M A F max max +=σ (4)强度计算 因危险点的应力为单向应力状态,所以其强度条件为 []σσ≤?+?=+=Z Z N W A W M A F 33max max 104510104a MP 160= (a) 因上式中有截面面积A 和抗弯截面系数W Z 两个未知量,故要用试凑法求解。用这种方法求解时,可先不考虑轴力N F 的影响,仅按弯曲强度条件初步选择槽钢的型号,然后再按(a)式进行校核。由 []a Z Z P W W M 63max max 101601045?=≤?==σσ 得336328110 1601045cm m W Z =??≥。查表得22a 工字钢3309cm W Z =,代入(a)式进行校核第八章组合变形构件的强度习题
第八章组合变形练习题
最新10组合变形汇总
《材料力学》第8章 组合变形及连接部分的计算 习题解
材料力学习题组合变形
第八章组合变形构建的强度习题答案_百度文库.
精选题10组合变形
工程力学A参考习题之组合变形解题指导
组合变形 习题及答案
材料力学组合变形习题
组合变形习题及参考答案
精选题10组合变形
第九章 组合变形
第八章组合变形及连接部分的计算习题测验选解
ch10组合变形
第9章构件组合变形
材料力学 组合变形及连接部分计算答案
组合变形习题解答