第9章构件组合变形
- 格式:pdf
- 大小:505.98 KB
- 文档页数:18





第9章 钢筋混凝土构件的变形和裂缝9.1选择题1.下面的关于受弯构件截面弯曲刚度的说明错误的是( D )。
A . 截面弯曲刚度随着荷载增大而减小;B . 截面弯曲刚度随着时间的增加而减小;C . 截面弯曲刚度随着变形的增加而减小;D . 截面弯曲刚度不变;2.钢筋混凝土构件变形和裂缝验算中关于荷载、材料强度取值说法正确的是(B )。
A . 荷载、材料强度都取设计值;B . 荷载、材料强度都取标准值;C . 荷载取设计值,材料强度都取标准值;D . 荷载取标准值,材料强度都取设计值;3.钢筋混凝土受弯构件挠度计算公式正确的是( D )。
A .sk B l M S f 2=;B .B l M S f k 2=;C .sq B l M S f 2=;D .B l M S f q 2=;4.下面关于短期刚度的影响因素说法错误的是( B )。
A .ρ增加,sB 略有增加;B .提高混凝土强度等级对于提高s B 的作用不大;C .截面高度对于提高s B 的作用的作用最大;D .截面配筋率如果满足承载力要求,基本上也可以满足变形的限值;5.《混凝土结构设计规范》定义的裂缝宽度是指:( B )。
A . 受拉钢筋重心水平处构件底面上混凝土的裂缝宽度;B . 受拉钢筋重心水平处构件侧表面上混凝土的裂缝宽度;C . 构件底面上混凝土的裂缝宽度;D . 构件侧表面上混凝土的裂缝宽度;6.减少钢筋混凝土受弯构件的裂缝宽度,首先应考虑的措施是( A )。
A . 采用直径较细的钢筋;B . 增加钢筋的面积;C . 增加截面尺寸;D.提高混凝土强度等级;7.混凝土构件的平均裂缝间距与下列哪个因素无关( A )。
A.混凝土强度等级;B.混凝土保护层厚度;C.纵向受拉钢筋直径;D.纵向钢筋配筋率;8.提高受弯构件截面刚度最有效的措施是( D )。
A.提高混凝土强度等级;B.增加钢筋的面积;C.改变截面形状;D.增加截面高度;9.关于受弯构件裂缝发展的说法正确的是( C )。



第9章钢筋混凝土构件的变形、裂缝验算及耐久性一、填空题1.混凝土构件裂缝开展宽度及变形验算属于正常使用极限状态的设计要求,验算时材料强度采用标准值,荷载采用标准值、准永久值。
2. 增大构件截面高度是提高钢筋混凝土受弯构件抗弯刚度的最有效措施。
3.平均裂缝宽度计算公式中,σ是指裂缝截面处的纵向钢筋拉应力,其值是按荷载sk效应的标准组合计算的。
4.钢筋混凝土构件的平均裂缝间距随混凝土保护层厚度增大而增大,随纵筋配筋率增大而减小。
5.钢筋混凝土受弯构件挠度计算中釆用的最小刚度原则是指在相同符号弯矩范围内,假定其刚度为常数,并按最大弯矩截面处的最小刚度进行计算。
6.裂缝间纵向受拉钢筋应变不均匀系数ψ是指裂缝间受拉纵筋平均应变与裂缝截面处的受拉纵筋应变之比,反映了裂缝间拉区混凝土参与工作的程度。
7.结构构件正常使用极限状态的要求主要指在各种作用下的裂缝宽度和变形不应超过规定的限值。
8.结构的耐久性设计要求是指结构构件应满足设计使用年限的要求。
9.混凝土结构应根据使用环境类别和结构类别进行耐久性设计。
10.在荷载作用下,截面受拉区混凝土中出现裂缝,裂缝宽度与受拉纵筋应力几乎成正比。
11.钢筋混凝土和预应力混凝土构件,按所处环境类别和结构类别确定相应的裂缝控制等级最大裂缝宽度限值。
12.平均裂缝间距与混凝土保护层厚度、纵向受拉钢筋直径、纵向受拉钢筋表面特征系数及纵向钢筋配筋率有关。
13.轴心受拉构件的平均裂缝宽度为构件裂缝区段范围内钢筋的平均伸长与相应水平处构件侧表面混凝土平均伸长之差。
14.最大裂缝宽度等于平均裂缝宽度乘以扩大系数,这个系数是考虑裂缝宽度的随机性以及长期荷载作用的影响。
15.受弯构件的最大挠度应按荷载效应的标准组合,并考虑荷载长期作用影响进行计算。
16.结构构件正截面的裂缝控制等级分为三级。
17.环境类别中一类环境是指室内正常环境。
二、选择题1.减少钢筋混凝土受弯构件的裂缝宽度,首先应考虑的措施是[ a ]。

第一章绪论1.土木工程中,各种建筑物在施工和使用阶段所承受的所有外力统称为荷载。
建筑物中承受荷载并且传递荷载的空间骨架称为结构,而任何结构都是由构件所组成的。
为保证构件在荷载作用下的正常工作,必须使它同时满足三方面的力学要求,即强度、刚度和稳定性的要求:(1) 构件抵抗破坏的能力称为强度(strength)。
对构件的设计应保证它在规定的荷载作用下能够正常工作而不会发生破坏(2) 构件抵抗变形的能力称为刚度(stiffness)。
构件的变形必须要限制在一定的限度内,构件刚度不满足要求同样也不能正常工作。
(3) 构件在受到荷载作用时在原有形状下的平衡应保证为稳定的平衡,这就是对构件的稳定性(stability)要求。
但是在材料力学中,构件的变形不能忽略不计,因此我们把构件作为可变形体来研究,称它们为可变形固体(deformable solid)。
在对可变形固体材料制成的构件进行强度、刚度和稳定性研究时,为抽象出某种理想的力学模型,通常根据其主要性质做出一定的假设,同时忽略一些次要因素,然后进行理论分析。
在材料力学中,通常对可变形固体作如下基本假设:(1) 连续性假设(continuity assumption)。
这一假设认为,构件的材料在变形后仍然保持连续性,在其整个体积内都毫无空隙地充满了物质,忽略了体积内空隙对材料力学性质的影响。
(2) 均匀性假设(homogenization assumption)。
这一假设认为,构件的材料各部分的力学性能是相同的。
从任意一点取出的单元体,都具有与整体同样的力学性能。
(3) 各向同性假设(isotropy assumption)。
这一假设认为,构件的材料在各个方向的力学性能是相同的。
如工程上常用的金属材料,虽然从它们的晶粒来说,其力学性能并不一样;但从宏观上看,各个方向的力学性能接近相同。
有些材料沿各方向的力学性能并不相同,像这样的材料称之为各向异性材料,如木材等。

钢筋混凝土结构辅导资料十四主题:第九章钢筋混凝土构件的变形和裂缝计算的辅导资料——钢筋混凝土受弯构件挠度验算;钢筋混凝土构件裂缝宽度验算。
学习时间:2014年12月29日-2015年1月4日内容:这周我们学习第九章的第一部分,学习本章时,重要的是要搞清一些概念和原理,而对一些公式,例如截面弯曲刚度和裂缝最大宽度的计算公式以及一些系数的计算公式是不要求背的,但对这些系数的物理意义是要知道的。
一、学习要求1.理解钢筋混凝土构件截面弯曲刚度的定义、基本表达式、主要影响因素以及裂缝间钢筋应变不均匀系数的物理意义;2.掌握简支梁、板的挠度验算方法;基本内容:二、主要内容根据钢筋混凝土结构物的某些工作条件以及使用要求,在钢筋混凝土结构设计中,除需要进行承载能力极限状态计算外,还应进行正常使用极限状态(即裂缝与变形)的验算,同时还应满足在正常使用下的耐久性的要求。
对结构构件进行变形验算和控制的目的是出于对结构的功能、非结构构件的损坏和外观的要求。
结构构件产生过大的变形会损害甚至使构件完全丧失所应负担的使用功能,如吊车梁变形过大将使吊车轨道歪斜而影响吊车的正常运行;构件过度变形会引起非结构构件的破坏,如建筑物中脆性隔墙(如石膏板、灰砂砖等)的开裂和损坏很多是由于支承它的构件变形过大所致;构件出现明显下垂的挠度会使房屋的使用者产生不安全感。
我国《规范》将配筋混凝土结构构件裂缝控制等级划分为三级。
一级——严格要求不出现裂缝的构件,按荷载效应的标准组合进行计算时,钢筋混凝土构件的变形︑裂缝及混凝土结构的截面弯曲刚度的概念和定短期刚度Bs ,裂缝间纵向受拉钢筋应变不均匀系数,截最小刚度原则与挠度验算,影响Bs 的主要因裂缝出现、分布和开展的机理 平均裂缝间距和平均裂缝宽度 最大裂缝宽度及其验算方法,影响裂缝宽度的主混凝土构件截面延性的概念 受弯构件的截面曲率延性系数,偏心受压构件截面曲率延混凝土结构耐久性的概念及其主要影响因素 混凝土的碳化,钢筋的锈蚀,耐久性构件受拉边缘混凝土不应产生拉应力。
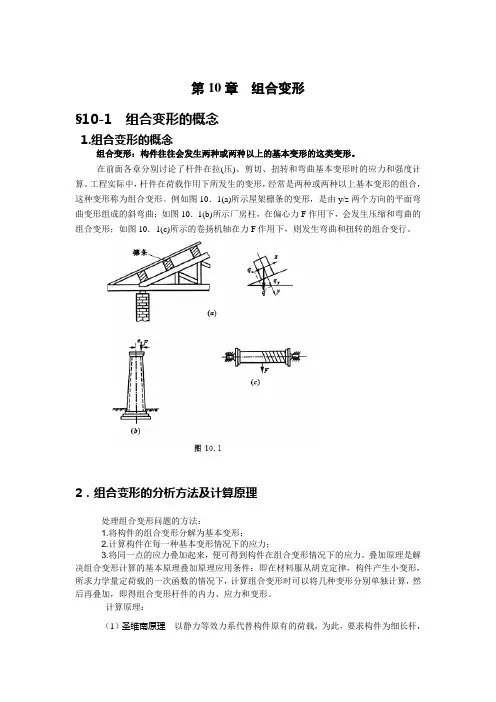
第10章组合变形§10-1 组合变形的概念1.组合变形的概念组合变形:构件往往会发生两种或两种以上的基本变形的这类变形。
在前面各章分别讨论了杆件在拉(压)、剪切、扭转和弯曲基本变形时的应力和强度计算。
工程实际中,杆件在荷载作用下所发生的变形,经常是两种或两种以上基本变形的组合,这种变形称为组合变形。
例如图10.1(a)所示屋架檩条的变形,是由y/z两个方向的平面弯曲变形组成的斜弯曲;如图10.1(b)所示厂房柱,在偏心力F作用下,会发生压缩和弯曲的组合变形;如图10.1(c)所示的卷扬机轴在力F作用下,则发生弯曲和扭转的组合变行。
2.组合变形的分析方法及计算原理处理组合变形问题的方法:1.将构件的组合变形分解为基本变形;2.计算构件在每一种基本变形情况下的应力;3.将同一点的应力叠加起来,便可得到构件在组合变形情况下的应力。
叠加原理是解决组合变形计算的基本原理叠加原理应用条件:即在材料服从胡克定律,构件产生小变形,所求力学量定荷载的一次函数的情况下,计算组合变形时可以将几种变形分别单独计算,然后再叠加,即得组合变形杆件的内力、应力和变形。
计算原理:(1)圣维南原理以静力等效力系代替构件原有的荷载,为此,要求构件为细长杆,且所求应力的截面远离外力作用点;(2)叠加原理 按各基本变形计算后进行叠加,为此,要求构件处于线弹性范围内,且变形很小,可按构件的原始形状的尺寸进行计算。
在小变形和线弹性条件下,杆件上各种力的作用彼此独立,互不影响,即杆上同时有几种力作用时,一种力对杆的作用效果(变形或应力),不影响另一种力对杆的作用效果(或影响很小可以忽略)。
因此组合变形下杆件内的应力,可视为几种基本变形下杆件内应力的叠加。
本章中组合变形下杆件的应力计算,将以各基本变形的应力及叠加法为基础。
叠加法的主要步骤:a 、将组合变形按照各基本变形的条件,分解为几种基本变形,简称分解。
b 、利用基本变形的应力计算公式,分别计算各点处的正应力和切应力。
材料⼒学试卷及答案⼀、低碳钢试件得拉伸图分为、、、四个阶段。
(10分)⼆、三⾓架受⼒如图所⽰。
已知F=20kN,拉杆BC采⽤Q235圆钢,[σ钢]=140MPa,压杆AB采⽤横截⾯为正⽅形得松⽊,[σ⽊]=10MPa,试⽤强度条件选择拉杆BC得直径d与压杆AB得横截⾯边长a。
(1n=180r/min,材料得许⽤切分)2六、单元体应⼒如图所⽰,试计算主应⼒,并求第四强度理论得相当应⼒。
(10分)e =200m⼋、图⽰圆杆直径d =100mm,材料为Q235钢,E =200GP a,λp =100,试求压杆得临界⼒F cr 。
(10《材料⼒学》试卷(1)答案及评分标准⼀、弹性阶段、屈服阶段、强化阶段、颈缩断裂阶段。
评分标准:各2、5分。
⼆、d=15mm ; a =34mm.评分标准:轴⼒5分, d 结果5分,a 结果5分。
三、τ=87、5MPa, 强度⾜够. 评分标准:T3分,公式4分,结果3分。
四、评分标准:受⼒图、⽀座反⼒5分,剪⼒图55分。
五、σmax =155、8M Pa]=100 M P,但没超过许⽤应⼒得5%,安全. 评分标准:弯矩5分, 3分,正应⼒公式5分结果2分。
六、(1)σ1=141、42 M Pa,σ=0,σ3=141、42 MP a;(2)σr 4=245 M Pa。
评分标准:主应⼒5分,相当应⼒5分。
七、σmax =0、64 MPa,σmin =-6、04 MPa 。
评分标准:内⼒5分,公式6分,结果4分。
⼋、F c r =53、39kN评分标准:柔度3分,公式5分,结果2分。
⼀、什么就是强度失效、刚度失效与稳定性失效?⼆、如图中实线所⽰构件内正⽅形微元,受⼒后变形为图中虚线得菱形,则微元得剪应变为?A 、B 、C、 D 、答案:D三、材料⼒学中得内⼒就是指( )。
A 、物体内部得⼒。
B 、物体内部各质点间得相互作⽤⼒。
C 、由外⼒作⽤引起得各质点间相互作⽤⼒得改变量。
D、由外⼒作⽤引起得某⼀截⾯两侧各质点间相互作⽤⼒得合⼒得改变量。
第九章 组合变形部分填空题01. ( 5 ) 偏心压缩实际不就是 ________ 和 ___________ 的组合变形问题 02.( 5 ) 铸铁构件受力如图所示,其危险点的位置有四中种答案: ( A ) ① 点; ( B ) ② 点; ( C )③ 点; ( D ) ④ 点。
正确答案是 ____________03.(5)图示矩形截面拉杆中间开一深度为 h/2 的缺口,与不开口的拉杆相比,开中处的最大应力的增大倍数有 四种答案:(A) 2 倍; (B) 4 倍; (C) 8 倍; (D) 16 倍;正确答案是 ____________表示,它们之间的关系有四种答案:正确答案是___________04.三种受压杆件如图,设杆 1、2、和杆 3 中的最大压应力 (绝对值) 分别用max1 max2 和max3A )max1< max2 < m ax3 ; m ax1 < max2 = max3 ;max1 max3 max2max1 max3 max205. 一空间折杆受力如图所示,则 AB 杆的变形有四种答案:(A) 偏心拉伸; ( B ) 纵横弯曲; ( C ) 弯扭组合; ( D ) 拉弯扭组合; 正确答案是 _________________ 。
06. 图示正方形截面杆承受弯扭组合变形,在进行强度计算时,其任一截面的危险点位置有四种答案:(A) 截面形心; ( B ) 竖边中点 A 点; ( C ) 横边中点 B 点; ( D ) 横截面的角点 D点; 正确答案是 _________ 。
08 用第三强度理论校核图示杆的强度时,有四种答案:(A) P/ A [(M /W z )24(T /W t )2]1/2 [ ] ;(B) P/ A M /W z T /W t [ ] ; (C) [(P/ A M /W z )2(T /W t )2]1/2 [ ];07. 折杆危险截面上危险点的应力状态,现有四种答案: 正确答案是 。
材 料 力 学·198· 第9章 构件/组合变形9.1 概 述前面章节讨论了杆件在拉伸(压缩)、剪切、扭转和弯曲等基本变形形式下的应力和位移的计算等问题。
工程实际中的许多构件往往发生两种或两种以上基本变形,称为组合变形。
例如,钻探机钻杆(图9.1(a ))上端受到来自动力机械的力螺旋(力+力偶)作用引起的轴向压缩变形,下部受到来自泥土的分布力螺旋作用引起的扭转变形;蓄水堤(图9.1(b ))受自重引起的轴向压缩变形,同时还有水平的水压引起的弯曲变形;又如机械中齿轮传动轴(图9.1(c ))在啮合力作用下,将同时发生扭转变形以及在水平和竖直平面内的弯曲变形;再如厂房中支撑吊车梁的立柱(图9.1(d ))在由吊车梁传来的不通过立柱轴线的竖直载荷作用下,引起的偏心压缩变形,它可看成是轴向压缩和纯弯曲的组合变形。
图9.1 组合变形实例对于组合变形下的构件,在线弹性范围内,小变形条件下,可按构件的原始形状和尺寸进行计算。
因而,可先将载荷化为符合基本变形外力作用条件的外力系,分别计算构件在每一种基本变形下的内力、应力或变形。
然后,利用叠加原理,综合考虑各种基本变形的组合情形,以确定构件的危险截面、危险点的位置及危险点处的应力状态,并据此进行强度计算。
利用叠加原理进行组合变形构件的强度分析计算过程可概括为:(1)按引起的变形类型分解外力。
通常是将载荷向杆件的轴线和形心主惯轴简化,把组合变形分解为几个基本变形。
第9章 构件/组合变形·199· (2)分别绘出各基本变形的内力图,确定危险截面位置,再根据各种变形应力分布规律,确定危险点。
(3)分别计算危险点处各基本变形引起的应力。
(4)叠加危险点的应力。
叠加通常是在应力状态单元体上的进行。
然后选择适当的强度理论进行强度计算。
若构件的组合变形超出了线弹性范围,或虽在线弹性范围内但变形较大,则不能按其初始形状或尺寸进行计算,必须考虑各基本变形之间的相互影响,此时不能用叠加原理。
本章主要讨论在实际工程中常见组合变形:拉(压)弯组合、弯扭组合、斜弯曲等。
9.2 轴向拉伸(压缩)与弯曲的组合杆件受轴向拉伸(压缩)与弯曲的组合作用有两种情况:一种是轴向载荷与横向载荷的联合作用,另一种是偏心拉伸或压缩。
若杆受到轴向载荷作用的同时,又在其纵向平面内受到横向载荷的作用,这时杆件将发生轴向拉伸(压缩)与弯曲的组合变形。
对于弯曲刚度较大的杆件,由于横向力引起的挠度与横截面的尺寸相比很小,原始尺寸原理可以使用,轴向力因弯曲变形而产生的弯矩可以省略不计。
这样,轴向力就只引起压缩变形,外力与杆件内力和应力的关系仍然是线性的,叠加原理就可以使用。
可分别计算由横向力和轴向力引起的杆横截面上的正应力,按叠加原理求其代数和,即得在拉伸(压缩)与弯曲组合变形下杆横截面上的正应力。
下面以图9.2所示的简支梁为例,说明杆受轴向载荷与横向载荷联合作用下的应力及强度计算方法。
该简支梁承受轴向载荷F 与横向均布载荷q 的联合作用。
轴向载荷F 使梁产生轴向伸长,引起各横截面的轴力均为F N =F (图9.2(c ));横向载荷q 使梁发生在xy 平面 内的弯曲,跨中截面C 的弯矩最大,其值为2max /8C M M ql ==(图9.2(d ))。
显然,截面C 是危险截面(剪力引起的切应力通常忽略不计),如图9.2(b )所示。
在危险截面上,由轴力F N 引起的正应力N F σ为N N F F Aσ=纵坐标为y 处,弯矩C M 引起的弯曲正应力M σ为 max M zM y I σ= 应用叠加原理,可得危险截面上任一点处的正应力(9.1)上式表明,正应力沿截面高度呈线性变化,且中性轴不通过截面形心。
截面底部边缘和顶部边缘处的正应力分别为(9.2)材 料 力 学·200·图9.2 拉弯组合变形实例及C 截面应力叠加分析式中,max c σ是压应力还是拉应力或是零,要视具体情况而定。
图9.3(e )所示为max z M W >NF A的情形。
因为截面底部边缘和顶部边缘处均处于单向应力状态,当tmax σ和cmax σ确定后,即可由强度条件进行正应力强度计算,即 t max σ≤t []σ, c max σ≤c []σ (9.3)【例9.1】 小型压力机的铸铁框架如图9.3(a )所示。
已知材料的许用拉应力[σt ] = 35 MPa ,许用压应力[σc ] = 170 MPa ,Z 0 = 85 mm ,44814410mm y I =×。
试按立柱的强度确定压力机的许可压力F 。
【解】:取截面n − n 上半部分为研究对象,其受力如图9.3(b )所示。
由此可知压力机的立柱部分发生拉伸和弯曲的组合变形,像立柱这样受力情形有时称为偏心拉伸。
容易求得横截面n − n 上的轴力F N 和弯矩M y 分别为N F F = 485y M F =横截面上由轴力N F引起正应力为均布拉应力,且NN 2160mm 60mm 219200mm F F F F A σ===××(拉应力)图9.3 例9.1图(单位:mm )第9章 构件/组合变形·201· 由弯矩M y 引起的最大弯曲正应力为0t max 448585MPa 814410y y My M z F I σ×==×,(拉应力) 1cmax4485135MPa 814410y y M y M z F I σ×==×,(压应力) 应用叠加法叠加以上内力引起的应力,可得n n −截面内侧的最大拉应力t max σ,并由强度条件计算许可压力N t max ,t max t 448585[]35MPa 19200814410F My F F σσσσ×=+=+=×≤ 求解得[]62700N 62.7kN F =≤同理可求得,n n −截面外侧的最大压应力c max σ,并由强度条件计算许可压力N c max ,c max c 4485135[]170MPa 19200814410y F M F F σσσσ×=+=−=×≤ 求解得[]226100N 226.1kN F =≤综上所述,为使压力机的立柱同时满足抗拉和抗压强度条件,[]62.7kN F ≤。
【例9.2】 悬臂吊车如图9.4(a )所示,最大起吊重量为F = 28 kN 。
横梁AB 为工字钢制成,材料为Q 235钢,[σ] = 100 MPa 。
试选择工字钢型号。
【解】:横梁AB 的受力简图如图9.4(b )所示,由平衡方程0A m =∑,得N sin 30 2.4 1.20AB F F °×−=i解得 N 28kN AB F F ==将N AB F 按图9.4(b )所示分解为x F 和y F ,显然x F 使得横梁AB 轴向受压,y F 使得横梁AB 发生平面弯曲,可见横梁AB 发生轴向压缩与平面弯曲的组合变形,且cos30kN x F F == , sin 3014kN y F F ==图9.4 例9.2图材 料 力 学·202· 由横梁AB 的受力图可看出,中间截面D 为危险截面。
最大压应力c max σ发生在该截面的上边缘,即为危险点。
为了计算方便,在开始计算时,可以先不考虑轴力的影响,只根据弯曲强度条件选取工字钢。
这时[]6333max 1.21410N mm 16810mm 168cm 100MPaz M W σ××==×=i > 查附录型钢表,选取No.18工字钢,3185cm z W =,230.756cm A =。
选定工字钢后,同时考虑轴力F N 及弯矩M 的影响,再进行强度校核。
在危险截面D 的上边缘各点发生最大压应力,为36N max c max 223310N 1.21410N mm 98.7MPa []30.75610mm 18510mm zF M A W σσ××=+=+=××i ≤ 可见,选择No.18工字钢满足强度需要。
本题若还需考虑工字钢的自重,则应选什么型号的工字钢?请读者自行考虑。
【例9.3】 图9.5(a )所示的高铁矩形截面桥墩立柱,单向行驶动车传递的铅垂压力P 的作用点位于y 轴上,P 、b 、h 均为已知。
试确定在桥墩立柱的横截面上不出现拉应力的最大偏心距e 。
【解】:将外力P 向C 截面形心平移,得作用线与立柱轴线重合的压力P 和作用于xy 平面内的力偶m P e =i 。
在P 和m 共同作用下,立柱BC 段产生压缩和弯曲的组合变形,如图9.5(b )所示。
在轴向压力P 单独作用下,BC 段各横截面上的轴力均为N F P =−;在平面力偶m 单独作用下,BC 段各横截面上的弯矩均为z M Pe =。
可见,BC 段内的各横截面均为危险截面。
由轴力N F 引起的横截面上各点的压应力均相等,即N F P Aσ=−;由弯矩引起的横截面上的弯曲正应力沿截面高度按线性分布,横截面左边线(立柱BC 段左侧面)为最大拉应力,横截面右边线(立柱BC 段右侧面)为最大压应力,最大弯曲拉、压正应力,t max M σ、,cmax M σ其大小均为zPe W 。
应力分布分别如图9.5(c )、图9.5(d )所示。
图9.5 例9.3图第9章 构件/组合变形·203· 欲使BC 段任一横截面上不出现拉应力,应使P 与m 共同作用下横截面左侧边缘各点处叠加后的最大拉应力t max σ等于或小于零,即N tmax ,tm ax 0F M zP Pe A W σσσ=+=−+≤ 得 20/6P Pe bh bh −+ 解得6h e ≤,即6h e =为所求的最大偏心距。
由此可知,当压力P 作用在y 轴上时,只要偏心距6h e ≤,横截面上就不会出现拉应力。
由本例可推断,在截面上总可以找到一个区域(包含截面形心),当偏心力作用点位于此区域之内或其边界上时,横截面上只出现一种性质的应力(偏心拉伸时为拉应力,偏心压缩时为压应力)。
截面形心附近的这样一个区域就称为截面核心。
在工程上,常用的脆性材料(如砖、石、混凝土、铸铁等)抗压性能好而抗拉性能差,因而由这些材料制成的偏心受压构件,应当力求使其全截面上只出现压应力而不出现拉应力,即P 应尽量作用于截面核心区域之内。
9.3 弯曲与扭转的组合弯曲与扭转组合变形是机械工程中常见的情况。
以图9.6所示一端固定的曲拐为例,说明弯曲与扭转组合变形的强度计算方法。
设拐轴AB 段为等圆杆,直径为d ,A 端为固定端约束。