机械振动简谐振动仿真
- 格式:docx
- 大小:2.30 MB
- 文档页数:43

《机械振动“简谐运动”》教学设计与反思刘志坚一、教学设计教学目的:1、知道机械振动是物体机械运动的另一种形式,知道机械振动的概念;2、知道什么是简谐运动,理解简谐运动回复力的特点;3、理解简谐运动中各物理量的变化情况;教学重点:1、简谐运动的定义,2、培养学生的观察能力、逻辑思维能力和实践能力。
教学难点:简谐运动的回复力特征。
教学用具:弹簧振子、单摆、摆钟、一端夹紧的钢条、音叉课件:PPt文稿(带Flash动画)教学过程:1、提问:到目前为止,大家所了解的机械运动有哪几种?(匀速直线运动,匀变速直线运动、平抛运动、匀速圆周运动……)。
2、学生观察实验、动画。
并说说是什么样的机械运动。
演示:单摆、竖直弹簧下的钩码的振动。
动画:钟摆,荡秋千,思考:这些运动与我们以前了解的运动相比有什么区别?——往复运动引出“机械振动”概念。
动画举例:衣物在微风中的摇摆,木板的颤动、人走路时手臂的摆动,地震。
3、思考:物体为什么会做往复运动呢?物理学对物体运动的研究:(1)受力特征;(2)运动规律。
物体做机械运动时,受力有何特征?运动规律怎样?学生继续观察演示和动画,然后讨论机械振动的受力特征——明确:物体一旦离开平衡位置,就会受到一个指向平衡位置的力的作用。
引出“回复力”概念:4、教师讲述:从今天开始,我们来了解机械振动的一些最基本的知识。
研究振动也从最简单、最基本的振动着手,这种振动叫简谐运动。
演示:气垫弹簧振子的运动。
引出理想模型:弹簧振子:在忽略摩擦和空气阻力以及弹簧质量的情况下,小球和弹簧组成的系统。
5、弹簧振子的运动是机械振动,必定受到回复力作用。
请注意观察振子的运动,思考:是什么力在充当回复力呢?这个力的大小和方向有什么特点呢?请大家分组讨论,填写思考题。
思考题:振子由A向O运动时,弹簧弹力的方向指向__O__点;振子由O向A‘运动时,弹簧弹力的方向指向 O 点;振子由A’向O运动时,弹簧弹力的方向指向 O 点;振子由O向A运动时,弹簧弹力的方向指向 O 点;根据胡克定律,弹簧弹力的大小F= kx 。

物理机械振动、简谐振动图像讲解物理机械振动、简谐振动图像讲解一. 本周教学内容:机械振动、简谐振动图像二. 总结归纳知识网络:三. 重、难点分析1. 描述振动的量(1)位移x:由平衡位置指向振动质点所在位置的有向线段,矢量。
(2)振幅A:振动离开平衡位置的最大距离,标量,表示振动的强弱。
(3)周期T和频率f:物体完成一次全振动所需的时间叫周期,而频率那么等于单位时间内完成全振动的次数,它们是表示振动快慢的物理量,二者互为倒数关系: < "0" 1248287925"> 其中摆长4. 简谐运动的图象(1)如下图为一弹簧振子做简谐运动的图象,它反映了振子的位移随时间变化的规律,而其轨迹并非正弦曲线。
(2)根据简谐运动的规律,利用该图象可以得出以下信息:1°振幅A、周期T以及各时刻振子的位置。
2°各时刻回复力、加速度、速度、位移的方向。
3°某段时间内位移、回复力、加速度、速度、动能、势能的变化情况。
4°某段时间内振子的路程。
5. 振动的类型(1)简谐运动(又称自由振动):机械能守恒,振幅不变,周期等于固有周期。
(2)阻尼振动:系统机械能不断损耗,振幅不断减小,周期等于固有周期。
(3)受迫振动:物体在周期性驱动力作用下的振动,振动稳定后的频率等于驱动力的频率,与物体的固有频率无关。
(4)共振:当驱动力的频率跟物体的固有频率相等时的受迫振动,振幅最大。
【典型例题】例1. (1998年?全国)如下图,两单摆摆长相同,平衡时两摆球刚好接触。
现将摆球A在两摆球线所在平面内向左拉开一小角度释放,碰撞后,两摆球分开各自做简谐运动,以mA、mB分别表示摆球A、B的质量,那么()A. 如果mA>mB,下一次碰撞将发生在平衡位置右侧B. 如果mAC. 无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置右侧D. 无论两摆球的质量之比是多少,下一次碰撞都不可能在平衡位置左侧解析:碰撞后两球各自做简谐运动,两摆的摆长相等,周期的大小与振幅、质量无关,两摆的周期相等。
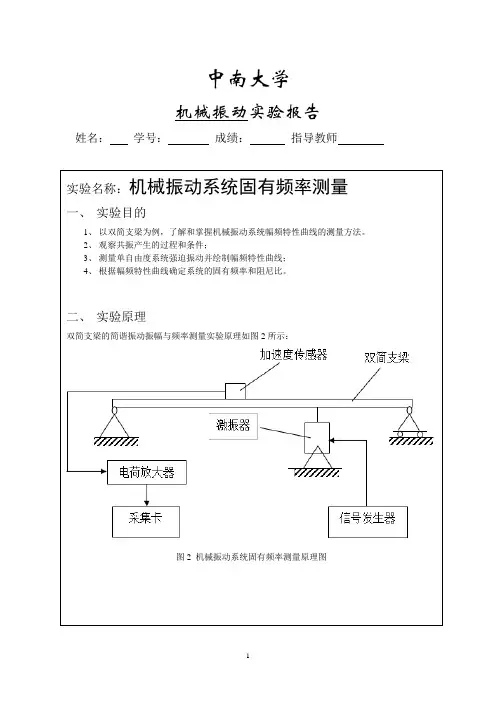

机械振动实验报告1. 实验目的本实验旨在通过对机械振动的实验研究,掌握机械振动的基本原理和特性,深入了解振动系统的参数对振动现象的影响。
2. 实验原理(1)简谐振动:当物体在受到外力作用下,沿着某一方向做来回运动时,称为简谐振动。
其数学表达式为x(t) = A*sin(ωt + φ),其中A 为振幅,ω为角频率,φ为初相位。
(2)受迫振动:在外力的作用下振动的振幅不断受到调节,导致振幅和相位角与外力作用间存在一定的关联关系。
(3)自由振动:在无外力作用下,振动系统的振幅呈指数幅度减小的振动现象。
3. 实验内容(1)测量弹簧振子的简谐振动周期并绘制振幅-周期曲线。
(2)通过改变绳长和质量对受迫振动的谐振频率进行测量。
(3)观察受外力激励时的自由振动现象。
4. 实验数据与结果(1)弹簧振子简谐振动周期测量结果如下:振幅(cm)周期(s)0.5 0.81.0 1.21.5 1.62.0 1.9(2)受迫振动的谐振频率测量结果如下:绳长(m)质量(kg)谐振频率(Hz)0.5 0.1 2.50.6 0.2 2.00.7 0.3 1.80.8 0.4 1.5(3)外力激励下的自由振动现象结果呈现出振幅逐渐减小的趋势。
5. 实验分析通过实验数据处理和结果分析,可以得出以下结论:(1)弹簧振子的振动周期与振幅呈线性关系,在一定范围内,振幅增大,周期相应增多。
(2)受迫振动的谐振频率随绳长和质量的增加而减小,表明振动系统的参数对谐振频率有一定的影响。
(3)外力激励下的自由振动现象符合指数幅度减小的规律,振幅随时间的增长呈现递减趋势。
6. 实验总结本实验通过测量和观察机械振动的不同现象,探究了振动系统的基本原理和特性。
实验结果表明振动系统的参数对振动现象产生了明显的影响,为进一步深入研究振动学提供了基础。
通过本次实验,我对机械振动的原理和特性有了更深入的了解,对实验数据处理和分析方法也有了更加熟练的掌握。
希望通过不断的实验学习,能够进一步提升自己对振动学理论的理解水平,为未来的科研工作打下坚实基础。


机械振动-简谐振动-弹簧振子机械振动的定义机械振动是指物体或质点在其平衡位置附近所作有规律的往复性运动。
老式的钟表,下面都有一个钟摆,钟摆的左右摆动,就是一种机械振动。
另外,单摆也是一种典型的机械振动。
常用来描述机械振动的物理量是位移、速度、加速度、力、周期、频率。
机械振动典型案例高中物理选修3-4教材中主要讨论了两个机械振动的模型,其一是弹簧振子,其二是单摆。
这两种振动模式都属于简谐振动(简谐振动定义在文章下方)。
下面分别对这两种机械振动模式进行简要介绍。
1.弹簧振子弹簧振子是一个不考虑摩擦阻力,不考虑弹簧的质量,不考虑振子的大小和形状的理想化的物理模型。
如下图所示,不考虑小球与桌面的摩擦以及弹簧的质量,初始时刻小球在弹簧原长位置获得一定速度,则小球会在弹簧弹力的作用下,以O点为中心往复运动。
这就是弹簧振子模型。
2.单摆单摆是一种理想的物理模型,它由理想化的摆球和摆线组成。
如下图所示,不计摆线的伸缩和空气摩擦,当把小球拉离到某一位置(摆线与竖直方向夹角为θ,要求θ小于5°),则小球会周而复始的做往复运动。
这就是单摆模型。
单摆的周期与摆线长度和当地重力加速度有关,我们可以利用单摆来测定当地重力加速度。
机械振动分类从高中物理考题来看,机械振动分类可分为:简谐振动与非简谐振动。
简谐振动指的是满足,物体所受的力跟位移成正比,并且力总是指向平衡位置。
我们把物体所受到的力称之为回复力。
如果用F表示物体受到的回复力,用x表示小球对于平衡位置的位移,根据胡克定律,F和x成正比,它们之间的关系可用下式来表示:F=-kx;请注意,这里的负号指的是方向,因为回复力的方向,总是与物体运动的位移方向相反。
简谐振动是一种没有能量损失的振动模式,在没有外界干扰下,将永远运动下去。
非简谐振动也可称之为阻尼振动,指的是由外在阻力作用,这种机械振动模式早晚会停下来。
简谐振动简谐振动指的是满足,物体所受的力跟位移成正比(F=-kx),并且力总是指向平衡位置。


机械振动与简谐运动的关系1. 前言嗨,朋友们,今天咱们来聊聊一个听上去有点高深,但其实特别有趣的话题——机械振动和简谐运动的关系。
别担心,咱们不会用什么高大上的专业术语,而是用最简单的语言来捋一捋这两个概念之间的关系。
就像一杯热腾腾的奶茶,暖心又简单。
要知道,这两者的关系就像是老友记里的那些角色,互相依赖、互相影响,缺一不可。
2. 机械振动:动起来的感觉2.1 机械振动的基本概念首先,我们得弄清楚什么是机械振动。
简单来说,机械振动就是物体在平衡位置附近来回摆动的现象。
你想象一下,一个秋千,风一吹,它就摇摇晃晃,正好是机械振动的经典案例。
就像人们在公园里,坐在秋千上,嬉笑打闹,感觉仿佛时间都停了。
哈哈,虽然摇得晕头转向,但这就是振动的魅力。
2.2 机械振动的例子再举个例子,想想一根琴弦。
当你拨动它的时候,琴弦就开始振动,发出悦耳的音符。
其实,机械振动无处不在,从你每天走路时脚步的节奏,到你敲桌子时的节拍,都是在演绎着振动的精彩。
没错,振动就是这么普遍,像是生活中的调味品,给我们带来各种各样的感觉。
3. 简谐运动:有规律的舞蹈3.1 简谐运动的基本概念那么,简谐运动又是个啥呢?它是一种特殊的机械振动。
简单来说,简谐运动就是物体在某个平衡位置附近,以固定的频率和幅度来回摆动的运动。
你可以把它想象成一个人正在跳舞,随着音乐的节拍而摇摆,既有节奏又有韵律,动得恰到好处,简直就是优雅的化身。
3.2 简谐运动的特点而且,简谐运动的一个特点就是它的规律性。
它像个守时的小伙伴,每次摆动的时间都是一样的,简直让人想起了那些一丝不苟的钟表。
你想,如果时间一直乱七八糟,那生活该多混乱呀!所以,简谐运动的规律性让我们的世界变得有序,真是不可或缺。
4. 机械振动与简谐运动的关系4.1 它们之间的联系好了,接下来咱们聊聊机械振动和简谐运动的关系。
其实,简谐运动可以看作是机械振动中的一员,或者说是“精英”。
换句话说,并不是所有的机械振动都是简谐运动,但所有的简谐运动都是机械振动。


仿真震动频率如何计算公式引言。
在工程和科学领域中,震动频率是一个非常重要的参数,它可以用来描述物体在振动过程中的频率和周期。
在仿真和模拟实验中,计算震动频率是十分必要的,因为它可以帮助工程师和科学家更好地了解物体的振动特性,从而进行合理的设计和分析。
本文将介绍如何计算仿真震动频率的公式,并探讨一些相关的实际应用。
一、简介。
在物体振动的过程中,震动频率是指单位时间内振动的次数,通常用赫兹(Hz)作为单位。
震动频率与振动周期之间有着密切的关系,振动周期是指一个完整的振动循环所需要的时间,它与震动频率的倒数成正比。
因此,震动频率和振动周期是可以相互转换的。
在实际的工程和科学应用中,我们通常会遇到需要计算震动频率的情况,比如在振动传感器设计、机械振动分析、声学工程等领域。
二、计算公式。
在进行仿真和模拟实验时,计算震动频率的公式可以根据具体的振动系统和振动类型来确定。
一般来说,对于简单的单自由度振动系统,可以使用以下的公式来计算震动频率:f = 1/2π√(k/m)。
其中,f表示震动频率,k表示系统的刚度,m表示系统的质量。
这个公式是根据简谐振动的特性推导出来的,它描述了系统的固有频率与系统的质量和刚度之间的关系。
在实际的工程设计和分析中,可以通过测量系统的质量和刚度来计算系统的固有频率,从而得到系统的震动频率。
对于复杂的多自由度振动系统,可以使用有限元分析等方法来计算系统的固有频率和震动频率。
有限元分析是一种常用的工程仿真方法,它可以通过离散化系统的结构和材料来计算系统的固有频率和模态形式,从而得到系统的震动频率。
有限元分析可以有效地模拟复杂的振动系统,比如机械结构、建筑物、汽车、飞机等,从而帮助工程师和科学家更好地了解系统的振动特性。
三、实际应用。
计算震动频率的公式在工程和科学领域中有着广泛的应用,下面将介绍一些实际的应用案例。
1. 振动传感器设计。
在振动传感器的设计中,需要计算传感器的固有频率和灵敏度,以确保传感器可以有效地检测系统的振动。
第四讲 机械振动1 .简谐振动的受力分析2 .等效法研究简谐振动3 .三角函数法描述振动第一部分:振动的受力特点以及参数知识点睛 一、模型引入 1.什么是振动?振动是自然界和工程技术领域常见的一种运动,广泛存在于机械运动、电磁运动、热运动、原子运动等运动形式之中.从狭义上说,通常把具有时间周期性的运动称为振动.如钟摆、发声体、开动的机器、行驶中的交通工具都有机械振动.如图:振动演示实验:当振子往复振动时,匀速的拉动纸带,就可以研究振子离开中心位置的位移与时间的关系。
广义地说,任何一个物理量在某一数值附近作周期性的变化,都称为振动.变化的物理量称为振动量,它可以是力学量,电学量或其它物理量.例如:交流电压、电流的变化、无线电波电磁场的变化等等.2.什么是机械振动?机械振动是最直观的振动,它是物体在一定位置附近的来回往复的运动,口语称为“来回晃悠”。
如活塞的运动,钟摆的摆动等都是机械振动.产生机械振动的条件是:物体受到回复力的作用; 回复力:使振动物体返回平衡位置的力叫回复力.回复力时刻指向平衡位置.回复力是以效果命名的力,它是振动物体在振动方向上的合外力,可能是几个力的合力,也可能是某个力或某个力的分力,可能是重力、弹力、摩擦力、电场力、磁场力等.3.简谐运动物体在跟偏离平衡位置的位移大小成正比,并且总指向平衡位置的回复力作用下的振动,叫简谐运动.表达式为:F kx =-.做简谐运动物体的位移是相对于平衡位置的,位移的方向总是由平衡位置指向物体,而回复力总由物体是指向平衡位置,所以回复力总跟位移方向相反,式中的负号表示了这种相反关系. 4.描述简谐运动的物理量⑴ 位移x :由平衡位置指向振子所在处的有向线段,最大值等于振幅;知识模块本讲介绍⑵ 振幅A :是描述振动强弱的物理量.(一定要将振幅跟位移相区别,在简谐运动的振动过程中,振幅是不变的,而位移是时刻在改变的)⑶ 周期T :是描述振动快慢的物理量.频率1f T=.5.简谐振动的图像为了研究弹簧振子的运动规律,我们以小球的平衡位置为坐标原点O ,沿着它的振动方向建立坐标轴.小球在平衡位置的右边时它对平衡位置的位移为正,在左边时为负.左图所示的弹簧振子的频闪照片.频闪仪每隔0.05s 闪光一次,闪光的瞬间振子被照亮.拍摄时底片从下向上匀速运动,因此在底片上留下了小球和弹簧的一系列的像,相邻两个像之间相隔0.05s .右图中的两个坐标轴分别代表时间t 和小球位移x ,因此它就是小球在平衡位置附近往复运动时的位移—时间图象,即x t -图象.简谐运动及其图象我们对弹簧振子的位移与时间的关系做些深入的研究.从图中可以看出,小球运动时位移与时间的关系很像正弦函数的关系.例题精讲【例1】 如图所示,质量为m 的小球放在劲度为k 的轻弹簧上,使小球上下振动而又始终未脱离弹簧,证明其做简谐振动.【例2】 把一个密度小于水的正方体木块放入水中,并用手稍微按入水中一点,证明手释放后木块做简谐振动,不考虑阻力与水面的变化.【解析】 设物体相对飘浮位置位移x .其受合力为相比飘浮时的浮力差.F g V ρ∆=∆浮水gS x ρ=⋅浮K gS ρ=水【例3】 三根长度均为 2.00l =米,质量均匀的直杆,构成一正三角形框架ABC .C 点悬挂在一光滑水平转轴上,整个框架可绕转轴转动.杆AB 是一导轨,一电动玩具松鼠可在导轨上运动,如图所示.现观察到松鼠正在导轨上运动,而框架却静止不动,试论证松鼠的运动是一种什么样的运动.【解析】 如图,松鼠受力如图:由力矩平衡可知:N 与f 合力必须过ABC框的C 点才能平衡. 即Nx fh =,且N mg =∴mgx f h=为简谐振动.且mgK h=.第二部分 简谐振动参量关系:知识点睛由于是变力作用,所以简谐振动的物体运动量与时间的关系很难用初等数学解答,一般的解法是直接解微分方程.根据牛顿第二定律: f ma =可得物体的加速度为:f ka x m m==-对于给定的弹簧振子,m 和k 均为正值常量,令2kmω=则上式可以改写为 2a x ω=-或2220d x x dtω+=这是个二阶的微分方程,这里就给出具体解的过程了。
《机械振动“简谐运动”》教学设计与反思刘志坚一、教学设计教学目的:1、知道机械振动是物体机械运动的另一种形式,知道机械振动的概念;2、知道什么是简谐运动,理解简谐运动回复力的特点;3、理解简谐运动中各物理量的变化情况;教学重点:1、简谐运动的定义,2、培养学生的观察能力、逻辑思维能力和实践能力。
教学难点:简谐运动的回复力特征。
教学用具:弹簧振子、单摆、摆钟、一端夹紧的钢条、音叉课件:PPt文稿(带Flash动画)教学过程:1、提问:到目前为止,大家所了解的机械运动有哪几种?(匀速直线运动,匀变速直线运动、平抛运动、匀速圆周运动……)。
2、学生观察实验、动画。
并说说是什么样的机械运动。
演示:单摆、竖直弹簧下的钩码的振动。
动画:钟摆,荡秋千,思考:这些运动与我们以前了解的运动相比有什么区别?——往复运动引出“机械振动”概念。
动画举例:衣物在微风中的摇摆,木板的颤动、人走路时手臂的摆动,地震。
3、思考:物体为什么会做往复运动呢?物理学对物体运动的研究:(1)受力特征;(2)运动规律。
物体做机械运动时,受力有何特征?运动规律怎样?学生继续观察演示和动画,然后讨论机械振动的受力特征——明确:物体一旦离开平衡位置,就会受到一个指向平衡位置的力的作用。
引出“回复力”概念:4、教师讲述:从今天开始,我们来了解机械振动的一些最基本的知识。
研究振动也从最简单、最基本的振动着手,这种振动叫简谐运动。
演示:气垫弹簧振子的运动。
引出理想模型:弹簧振子:在忽略摩擦和空气阻力以及弹簧质量的情况下,小球和弹簧组成的系统。
5、弹簧振子的运动是机械振动,必定受到回复力作用。
请注意观察振子的运动,思考:是什么力在充当回复力呢?这个力的大小和方向有什么特点呢?请大家分组讨论,填写思考题。
思考题:振子由A向O运动时,弹簧弹力的方向指向__O__点;振子由O向A‘运动时,弹簧弹力的方向指向 O 点;振子由A’向O运动时,弹簧弹力的方向指向 O 点;振子由O向A运动时,弹簧弹力的方向指向 O 点;根据胡克定律,弹簧弹力的大小F= kx 。
摘要机械振动主要有简谐振动,阻尼振动,受迫振动三种。
对三种振动建立模型,列出振动方程,再对三种振动给定初始条件,就可以利用Matlab Simulink功能对三种振动进行仿真模拟,得出振动的位移,速度,加速度,动能,势能,机械能随时间的变化关系图像。
另外,我们对振动方程求解,得出振子位移关于时间的函数,再分别对其求一阶、二阶导数,就可以得出速度、加速度函数,再经过简单运算就可以得到动能、势能、机械能函数。
我们再通过分析函数来分析其图像,再对比仿真模拟出的图像,就可以确定我们的仿真研究方法的可信度。
关键词:简谐振动;阻尼振动;受迫振动;共振1引言——机械振动的仿真原理1.1 Matlab Simulink功能简述Simulink是基于Matlab的框图设计环境,可以用来对各种动态系统进行建模、分析和仿真,它的建模范围广泛,可以针对任何能用数学来描述的系统进行建模,例如航空航天动力学系统、卫星控制制导系统、通信系统、船舶及汽车等,其中包括了连续、离散,条件执行,事件驱动,单速率、多速率和混杂系统等。
Simulink提供了利用鼠标拖放的方法来建立系统框图模型的图形界面,而且还提供了丰富的功能块以及不同的专业模块集合,利用Simulink几乎可以做到不书写一行代码即完成整个动态系统的建模工作。
除此之外,Simulink还支持Stateflow,用来仿真事件驱动过程。
Simulink是从底层开发的一个完整的仿真环境和图形界面,是模块化了的编程工具,它把Matlab的许多功能都设计成一个个直观的功能模块,把需要的功能模块用连线连起来就可以实现需要的仿真功能了。
也可以根据自己的需要设计自己的功能模块,Simulink功能强大,界面友好,是一种很不错的仿真工具[1]。
1.2机械振动的物理模型物理学中的机械振动主要分为简谐振动、阻尼振动、受迫振动三种。
下面我们根据这三种类型的振动建立物理模型来分别研究。
1.2.1简谐振动的物理模型图1 弹簧振子做简谐振动物理实验模型如上图所示,弹簧振子在O 附近做简谐振动。
摘要机械振动主要有简谐振动,阻尼振动,受迫振动三种。
对三种振动建立模型,列出振动方程,再对三种振动给定初始条件,就可以利用Matlab Simulink功能对三种振动进行仿真模拟,得出振动的位移,速度,加速度,动能,势能,机械能随时间的变化关系图像。
另外,我们对振动方程求解,得出振子位移关于时间的函数,再分别对其求一阶、二阶导数,就可以得出速度、加速度函数,再经过简单运算就可以得到动能、势能、机械能函数。
我们再通过分析函数来分析其图像,再对比仿真模拟出的图像,就可以确定我们的仿真研究方法的可信度。
关键词:简谐振动;阻尼振动;受迫振动;共振1引言——机械振动的仿真原理1.1 Matlab Simulink功能简述Simulink是基于Matlab的框图设计环境,可以用来对各种动态系统进行建模、分析和仿真,它的建模范围广泛,可以针对任何能用数学来描述的系统进行建模,例如航空航天动力学系统、卫星控制制导系统、通信系统、船舶及汽车等,其中包括了连续、离散,条件执行,事件驱动,单速率、多速率和混杂系统等。
Simulink提供了利用鼠标拖放的方法来建立系统框图模型的图形界面,而且还提供了丰富的功能块以及不同的专业模块集合,利用Simulink几乎可以做到不书写一行代码即完成整个动态系统的建模工作。
除此之外,Simulink还支持Stateflow,用来仿真事件驱动过程。
Simulink是从底层开发的一个完整的仿真环境和图形界面,是模块化了的编程工具,它把Matlab的许多功能都设计成一个个直观的功能模块,把需要的功能模块用连线连起来就可以实现需要的仿真功能了。
也可以根据自己的需要设计自己的功能模块,Simulink功能强大,界面友好,是一种很不错的仿真工具[1]。
1.2机械振动的物理模型物理学中的机械振动主要分为简谐振动、阻尼振动、受迫振动三种。
下面我们根据这三种类型的振动建立物理模型来分别研究。
1.2.1简谐振动的物理模型图1 弹簧振子做简谐振动物理实验模型如上图所示,弹簧振子在O 附近做简谐振动。
已知弹簧振子质量为m ,所受合力为F ,弹簧劲度系数为k ,则有:F kx =-。
又由牛顿第二定律有:22d xF ma m dt== (1)于是可以得到: 220d x kx dt m+=(2)令m k =2ω,则可得: 2220d xx dtω+= (3)方程(3)的解x 即为弹簧振子在时刻t 时的振动位移,一阶导数x 即为弹簧振子在时刻t 时振动速度,其二阶导数x 即为弹簧振子在时刻t 时的加速度。
1.2.2阻尼振动的物理模型如图1,若弹簧振子在x 轴上受到粘滞阻尼的作用力,则弹簧振子做阻尼的振动。
设弹簧振子受到的阻尼力为:dxf v dtγγ=-=- (4) 式中γ 为阻尼系数,与物体的形状以及周围性质有关。
弹簧振子受到的弹力为F kx =-,则对弹簧振子,有牛顿第二定律有:22d d d d x xm kx t tγ=-- (5) 整理后得: 22d d d d x k xx t m m tγ=--(6)令2k m ω=,2n mγ=,则有: 2202d d 20d d x x n x t tω++=(7)这就是阻尼振动的振动方程。
其解x 即为弹簧振子在时刻t 时的振动位移,一阶导数x即为弹簧振子在时刻t 时振动速度,其二阶导数x 即为弹簧振子在时刻t 时的加速度。
1.2.3受迫振动的物理模型如图2,弹簧振子在O 附近做阻尼振动。
已知弹簧振子质量为m ,弹簧劲度系数为k 。
平行于x 轴的平面对弹簧振子有阻尼力的作用。
对弹簧振子施加一外加激励力()f t ,设0()sin f t F t ω=,则称为谐激励力,其中ω为外施激励频率,t 是持续时间。
对弹簧振子受力分析,其所受弹力为:F kx =-。
由于阻尼振动是振幅(或能量)随时间不断减少的振动。
能量减少的原因是有粘滞阻尼和辐射阻尼。
为方便,均视为粘滞阻尼。
则弹簧图2 弹簧振子在外加激励力作用下做阻尼受迫振动振子所受阻尼力为:dxf v dtγγ=-=- (8) 式中γ 为阻尼系数,与物体的形状以及周围性质有关。
则对弹簧振子,由牛顿第二定律有:202sin d x dx m kx F t dt dtγω=--+ (9) 对(9)式变形可得:202sin F d x k dx x t dt m m dt mγω=--+ (10) 令00,2,F k n h m m mγω===,0ω为固有频率,n 为阻尼因数,则(10)可变为: 22022sin d x dxn x h t dt dtωω++= (11)方程(11)的解就是时刻t 时弹簧振子的位移,其一阶导数x 即为弹簧振子在时刻t 时振动速度,其二阶导数x 即为弹簧振子在时刻t 时的加速度[2]。
我们记0/n ξω=为相对阻尼系数或阻尼比。
根据阻尼对系统振动的影响,振动响应分为弱阻尼(ξ<1)、强阻尼(ξ>1)和临界阻尼(ξ=1)三种情况,这里仅讨论弱阻尼的情况。
1.3 Matlab Simulink 仿真原理简述在得到弹簧振子的简谐振动、阻尼振动和受迫振动方程后,通过这三个方程,我们可以用高等数学的方法求出这三个方程的通解。
同时,我们可以用Matlab 的计算功能求出它们的通解。
这三个方程的通解表示振子位移随时间的变化情况。
我们得到的这三个方程,前两个为二阶常系数线性齐次微分方程,第三个为二阶常系数非齐次微分方程。
根据这三个方程,我们可以通过Matlab Simulink 中的各种模块模拟弹簧振子的位移、速度、加速度,再添加一个平方模块,设置好系数,就可以模拟振子动能、势能、机械能,用线连接各模块,这样流程图就做好了。
设置好各模块的参数后,再设置好系统环境变量,点击运行,通过示波器模块就可以模拟出相应的图像曲线[3]。
图像的横坐标均表示时间,纵坐标相应为位移、速度、加速度、动能、势能、机械能。
图像表示这些物理量随时间变化关系。
通过这三种情况方程的通解,我们可以分析振子位移随时间变化情况,再和模拟出的图像对比分析。
对方程通解求一阶导,就可以得到振子速度随时间变化关系,分析出速度随时间变化情况,再和模拟出的图像对比分析。
同样我们可以求出方程通解的二阶导数,这就是振子加速度随时间变化关系,分析函数特征,再和模拟出的函数图像对比分析,就可以分析模拟出的图像是否正确,及其与理论符合情况。
2简谐振动方程的解及其模拟仿真2.1简谐振动方程的求解这里,我们设系统初始条件为0t =s 时,04m x =,00m/s v =。
通过高等数学方法解这个齐次微分方程可得:12cos sin )cos()x C t C t t A t ωωωϕωϕ=+=+=+ (12)式中21tan ,C A C ϕ=-。
则速度表达式为:sin()v x A t ωωϕ==-+,将初始条件代入(12)式,可得:4cos()x t ωϕ=+ (13)这就是满足初始条件的简谐振动方程的解。
由(13)式我们可以得出弹簧振子位移随时间的变化情况。
振子周期为2T πω=。
0s t =时,振子位移正向最大位移出,即图1中的A 位置,此时振子速度为0,加速度最大;经4T,振子向负方向运动到平衡位置,此时振子速度最大,加速度为0;再经4T,振子继续向负方向运动到负的最大位移处,此时速度为0,加速度最大;再经过4T,振子向正向运动到平衡位置,此时速度最大,加速度为0;最后经过4T,振子回到初始位置,即正的最大位移处,完成一个周期的振动。
通过matlab7.0符号运算,可以得出该微分方程的解,相关程序见附录程序1。
2.2简谐振动模型的仿真研究 2.2.1基本模型的建立我们设系统的固有频率1ω-=,则2200.5s ω-=。
于是(3)式变为:220.50d xx dt +=。
打开Simulink Library Browser ,选择新建按钮,根据所需要模拟的运动方程选取模块,其中包括Subtract、Intergrator、Gain以及Scope 模块,需要注意的是将Subtract模块中的List of signs改为--,以便让x前面的符号为负,为了使x前的系数为0.5,将Gainl中的值设为0.5,速度项系数Gain设为0。
设置位移模块的初始值为4,速度模块的初始值设为0,加速度模块的初始值设为0。
这样,几个关键模块的属性就根据方程的需要设置好了。
(1)运用Gain1将x和0.5相乘。
(2)运用Subtract使x前面的符号为负。
(3)运用Intergrator将x积分为x,将x积分为x。
Scope为示波器输出模块。
最后,将各个模块按照方程的需要逐一连接,如图3所示[4]。
图3简谐振动位移仿真模拟流程图图4简谐振动位移仿真模拟图像单击右键,选择Configuration Parameters设置系统的运行环境,初始运行时间设为0s,停止时间取为80s,最大步长设为0.1,初始步长设为0.01,设好后,点击OK。
再点击图3“Scope”输出模块得到振子位移仿真曲线如图4所示。
图中横坐标表示时间,单位为s,纵坐标表示位移,单位为m。
2.2.2 速度、加速度的监测要得到速度与加速度的实时振动曲线只需要在图3的基础上加入两个Scope 模块,如图5所示。
图5弹簧振子速度、加速度仿真模拟流程图运行Scope1得到弹簧振子速度图像,如图6所示。
图中横坐标表示时间,单位为s,纵坐标表示振子速度,单位为m/s。
图6 弹簧振子速度仿真模拟图像 图7 弹簧振子加速度仿真模拟图像运行Scope2,就得到弹簧振子加速度监测图像,如图7所示。
图中横坐标表示时间,单位为s ,纵坐标表示振子加速度,单位为2m/s 。
2.2.3 动能、势能、机械能监测系统动能、势能、机械能的定义如下:212k E mv = (14) 212p E kx =(15) p k t E E E += (16) 根据动能与势能的公式在原有的简谐振动模拟流程图中加入Product 模块(实现2x 和2v 运算)和增益模块Gain 以及Sum 模块将两输入信号进行叠加便可将动能与势能及机械能波形输出出来。
先对各个模块名进行编辑,设置好字体大小,再进行各个模块的属性设定。
前面我们已经设定了x 的系数即Gain1参数为0.5,即:0.5k m =,这里,我们取1k g m =,则0.5N/m k =。
我们由此可得到动能中速度的平方项系数20.5m =,即Gain2参数为0.5;势能中x 平方项系数20.25k =,即Gain3的参数为0.25。
最后用仿真信号线将各个模块连接起来,如下图8所示[5]。
图8 简谐振动弹簧振子动能、势能、机械能流程图单击运行后,点击“t E ”输出模块得到总能量曲线,点击“k E ”输出模块得到动能曲线,点击“p E ”输出模块得到势能曲线如图9,图10,图11所示,图中横坐标代表时间,单位为s ,纵坐标分别代表动能、势能、机械能,单位为J 。