第五章 位移法
- 格式:ppt
- 大小:1.01 MB
- 文档页数:29


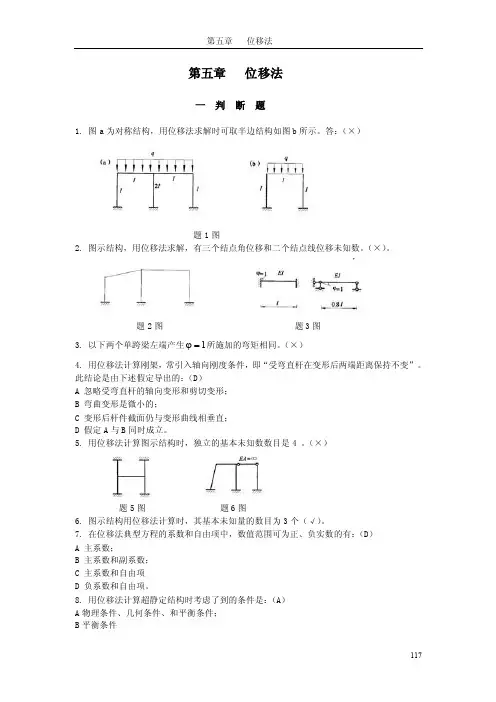
第五章位移法一判断题1. 图a为对称结构,用位移法求解时可取半边结构如图b所示。
答:(×)题1图2. 图示结构,用位移法求解,有三个结点角位移和二个结点线位移未知数。
(×)。
题2图题3图ϕ=所施加的弯矩相同。
(×)3. 以下两个单跨梁左端产生14. 用位移法计算刚架,常引入轴向刚度条件,即“受弯直杆在变形后两端距离保持不变”。
此结论是由下述假定导出的:(D)A 忽略受弯直杆的轴向变形和剪切变形;B 弯曲变形是微小的;C 变形后杆件截面仍与变形曲线相垂直;D 假定A与B同时成立。
5. 用位移法计算图示结构时,独立的基本未知数数目是4 。
(×)题5图题6图6. 图示结构用位移法计算时,其基本未知量的数目为3个(√)。
7. 在位移法典型方程的系数和自由项中,数值范围可为正、负实数的有:(D)A 主系数;B 主系数和副系数;C 主系数和自由项D 负系数和自由项。
8. 用位移法计算超静定结构时考虑了到的条件是:(A)A物理条件、几何条件、和平衡条件;B平衡条件117C平衡条件与物理条件D平衡条件与几何条件9. 规定位移法的杆端弯矩正负时,对杆端而言,以顺时针为正,对结点则以逆时针为正,这一规定也适合于杆端剪力的符号规定。
(×)10. 图a对称结构可简化为图(b)来计算。
(×)题10图题11图11. 图示结构用位移法求解时,基本未知量个数是相同的(√)12. 图示结构用位移法求解时,只有一个未知数(√)题12图题13图题14图13. 图示结构横梁无弯曲变形,故其上无弯矩。
(×)14. 图a对称结构可简化为图b来计算,EI均为常数。
(×)15. 图示结构用位移法求解的基本未知量数目最少为3。
(√)题15图题16图16. 图示结构EI=常数,用位移法求解时有一个基本未知量。
(√)。
17. 位移法中固端弯矩是当其基本未知量为零时由外界因数所产生的杆端弯矩(√)18. 位移法的典型方程与力法的典型方程一样,都是变形协调方程。




位移法的知识点总结一、基本原理1. 位移法的基本原理位移法是以位移为基本变量进行分析的一种结构分析方法。
它的基本原理是根据结构受力状态和边界条件,通过对结构各部分的变形进行分析,推导出结构的位移场。
根据结构力学的基本原理,结构的受力和变形是密切相关的,因此通过分析结构的位移场,可以获得结构的受力分布和变形情况,为结构的设计和分析提供重要参考。
2. 位移的重要性在结构力学中,位移是描述结构变形的基本形式之一,它直接反映了结构受力的情况。
在进行结构分析时,通常可以通过计算结构的位移场来获得结构的受力分布和变形情况。
因此,位移是结构分析的重要变量,在位移法中被广泛应用。
3. 位移法的实质位移法的实质是通过假设结构各部分的变形是线性的,即受到外力作用后,结构的变形与受力成线性关系。
这一假设是位移法能够简化结构分析的基础,使得结构分析更加方便和实用。
二、应用范围1. 适用范围位移法适用于各种类型的结构,包括梁、柱、板、桁架、壳体等。
它可以用于解决结构在受力作用下的位移和变形问题,对于复杂结构的受力分析和设计具有广泛的适用性。
2. 适用条件位移法的应用条件包括结构受力状态和边界条件的明确,结构各部分的变形可线性假设,结构受力和变形之间存在较强的相关性等。
在满足这些条件的情况下,位移法可以有效地用于解决各种结构受力和变形问题。
三、操作步骤1. 结构建模首先需要对结构进行建模,确定结构的几何形状、受力条件和边界条件等。
通过建模可以获得结构的刚度矩阵和载荷向量,为后续的分析提供基础数据。
2. 变形分析根据结构的刚度矩阵和载荷向量,可以建立结构的位移方程。
通过对位移方程进行分析,可以获得结构的位移场,揭示结构受力和变形的关系。
3. 反演求解根据结构的位移场,可以反演求解结构的受力分布和变形情况。
通过求解可以获得结构各部分的受力情况,评估结构的受力状况和安全性。
4. 结果分析最后需要对求解结果进行分析,评估结构的受力和变形情况。

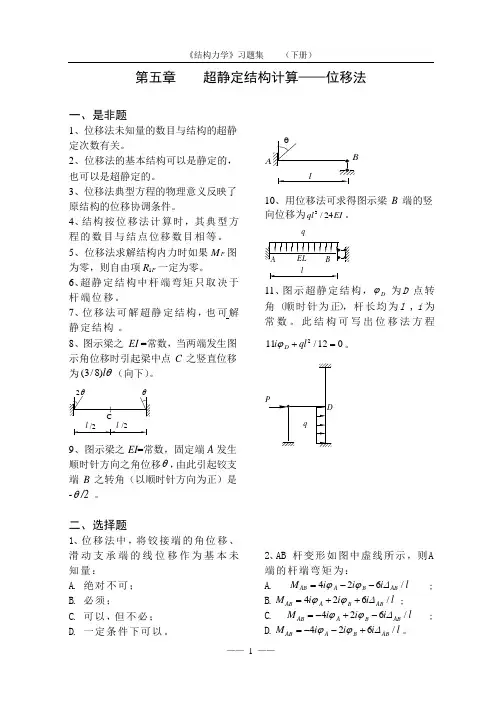
第五章 超静定结构计算——位移法一、是非题1、位移法未知量的数目与结构的超静定次数有关。
2、位移法的基本结构可以是静定的,也可以是超静定的。
3、位移法典型方程的物理意义反映了原结构的位移协调条件。
4、结 构 按 位 移 法 计 算 时 , 其 典 型 方 程 的 数 目 与 结 点 位 移 数 目 相 等 。
5、位移法求解结构内力时如果P M 图为零,则自由项1P R 一定为零。
6、超 静 定 结 构 中 杆 端 弯 矩 只 取 决 于 杆 端 位 移 。
7、位 移 法 可 解 超 静 定 结 构 ,也 可 解 静 定 结 构 。
8、图示梁之 EI =常数,当两端发生图示角位移时引起梁中点C 之竖直位移为(/)38l θ(向下)。
/2/22l l θθC9、图示梁之EI =常数,固定端A 发生顺时针方向之角位移θ,由此引起铰支端B 之转角(以顺时针方向为正)是-θ/2 。
θABl10、用位移法可求得图示梁B 端的竖向位移为ql EI 324/。
q l11、图 示 超 静 定 结 构 , ϕD 为 D 点 转 角 (顺 时 针 为 正), 杆 长 均 为 l , i 为 常 数 。
此 结 构 可 写 出 位 移 法 方 程111202i ql D ϕ+=/。
二、选择题1、位 移 法 中 ,将 铰 接 端 的 角 位 移 、滑 动 支 承 端 的 线 位 移 作 为 基 本 未 知 量 :A. 绝 对 不 可 ;B. 必 须 ;C. 可 以 ,但 不 必 ;D. 一 定 条 件 下 可 以 。
2、AB 杆 变 形 如 图 中 虚 线 所 示 , 则 A 端 的 杆 端 弯 矩 为 :A.M i i i l AB A B AB =--426ϕϕ∆/ ;B.M i i i l AB A B AB =++426ϕϕ∆/ ;C.M i i i l AB A B AB =-+-426ϕϕ∆/ ;D.M i i i l AB A B AB =--+426ϕϕ∆/。

飞行器结构力学基础李亚智航空学院·航空结构工程系第5章位移法5.1 概述第4章中讨论的力法是一种基于余能原理的、以“力”或“应力”作为基本未知量的、用来求解静不定结构内力和变形的方法。
位移法就是以位移作为基本未知量的分析结构内力和变形的方法,其理论基础是“虚位移原理”或“最小位能原理”。
位移法求解的思路是,根据变形条件、物理条件和平衡关系,建立以位移为基本变量的力的平衡方程,解方程得出未知位移,进而求出全部的位移和内力。
本章讨论的位移法,是以矩阵运算作为数学工具来处理结构位移计算的方法,故可称为矩阵位移法。
它是随着电子计算机的出现而得到发展的。
矩阵位移法早期较多地用于桁架、刚架等杆、梁式结构,直接采用刚度系数的物理意义来建立刚度方程,故又称为直接刚度法。
Turner和Clough等于1956年将刚架分析的位移法首次应用于连续介质问题;Clough首次提出有限元素(单元)法这一名称(The finite element method in plane stress analysis,平面应力分析的有限元素法,1960年)有限元素法广泛应用于多个工程领域。
直接刚度法和有限元素法有密切联系,是有限元素法的早期叫法。
矩阵位移法分析包含两个部分:(1)元素分析将结构分解成为有限个较小的单元(元素),称为离散化。
分析元素内力和位移之间的关系,建立元素刚度矩阵和刚度方程(平衡方程);(2)整体分析将各元素集合成整体结构,元素刚度方程集合成结构的刚度方程(总刚度方程),相应地元素刚度矩阵集合成结构的刚度矩阵(总刚度矩阵),在满足原结构变形协调和边界条件的前提下求解原结构的位移和内力。
5.2.1 杆元素⎥⎦⎤⎢⎣⎡=j i eu u δijijl iF jF x⎥⎦⎤⎢⎣⎡=j i eF F F 结点位移向量(列阵)ij ij l i u j u x 5.2 元素刚度矩阵及平衡方程从最简单的杆元素开始,讨论位移法的原理和分析过程。
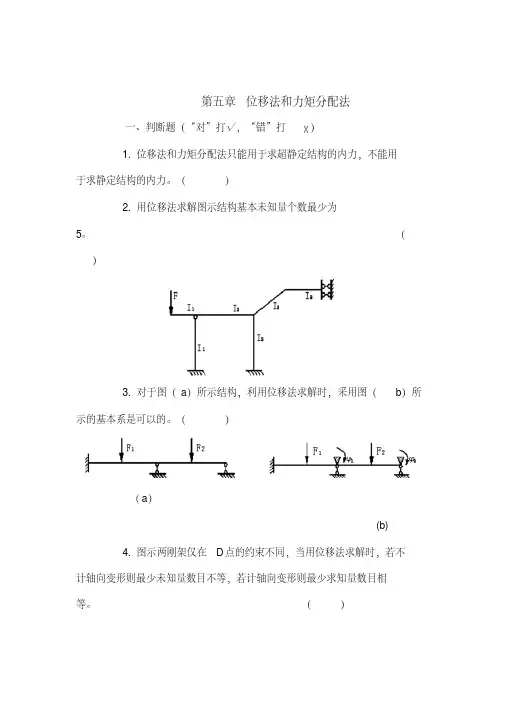
第五章位移法和力矩分配法一、判断题(“对”打√,“错”打)1.位移法和力矩分配法只能用于求超静定结构的内力,不能用于求静定结构的内力。
()2.用位移法求解图示结构基本未知量个数最少为5。
()3.对于图(a)所示结构,利用位移法求解时,采用图(b)所示的基本系是可以的。
()(a)(b)4.图示两刚架仅在D点的约束不同,当用位移法求解时,若不计轴向变形则最少未知量数目不等,若计轴向变形则最少求知量数目相等。
()(a)(b)5.图(a)所示结构的M图如图(b)所示。
()(a)(b)6.某刚架用位移法求解时其基本系如图所示,则其MF图中各杆弯矩为0,所以有附加连杆约束力FR1F=0。
( )7.图a结构用位移法计算的基本系如图b,则其2图如图c所示。
()(a) (b)(c)8.图示连续梁在荷载作用下各结点转角的数值大小排序为A>B>C> D. ( )9.图示两结构(EI均相同)中MA相等。
()(a)(b)10.下列两结构中MA相等。
()(a)(b)11.图示结构结点无水平位移且柱子无弯矩。
()12.图示结构下列结论都是正确的:. ( )13.用位移法计算图示结构,取结点B的转角为未知量,则. ( )14.图a对称结构(各杆刚度均为EI)可以简化为图b结构(各杆刚度均为EI)计算。
()(a)(b)15.图a对称结构可以简化为图b结构计算(各杆刚度不变)。
()(a)(b)16.图a对称结构可以简化为图b结构计算。
()(a) (b)17.图(a)所示对称结构,利用对称性简化可得计算简图,如图(b)所示。
()(a) (b) 18.图示结构中有c点水平位移和BE杆B点弯矩()19.图示结构的弯矩图与是否有AB杆和BC杆无关。
()20.用力矩分配法计算图示结构,则分配系数μCD=,传递系数。
()21.根据力矩分配法,图示结构最后弯矩有关系:()22.图a所示连续梁当线刚度i2?i1时,可简化为图b结构按力矩分配法计算。