第七章 位移法龙驭球结构力学
- 格式:ppt
- 大小:1.67 MB
- 文档页数:62

第7章位移法一。
教学目的掌握位移法的基本概念;正确的判断位移法基本未知量的个数;熟悉等截面杆件的转角位移方程;熟练掌握用位移法计算荷载作用下的刚架的方法了解位移法基本体系与典型方程的物理概念和解法。
二。
主要章节§7—1 位移法的基本概念§7-2 杆件单元的形常数和载常数-位移法的前期工作§7—3 位移法解无侧移刚架§7-4 位移法解有侧移刚架§7-5 位移法的基本体系§7—6 对称结构的计算*§7—7支座位移和温度改变时的位移法分析(选学内容)§7-8小结§7—9思考与讨论三. 学习指导位移法解超静定结构的基础是确定结构的基本未知量以及各个杆件的转角位移方程,它不仅可以解超静定结构,同时还可以求解静定结构,另外,要注意杆端弯矩的正负号有新规定。
四。
参考资料《结构力学(Ⅰ)—基本教程第3版》P224~P257第六章我们学习了力法,力法和位移法是计算超静定结构的两个基本方法,力法发展较早,位移法稍晚一些。
力法把结构的多余力作为基本未知量,将超静定结构转变为将定结构,按照位移条件建立力法方程求解的;而我们今天开始学的这一章位移法则是以结构的某些位移作为未知量,先设法求出他们,在据以求出结构的内力和其他位移。
由位移法的基本原理可以衍生出其他几种在工程实际中应用十分普遍的计算方法,例如力矩分配法和迭代法等.因此学习本章内容,不仅为了掌握位移法的基本原理,还未以后学习其他的计算方法打下良好的基础。
此外,应用微机计算所用的直接刚度法也是由位移法而来的,所以本章的内容也是学习电算应用的一个基础。
本章讨论位移法的原理和应用位移法计算刚架,取刚架的结点位移做为基本未知量,由结点的平衡条件建立位移法方程.位移法方程有两种表现形式:①直接写平衡返程的形式(便于了解和计算)② 基本体系典型方程的形式(利于与力法及后面的计算机计算为基础的矩阵位移法相对比,加深理解)§7-1 位移法的基本概念1。


§7–3 无侧移刚架的计算如果刚架的各结点(不包括支座)只有角位移而没有线位移,这种刚架叫做无侧移刚架。
连续梁的计算也属于无侧移问题。
小结:位移法的基本作法是先拆散,后组装。
组装的原则有二:首先,在结点处各个杆件的变形要协调一致;其次,装配好的结点要满足平衡条件。
例7-1 作图示刚架弯矩图。
§7–4 有侧移刚架的计算刚架分为无侧移和有侧移两类。
有侧移刚架除有结点转角外,还有结点线位移。
计算有侧移刚架的基本思路与无侧移相同,具体做法上增加了一些新内容:(1)在基本未知量中,要包括结点线位移;(2)在杆件计算中,要考虑线位移的影响;(3)在建立基本方程时,要增加与结点线位移对应的方程。
1 基本未知量的选取结点角位移:刚结点、刚绞结点的刚结点部分。
结点线位移:位移法中忽略轴力对变形的影响。
如何确定独立线位移?观察法只有一个线位移,只有一个线位移,有两个线位移,全部未知量有两个全部未知量有一个全部未知量有三个铰结体系法原结构的独立结点线位移的数目=铰结体系的自由度数=为了使此铰结体系成为几何不变而需添加的链杆数。
小结:1、用位移法计算有侧移刚架时,基本未知量包括结点转角和独立结点线位移。
2、结点转角的数目等于刚结点的数目,独立结点线位移的数目等于铰结体系的自由度的数目。
3、在选取基本未知量时,由于既保证了刚结点处各杆杆端转角彼此相等,又保证了各杆杆端距离保持不变,满足变形连续条件。
小结:位移法的基本方程都是根据平衡方程得出的。
基本未知量中每一个转角有一个相应的结点力矩平衡方程,每一个独立结点线位移有一个相应的截面平衡方程。
平衡方程的个数与基本未知量的个数彼此相等,正好解出全部基本未知量。
例7-2 作图示刚架弯矩图。
忽略横梁的轴向变形。
例7-3 作图示刚架内力图。
2.由荷载求固端弯矩2.由荷载求固端弯矩2.由荷载求固端弯矩载常数:荷载作用下的固端弯矩和固端剪力。
三种基本杆件(1)两端固定的梁;(2)一端固定、另一端简支的梁; (3)一端固定、另一端滑动支承的梁。



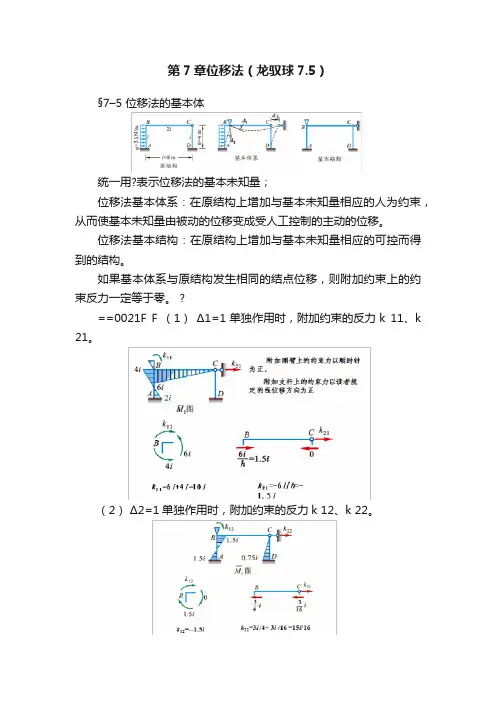
第7章位移法(龙驭球7.5)§7–5 位移法的基本体统一用?表示位移法的基本未知量;位移法基本体系:在原结构上增加与基本未知量相应的人为约束,从而使基本未知量由被动的位移变成受人工控制的主动的位移。
位移法基本结构:在原结构上增加与基本未知量相应的可控而得到的结构。
如果基本体系与原结构发生相同的结点位移,则附加约束上的约束反力一定等于零。
?==0021F F (1)Δ1=1单独作用时,附加约束的反力k 11、k 21。
(2)Δ2=1单独作用时,附加约束的反力k 12、k 22。
(3)荷载单独作用时,附加约束的反力F1P、F2P。
将三种情况下的附加约束反力叠加,得位移法典型方程的物理意义:基本结构在荷载和结点位移作用下,总附加约束反力等于零将求得的系数和自由项代入方程,求解得将三种情况下的弯矩图叠加对于n个基本未知量问题,位移法方程为k ii——主系数,恒大于零;k ij=k ji——副系数,可正、可负、可为零;作用在对称结构上的任意荷载,可以分为对称荷载和反对称荷载;在对称荷载作用下,变形是对称的,弯矩图和轴力图是对称的,而剪力图是反对称的;在反对称荷载作用下,变形是反对称的,弯矩图和轴力图是反对称的,而剪力图是对称的。
利用这些规则,计算对称结构时,可只取半边结构。
1 奇数跨对称结构(1)对称荷载在对称轴截面上,没有转角和水平位移,可有竖向位移。
(2)反对称荷载在对称轴截面上,没有竖向位移,可有转角和水平位移。
2 偶数跨对称结构(1) 对称荷载在对称轴截面上,没有转角和水平位移,由于不计轴向变形,也没有竖向位移。
(2)反对称荷载柱CD只有弯曲变形,可按抗弯刚度分成两个柱子。
C处的支杆对弯矩不起作用。
例7-4 作图示结构內力图。
吊杆的EA等于横梁EI的1/20m2。

第7章位移法7.1 复习笔记本章重点介绍了位移法的原理以及如何运用位移对超静定结构在各种荷载作用下的内力和位移进行求解。
位移法和力法像一幅对联,是超静定结构分析中的两个基本方法。
力法通过撤除多余约束达到简化计算的目的,而位移法通过添加约束达到此目的。
此外,二者对偶关系总结如下:力法:虚设单位力——求结构柔度——利用变形协调——求解未知约束力——算出结构内力。
位移法:虚设单位位移——求结构刚度——利用受力平衡——求解未知位移——算出结构内力。
两种方法殊途同归,在结构计算中应该综合考虑结构特点和求解目标选取合理的手法,使结构计算更加方便、快捷、准确。
一、位移法的基本概念(见表7-1-1)表7-1-1 位移法的基本概念二、杆件单元的形常数和载常数——位移法的前期工作采用位移法对刚架的等截面杆件进行分析时,杆件端部弯矩受两方面影响:①杆端位移产生的杆端弯矩——形常数;②外荷载产生的固端弯矩——载常数。
1.由杆端位移求杆端内力——形常数(见表7-1-2)表7-1-2 由杆端位移求杆端内力——形常数图7-1-12.由荷载求固端内力——载常数荷载作用下的杆端弯矩和杆端剪力,称为固端弯矩和固端剪力。
由于它们是只与荷载形式有关的常数,所以又称载常数,不同支座形式下杆件的固端弯矩和剪力值见表7-1-3。
表7-1-3 等截面杆件的固端弯矩和剪力三、位移法解无侧移刚架(见表7-1-4)表7-1-4 位移法解无侧移刚架四、位移法解有侧移刚架(表7-1-5)表7-1-5 位移法解有侧移刚架图7-1-2五、位移法的基本体系(见表7-1-6)表7-1-6 位移法的基本体系图7-1-3图7-1-4图7-1-5图7-1-6六、位移法解对称结构(见表7-1-7)表7-1-7 位移法解对称结构。

结构力学第7章课后答案(第四版龙驭球)练习题解答第1题题目:一个细长的圆柱形杆AB,长度为L=2L,直径为L=0.01L。
材料的弹性模量为L=200LLL。
杆的一端A固定,另一端B受集中力L=1000L作用在上面。
计算该杆在受力处的应变和应力。
解答:根据杨氏定律,杆的应力$\\sigma$和应变$\\varepsilon$之间的关系为:$$\\sigma = \\varepsilon \\cdot E$$应力可以通过受力和截面面积计算,公式为:$$\\sigma = \\frac{P}{A}$$应变可以通过杆的伸长量计算,公式为:$$\\varepsilon = \\frac{\\Delta L}{L}$$杆的伸长量$\\Delta L$可以通过杆的应变和长度计算,公式为:$$\\Delta L = \\varepsilon \\cdot L$$因为杆是圆柱形状,所以截面积L和直径L之间的关系为:$$A = \\frac{\\pi \\cdot d^2}{4}$$代入上述公式,可以得到应变和应力的计算公式:$$\\varepsilon = \\frac{\\Delta L}{L} = \\frac{P \\cdot L}{A \\cdot E}$$$$\\sigma = \\varepsilon \\cdot E = \\frac{P \\cdotL}{A}$$带入已知数据进行计算,可得:$$A = \\frac{\\pi \\cdot (0.01)^2}{4} \\approx 7.85\\times 10^{-5}m^2$$$$\\varepsilon = \\frac{1000 \\cdot 2}{7.85 \\times 10^{-5} \\cdot 200 \\times 10^9} \\approx 0.039$$$$\\sigma = \\varepsilon \\cdot E = 0.039 \\cdot 200\\times 10^9 \\approx 7.8 \\times 10^9 Pa$$所以该杆在受力处的应变约为0.039,应力约为7.8GPa。
