连环替代法举例
- 格式:doc
- 大小:29.00 KB
- 文档页数:3

连环替代法例题
连环替代法是一种逻辑推理方法,通过反复替换一个命题,从而得出结论的方法。
下面是一个连环替代法的例题,帮助你更好地理解这个推理方法。
假设有一个命题:如果今天下雨,那么马路上就会湿。
首先,我们需要找到这个命题的逆否命题。
逆否命题是将原命题的否定和逆序交换得到的命题。
在这个例子中,原命题是“如果今天下雨,那么马路上就会湿”,它的否定是“如果今天不下雨,那么马路上不会湿”,逆序交换后就是“如果马路上不湿,那么今天不下雨”。
接下来,我们使用连环替代法。
首先,我们假设马路上不湿,根据逆否命题,可以得出结论今天不下雨。
然后,我们再假设今天不下雨,根据原命题,可以得出结论马路上不湿。
通过连环替代法,我们得出了两个结论:如果马路上不湿,那么今天不下雨;如果今天不下雨,那么马路上不湿。
这意味着无论是马路上是否湿润,还是今天是否下雨,两者之间的关系是相互推导的,是等价的。
连环替代法在逻辑推理中非常常用,它可以帮助我们通过替代命题的方式,得出结论的等价命题。
通过这种方法,我们可以更好地理解和分析命题之间的关系,从而进行有效的推理和论证。
在实际应用中,连环替代法可以用于分析复杂的命题和问题,帮助我们更好地理解和解决问题。
掌握这种推理方法可以提升我们的逻辑思维能力,使我们更加熟练地进行推理和论证。

连环替代法的应用设F=a×b×c基数(过去、计划、标准)F0= a0×b0×c0实际数: F1= a1×b1×c1实际与基数的差异:F1 - F0连环替代法应用的基本步骤:(1)确定对比的基数(过去、计划、标准):F0= A0×B0×C0(2)替代A因素: A1×B0×C0(2)-(1):A因素变动对F的影响(3)替代B因素: A1×B1×C0(3)-(2):B因素变动对F的影响(4)替代C因素: A1×B1×C1(4)-(3):C因素变动对F的影响三因素的共同影响:F1 - F0简化分析法:(差额分析法)A因素的影响:(A1-A0)×B0×C0B因素的影响:A1×(B1-B0)×C0C因素的影响:A1×B1×(C1-C0)例题1:1.资料:F公司经营多种产品,最近两年的财务报表数据摘要如下(单位:万元)要求:进行以下计算、分析和判断(提示:为了简化计算和分析,计算各种财务比率时需要的存量指标如资产、所有者权益等,均使用期末数;一年按360天计算):(l)净利润变动分析:该公司本年净利润比上年增加了多少?按顺序计算确定所有者权益变动和权益净利率变动对净利润的影响数额(金额)。
答案:净利润变动分析:净利润增加=1200-1000=200万元因为:净利润=所有者权益×权益净利率设:F0=a0×b0所有者权益增加影响利润数额=(a1—a0)×b0=(15000-10000)×10%=500万元权益净利率下降影响利润数额=a1×(b1—b0)=15000×(8%-10%)=-300万元(2)权益净利率变动分析:确定权益净利率变动的差额,按顺序计算确定资产净利率和权益乘数变动对权益净利率的影响数额(百分点)。

中级连环替代法连环替代法是一种常用的解决问题的方法,它通过逐步替代问题中的变量来推导出最终的解答。
在中级连环替代法中,我们将探讨一些与数学和科学相关的问题,并使用连环替代法来解决它们。
一、数学问题1. 求解方程:假设我们需要求解一个二次方程,如x^2 + 3x + 2 = 0。
我们可以使用连环替代法来解决这个方程。
首先,我们可以将方程写成x = -3 - 2/x的形式,然后通过不断替代x的值来逼近方程的解。
2. 计算级数:假设我们需要计算一个级数的和,如1 + 1/2 + 1/4 + 1/8 + ...。
我们可以使用连环替代法来逐步计算级数的部分和,然后通过逼近无穷级数的和。
二、物理问题1. 弹簧振动:假设我们需要求解一个弹簧振动的问题,如一个质点在弹簧上的振动。
我们可以使用连环替代法来逐步计算质点的位置和速度,然后通过逼近实际的振动情况。
2. 热传导:假设我们需要求解一个热传导的问题,如一个物体在不同温度环境中的热传导过程。
我们可以使用连环替代法来逐步计算物体的温度分布,然后通过逼近实际的热传导情况。
三、化学问题1. 反应速率:假设我们需要求解一个化学反应速率的问题,如一个反应的速率与反应物浓度之间的关系。
我们可以使用连环替代法来逐步计算反应速率和反应物浓度,然后通过逼近实际的反应速率情况。
2. 化学平衡:假设我们需要求解一个化学平衡的问题,如一个反应的平衡常数与反应物浓度之间的关系。
我们可以使用连环替代法来逐步计算平衡常数和反应物浓度,然后通过逼近实际的化学平衡情况。
中级连环替代法是一种强大的解决问题的方法,它可以帮助我们逐步推导出复杂问题的解答。
通过灵活运用连环替代法,我们可以更好地理解和解决各种数学和科学问题。
希望本文对您有所帮助!。

连环替代法的公式连环替代法是一种在经济活动分析中常用的方法,它可以帮助我们深入了解各个因素对总体指标的影响程度。
那咱们就先来瞧瞧连环替代法的公式到底是啥样的。
连环替代法的公式其实并不复杂,咱先来说说基本的形式。
比如说有一个指标,它受到几个因素的影响,设这些因素分别为 A、B、C 等等,那么原本的指标值可以表示为 A0×B0×C0,经过变化后的指标值就是 A1×B1×C1 。
在计算某个因素的影响时,就保持其他因素不变,单独替换这个因素。
就拿一个简单的例子来说吧,假设一家小商店卖某种商品,原来每天的销售额 = 销售单价×销售数量×销售天数。
原本销售单价是 10 元,每天销售 50 件,销售 7 天,那销售额就是 10×50×7 = 3500 元。
后来单价涨到 12 元,销售数量变成 60 件,销售天数还是 7 天,新的销售额就是 12×60×7 = 5040 元。
咱们来算算单价变动的影响,先把单价以外的因素保持不变,也就是 50×7 = 350 ,然后用新单价 12 元减去原来的单价 10 元,得到 2 元。
2×350 = 700 元,这 700 元就是单价变动带来的销售额增加。
再说销售数量变动的影响,同样先把销售数量以外的因素固定,也就是 12×7 = 84 ,新销售数量 60 减去原来的 50 ,得到 10 。
84×10 = 840 元,这 840 元就是销售数量变动带来的销售额增加。
您看,通过这样一步步的计算和替代,咱们就能清楚地知道每个因素对总体销售额的具体影响有多大啦。
我之前在给学生们讲这个连环替代法的时候,就碰到过一个特别有趣的事儿。
有个学生特别较真儿,非要自己找个例子来验证。
他选的是计算自己每个月零花钱的变化因素,包括父母给的固定金额、自己帮忙做家务赚的额外奖励,还有节省下来的部分。

案例:某一公司2001年销售情况:销售A产品10000件,销售单价为500元/件,销售成本为300元/件,实现毛利为2000000元;
2002年销售情况销售A产品15000件,销售单价为550元/件,销售成本为330元/件,实现毛利为3300000元;因素分析法(连环替代法)分析毛利差额。
因素分析:2001年与2002年毛利差额为:
3300000 — 2000000=1300000元
销售毛利额=销售数量×(销售单价-销售单位成本)
①2001年A产品的毛利为10000×(500-300)=2000000元
②由于销售量的变化对毛利的影响:
15000×(500-300)=3000000元
②-① 3000000—2000000=1000000元
③由于销售单价的变化对毛利的影响:
15000×(550-300)=3750000元
③-② 3750000-3000000=750000元
④由于销售成本变化对毛利的影响:
15000×(550-330)=3300000元
④-③ 3300000-3750000=-450000元
三项因素合计影响使2002年比2001年毛利增加:
1000000+750000-450000=1300000元。


因素分析法「问题」1.连环替代法怎样替代总是搞不明白?「解答」连环替代法的原理是这样的:假设有一关联等式N0=A0×B0×C0 (1)在进行替代时,按照从左到右的顺序依次替代一个字母第一次替代:N1=A1×B0×C0 (2)第二次替代:第二次替代是在第一次替代的结果,即N1的基础上进行的,将B0替代成B1,即:N2=A1×B1×C0 (3)第三次替代:第三次替代是在第二次替代的结果,即N2的基础上进行的,将C0替代成C1,即:N3=A1×B1×C1 (4)A的影响是(2)-(1),即(A1-A0)×B0×C0B的影响是(3)-(2),即A1×(B1-B0)×C0C的影响是(4)-(3),即A1×B1×(C1-C0)「问题」2.差额分析法是连环替代法的一种简化形式,如何理解?「解答」连环替代法,是将各个因素依次替代,然后依次分析每个因素的变动对指标的影响。
而在差额分析法下,直接计算各因素的变动对指标的影响,即:A的影响是(A1-A0)×B0×C0B的影响是A1×(B1-B0)×C0C的影响是A1×B1×(C1-C0)贴现率:贴现利息与承兑汇票票面金额的比例就是银行承兑汇票贴现率。
那么未到期的银行承兑汇票贴现需要支付多少给银行作为利息呢?我们可以套用下面的贴现计算公式(设年贴现率为x%,月贴现率为y%)。
如果按照月利率计算,则贴现计算公式为:汇票面值-汇票面值×月贴现率y% ×贴现日至汇票到期日的月数;部分银行是按照天数来计算的,贴现计算公式为:汇票面值-汇票面值×年贴现率x% ×(贴现日-承兑汇票到期日)的天数/ 360。
以上公式只是大致的承兑汇票贴现计算公式,实际中,还要根据是否是外地汇票、实际银行托收时间等在计算中加、减天数。
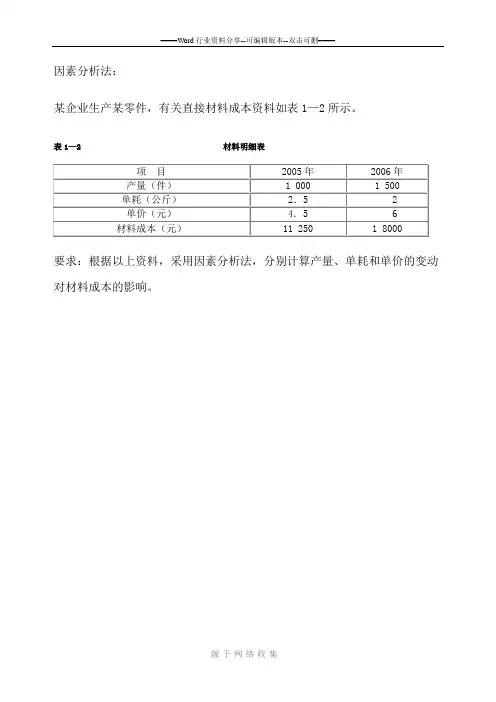
因素分析法:
某企业生产某零件,有关直接材料成本资料如表1—2所示。
表1—2 材料明细表
要求:根据以上资料,采用因素分析法,分别计算产量、单耗和单价的变动对材料成本的影响。
采用因素分析方法:
材料成本=产量×单耗×单价
基期材料成本=1 000×2.5×4.5=11 250(元)
本期材料成本=1 500×2×6=18 000(元)
材料成本差异=18 000-11 250=6 750(元)
产量变化对材料成本的影响=(1 500-1 000)×2.5×4.5=5 625(元)
单耗变化对材料成本的影响=1 500×(2-2.5)×4.5=-3 375(元)
单价变化对材料成本的影响=1 500×2×(6-4.5)=4 500(元)
由此可知,上述三种变化对材料成本的总影响是6 750(=5 625-3 375+4 500)元。
产量的提高使材料成本增加了5 625元,单价的上升也使得材料成本上升了4 500元,但是,单耗的减少却使得材料成本下降了3 375元,所以我们应该知道,在企业的生产管理中应该控制产量和产品价格的上升,并且保持单位耗用量的减少,这是以后企业发展的关键。

连环替代法的计算步骤[1]1.将基准值代入反映指标及影响因素关系的算式,基准值即为比较标准的数据,如计划值、上期值等;2.依次以一个因素的实际值替代基准值,计算出每次替代后指标数值,直到所有的因素都以实际值替代为止;3.把相邻两次计算的结果相比较,测算每一个替代因素的影响方向和程度;4.各因素的影响程度之和与指标的实际值与基准值的差额相等。
连环替代法的应用用代数式来描述连环替代法的应用过程:1、基期N=abc (abc之间也可以是加减乘除关系)实际期N'=a'b'c' 差额=N'-N2、我们假定替换的顺序是:先换a,再换b,最后换c3、替换a因素,得到N1=a'bc ,产生了新的经济指标N1,它是在基期水平上由于a因素的变动而出现的。
现在计算a因素单独变动带来的影响数:Na=N1-N4、替换b因素,得到N2=a'b'c ,产生了新的经济指标N2,它是在N1水平上由于b因素的变动而出现的。
现在计算b因素单独变动带来的影响数:Nb=N2-N15、替换C因素,得到N3=N'=a'b'c' ,产生了新的经济指标N3,它是在N2水平上由于C因素的变动而出现的。
现在计算C因素单独变动带来的影响数:Nc=N3-N2差额=N'-N=Na+Nb+Nc ,结束工作。
例:根据甲产品的下列资料,分析该产品90年销售利润的完成情况,计算各因素单独变动对指标的影响数。
解:销售利润的公式是:销售利润=销量*[单价*(1-税率)-单位成本]因素替换的顺序是先换销量,再换成本,再换单价,最后换税率。
这也是按照企业可控制性来排列的。
一般来说,企业要扩大利润,首先就是要扩大销量,其次才是降低成本和提高单价,而税率则是不可控的。
计划期销售利润=100*[2000*(1-10%)-1500]=30000=N实际期销售利润=80*[2200*(1-15%)-1450]=33600=N’差额=33600-30000=3600元1)先换销量:N1=80*[2000*(1-10%)-1500]=24000 ,注意销量为实际期数据,其他三者为基期数据。

连环替代法一.定义与条件连环替代法是根据因素之间的内在依存关系,依次测定各因素变动对经济指标差异影响的一种分析方法。
连环替代法的主要作用在于分析计算综合经济指标变动的原因及其各因素的影响程度。
应用连环替代法的前提条件:经济指标与它的构成因素之间有着因果关系,能够构成一种代数式。
注意这个代数式不一定是乘积关系,加减乘除都可以。
环替代法的指标顺序不一样,结果就会不同,所以,在应用连环替代法时,要正确规定各个因素的替换顺序,以保证分析计算结果的可比性。
如果要改变替换顺序,在计算每一个因素影响程度时,所依据的其他因素的条件不同,计算结果也会发生变化,分析的结论也会有所不同。
确定因素的替换顺序必须根据分析的目的,并根据各因素的依据关系和重要程度确定替换的先后顺序。
根据因素之间的相互依存关系,一般的替换顺序是:基本因素在前,从属因素在后;数量因素在前,质量因素在后;实物量指标在前,货币指标在后。
也就是在分析的因素中,如果既有基本的因素,又有从属的因素,一般先替换基本因素,然后再替换从属因素;如果既有数量指标又有质量指标,一般先替换数量指标,再替换质量指标;如果影响因素中既有实物量指标,又有价值量指标,一般先替换实物量指标,再替换价值量指标。
所以,指标顺序不是随便确定的,一般分析时会给出替代的顺序。
二.替代法的特点1、连环替代的顺序性。
2、替代因素的连环性。
连环替代法是严格按照各因素的排列顺序逐次以一个因素的实际数替换其基数。
除第一次替换外,每个因素的替换都是在前一个因素替换的基础上进行的。
3、计算结果的假设性。
运用这一方法在测定某一因素影响是,是以假定其他因素不变为条件的。
三.方法与应用用代数式来描述连环替代法的应用过程:1、基期N=abc (abc之间也可以是加减乘除关系)实际期N'=a'b'c' 差额=N'-N2、我们假定替换的顺序是:先换a,再换b,最后换c3、替换a因素,得到N1=a'bc ,产生了新的经济指标N1,它是在基期水平上由于a因素的变动而出现的。

第二次替代(单位材料消耗量因素)110×7×10=7700(元)(3)第三次替代(材料单价因素)110×7×12=9240(元)(4)
由于产品产量增加对材料费用的影响为
(2)-(1)=8800-8000=800(元)
由于单位产品材料消耗量节约对材料费用的影响为
(3)-(2)=7700-8800=-1100(元)
由于材料单价提高对材料费用的影响为
(4)-(3)=9240-7700=1540(元)
综合这3个因素对材料费用总额的影响为
800-1100+1540=1240(元)
4)最后换税率:N4=N'=33600 ,
N税率=33600-42400=-8800元
差额=N'-N=N销量+N成本+N单价+N税率
=-6000+4000+14400-8800=3600元
不管经济指标的表达式是一个什么样的代数式,只要给出了替代的顺序,就能够应用连环替代法去进行财务分析了。
注意,所有替换的因素的前面的因素都要保持实际水平,而排在它后面的因素都要保持基期水平。
一些高校编写的财务管理学教材、中级会计师职称的财务管理学教材和CPA财管教材,在介绍连环替代法时表达式都用的是N=abc这种乘积关系,致使有的人未能搞懂连环替代法的真正含义是什么,以为就只有乘积关系才能用连环替代法,因素之间是加减的关系,括号套括号的关系就不会用连环替代法了。
THANKS !!!
致力为企业和个人提供合同协议,策划案计划书,学习课件等等
打造全网一站式需求
欢迎您的下载,资料仅供参考。
不管经济指标的表达式是一个什么样的代数式,只要给出了替代的顺
序,就能够应用连环替代法去进行财务分析了。
注意,所有替换的因素的前面的因素都要保持实际水平,而排在它后面的因素都要保持基期水平。
一些高校编写的财务管理学教材、中级会计师职称的财务管理学教材和CPA 财管教材,在介绍连环替代法时表达式都用的是N=abc这种乘积关系,致使有的人未能搞懂连环替代法的真正含义是什么,以为就只有乘积关系才能用连环替代法,因素之间是加减的关系,括号套括号的关系就不会用连环替代法了。
连环替代法的步骤嘿,咱今儿个就来说说连环替代法!这连环替代法啊,就好比是你搭积木,一块一块往上垒,每一块都对最后的成果有着重要影响。
你看啊,咱要分析一个事儿,就像要搞清楚为啥你做的蛋糕没人家店里卖的好吃。
那咱就得一个因素一个因素地去看。
先看是不是面粉用得不对,这就好比是连环替代法里的第一个变量。
然后再看看是不是糖放少了,这就是第二个变量。
就这么一个一个查下去,总能找到问题所在。
比如说,你想知道为啥自己种的花儿没邻居家长得好。
那咱就从种子开始想,是不是种子质量不太好呀?这就是一个可能的因素。
然后再想想浇水,是不是浇多了或者浇少了?这又是一个方面。
接着看看施肥,有没有给足营养。
这就跟连环替代法一样,一个一个去替换,去验证。
这不就跟破案似的嘛!从一个一个线索里找真相。
而且这连环替代法可神奇了,它能让你清楚地看到每个因素的影响力有多大。
就像你知道了是浇水的问题让花儿长不好,那你以后就特别注意浇水这一块,可不就能把花儿养得美美的啦!再打个比方,你学习成绩不太好,那咱就用连环替代法来找原因呀。
是上课没认真听讲?还是课后作业没做好?或者是复习不够?一个一个排查,肯定能找到关键所在。
找到之后对症下药,成绩不就上去啦!你说这连环替代法是不是特别有用?它能帮你理清思路,找到问题的根源。
不像有些方法,糊里糊涂的,都不知道从哪儿下手。
这连环替代法就像是给你指了一条明路,让你顺着走就能找到答案。
咱平时生活里很多事儿都能用得上连环替代法呀。
比如说你想减肥,那你就得想想是吃得多了,还是运动少了,或者是作息不规律。
这不就是在分析影响你体重的因素嘛。
反正啊,学会了这连环替代法,就像多了一把解决问题的钥匙。
不管遇到啥难题,都能试着用它来分析分析。
你还别不信,自己试试就知道啦!这连环替代法真的是超厉害的,能让你把复杂的问题简单化,找到关键所在。
怎么样,是不是觉得很有意思呀?赶紧用起来吧!原创不易,请尊重原创,谢谢!。
2012年中级会计职称考试已经进⼊备考阶段,⼩编从中华会计校论坛整理了相关备考资料,供⼤家参考,祝⼤家学习愉快,梦想成真!
连环替代法和差额分析法
抛砖:
【问题】连环替代法怎样替代总是搞不明⽩?
引⽟:
【解答】连环替代法的原理是这样的:
假设有⼀关联等式N0=A0×B0×C0 (1)
在进⾏替代时,按照从左到右的顺序依次替代⼀个字母
第⼀次替代:N1=A1×B0×C0 (2)
第⼆次替代:第⼆次替代是在第⼀次替代的结果,即N1的基础上进⾏的,将B0替代成B1,即:N2=A1×B1×C0 (3)
第三次替代:第三次替代是在第⼆次替代的结果,即N2的基础上进⾏的,将C0替代成C1,即:N3=A1×B1×C1 (4)
A的影响是(2)-(1),即(A1-A0)×B0×C0
B的影响是(3)-(2),即A1×(B1-B0)×C0
C的影响是(4)-(3),即A1×B1×(C1-C0)
抛砖:
【问题】差额分析法是连环替代法的⼀种简化形式,如何理解?
引⽟:
【解答】连环替代法,是将各个因素依次替代,然后依次分析每个因素的变动对指标的影响。
⽽在差额分析法下,直接计算各因素的变动对指标的影响,即:
A的影响是(A1-A0)×B0×C0
B的影响是A1×(B1-B0)×C0
C的影响是A1×B1×(C1-C0)。
连环替代法的应用过程1、基期N=abc (abc之间也可以是加减乘除关系)实际期N'=a'b'c' 差额=N'-N2、我们假定替换的顺序是:先换a,再换b,最后换c3、替换a因素,得到N1=a'bc ,产生了新的经济指标N1,它是在基期水平上由于a因素的变动而出现的。
现今计算a因素单独变动带来的影响数:Na=N1-N4、替换b因素,得到N2=a'b'c ,产生了新的经济指标N2,它是在N1水平上由于b因素的变动而出现的。
现今计算b因素单独变动带来的影响数:Nb=N2-N15、替换C因素,得到N3=N'=a'b'c' ,产生了新的经济指标N3,它是在N2水平上由于C因素的变动而出现的。
现今计算C因素单独变动带来的影响数:Nc=N3-N2 差额=N'-N=Na+Nb+Nc。
结束工作。
例:根据甲产品的下列资料,分析该产品20*0年销售利润的完成情况,计算各因素单独变动对指标的影响数。
20*0年计划20*0年实际销量100台80台单价2000元2200元产品税率10% 15%单位成本1500 1450解:销售利润的公式是:销售利润=销量*[单价*(1-税率)-单位成本]因素替换的顺序是先换销量,再换成本,再换单价,最后换税率。
这也是按照企业可控制性来排列的。
一般来说,企业要扩大利润,首先就是要扩大销量,其次才是降低成本和提高单价,而税率则是不可控的。
计划期销售利润=100*[2000*(1-10%)-1500]=30000=N 实际期销售利润=80*[2200*(1-15%)-1450]=33600=N’ 差额=33600-30000=3600元1)先换销量N1=80*[2000*(1-10%)-1500]=24000 ,注意销量为实际期数据,其他三者为基期数据。
N销量=N1-N=24000-30000=-6000元2)再换成本注意销量和成本均为实际期数据,其他二者为基期数据。
连环替代法例题10题例题1:某企业生产产品,影响产品成本的因素有材料费用、人工费用和制造费用。
上年材料费用为100 万元,人工费用为80 万元,制造费用为60 万元,总成本为240 万元。
今年材料费用增加到120 万元,人工费用增加到90 万元,制造费用增加到70 万元,总成本变为280 万元。
1. 确定分析对象:-总成本变动额= 280 - 240 = 40 万元。
2. 确定各因素与总成本的关系:-上年总成本= 100 + 80 + 60 = 240 万元。
-今年总成本= 120 + 90 + 70 = 280 万元。
3. 进行连环替代:-以今年的材料费用、上年的人工费用和上年的制造费用计算替代后的总成本:120 + 80 + 60 = 260 万元。
-材料费用变动对总成本的影响= 260 - 240 = 20 万元。
-以今年的材料费用、今年的人工费用和上年的制造费用计算替代后的总成本:120 + 90 + 60 = 270 万元。
-人工费用变动对总成本的影响= 270 - 260 = 10 万元。
-以今年的材料费用、今年的人工费用和今年的制造费用计算替代后的总成本:120 + 90 + 70 = 280 万元。
-制造费用变动对总成本的影响= 280 - 270 = 10 万元。
4. 验证:-材料费用变动影响+ 人工费用变动影响+ 制造费用变动影响= 20 + 10 + 10 = 40 万元,与总成本变动额相等。
例题2:某公司销售产品,影响销售收入的因素有销售数量、销售单价和销售折扣。
上年销售数量为1000 件,销售单价为100 元/件,销售折扣为10%,销售收入为90000 元。
今年销售数量增加到1200 件,销售单价提高到110 元/件,销售折扣降低到8%,销售收入变为125040 元。
1. 确定分析对象:-销售收入变动额= 125040 - 90000 = 35040 元。
2. 确定各因素与销售收入的关系:-上年销售收入= 1000×100×(1 - 10%) = 90000 元。
连环替代法的分析运用某企业2010年3月生产产品所耗某种材料费的实际数是6720元,而其计划数是5400元。
实际比计划增加1320元。
由于材料费用是由产品产量、单位产品材料耗用量和材料单价三个因素的乘积构成的。
因此,可以把材料费用这一总指标分解为三个因素,现假设这三个因素的数值如下表所示。
一.连环替代法之不拿出式(一)替换顺序:产品产量单位产品材料消耗量材料单价计划指标:130×10×4=5200(元)①第一次替代:140×10×4=5600(元)②第二次替代:140×9×4=5040(元)③第三次替代得到:140×9×5=6300(元)④②-①=5600-5200=400(元)产量增加的影响③-②=5040—5600=-560(元)材料节约的影响④-③=6300-5040=1260(元)价格提高的影响400-560+1260=1100(元)全部因素的影响(二)替换顺序:产品产量材料单价单位产品材料消耗量计划指标:130×10×4=5200(元)①第一次替代:140×10×4=5600(元)②第二次替代:140×10×5=7000(元)③第三次替代得到:140×9×5=6300(元)④②-①=5600-5200=400(元)产量增加的影响③-②=7000—5600=1400(元)价格提高的影响④-③=6300-7000=-700(元)材料节约的影响400+1400-700=1100(元)全部因素的影响(三)替换顺序:单位产品材料消耗量产品产量材料单价计划指标:130×10×4=5200(元)①第一次替代:130×9×4=4680(元)②第二次替代:140×9×4=5040(元)③第三次替代得到:140×9×5=6300(元)④②-①=4680-5200=-520(元)材料节约的影响③-②=5040—4680=360(元)产量增加的影响④-③=6300-5040=1260(元)价格提高的影响-520+360+1260=1100(元)全部因素的影响(四)替换顺序:单位产品材料消耗量材料单价产品产量计划指标:130×10×4=5200(元)①第一次替代:130×9×4=4680(元)②第二次替代:130×9×5=5850(元)③第三次替代得到:140×9×5=6300(元)④②-①=4680-5200=-520(元)材料节约的影响③-②=5850—4680=1170(元)产量增加的影响④-③=6300-5850=450(元)价格提高的影响-520+1170+450=1100(元)全部因素的影响(五)替换顺序:材料单价产品产量单位产品材料消耗量计划指标:130×10×4=5200(元)①第一次替代:130×10×5=6500(元)②第二次替代:140×10×5=7000(元)③第三次替代得到:140×9×5=6300(元)④②-①=6500-5200=1300(元)材料节约的影响③-②=7000—6500=500(元)产量增加的影响④-③=6300-7000=-700(元)价格提高的影响1300+500-700=1100(元)全部因素的影响(六)替换顺序:材料单价单位产品材料消耗量产品产量计划指标:130×10×4=5200(元)①第一次替代:130×10×5=6500(元)②第三次替代得到:140×9×5=6300(元)④②-①=6500-5200=1300(元)材料节约的影响③-②=5850—6500=-650(元)产量增加的影响④-③=6300-5850=450(元)价格提高的影响1300-650+450=1100(元)全部因素的影响通过连环替代法的不拿出式的六组替换,我们可以看出虽然不同的替换顺序最后得到的材料费用差异相同,都是1100的差异额,但是不同的替换顺序使得材料节约,产量增加,价格提高对材料费用差异的影响在数值上也不同,并且在不同的替换方式中,材料节约,产量增加,价格提高对材料费用差异的影响程度不同。
差额=N'-N=N销量+N成本+N单价+N税率=-6000+4000+14400-8800=3600元
不管经济指标的表达式是一个什么样的代数式,只要给出了替代的顺序,就能够应用连环替代法去进行财务分析了。
注意,所有替换的因素的前面的因素都要保持实际水平,而排在它后面的因素都要保持基期水平。
一些高校编写的财务管理学教材、中级会计师职称的财务管理学教材和CPA 财管教材,在介绍连环替代法时表达式都用的是N=abc这种乘积关系,致使有的人未能搞懂连环替代法的真正含义是什么,以为就只有乘积关系才能用连环替代法,因素之间是加减的关系,括号套括号的关系就不会用连环替代法了。
-----精心整理,希望对您有所帮助!。