用短除法求最大公因数和最小公倍数

第八讲最大公因数和最小公倍数(一) 知识导航互质数：如果两个数的最大公因数是1，那么这两个数叫做互质数。

求几个数的最大公因数和最小公倍数，通常用短除法和分解质因数的方法。

即先分解质因数，然后将其公有的质因数相乘，则为它们的最大公因数；将公有的质因数和各自独有的质因数连乘，其积为最小公倍数。

精典例题例1：用短除法计算：（1）(54,90),[54,90] (2)(45,75,90)【分析】求最大公因数可用列举法，分解质因数法，小数缩倍法，大减小法，短除法。

求最小公倍数可用列举法，分解质因数法，大数扩倍法，短除法。

(54,90)=2×3×3=18,[54,90]= 2×3×3×3×5=270(45,75,90)= 3×5=15例2:利用分解质因数法找出下列各组数的最大公约数和最小公倍数。

(1)144和250 （2）240、80和96【分析】分解质因数法，最大公因数=公有质因数乘积，最小公倍数=公有质因数×独有质因数。

（1）144=2×2×2×2×3×3250=2×5×5×5（144，250）=2 【144，250】=2×2×2×2×3×3×5×5×5=18000（2）240=2×2×2×2×3×580=2×2×2×2×596=2×2×2×2×2×3（240，80，96）=2×2×2×2=16【240，80，96】=2×2×2×2×3×5×2=480.例3:利用辗转相除法求下列各组数的最大公约数。

找最大公因数1、几个数相同的因数叫作这个数的公因数；其中最大的一个叫作它们的最大公因数。

2、列举法求两个数的公因数和最大公因数的方法：先分别找出两个数各自所有的因数，再从中找出两个数的公因数，其中最大的一个就是这两个数的最大公因数。

3、短除法求两个数的最大公因数：如用短除法求18和27的最大公因数，用18和27的最小质因数3去除这两个数，看这两个数的商是不是互质；若不是互质，再接着往下除，一直除到商是互质为止，然后把所有的除数相乘，所得的积就是18和27的最大公因数。

18和27的最大公因数是3×3=9。

一、约分1、把一个分数的分子、分母同时除以公因数，分数的值不变，这个过程叫作约分。

2、分子、分母只含有公因数1的分数，叫作最简分数。

3、约分的方法：（1）逐次约分法：用分子和分母的公因数（1除外）逐次去除分子和分母，直到得出一个最简分数；（2）一次约分法：用分子和分母的最大公因数去除分子和分母。

二、最小公倍数1、几个数公有的倍数，叫作这几个数的公倍数。

其中最小的一个，叫作它们的最小公倍数。

2、求两个数的最小公倍数的方法：（1）列举法：先分别写出两个数各自的倍数，再从中找出公倍数和最小公倍数；（2）试除法：先写出两个数中较大数的倍数，再用这些数按从小到大的顺序依次除以较小数，第一个能被较小数整除的数就是它们的最小公倍数。

短除法求最小公倍数：如用短除法求18和27的最小公倍数，用18和27的最小质因数3去除这两个数，看这两个数的商是不是互质；若不是互质，再接着往下除，一直除到商是互质为止，然后把所有的除数和商相乘，所得的积就是18和27的最小公倍数。

18和27的最小公倍数是3×3×2×3=54。

三、分数的大小1、比较分数大小的方法：画图比较法，通分比较法。

2、通分的含义：把分母不相同的分数化成和原来分数相等、并且分母相同的分数，这个过程叫做通分。

3、通分的方法：用原来几个分数分母的公倍数作公分母，为了计算简便，通常选用最小公倍数作公分母，再把每个分数都化成用这个最小公倍数作分母的分数。

用短除法求最大公因数和最小公倍数课件最大公因数（Greatest Common Divisor，简称GCD）和最小公倍数（Least Common Multiple，简称LCM）是数学中常用的概念。

我们可以使用短除法来求解它们。

首先，让我们来解释一下什么是最大公因数。

最大公因数是指两个或多个整数共有的最大的因数。

我们可以通过短除法来找到最大公因数。

以两个整数a和b为例，我们首先将a除以b，并取得余数r。

然后，将b除以r，并再次取得余数r1。

我们重复这个过程，直到余数为0为止。

此时，最大公因数就是最后一次计算的非零余数。

例如，假设我们要求解整数36和48的最大公因数。

我们首先将36除以48，得到余数12。

然后，将48除以12，得到余数0。

因此，36和48的最大公因数是12。

接下来，让我们来解释一下什么是最小公倍数。

最小公倍数是指两个或多个整数的公有倍数中最小的一个。

我们可以通过短除法来找到最小公倍数。

以两个整数a和b为例，我们首先求解它们的最大公因数GCD。

然后，将a乘以b，再除以最大公因数GCD，即可得到最小公倍数LCM。

例如，假设我们要求解整数36和48的最小公倍数。

首先，我们计算它们的最大公因数，发现它们的最大公因数是12。

然后，我们将36乘以48，得到1728，再除以12，得到144。

因此，36和48的最小公倍数是144。

总结起来，最大公因数是两个或多个整数共有的最大因数，可以通过短除法找到；最小公倍数是两个或多个整数的公有倍数中最小的一个，可以通过将两个整数乘积除以最大公因数来求解。

2.3 短除法、最大公因数和最小公倍数的求法（小考复习精编专项练习）六年级数学小升初复习系列：第二章数和数的运算（含知识点与答案）【知识要点】一、短除法把一个合数分解成质因数，通常采用短除法。

那什么是短除法呢？先用能整除这个合数的质数去除它，一直除到商是质数为止，再把除数和商写成连乘的形式，这种方法就是短除法。

例如：所以，36分解质因数是：36＝2×2×3×3二、求几个数的最大公因数求几个数的最大公因数的方法：先找出这几个数的公因数，然后用这些公因数逐个去除这几个数，一直除到各个数所得的商只有公因数1时停止；然后，把所有的除数连乘起来，求出积，这个所得的积就是这几个数的最大公因数。

例如：求18和24的最大公因数所以，18和24的最大公因数是：2×3＝6三、求几个数的最小公倍数求几个数的最小公倍数的方法：先用全部数的公因数去除这几个数；或者其中某几个数的公因数去除，一直除到各数互质为止；然后，把所有的除数和商连乘起来，求出积，这个所得的积就是这几个数的最小公倍数。

例如：求12、15和20的最小公倍数所以，12、15和20的最小公倍数是：2×2×3×5×1×1×1＝60四、互质关系的数公因数只有1的两个数，叫做互质数，简称“互质”；互质数的两个数最大公因数是1。

成为互质关系的两个数，有下列几种情况：（1）1和任何自然数互质。

例如：1和9互质，最大公因数是1。

（2）相邻的两个自然数互质。

例如：4和5互质，最大公因数是1。

（3）不同的两个质数互质。

例如：3和11互质，最大公因数是1。

（4）当合数不是质数的倍数时，这个合数和这个质数也互质。

例如：9和13互质；27和7互质，最大公因数是1（5）两个合数的公因数只有1时，这两个合数也互质。

例如：12和25互质，最大公因数是1。

【优选练习】一、单选题1、下列各组数中，一定是互质数的是（）。

短除法求最小公倍数的道理
用短除法求最小公倍数时，与求最大公因数最大一点的不同，就是只要有两个数能被同一个数整除，就要继续除下去，直至商两两互质为止。

所有非零自然数的最小公因数是1，一个数倍数的个数无限，所以不存在最大公倍数。

因此我们经常遇见的是求大公因和小公倍。

求最大公因数和最小公倍数的方法有很多，最为常见和使用是短除法。

短除法是求最大公因数的一种方法，也可用来求最小公倍数。

使用分解质因数法来分别分解两个数的因数，再进行运算。

之后又演变为短除法。

短除法运算方法是先用一个除数除以能被它除尽的一个质数，以此类推，除到商是质数为止。

两个或多个整数公有的倍数叫作它们的公倍数，其中除0以外最轻的一个公倍数就叫作这几个整数的最轻公倍数。

整数a，b的最轻公倍数记作a，b同样的a，b，c的最轻公倍数记作a，b，c多个整数的最轻公倍数也存有同样的记号。

最大公因数和最小公倍数计算练习最大公因数和最小公倍数练
一、使用短除法求出以下数的最大公因数：
12和30
24和36
39和78
72和84
42和105
36和48
二、使用短除法求出以下数的最小公倍数：
25和30
24和39
60和84
12和24
45和60
12和18
42和105
36和48
三、使用短除法求出以下数的最大公因数和最小公倍数：45和60
27和76
27和80
四、填空：
15和5的最大公因数是5，最小公倍数是15；
9和3的最大公因数是3，最小公倍数是9；
9和18的最大公因数是9，最小公倍数是18；
11和44的最大公因数是11，最小公倍数是44；
30和60的最大公因数是30，最小公倍数是60；
13和91的最大公因数是13，最小公倍数是91；
7和12的最大公因数是1，最小公倍数是84；
8和11的最大公因数是1，最小公倍数是88；
1和9的最大公因数是1，最小公倍数是9；
8和10的最大公因数是2，最小公倍数是40；
6和9的最大公因数是3，最小公倍数是18；
8和6的最大公因数是2，最小公倍数是24；
10和15的最大公因数是5，最小公倍数是30；
4和6的最大公因数是2，最小公倍数是12；
5和9的最大公因数是1，最小公倍数是45；
29和87的最大公因数是29，最小公倍数是87；
30和15的最大公因数是15，最小公倍数是30；13、26和52的最大公因数是13，最小公倍数是52；
2、3和7的最大公因数是1，最小公倍数是42；16、32和64的最大公因数是16，最小公倍数是64.。

五年级最大公因数和最小公倍数公因数问题1：用短除法求下列各组数的最大公因数。

①12和18 ②34和102 ③15和50 ④12、24和36想：用短除法求两个数的最大公因数，一般用这两个数除以它们的公因数，一直除到所得的两个商只有公因数1为止,再把所有的除数连乘起来，所得积就是这两个数的最大公因数。

两个数的最大公因数用（ ）表示。

1218269323①②34102217511713③④155053101224362612182369312（34、102）= 2×17＝34（15、50）= 5（15、24、36）= 2×2×3=123试一试：求下列各组数的最大公因数（用短除法）①20和30②28和84③54和90④30、45和60问题2：求24、60和132三个数，共有多少个公因数？其中最大的公因数是多少？想：这道题可用列举法来解答，但比较麻烦。

我们可以用短除法求出这三个数的最大公因数，然后根据几个自然数最大公因数的因数个数等于这几个自然数公因数的个数的规律，找到这三个数的公因数。

24601322123066261533325（24、60、132）= 2×2×3=12，因为24、60和132的最大公因数是12，而12=22×3，得（2+1）×（1+1）=6，所以，24、60和132共有6个公因数，最大公因数是12。

解：11试一试：先用短除法求出每一组数的最大公因数，再求出每组数中公因数的总个数。

解：同时除以公因数2同时除以公因数2同时除以公因数3除到三个商只有公因数1为止（12、18）= 2×3＝6①16和24 ②28和70 ③150和180 ④60、75和150问题3：有三根木棒，分别长12厘米，44厘米，56厘米，把它们都截成同样长的小棒（整厘米），不许有剩余，每根小棒最长能有多少厘米？想：把每根木棒截成同样长的小棒后不许有剩余，每根小棒的长度必须是各自木棒长度的因数；把三根小棒截成同样长的小棒，不许有剩余，每根小棒的长就是这三根小棒的公因数；每根小棒最长多少厘米，就是求这三根小棒的最大公因数。

第23讲最大公因数和最小公倍数【探究必备】几个数公有的因数叫做这几个数的公因数，其中最大的一个叫做这几个数的最大公因数。

求几个数的最大公因数通常用短除法，即用几个数公有质因数连续去除，一直除到商里没有共同的质因数为止。

几个数公有的倍数叫做它们的公倍数，其中最小的一个叫做这几个数的最小公倍数。

求最小公倍数，可以从小到大一次列举，也可以用短除法。

短除法的一般步骤：1. 找出两个数的最小公因数（除1夕外）,列短除式，用最小公因数去除这两个数，得到两个商。

2. 找出两个商的最小公因数，用最小公因数去除两个商，得到新一级的两个商。

3. 以此类推，直到二商为互质数为止。

4. 把所有的公因数和最后的商乘起来，所得的积就是这两个数的最小公倍数。

【王牌例题】例1、一根铁丝长42厘米，一根铜丝长56厘米，现在要把它们截成同样长的小段，并且没有剩余，每段最长多少厘米？一共可以截成几段？分析与解答：要把它们截成同样长的小段并且没有剩余，说明每段的长度既能整除42,又能整除56,也就是说是这两个数的公因数，要使每段最长，就是公因数中最大的一个，即这两个数的最大公因数，42和56的最大公因数是14,所以每段最长是14厘米，那么铁丝可截42十14=3 （段），铜丝可截56十14=4 （段），因此一共可以截成3+4=7 （段）。

例2、一个新建的教室长9.6米，宽7.8米，现在要用一种地板方砖铺地面，不用切割，刚好用整数块。

铺这个教室至少要用多少块地板方砖？分析与解答：先把9.6米和7.8米化成以分米做单位的数，即9.6米=96分米，7.8米=78分米。

要使铺的地板方砖最少，那么方砖的面积要最大，也就是说方砖的边长要最大，根据用一种地板方砖铺地面，不用切割，刚好用整数块，可知方砖的边长既能整除96,又能整除78,即是这两个数的公因数，要使边长最大，就是这两个数的最大公因数，因为96和78的最大公因数是6,所以这种方砖的边长是6 （分米），那么方砖的面积为6X6=36 （平方分米），因此铺这个教室至少要用96X 78- 36=208 （块）地板方砖。

人教版五年级下册数学《最大公因数和最小公倍数》知识点及重点题分析最大公因数一、基础知识（1)定义:几个数公有的因数中，其中最大的公因数叫做它们的最大公因数。

,（2）求最大公因数的方法①列举法：②短除法:把各个数公有的质因数从小到大依次作为除数，连续去除这几个数，一直除到各个商是互质数为止，（也可以用较大的合数质公因数去除)然后把左半圈所有除数相乘，所得的积就是这几个数的最大公因数。

3 2 4此时3与2,4都互质，这三个数的公因数只有1，停止短除。

（即用短除法求最大公因数时，要使所有的数最后所得的商没有公因数就可，如果其中几个商有公因数，也不再除）。

因此，36，24，48的最大公因数是2×2×3＝12。

（3）求两个数最大公因数的特殊情况:①当两个数成倍数关系时，较小数就是这两个数的最大公因数。

②互质的两个数最大公因数是1。

（如连续的非零自然数、不同的质数等）(4）最大公因数和公因数的关系：所有的公因数都是这两个数的因数，最大公因数是这些公因数中最大的。

二、求最大公因数在计算中的应用作用：最大公因数在计算中的最重要的作用是约分，即把分数的分子和分母约成最大公因数为1的最简分数。

化最简分数最简捷的方法:①短除法求出最大公因数②用划线法分别约去分子分母的最大公因数，分别写出分子、分母被最大公因数除的商。

③练习:（1）填空：A α，b 都是非0自然数，如果a ÷b=10 ,那么α,b 的最大公因数是( ），最小公倍数是( ）。

解题分析：由题可知，α是b 的倍数,此时两数的最大公因数是其中的较小数b ，最小公倍数是其中的较大数α。

B 甲＝2×3×5，乙＝2×3×7，甲和乙的最大公因数是（ ）。

（2)化最简分数6318、9824、7545、5036 (3）判断： A 6318比216的分数单位小，所以6318比216小.（ ) B 分子分母是不同的质数,分子、分母的最大公因数一定是1。

找最大公因数和最小公倍数的几种方法最大公因数和最小公倍数是数学中常见的概念，它们分别用于求两个或多个数之间的共同约数和共同倍数。

下面我将为你介绍最大公因数和最小公倍数的几种计算方法。

一、最大公因数的计算方法：1.1质因数分解法：最大公因数可以通过将给定的两个或多个数分解质因数，找出它们的共同质因数，然后将这些质因数相乘得到最大公因数。

例如，求30和45的最大公因数：30=2×3×545=3×3×5它们的共同质因数是3和5，相乘得到最大公因数为151.2辗转相除法：辗转相除法又称为欧几里德算法，通过反复用两个数的较小数去除较大数，将余数作为新的两个数进行除法运算，直到余数为0，此时较小的那个数就是最大公因数。

例如，求56和72的最大公因数：72÷56=1余1656÷16=3余816÷8=2余0因此，最大公因数为81.3短除法：短除法是一种直观简便的方法，它通过反复用一个数去除另一个数，将余数作为新的两个数进行除法运算，直到余数为0，此时最后一次相除的除数就是最大公因数。

例如，求64和96的最大公因数：96÷64=1余3264÷32=2余0因此，最大公因数为32二、最小公倍数的计算方法：2.1质因数分解法：最小公倍数可以通过将给定的两个或多个数分解质因数，找出它们的所有质因数，并将每个质因数的最大次数相乘得到最小公倍数。

例如，求6和10的最小公倍数：6=2×310=2×5它们的所有质因数是2、3和5，它们的最大次数分别是1、1和1，因此最小公倍数为2×3×5=30。

2.2公式法：最小公倍数可以通过两个数的乘积除以它们的最大公因数来计算。

例如，求12和15的最小公倍数：最大公因数为3，乘积为12×15=180最小公倍数=乘积÷最大公因数=180÷3=602.3短除法：短除法也可以用于计算最小公倍数。

示例三︰运用短除法求两个数的最大公因数和最小公倍数一、课题基本资料学习范畴：数与代数学习重点：运用短除法求两个数的最大公因数和最小公倍数。

学生不须认识其原理。

已有知识： 1.学生已在2000年版小学数学课程学习单位4N5「公倍数和公因数」中，学会透过列举两个数的倍数，求该两个数的公倍数及最小公倍数；以及透过列出两个数的因数求该两个数的公因数及最大公因数。

学生已认识最大公因数和最小公倍数简称分别为“H.C.F.”和“L.C.M.”。

2.另外，学生已在2000年版小学数学课程学习单位4N2「除法（二）」中认识整除性，除数为2、5和10。

3.学生在初中数学修订课程学习单位1「基础计算」的学习重点1.1中，认识4、6、8和9的整除性判别方法。

4.学生亦应已透过过渡期学与教材料，学习3的整除性判别方法。

5.学生在初中数学修订课程学习单位1「基础计算」的学习重点1.3中，认识正整数的质因数分解。

［备注：部分学生可能在小学阶段曾经学习运用短除法求两个数的最大公因数和最小公倍数。

］规划建议：教师可把此课题融入初中数学修订课程学习重点1.4「求最大公因数和最小公倍数」的教学当中，教师亦可在其他合适地方引入此课题。

二、建议教学内容1.教师可与学生重温小学阶段所学的列举法。

♦例1：运用列举法，求12和18的最大公因数。

首先由小至大，列举12和18的所有因数，并圈出12和18的所有公因数。

12的因数：○1○2○3 4 ○61218的因数：○1○2○3○69 18从圈出的公因数中，可见6是12和18的最大公因数。

♦例2：运用列举法，求12和18的最小公倍数。

首先由小至大，列举12和18的首几个倍数，并圈出12和18的公倍数。

12的倍数：12 24 ○3648 60 ○72……18的倍数：18 ○3654 ○72……从圈出的公倍数中，可见36是12和18的最小公倍数。

2.教师可与学生讨论上述列举法的优点和缺点，从而引入短除法。

五年级最大公因数和最小公倍数公因数问题1：用短除法求下列各组数的最大公因数。

①12和18 ②34和102 ③15和50 ④12、24和36想：用短除法求两个数的最大公因数，一般用这两个数除以它们的公因数，一直除到所得的两个商只有公因数1为止,再把所有的除数连乘起来，所得积就是这两个数的最大公因数。

两个数的最大公因数用（ ）表示。

试一试：求下列各组数的最大公因数（用短除法）①20和30 ②28和84 ③54和90 ④30、45和60问题2：求24、60和132三个数，共有多少个公因数？其中最大的公因数是多少？想：这道题可用列举法来解答，但比较麻烦。

我们可以用短除法求出这三个数的最大公因数，然后根据几个自然数最大公因数的因数个数等于这几个自然数公因数的个数的规律，找到这三个数的公因数。

2460132 2123066261533325（24、60、132）= 2×2×3=12，因为24、60和132的最大公因数是12，而12=22×3，得（2+1）×（1+1）=6，所以，24、60和132共有6个公因数，最大公因数是12。

解：1112 18 26 93 2 3①②341022 17 51 171 3③④155053101224362612182369312（34、102）= 2×17＝34（15、50）= 5（15、24、36）= 2×2×3=123解： 同时除以公因数2 同时除以公因数2 同时除以公因数3 除到三个商只有公 因数1为止（12、18）= 2×3＝6试一试：先用短除法求出每一组数的最大公因数，再求出每组数中公因数的总个数。

①16和24 ②28和70 ③150和180 ④60、75和150问题3：有三根木棒，分别长12厘米，44厘米，56厘米，把它们都截成同样长的小棒（整厘米），不许有剩余，每根小棒最长能有多少厘米？想：把每根木棒截成同样长的小棒后不许有剩余，每根小棒的长度必须是各自木棒长度的因数；把三根小棒截成同样长的小棒，不许有剩余，每根小棒的长就是这三根小棒的公因数；每根小棒最长多少厘米，就是求这三根小棒的最大公因数。

文远教育__奥数__学科教师辅导教案（第 8讲）教师姓名：__沈军__学生__王姿匀__时间_2012_年_4_月 3_ 日 _8-_10 时段课题最大公约数和最小公倍数（一）教学目标1、通过练习法巩固行程问题的综合应用；2、理解质因数、最大公约数和最小公倍数；3、比较排列法和短除法求公约数、公倍数；4、理解并熟练掌握短除法；5、了解辗转相除法；6、通过分析公约数、公倍数解决实际问题个性化重点、难点重点：1、理解质因数、最大公约数和最小公倍数；2、理解并熟练掌握短除法难点：通过分析公约数、公倍数解决实际问题考点及考试要求1、求公约数、公倍数；2、判断说法对错；3、同余、分组问题教学内容：一、奥数风采展示：1、一辆客车和一辆货车分别从A、B两地相对开出，6小时后相遇，又经过4小时客车到达B地时，货车离终点还有188千米。

AB两地相距多少千米？2、甲、乙、丙三人行走的速度分别是每分钟60米、80米、100米。

甲、乙二人从B地同时同向出发，丙从A地同时同向去追甲和乙。

丙追上甲后又经过10分钟才追上乙。

求A、B两地的路程。

3、老师和小英为班级剪五角星，教师每分钟剪10个，剪了几分钟后小英接着剪，小英每分钟剪6个，两人共用8分钟，共剪了60个。

小英剪了多少个五角星？4、在100到200之间找出两个整数，使它的乘积等于30030。

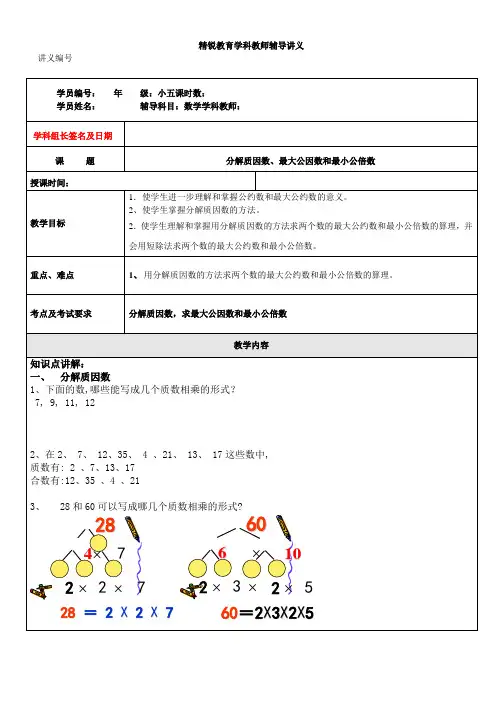
二、最大公约数一）分解质因数想一想：28和60可以写成哪几个质数相乘的形式?287×22×7×428 ＝ 2 X 2 X 760×23××660＝2X3X2X51025×每个合数都可以写成几个( )数相乘的形式,其中每个质数都是这个合数的( )数,叫做这个合数的质因数。

注意:质因数一定是一个质数。

练习：13 × 4=52,13和4都是52的因数吗？13和4都是52的质因数吗？什么是分解质因数呢?把一个合数用质因数相乘的形式表示出来，叫做分解质因数。