用短除法求最大公因数和最小公倍数概要

精锐教育学科教师辅导讲义讲义编号学员编号：年级：小五课时数：学员姓名：辅导科目：数学学科教师：学科组长签名及日期课题分解质因数、最大公因数和最小公倍数授课时间：教学目标1．使学生进一步理解和掌握公约数和最大公约数的意义。

2、使学生掌握分解质因数的方法。

2．使学生理解和掌握用分解质因数的方法求两个数的最大公约数和最小公倍数的算理，并会用短除法求两个数的最大公约数和最小公倍数。

重点、难点1、用分解质因数的方法求两个数的最大公约数和最小公倍数的算理。

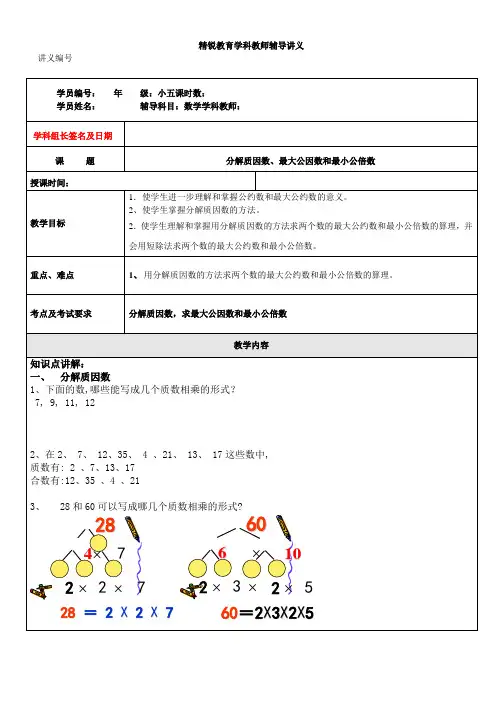
考点及考试要求分解质因数，求最大公因数和最小公倍数教学内容知识点讲解：一、分解质因数1、下面的数,哪些能写成几个质数相乘的形式？7, 9, 11, 122、在2、 7、 12、35、 4 、21、 13、 17这些数中,质数有: 2 、7、13、17合数有: 12、35 、4 、213、 28和60可以写成哪几个质数相乘的形式?287×22×7×428 ＝ 2 X 2 X 760×23××660＝2X3X2X51025×每个合数都可以写成几个( )数相乘的形式,其中每个质数都是这个合数的( )数,叫做这个合数的质因数。

4、13X4=52,13和4都是52的因数吗？13和4都是52的质因数吗？5、什么是分解质因数呢?把一个合数用质因数相乘的形式表示出来，叫做分解质因数。

（1）用短除法把下面各数分解质因数.55 605551155 = 5×11260233015560=2×2×3×5（2）能用短除法把下面各数分解质因数.80 12 16 72练习：一、选一选。

(1)把10分解质因数是( )A.10=2×5B.10=1×2×5C.10=1×10(2)把27分解质因数是( )A.3×9=27B.3×3×3=27C.27=3×3×3 （2）看谁是小判官①把35分解质因数是 35=1×5×7（）②把49分解质因数是7×7=49 ( )③把30分解质因数是30=2×3×5 ( )④51不能分解质因数. ( )二、用短除法找最大公因数1．用排列因数的方法求18和24的最大公因数。

用短除法求最小公倍数的方法步骤文/ 春秋书生教材介绍的是采用列举法和分解质因法求两个数的最小公倍数，这两种方法对于对较小数的求最小公倍数比较适用，但对较大的数来说，做起来就比较麻烦了，下面是我总结的用短除法求最小公倍数的方法步骤：第一步：找出两数的最小公因数，列短除式，用最小公因数去除这两个数，得到两个商；第二步：然后找出两个商的最小公因数，用最小公因数去除这两个商，得到新一级的两个商；第三步：以此类推，直到这两个商为互质数（即两个商只有公因数1）为止；第四步：将所有的公因数及最后的两个商相乘，所得积就是我们要求的两个数的最小公倍数。

例：甲数=2X 3X 7X A,乙数=2X 5X 7X A,请问当A=（）时，甲乙两数的最大公因（约）数是42。

A.2B.3C.5D.7题：求96,30,132 的最小公倍数1．30=2X3X5 2. 96=2 5X5 3. 132=2 2X3X11所以【96,30,132 】=25X3X5X11=5280题：求【150,42 】因为（150,42 ）=21 所以【150,42 ] =150X 42-21=210题：把一长60 厘米、宽40 厘米的长方形纸板剪成边长是整数厘米数的小正方形,且无剩余,最少可以剪成多少块？解：(60,40 ) =20……这是小正方形的边长。

(60- 20)X( 40- 20) =6 (块)或用面积计算：(60X 40)-( 20X 20) =6 (块)题：用长5厘米、宽3厘米的长方形纸片摆成一个正方形(中间无空隙)，至少要用多少个长方形纸片？解：(5,3 ) =15 (厘米)……这是正方形的边长。

(15-5)X( 15-3)=15(个)长方形如果一个数能被第二个数整除，那么这两个数的最大公因数是第二个数。

几个数公有的倍数，叫做它们的公倍数，其中最小的公倍数，叫做它们的最小公倍数。

说出下列各组数的最小公倍数。

(口答)第一组：12和4(12) 6 和18 (18) 10 和70(70)倍数关系：最小公倍数是大数。

用短除法求最小公倍数的方法步骤文/春秋书生教材介绍的是采用列举法和分解质因法求两个数的最小公倍数，这两种方法对于对较小数的求最小公倍数比较适用，但对较大的数来说，做起来就比较麻烦了，下面是我总结的用短除法求最小公倍数的方法步骤：第一步：找出两数的最小公因数，列短除式，用最小公因数去除这两个数，得到两个商；第二步：然后找出两个商的最小公因数，用最小公因数去除这两个商，得到新一级的两个商；第三步：以此类推，直到这两个商为互质数（即两个商只有公因数1）为止；第四步：将所有的公因数及最后的两个商相乘，所得积就是我们要求的两个数的最小公倍数。

例：甲数=2×3×7×A，乙数=2×5×7×A，请问当A=（）时，甲乙两数的最大公因（约）数是42。

A.2B.3C.5D.7题：求96,30,132的最小公倍数1．30=2×3×5 2. 96=25×5 3. 132=22×3×11所以【96,30,132】=25×3×5×11=5280题：求【150,42】因为（150,42）=21 所以【150,42】=150×42÷21=210题：把一张长60厘米、宽40厘米的长方形纸板剪成边长是整数厘米数的小正方形，且无剩余，最少可以剪成多少块？解：（60,40）=20……这是小正方形的边长。

（60÷20）×（40÷20）=6（块）或用面积计算：（60×40）÷（20×20）=6（块）题：用长5厘米、宽3厘米的长方形纸片摆成一个正方形（中间无空隙），至少要用多少个长方形纸片？解：（5,3）=15（厘米）……这是正方形的边长。

（15÷5）×（15÷3）=15（个）长方形如果一个数能被第二个数整除，那么这两个数的最大公因数是第二个数。

讲义编号学员编号：年级：小五 课时数：学员姓名：辅导科目：数学学科教师：学科组长签名及日期课 题分解质因数、最大公因数和最小公倍数 授课时间：教学目标 1．使学生进一步理解和掌握公约数和最大公约数的意义。

2、使学生掌握分解质因数的方法。

2．使学生理解和掌握用分解质因数的方法求两个数的最大公约数和最小公倍数的算理，并会用短除法求两个数的最大公约数和最小公倍数。

重点、难点 1、 用分解质因数的方法求两个数的最大公约数和最小公倍数的算理。

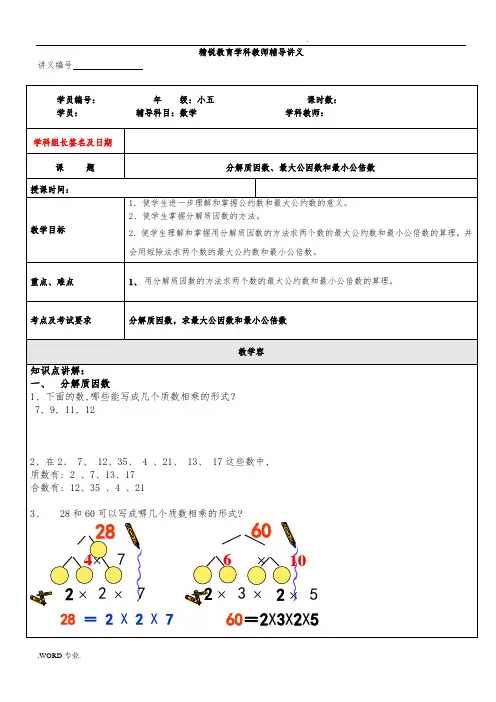
考点及考试要求 分解质因数，求最大公因数和最小公倍数教学内容知识点讲解：一、 分解质因数1、下面的数,哪些能写成几个质数相乘的形式？7, 9, 11, 122、在2、 7、 12、35、 4 、21、 13、 17这些数中,质数有: 2 、7、13、17合数有: 12、35 、4 、213、 28和60可以写成哪几个质数相乘的形式?287×22×7×428 ＝ 2 X 2 X 760×23××6 60＝2X 3X 2X 51025×每个合数都可以写成几个()数相乘的形式,其中每个质数都是这个合数的( )数,叫做这个合数的质因数。

4、13X4=52,13和4都是52的因数吗？13和4都是52的质因数吗？5、什么是分解质因数呢?把一个合数用质因数相乘的形式表示出来，叫做分解质因数。

（1）用短除法把下面各数分解质因数.55605551155 = 5×11260233015560=2×2×3×5（2）能用短除法把下面各数分解质因数.80 121672练习：一、选一选。

(1)把10分解质因数是()A.10=2×5B.10=1×2×5C.10=1×10(2)把27分解质因数是()A.3×9=27B.3×3×3=27C.27=3×3×3（2）看谁是小判官①把35分解质因数是 35=1×5×7（）②把49分解质因数是7×7=49 ( )③把30分解质因数是30=2×3×5( )④51不能分解质因数. ( )二、用短除法找最大公因数1．用排列因数的方法求18和24的最大公因数。

示例三︰运用短除法求两个数的最大公因数和最小公倍数一、课题基本资料学习范畴：数与代数学习重点：运用短除法求两个数的最大公因数和最小公倍数。

学生不须认识其原理。

已有知识： 1.学生已在2000年版小学数学课程学习单位4N5「公倍数和公因数」中，学会透过列举两个数的倍数，求该两个数的公倍数及最小公倍数；以及透过列出两个数的因数求该两个数的公因数及最大公因数。

学生已认识最大公因数和最小公倍数简称分别为“H.C.F.”和“L.C.M.”。

2.另外，学生已在2000年版小学数学课程学习单位4N2「除法（二）」中认识整除性，除数为2、5和10。

3.学生在初中数学修订课程学习单位1「基础计算」的学习重点1.1中，认识4、6、8和9的整除性判别方法。

4.学生亦应已透过过渡期学与教材料，学习3的整除性判别方法。

5.学生在初中数学修订课程学习单位1「基础计算」的学习重点1.3中，认识正整数的质因数分解。

［备注：部分学生可能在小学阶段曾经学习运用短除法求两个数的最大公因数和最小公倍数。

］规划建议：教师可把此课题融入初中数学修订课程学习重点1.4「求最大公因数和最小公倍数」的教学当中，教师亦可在其他合适地方引入此课题。

二、建议教学内容1.教师可与学生重温小学阶段所学的列举法。

♦例1：运用列举法，求12和18的最大公因数。

首先由小至大，列举12和18的所有因数，并圈出12和18的所有公因数。

12的因数：○1○2○3 4 ○61218的因数：○1○2○3○69 18从圈出的公因数中，可见6是12和18的最大公因数。

♦例2：运用列举法，求12和18的最小公倍数。

首先由小至大，列举12和18的首几个倍数，并圈出12和18的公倍数。

12的倍数：12 24 ○3648 60 ○72……18的倍数：18 ○3654 ○72……从圈出的公倍数中，可见36是12和18的最小公倍数。

2.教师可与学生讨论上述列举法的优点和缺点，从而引入短除法。

用短除法求最小公倍数的方法步骤文/春秋书生教材介绍的是采用列举法和分解质因法求两个数的最小公倍数，这两种方法对于对较小数的求最小公倍数比较适用，但对较大的数来说，做起来就比较麻烦了，下面是我总结的用短除法求最小公倍数的方法步骤：第一步：找出两数的最小公因数，列短除式，用最小公因数去除这两个数，得到两个商；第二步：然后找出两个商的最小公因数，用最小公因数去除这两个商，得到新一级的两个商；第三步：以此类推，直到这两个商为互质数（即两个商只有公因数1）为止；第四步：将所有的公因数及最后的两个商相乘，所得积就是我们要求的两个数的最小公倍数。

例：甲数=2×3×7×A，乙数=2×5×7×A，请问当A=（）时，甲乙两数的最大公因（约）数是42。

A.2B.3C.5D.7题：求96,30,132的最小公倍数1．30=2×3×5 2. 96=25×5 3. 132=22×3×11所以【96,30,132】=25×3×5×11=5280题：求【150,42】因为（150,42）=21 所以【150,42】=150×42÷21=210题：把一张长60厘米、宽40厘米的长方形纸板剪成边长是整数厘米数的小正方形，且无剩余，最少可以剪成多少块？解：（60,40）=20……这是小正方形的边长。

（60÷20）×（40÷20）=6（块）或用面积计算：（60×40）÷（20×20）=6（块）题：用长5厘米、宽3厘米的长方形纸片摆成一个正方形（中间无空隙），至少要用多少个长方形纸片？解：（5,3）=15（厘米）……这是正方形的边长。

（15÷5）×（15÷3）=15（个）长方形如果一个数能被第二个数整除，那么这两个数的最大公因数是第二个数。

求最大公因数和最小公倍数的简便方法说实话求最大公因数和最小公倍数这事，我一开始也是瞎摸索。

就说求最大公因数吧，我最开始就知道那老方法，列举法。

比如求12和18的最大公因数，就把12的因数1、2、3、4、6、12都列出来，再把18的因数1、2、3、6、9、18列出来，然后找它们共同的因数，其中最大的6就是最大公因数了。

但是吧，这方法很费时间，数字一大就特麻烦。

后来我就试过短除法。

还拿12和18举例哈。

把这两个数并排写，然后找一个能同时整除它们的最小质数，就像2，用2去除12得到6，18得到9，接着再找能同时整除6和9的数，这时候是3，6除以3得2，9除以3得3。

除到这两个数互质了为止。

然后把左边的除数相乘，2乘以3等于6，这6就是12和18的最大公因数。

这方法吧，一开始我老弄错这个除到什么时候停止，有时候没除到互质就停了，就得出错结果了。

那求最小公倍数呢，其实用短除法也行。

还是12和18，用短除法除完后，把左边的除数和最后的商全部乘起来。

就是2乘以3乘以2乘以3等于36，36就是12和18的最小公倍数。

还有一种求几个数的最大公因数的辗转相除法。

我试过拿两个比较大的数，像78和18来说。

用78除以18得到商4余6，然后就用除数18除以余数6得到商3余0，当余数为0的时候，这时候的除数6就是78和18的最大公因数了。

不过这个方法有时候容易把被除数和除数弄混，刚开始用挺容易错的。

我还发现求最小公倍数有种特殊情况呢。

要是两个数是互质数，像3和5吧，那它们的最小公倍数就是这两数相乘，就是3乘以5等于15，最大公因数就是1。

还有，如果一个数是另一个数的倍数，比如6和12，那最大公因数就是小的那个数6，最小公倍数就是大的那个数12。

这都是我一直摸索出来的小经验，这些方法掌握好了，求最大公因数和最小公倍数就没那么难了。

哦对了，多做点练习题也是关键，这样能把这些方法用得更熟练。

比如24和36呀，8和15呀，多做做这类题，慢慢就找到感觉了。