下载文档原格式
第27讲 求一个数的几分之几的应用题【探究必备】1. 求一个数的几分之几是多少用乘法计算。
一个数×几分之几=几分之几对应的数量。
2. 解题关键：找准单位“1” ，写出数量关系式，列式解答。
【王牌例题】例1、实验小学六年级共有学生675人，其中男生占53。
男生有多少人？分析与解答：用分数乘法解决问题时，首先要找准单位“1” ，再根据题意进行解答。
男生占53，就是把实验小学六年级的总人数看做单位“1” ，单位“1”是已知数，求男生有多少人，就是求一个数的几分之几是多少用乘法计算，即一个数×几分之几，因此男生有675×53=405（人）。
例2、实验小学六年级有男生405人，女生的人数是男生人数的32。
女生有多少人？分析与解答：例2和例1一样，都是求一个数的几分之几是多少的实际问题。
不同的是例1中分析的是部分与整体的关系，例2中分析的是部分与部分的关系，但运用的数量关系是一样的，解题思路也是一致的。
女生的人数是男生人数的32，就是把男生人数看作单位“1” ，单位“1”是已知数，求女生有多少人，就是求一个数的几分之几是多少用乘法计算，即405的32是多少，因此女生有405×32=270（人）。
例3、一台笔记本电脑，原价是4200元，现在的价格比原来的价格降低了71。
现价比原价降低了多少元？分析与解答：现在的价格比原来的价格降低了71，就是把原来的价格看作单位“1” ，原价×71=现价比原价降低了多少元。
所以求现价比原价降低了多少元，就是求4200的71是多少，即现价比原价降低了4200×71=600（元）。
例4、 王老师要录一篇2700字的文章，已经录了52。
还剩多少字没有录？分析与解答：要求还剩多少字没有录，应先求已经录了多少字，根据已经录了52，这里是把这篇文章的总字数看作单位“1” ，文章的总字数×52=已经录的字数，即已经录了2700×52=1080（字），所以还剩2700-1080=1620（字）没有录。
一个数乘以分数的数学教案一个数乘以分数的数学教案「篇一」一个数乘以分数的教案范文第二课时：一个数乘以分数教学内容：教科书第４～６页，练习二第１～４题。
教学目的：１、使学生理解一个数乘以分数的意义，学会分数乘以分数的计算方法。
２、通过操作、观察培养学生的推理能力，发展学生的思维。
教具准备：第４页例２的插图。
长方形纸。
教学过程（）：一、复习。
１．计算下列各题并说出计算方法。
２．上面各题都是分数乘以整数，说一说分数乘以整数的意义。
二、新课。
引入：这节课我们来学习一人数乘以分数的意义和计算方法。
（板书课题：一个数乘以分数）１．理解一个数乘以分数的意义。
（１）第一幅图：一瓶桔汁重千克，３瓶重多少千克？怎样列式？指名列式，板书：问：表示什么意思？指名回答，板书：求３个或求的３倍。
（２）出示第二幅图：一瓶桔汁重千克，半瓶重多少千克？怎样列式？怎样表示半瓶？指名回答：半瓶用表示；式子为：。
说明：是求的一半是多少，也就是求的是多少。
板书：求的。
（３）出示第三幅图：一瓶桔汁重千克，瓶重多少千克？怎样列式？指名回答，板书：，问：表示什么意思？指名回答，板书：求的。
２．引导学生小结。
①．指出三个算式都是分数乘法，比较三个算式的不同点：第一个算式与第二、三个算式中乘数有什么不同？想一想：第一个算式与第二、三个算式中乘法的意义有没有不同。
有什么不同？引导学生得出：分数乘以整数的意义和整数乘法的意义相同；而一个数乘以分数的意义是求这个数的几分之几是多少。
学生齐读课本的结语。
练习：．课本的做一做１、２题。
．说一说下列算式的意义。
３．理解分数乘以分数的计算方法。
（１）出示例３（先出示第一个问题）。
问：你根据什么列出式子？得出：根据“工作效率×工作时间＝工作总量”列出式子：。
问：如果我们用一个长方形表示１公顷，那么公顷怎样表示？学生回答后，教师出示例３的图（１）问：公顷的` 是什么意思？出示例３图（２）要求学生观察图（２），问：在图中的对于１公顷来说，是１公顷的几分之几？引导得出：观察这个式子有什么特点？出示例３的第二个问题。
人教版数学五升六暑期精编专项讲义—新课衔接站第一单元《分数乘法》第2课《一个数乘分数》学习目标：1.使学生理解一个数乘分数的意义.掌握分数乘以分数的计算法则。
2.学会分数乘分数的简便计算。
3.通过一个数乘以分数应用的广泛性事例.对学生进行学习目的性教育.激发学生学习动机和兴趣。
新知讲解：【典例引入】（2020六上·侯马期末）先计算.并在图中涂色表示×。
× =【答案】×= .。
【解析】【分析】分数乘分数.用分子相乘的积作分子.分母相乘的积作分母.据此计算再涂色表示.图中画斜线部分即为所求。
【变式训练】【变式1】看图列式计算【答案】解：75×＝125(朵)答：玫瑰花有125朵.【解析】【分析】观察线段图可知.把菊花的朵数看作单位“1”.已知菊花的朵数.求比菊花朵数多是多少朵.用菊花的朵数×(1+)=玫瑰的朵数.据此列式解答.【变式2】水果批发商购进10吨水果.上午卖出了 .下午卖出了吨.一共卖出了多少吨水果？【答案】10×+=2+=（吨）答：一共卖出了吨水果.【解析】【分析】根据题意可知.先求出上午卖出的水果吨数.用购进的水果总质量×上午卖出的占总量的分率=上午卖出的水果质量.然后用上午卖出的水果质量+下午卖出的水果质量=一共卖出的水果质量.据此列式解答.【知识点总结】分数乘法计算法则：1.分数乘整数的运算法则是：分子与整数相乘.分母不变。
（1）为了计算简便能约分的可先约分再计算。
（整数和分母约分）（2）约分是用整数和下面的分母约掉最大公因数。
（整数千万不能与分母相乘.计算结果必须是最简分数）。
2.分数乘分数的运算法则是：用分子相乘的积做分子.分母相乘的积做分母。
（分子乘分子.分母乘分母）（1）如果分数乘法算式中含有带分数.要先把带分数化成假分数再计算。
（2）分数化简的方法是：分子.分母同时除以它们的最大公因数。
（3）在乘的过程中约分.是把分子.分母中.两个可以约分的数先划去.再分别在它们的上.下方写出约分后的数。
一个数乘以分数简便计算教学内容：教材，例2、例3及做一做，练习1－4题。
素质教育目标（一）知识教学点1．使学生理解一个数乘以分数的意义，掌握分数乘以分数的计算法则。
2．学会分数乘以分数的简便计算。
（二）能力训练点1．使学生能够正确应用分数乘以分数的计算法则，较熟练地进行计算。
2．通过操作、观察，培养学生的推理能力，发展学生思维。
（三）德育渗透点通过一个数乘以分数应用的广泛性事例，对学生进行学习目的性教育，激发学生学习动机和兴趣。
教学重点理解一个数乘以分数的意义，掌握分数乘以分数的计算方法。
教学难点推导算理，总结法则。
教具、学具准备1．教科书例2的插图制成多媒体。
2．教师和学生每人准备一张长15厘米，宽10厘米的长方形纸。
5页例3的图制成抽拉片。
教学步骤一、铺垫孕伏1．计算下面各题，并说出计算方法。
2．说出上面各式所表示的意义。
3．引出课题我们复习了分数乘以整数的意义和计算方法，这节课我们学习一个数乘以分数的意义和计算方法。
（板书课题：一个数乘以分数）二、探究新知1．教学一个数乘以分数的意义。
（1）出示例2克，3瓶重多少千克？让学生独立解答，订正时教师问：你是怎么想的？启发学生③（幻灯出示第三幅图）放手让学生自己观察图，复述图意，根据图2推想出算式及算式表示的意思。
（自由结组互相交流）（2）观察比较：①比较三个算式异同点：学生发现：相同点：三个等式都是分数乘法。
不同点：第一个算式的乘数是整数，第二、三个算式的乘数都是分数。
②比较三个算式表示的意义：使学生弄清第一个算式与第二、三个算式表示的意义不同。
（3）引导、概括、总结是多少。
（板书：求一个数的几倍）从第二、三两算式表示的意义先引导学少。
（板书：求一个数的几分之几）让学生试着总结一个数乘以分数的意义，然后阅读课本中的结语。
（4）归纳整理：①引导学生归纳出求一个数的几倍，求一个数的几分之几都用乘法计算。
②教师说明：分数乘以整数的意义和整数乘法的意义相同，而一个数乘以分数的意义是求这个数的几分之几是多少。
一个数乘几分之几表示的是求这个数的几分之几是多少。
分数乘分数，用分子相乘的积作分子，用分母相乘的积作分母。
乘积是1的两个数互为倒数。
1的倒数是1，0没有倒数。
除以一个不等于0的数，等于乘这个数的倒数。
（一不变：被除数不变二变：除号变乘除数变为它的倒数）比的前项除以后项所得的商，叫做比值。
比值通常用分数表示，也可以用小数或整数表示，不能带单位。
比的前项和后项同时乘或除以相同的数（0除外），比值不变。
比的前项=后项×比值比的后项=前项÷比值工作总量÷工作效率和=工作时间路程÷相遇时间=速度和（a×b）×c=a×（b×c）乘法交换律（a+b）×c=ac=bc 乘法分配律ac+bc=（a+b）c 乘法分配律知道物体和距离和方向就能确定物体和位置。
（小于）（大于）一个因数小于1，积小于另一个因数。
除数小于1，商大于被除数。
（大于）（小于）求一个数的几分之几是多少“1”已知“1”×几分之几=部分量“1”未知部分量÷几分之几=“1”甲比乙多（少）几分之几，求甲“1”已知…1”×（1+几分之几）=部分量“1”已知“1”+‟1”×几分之几=部分量已知一个数的几分之几是多少，求这个数找单位“1”用方程或具体量÷对应的分率=‟1”甲比乙多（少）几分之几，求乙“1”未知x×（1+几分之几）=具体量x+x×几分之几=具体量具体量÷（1+几分之几）=“1”“1”+几分之几求的是甲是乙的几分之几。
“1”×几分之几求的是甲比乙多（少）的部分。
进率1千米＝1000米1米＝10分米1分米＝10厘米 1米＝100厘米1厘米＝10毫米1米＝1000毫米 1平方千米＝100公顷1公顷＝10000平方米1平方米＝100平方分米1平方分米＝100平方厘米1吨＝1000千克 1千克＝1000克1时=60分 1分=60秒质数表2、3、 5 、 7 、 11 、13 、17 、19 、23 、29 、 31 、37 、41 、43、 47、 53、 59 、 61、 67 、71、 73 、79 、83、 89 、97分数化小数1/2=0.5 4/1=0.25 4/3=0.75 1/5=0.2 2/5=0.4 3/5=0.6 4/5=0.8 1/8=0.1253/8=0.375 5/8=0.625 7/8=0.875 1/20=0.15 7/20=0.35 9/20=0.45。
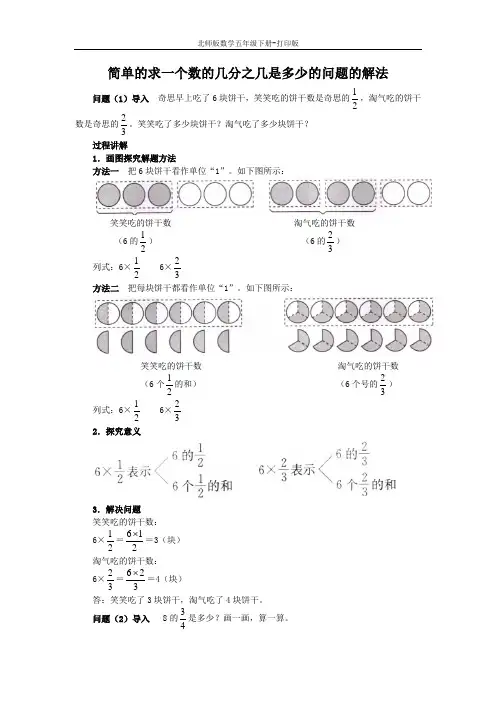
简单的求一个数的几分之几是多少的问题的解法问题（1）导入 奇思早上吃了6块饼干，笑笑吃的饼干数是奇思的21，淘气吃的饼干数是奇思的32。
笑笑吃了多少块饼干？淘气吃了多少块饼干？ 过程讲解1．画图探究解题方法方法一 把6块饼干看作单位“1”。
如下图所示：笑笑吃的饼干数 淘气吃的饼干数（6的21） （6的32） 列式：6×21 6×32方法二 把每块饼干都看作单位“1”。
如下图所示：笑笑吃的饼干数 淘气吃的饼干数（6个21的和） （6个号的32） 列式：6×21 6×322．探究意义3．解决问题笑笑吃的饼干数： 6×21＝216⨯＝3（块） 淘气吃的饼干数： 6×32＝326⨯＝4（块） 答：笑笑吃了3块饼干，淘气吃了4块饼干。
问题（2）导入 8的43是多少？画一画，算一算。
过程讲解1．画图探究解题方法方法一 把8看作单位“1”，平均分成4份，取其中的3份。
如下图所示：列式：8×43 方法二 把8看作8个单位“1”，把每个单位“1”都平均分成4份，取其中的3份。
如下图所示：列式：8×43 2．正确解答问题（3）导入 女生植了20棵树，男生植树的棵数比女生多41。
男生比女生多植树多少棵？ 过程讲解1．理解题意(1)分析题意，从“男生植树的棵数比女生多41”中可以知道，把女生植树的棵数看作单位“1”，男生比女生多植树的棵数占单位“1”的41。
(2)画方格图理解题意。
(3)明确解题思路。
求男生比女生多植树多少棵，就是求20的41是多少，用乘法计算。
2．列式解答答：男生比女生多植树5棵。
归纳总结 求一个数的几分之几是多少，用乘法计算，即用这个数乘几分之几。
第一单元分数乘法第二课一个数乘分数开心回顾【答案】C【解析】解：将计算问题与几何图形的面积计算相结合，通过练习提升学生综合运用知识的能力。
分析中应突出分步骤解答的思路，先求出宽，再根据公式计算面积。
2．的结果是。
【答案】6【解析】试题分析：一个分数乘整数的计算法则，用分子与整数相乘的积作分子，分母不变，能约分的先约分就比较简便。
解：===6；故答案为：6。
3．一辆小汽车每小时行54千米，小时行千米。
【答案】45【解析】试题分析：依据路程=速度×时间即可解答。
解：54×=45（千米），答：小时行45千米，故答案为：45。
4．10分米的是分米，1分米的是厘米，1元的是角。
【答案】7，2，8【解析】试题分析：根据一个数乘分数的意义：求这个数的几分之几是多少，用乘法解答。
解：10×=7（分米）1×=0.2（分米）=2（厘米）1×=0.8（元）=8（角）答：10分米的是7分米，1分米的是2厘米，1元的是8角。
故答案为：7，2，8。
5．小红体重135千克，小明的体重是小红体重的，小明体重多少千克？【答案】108千克【解析】试题分析：已知小明的体重是小红体重的，把小红的体重看作单位“1”，又知小红体重135千克，要求小明体重多少千克，就是求135的是多少，依据分数乘法意义即可解答。
解：135×=108（千克）答：小明体重108千克。
6．学校舞蹈队有60人，合唱队的人数是舞蹈队的，合唱队有多少人？【答案】45人【解析】试题分析：根据合唱队的人数是舞蹈队的，确定把舞蹈队的人数看作单位“1”，求合唱队有多少人，也就是求舞蹈队人数的是多少，根据一个数乘分数的意义，用乘法解答。
解：60×=45（人），答：合唱队有45人。
7．小华每天喝2杯这样的牛奶，他在整个九月份通过喝牛奶可以摄取钙质多少克？【答案】18克【解析】试题分析：该题中“一杯约250毫升的鲜牛奶”是多余条件，此外，九月份的天数“30天”是一个隐藏条件。
