第九章 第八节 棱柱与棱锥
- 格式:ppt
- 大小:2.60 MB
- 文档页数:62
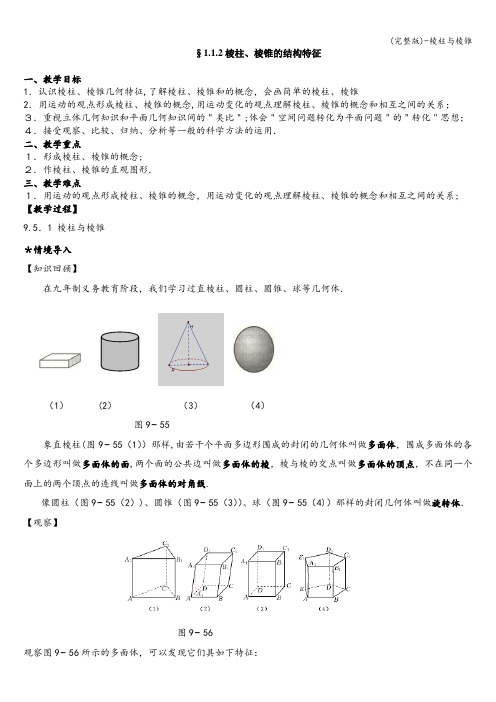
§1.1.2棱柱、棱锥的结构特征一、教学目标1.认识棱柱、棱锥几何特征,了解棱柱、棱锥和的概念,会画简单的棱柱、棱锥2.用运动的观点形成棱柱、棱锥的概念,用运动变化的观点理解棱柱、棱锥的概念和相互之间的关系;3.重视立体几何知识和平面几何知识间的"类比";体会"空间问题转化为平面问题"的"转化"思想;4.接受观察、比较、归纳、分析等一般的科学方法的运用.二、教学重点1.形成棱柱、棱锥的概念;2.作棱柱、棱锥的直观图形.三、教学难点1.用运动的观点形成棱柱、棱锥的概念,用运动变化的观点理解棱柱、棱锥的概念和相互之间的关系;【教学过程】9.5.1 棱柱与棱锥*情境导入【知识回顾】在九年制义务教育阶段,我们学习过直棱柱、圆柱、圆锥、球等几何体.(1) (2)(3)(4)图9−55象直棱柱(图9−55(1))那样,由若干个平面多边形围成的封闭的几何体叫做多面体,围成多面体的各个多边形叫做多面体的面,两个面的公共边叫做多面体的棱,棱与棱的交点叫做多面体的顶点,不在同一个面上的两个顶点的连线叫做多面体的对角线.像圆柱(图9−55(2))、圆锥(图9−55(3))、球(图9−55(4))那样的封闭几何体叫做旋转体.【观察】图9−56观察图9−56所示的多面体,可以发现它们具如下特征:(1)有两个面互相平行,其余各面都是四边形;(2)每相邻两个四边形的公共边互相平行.*引入新知有两个面互相平行,其余每相邻两个面的交线都互相平行的多面体叫做棱柱,互相平行的两个面,叫做棱柱的底面,其余各面叫做棱柱的侧面.相邻两个侧面的公共边叫做棱柱的侧棱.两个底面间的距离,叫做棱柱的高.根据棱柱的底面可以是三角形、四边形、五边形等这样的棱柱叫做三棱柱、四棱柱、五棱柱等图9−56所示的四个多面体都是棱柱.表示棱柱时,通常分别顺次写出两个底面各个顶点的字母,中间用一条短横线隔开,例如,图9−56(2)所示的棱柱,可以记作棱柱1111ABCD A B C D -,或简记作棱柱1AC .经常以棱柱底面多边形的边数来命名棱柱,如图9−56所示的棱柱依次为三棱柱、四棱柱、五棱柱. 侧棱与底面斜交的棱柱叫做斜棱柱,如图9−56(2);侧棱与底面垂直的棱柱叫做直棱柱,如图9−56(1);底面是正多边形的直棱柱叫做正棱柱,如图9−56(3)和(4),分别为正四棱柱和正五棱柱.正棱柱有下列性质:(1)侧棱垂直于底面,各侧棱长都相等,并且等于正棱柱的高;(2)两个底面中心的连线是正棱柱的高.例1。



第9章 B 第8讲时间:60分钟满分:100分一、选择题(8×5=40分)1.(2010·河北张家口调研)下列命题中,成立的是()A.各个面都是三角形的多面体一定是棱锥B.四面体一定是三棱锥C.棱锥的侧面是全等的等腰三角形,该棱锥一定是正棱锥D.底面多边形既有外接圆又有内切圆,且侧棱相等的棱锥一定是正棱锥解析:A是错误的,只要将底面全等的两个棱锥的底面重合在一起,所得多面体的每个面都是三角形,但这个多面体不是棱锥;B是正确的,三个面共顶点,另有三边围成三角形是四面体也必定是个三棱锥;C是错误的,如图所示,棱锥的侧面是全等的等腰三角形,但该棱锥不是正三棱锥;D也是错误的,底面多边形既有内切圆又有外接圆,如果不同心,则不是正多边形,因此不是正棱锥.答案:B2.在斜棱柱的侧面中,矩形最多有几个()A.2 B.3 C.4 D.6解析:最多2个,若有3个,则底面有三条边与侧棱垂直,而三边中至少有两条相交,即底面一定存在两相交直线与侧棱垂直,与斜棱柱定义矛盾.故选A.答案:A3.棱锥被平行于底面的平面所截,当截面分别平分侧棱、侧面积、体积时,相应截面面积分别为S1、S2、S3,则()A.S1<S2<S3B.S3<S2<S1C.S2<S1<S3D.S1<S3<S2解析:根据相似比知识易知(设底面为S4),①平分侧棱S1:S4=1:4,②平分侧面积S2:S4=1:2,③平分体积S 3:S 2=1:223,∴S 1<S 2<S 3.故选A. 答案:A4.(2010·湖北武汉六校高三第一次联考)正四棱锥S -ABCD 中,侧棱与底面所成的角为α,侧面与底面所成的角为β,侧面等腰三角形的底角为γ,相邻两侧面所成的二面角为θ,则α、β、γ、θ的大小关系是( )A .α<β<γ<θB .α<β<θ<γC .θ<α<γ<βD .α<γ<β<θ解析:依题意不妨设SA =AB =1,如图,α=∠SAO ,β=∠SEO ,γ=∠SBC =60°.过A 点作AF ⊥SB ,连结CF ,则∠AFC =θ. ∵cos α=22,cos β=OE SE =33,cos γ=12,cos θ=-13, ∴α<β<γ<θ.故选A. 答案:A5.正六棱锥P -ABCDEF 中,G 为PB 的中点,则三棱锥D -GAC 与三棱锥P -GAC 体积之比为( )A .1∶1B .1∶2C .2∶1D .3∶2解析:如图,设棱锥的高为h ,V D -GAC =V G -DAC =13S △ADC ·12h ,V P -GAC =12V P -ABC =V G -ABC=13S △ABC ·h 2. 又S △ADC S △ABC =2∶1,故V D -GAC ∶V P -GAC =2∶1. 答案:C6.所有棱长都是a 的四棱柱ABCD -A 1B 1C 1D 1,对角线AC 1、BD 1、B 1D 两两垂直,则侧棱与底面所成的角为( )A .90°B .arccos 13C .arccos33D .60°解析:本题是关于立体几何中的线面角内容问题,由条件可知侧棱与底面所成的角即为∠AA 1C 1,由已知B 1D ⊥BD 1可得四边形B 1BDD 1为菱形,且底面边长为a ,∠D 1A 1B 1=60°,从而A 1C 1=3a ,又由条件可知AC 1⊥面B 1BDD 1,从而有AC 1⊥AA 1, 故在Rt △A 1AC 1中,易知cos ∠AA 1C 1=a 3a =33, ⇒∠AA 1C 1=arccos 33,从而选C. 答案:C7.如图,在正三棱锥A -BCD 中,E 、F 分别是AB 、BC 的中点,EF ⊥DE .若BC =a ,则A -BCD 的体积为( )A.224a 3B.212a 3C.324a 3 312a 3 解析:∵三棱锥A -BCD 为正三棱锥, ∴AC ⊥BD .又点E 、F 分别是AB 、BC 的中点. ∴EF ∥AC .由EF ⊥DE 可得AC ⊥DE . ∴AC ⊥平面ABD ,则AC ⊥AB 且AC ⊥AD , 从而得AB ⊥AD ,即正三棱锥的三个侧面均为等腰直角三角形. 由BC =a 可得AB =AC =AD =22a , V 正棱锥A -BCD =16(22a )3=224a 3,故应选A.答案:A8.(2010·湖北八校第二次联考)如图,正方体AC 1的棱长为1,连结AC 1,交平面A 1BD于H ,则以下命题中,错误的命题是()A .AC 1⊥平面A 1BDB .H 是△A 1BD 的垂心C .AH =33D .直线AH 和BB 1所成的角为45°解析:由⎭⎪⎬⎪⎫AC 1⊥DAC 1⊥BA 1BD ∩BA 1=B ⇒AC 1⊥面A 1BD ,故A 为真命题. 正三棱锥A -BA 1D 中,因AB ⊥AD ⊥AA 1,则A 在底面BA 1D 的射影为三角形的垂心,故B 为真命题.由V A -BA 1D =V D -ABA 1,可知 13S △BA 1D ·|AH |=13·12|AB ||AA 1|·|AD |, 则|AH |=33,故C 为真命题. 因BB 1∥AA 1,则BB 1与AH 所成的角为∠A 1AC 1=arctan 2≠45°,故D 为假命题. 答案:D二、填空题(4×5=20分)9.(2010·黄冈一模)已知正四棱锥的体积为12,底面对角线的长为26,则侧面与底面所成的二面角等于____________.解析:如图所示,设底面边长为a ,则2a 2=(26)2,∴a =23,∴OM = 3. 又V =13·(23)2·h =12,∴h =3.∴tan ∠VMO =33=3, ∴∠VMO =π3.∴侧面与底面所成的二面角为π3.答案:π310.如图,在直四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 是菱形,∠BAD =60°,AA 1=AB =1,则截面ACC 1A 1的面积为________,异面直线AD 与D 1C 所成角的余弦值为________.解析:截面ACC 1A 1为矩形, AA 1=1,AC =3,其面积S =3; BD =1,BD 1=2,在△BCD 1中,BC =1, CD 1=2,cos ∠BCD 1=24. 则异面直线AD 与D 1C 所成角的余弦值为24. 答案:32411.如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为2,点E 是正方形BCC 1B 1的中心,点F 、G 分别是棱C 1D 1、AA 1的中点.设点E 1、G 1分别是点E 、G 在平面DCC 1D 1内的正投影.则以E 为顶点,以四边形FGAE 在平面DCC 1D 1内的正投影为底面边界的棱锥的体积为________.解析:点A 、E 、G 、F 在平面DCC 1D 1的投影分别为点D 、E 1、G 1、F ,连结EF 、EE 1、EG 1、ED ,则V E -DE 1FG 1=V F -EE 1G 1+V D -EE 1G 1=13×1×1+13×1×1=23.答案:2312.如图,在直三棱柱ABC —A 1B 1C 1中,AB =BC =2,BB 1=2,∠ABC =90°,E 、F 分别为AA 1、C 1B 1的中点,沿棱柱的表面从E 到F 两点的最短路径的长度为________.解析:∵AB =BC =2,∠ABC =90°,∴AC =2, ∴侧面展开后如下图所示.A 1E =12AA 1=1,A 1F =A 1B 1+B 1F =322,∴EF =A 1E 2+A 1F 2=1+92=222. 把△A 1B 1C 1与侧面A 1B 1BA 展开如右图所示. 连结EF ,过E 作EM ⊥B 1B , 则EM =AB =2,FM =1+22, ∴EF =72+2, 若把△A 1B 1C 1与侧面A 1ACC 1展开如右图. 连结EF ,作EM ⊥CC 1于M ,作FD ⊥EM 于D 点, 则ED =32,FD =32,∴EF =(32)2+(32)2=322. 比较以上三条路径,第三条最小,∴EF 间最短路径为322.答案:322三、解答题(4×10=40分)13.(2009·陕西高考)如图,在直三棱柱ABC -A 1B 1C 1中,AB =1,AC =AA 1=3,∠ABC =60°.(1)求证:AB ⊥A 1C ;(2)求二面角A -A 1C -B 的大小.思路点拨:第(1)问可先证AB ⊥面ACC 1A 1,第(2)问作AD ⊥A 1C 于点D ,结合(1),知∠ADB 即为所求二面角的平面角.亦可利用空间向量坐标法解决.解析:解法一:(1)证明:∵三棱柱ABC -A 1B 1C 1为直三棱柱,∴AB ⊥AA 1. 在△ABC 中,AB =1,AC =3,∠ABC =60°, 由正弦定理得∠ACB =30°, ∴∠BAC =90°,即AB ⊥AC .∴AB ⊥平面ACC 1A 1.又A 1C ⊂平面ACC 1A 1, ∴AB ⊥A 1C .(2)如图,作AD ⊥A 1C 交A 1C 于D 点,连结BD .由三垂线定理知BD ⊥A 1C ,∴∠ADB 为二面角A -A 1C -B 的平面角. 在Rt △AA 1C 中,AD =AA 1·AC A 1C =3×36=62,在Rt △BAD 中,tan ∠ADB =AB AD =63, ∴∠ADB =arctan63, 即二面角A -A 1C -B 的大小为arctan63. 解法二:(1)证明:∵三棱柱ABC -A 1B 1C 1为直三棱柱, ∴AA 1⊥AB ,AA 1⊥AC .在△ABC 中,AB =1,AC =3,∠ABC =60°, 由正弦定理得∠ACB =30°, ∴∠BAC =90°,即AB ⊥AC . 如图,建立空间直角坐标系,则A (0,0,0),B (1,0,0),C (0,3,0),A 1(0,0,3), ∴AB →=(1,0,0),A 1C →=(0,3,-3). ∵AB →·A 1C →=1×0+0×3+0×(-3)=0, ∴AB ⊥A 1C .(2)如图,可取m =AB →=(1,0,0)为平面AA 1C 的法向量,设平面A 1BC 的法向量为n =(l ,m ,n ),则BC →·n =0,A 1C →·n =0, 又BC →=(-1,3,0),∴⎩⎨⎧-l +3m =0,3m -3n =0.∴l =3m ,n =m .不妨取m =1,则n =(3,1,1). cos 〈m ,n 〉=m ·n |m ||n |=3×1+1×0+1×0(3)2+12+12·12+02+02=155, ∴二面角A -A 1C -B 的大小为arccos155. 14.如图,在四棱锥P —ABCD 中,P A ⊥底面ABCD ,∠DAB 为直角,AB ∥CD ,AD =CD =2AB ,E 、F 分别为PC 、CD 的中点.(1)求证:CD ⊥平面BEF ;(2)设P A =k ·AB ,且二面角E -BD -C 的平面角大于30°,求k 的取值范围.解析:(1)证明:如图,由已知DF 綊AB 且∠DAB 为直角,故ABFD 是矩形.从而CD ⊥BF . 又P A ⊥底面ABCD ,CD ⊥AD ,故由三垂线定理知CD ⊥PD . 在△PDC 中,E 、F 分别为PC 、CD 的中点. 故EF ∥PD ,从而CD ⊥EF , 由此得CD ⊥面BEF .(2)连结AC 交BF 于G ,易知G 为AC 的中点.连结EG .则在△P AC 中易知EG ∥P A .又因P A ⊥底面ABCD ,故EG ⊥底面ABCD .在底面ABCD 中,过G 作GH ⊥BD ,垂足为H ,连结EH .由三垂线定理知EH ⊥BD .从而∠EHG 为二面角E -BD -C 的平面角.设AB =a ,则在△P AC 中,有EG =12P A =12ka .以下计算GH .考虑底面的平面图(如右图). 连结GD ,因S △GBD =12BD ·GH =12GB ·DF ,故GH =GB ·DFBD.在△ABD 中,因AB =a ,AD =2a ,得BD =5a . 而GB =12FB =12AD =a ,DF =AB ,从而得GH =GB ·AB BD =a ·a 5a =55a .因此tan ∠EHG =EG GH =12ka 55a =52k .由k >0知∠EHG 是锐角,故要使∠EHG >30°, 必须52k >tan30°=33, 解之,得k 的取值范围是k >21515.解法二:(1)如图,以A 为原点,AB 所在直线为x 轴,AD 所在直线为y 轴,AP 所在直线为z 轴建立空间直角坐标系,设AB =a ,则易知点A、B 、C 、D 、F 的坐标分别为A (0,0,0)、B (a,0,0)、C (2a,2a,0)、D (0,2a,0)、F (a,2a,0).从而DC →=(2a,0,0),BF →=(0,2a,0),DC →·BF →=0.故DC →⊥BF →. 设P A =b ,则P (0,0,b ),而E 为PC 中点. 故E (a ,a ,b 2).从而BE →=(0,a ,b 2).DC →·BE →=0,故DC →⊥BE →.由此得CD ⊥面BEF .(2)设E 在xOy 平面上的投影为G ,过G 作GH ⊥BD 垂足为H .由三垂线定理知EH ⊥BD .从而∠EHG 为二面角E -BD -C 的平面角.由P A =k ·AB 得P (0,0,ka ),E (a ,a ,ka 2),G (a ,a,0).设H (x ,y,0),则GH →=(x -a ,y -a,0),BD →=(-a,2a,0), 由GH →·BD →=0得-a (x -a )+2a (y -a )=0, 即x -2y =-a .①又因BH →=(x -a ,y,0),且BH →与BD →的方向相同, 故x -a -a =y2a,即2x +y =2a .② 由①②解得x =35a ,y =45a .从而GH →=(-25a ,-15a,0),|GH →|=55a .tan ∠EHG =|EG →||GH →|=ka 255a =52k .由k >0知∠EHG 是锐角,由∠EHG >30°, 得tan ∠EHG >tan30°,即52k >33. 故k 的取值范围为k >21515.15.(2010·四川攀枝花三模)如图所示,四棱锥P -ABCD 的底面为直角梯形,∠ADC =∠DCB =90°,AD =1,BC =3,PC =CD =2,PC ⊥底面ABCD ,E 为AB 的中点.(1)求证:平面PDE ⊥平面P AC ;(2)求二面角C -PD -E 的大小;(3)求点B 到平面PDE 的距离.解析:解法一:(1)证明:设AC 与DE 交点为G ,延长DE 交CB 的延长线于点F , 则△DAE ≌△FBE ,∴BF =AD =1.∴CF =4.∴tan ∠F =DC CF =12. 又∵tan ∠ACD =AD DC =12,∴∠F =∠ACD .又∵∠ACD +∠ACF =90°,∴∠F +∠ACF =90°.∴∠CGF =90°.∴AC ⊥DE .又∵PC ⊥底面ABCD ,∴PC ⊥DE .∴DE ⊥平面P AC .∵DE ⊂平面PDE ,∴平面PDE ⊥平面P AC .(2)连结PG ,过点C 作CH ⊥PG 于H 点,取PD 中点I ,连结CI ,易知CI ⊥PD .又由(1)知平面PDE ⊥平面P AC ,且PG 是交线,根据面面垂直的性质,得CH ⊥平面PDE ,由三垂线定理知HI ⊥PD .从而∠CIH 为二面角C -PD -E 的平面角.在等腰Rt △PCD 中,CI =22PC =2, 在Rt △DCA 中,CG =CD 2AC =2222+12=455, 在Rt △PCG 中,CH =PC ·CG PG =PC ·CG PC 2+CG 2=2×455655=43, 从而sin ∠CIH =CH CI =223,则∠CIH =arcsin 223., 即二面角C -PD -E 的大小为arcsin 223.(3)由于BF =14CF ,∴可知点B 到平面PDE 的距离等于点C 到平面PDE 的距离的14,即14CH .在Rt △PCG 中,CH =PC ·CG PC 2+CG 2=2×45522+(455)2=43, 从而点B 到平面PDE 的距离等于13. 解法二:如图所示,以点C 为坐标原点,直线CD ,CB ,CP 分别为x ,y ,z 轴,建立空间直角坐标系C -xyz ,则相关点的坐标为C (0,0,0),A (2,1,0),B (0,3,0),P (0,0,2),D (2,0,0),E (1,2,0).(1)证明:由于DE →=(-1,2,0),CA →=(2,1,0),CP →=(0,0,2),∴DE →·CA →=(-1,2,0)·(2,1,0)=0,DE →·CP →=(-1,2,0)·(0,0,2)=0.∴DE ⊥CA ,DE ⊥CP .而CP ∩CA =C ,∴DE ⊥平面P AC .∵DE ⊂平面PDE ,∴平面PDE ⊥平面P AC .(2)设n =(x ,y ,z )是平面PDE 的一个法向量,则n ·DE →=n ·PE →=0,由于DE →=(-1,2,0),PE →=(1,2,-2),∴有⎩⎪⎨⎪⎧n ·DE →=(x ,y ,z )·(-1,2,0)=-x +2y =0,n ·PE →=(x ,y ,z )·(1,2,-2)=x +2y -2z =0. 令x =2,则y =1,z =2.即n =(2,1,2),易知平面PCD 的一个法向量m =(0,1,0),cos 〈m ,n 〉=m ·n |m ||n |=13, ∴二面角C -PD -E 的大小为arccos 13. (3)由(2)知n =(2,1,2)是平面PDE 的一个法向量,而BE →=(1,-1,0),∴点B 到平面PDE 的距离为d =|n ·BE →||n |=|(2,1,2)·(1,-1,0)|3=13. 16.(2010·河北唐山二模)如图,在直三棱柱ABC -A 1B 1C 1中,∠ABC =90°,AB =BC =2,AA 1=4,M 、N 分别为CC 1、A 1C 1的中点.(1)求证:AM ⊥平面B 1MN ;(2)求二面角A 1-B 1M -A 的大小.解析:解法一:(1)证明:∵ABC -A 1B 1C 1是直三棱柱, ∴平面A 1B 1C 1⊥平面A 1ACC 1,∵AB =BC ,进而A 1B 1=B 1C 1,N 为A 1C 1的中点,∴B 1N ⊥平面A 1ACC 1,∵AM ⊂平面A 1ACC 1,∴B 1N ⊥AM ,即AM ⊥B 1N . 在侧面A 1ACC 1中,C 1M =CM =2,C 1N =2,AC =22, ∴Rt △MC 1N ∽Rt △ACM ,∴∠C 1MN +∠CMA =90°. ∴AM ⊥MN .∵B 1N ∩MN =N ,∴AM ⊥平面B 1MN .(2)分别取AB 1、B 1M 、A 1M 的中点为D 、E 、F ,连结△DEF ,则DE ∥AM 、EF ∥A 1B 1.由(1),AM ⊥平面B 1MN ,而B 1M ⊂平面B 1MN ,则AM ⊥B 1M ,于是DE ⊥B 1M ,∵A 1B 1⊥B 1C 1,A 1B 1⊥B 1B ,B 1C 1∩B 1B =B 1,∴A 1B 1⊥平面B 1BCC 1.∵B 1M ⊂平面B 1BCC 1,∴A 1B 1⊥B 1M .于是EF ⊥B 1M . 所以∠DEF 为二面角A 1-B 1M -A 的平面角.连结A 1B 、BM ,DE 、EF 、FD 分别为△AB 1M 、△A 1MB 1、△MA 1B 的中位线. ∵A 1B 1⊥平面B 1BCC 1,BM ⊂平面B 1BCC 1,A 1B 1⊥BM , ∴EF ⊥BM ,EF ⊥FD .在Rt △DEF 中,EF =12A 1B 1=1,FD =12BM =2, ∴tan ∠DEF =FD EF =2,∠DEF =arctan 2.故二面角A 1-B 1M -A 的大小为arctan 2. 解法二:(1)证明:分别以BA 、BB 1、BC 为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系B -xyz ,则A (2,0,0),M (0,2,2),B 1(0,4,0),N (1,4,1).∵AM →=(-2,2,2),B 1N →=(1,0,1), B 1M →=(0,-2,2),∴AM →·B 1N →=AM →·B 1M →=0.∴AM ⊥B 1N ,AM ⊥B 1M ,又B 1N ∩B 1M =B 1,∴AM ⊥平面B 1MN .(2)由(1)知,AM ⊥平面B 1MN , ∵B 1M ⊂平面B 1MN ,∴AM ⊥B 1M . ∵A 1B 1⊥B 1C 1,A 1B 1⊥B 1B ,B 1C 1∩B 1B =B 1, ∴A 1B 1⊥平面B 1BCC 1.∵B 1M ⊂平面B 1BCC 1,∴A 1B 1⊥B 1M . ∵MA →=(2,-2,-2),B 1A 1→=(2,0,0),∴cos 〈MA →,B 1A 1→〉=MA →·B 1A 1→|MA →||B 1A 1→|=33. 故二面角A 1-B 1M -A 的大小为arccos 33.。

