虚功原理复习与例题
- 格式:ppt
- 大小:632.00 KB
- 文档页数:50
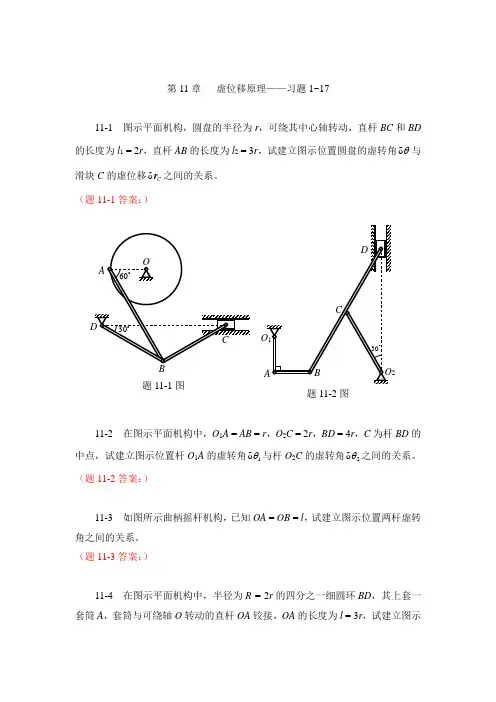
第11章 虚位移原理——习题1~1711-1 图示平面机构,圆盘的半径为r ,可绕其中心轴转动,直杆BC 和BD 的长度为l 1 = 2r ,直杆AB 的长度为l 2 = 3r ,试建立图示位置圆盘的虚转角θδ与滑块C 的虚位移C r δ之间的关系。
(题11-1答案:)11-2 在图示平面机构中,O 1A = AB = r ,O 2C = 2r ,BD = 4r ,C 为杆BD 的中点,试建立图示位置杆O 1A 的虚转角1δθ与杆O 2C 的虚转角2δθ之间的关系。
(题11-2答案:)11-3 如图所示曲柄摇杆机构,已知OA = OB = l ,试建立图示位置两杆虚转角之间的关系。
(题11-3答案:)11-4 在图示平面机构中,半径为R = 2r 的四分之一细圆环BD ,其上套一套筒A ,套筒与可绕轴O 转动的直杆OA 铰接,OA 的长度为l = 3r ,试建立图示题11-1图题11-2图位置杆OA 的虚转角与点D 的虚位移之间的关系。
(题11-4答案:)11-5 在如图所示平面机构中,O 1A = O 3C = O 3D = AB = l ,在图示位置,CB = O 2B =l 332,试建立该位置A 、D 两点虚位移之间的关系。
(题11-5答案:)11-6 在图示平面机构中,ABD 为边长等于a 的正三角形平板,O 1B 、O 2D 的杆长也均为a 。
机构在图示位置时,杆OE 与水平线成60◦角,A 、D 、O 2在同一水平线上,O 1B 位于铅垂位置,且OA = a ,试求此瞬时刚体O 1B 与OE 的虚转角之间的关系。
题11-3图题11-4图题11-5图题11-6图(题11-6答案:)11-7 在图示平面四连杆机构中,在杆AB 上垂直地作用有三角形分布载荷,其最大集度为q ,在杆OA 的中点作用有水平向左的主动力F ,且F = ql ,若不计各构件自重和各接触处摩擦,为使系统在图示位置平衡,所需施加的作用于杆BC 上的主动力偶矩M 的值。


高中物理专题:相互作用——自招(含答案)一.知识点1.重心2.摩擦角、自锁区3.力矩4.平衡的种类与条件(共点力平衡、定轴平衡、刚体平衡)5.虚功原理二.典例解析1.重心【例1】(•同济)如图(a)所示,一根细长的硬棒上有3个小球,每个小球之间相距a,小球质量为m、2m和3m,棒的质量分布均匀,总长为4a,质量为4m,求整个体系的重心位置。
变式1:均匀圆板的半径为R,在板内挖去一个半径为r的小圆,两个圆心相距为a,求剩余部分的重心与原圆板圆心的距离变式2:求三角板与三角框的重心O arO1R匀质三角板的重心在哪?匀质三角框的重心在哪?2.摩擦力、摩擦角、自锁区【例2】一个质量m=20kg的钢件,架在两根完全相同的、平行的长直圆柱上,如图所示,钢件的重心与两柱等距,两柱的轴线在同一水平面内,圆柱的半径r=0.025m,钢件与圆柱间的滑动摩擦系数μ=0.20,两圆柱各绕自己的轴线做转向相反的转动,角速度ω=40rad/s,若沿平行于柱轴方向施加力推着钢件做速度为v0=0.05m/s的匀速运动,推力是多大?设钢件左右受光滑槽限制(图中未画出),不发生横向运动.g取10m/s2.【例3】(华约)明理同学平时注意锻炼身体,力量较大,最多能提起m=50kg的物体。
一重物放置在倾角θ=15°的粗糙斜坡上,重物与斜坡间的摩擦因数为μ=3≈0.58。
试求该同学向上拉动的重物质量M的最大值?【变式】如图所示,AOB是一把等臂夹子,轴O处的摩擦不计,若想在A、B处用力去夹一个圆形物体C,则能否夹住与那些因素有关?这些因素应该满足什么条件?(不考虑圆柱形物体受到的重力)3.力矩【例4】(清华大学)如图,一根光滑均匀细棒质量为m,一端通过光滑铰链固定在地上,另θ,现使方形一端搁在方形木块上,初始时细棒和地面夹角为︒=30木块很缓慢地向正左方运动,则细棒在竖直面内转动的过程中,受到木块的作用力:A.一直增大B.一直减小C.先增大后减小D.先减小后增大【变式1】(复旦)一根轻杆下端与一个半径为R,重力为G的光滑球相连,杆上段可绕轴O 自由转动,杆长L,杆与球始终在同一直线上,O点还挂有一根系有重物的细绳,如图所示,重物的重力为G′,则平衡后杆与竖直方向的夹角α【变式2】(•西安交大)重为80kg的人沿如图所示的梯子从底部向上攀登,梯子质量为25kg,顶角为30°。

虚功原理(物理竞赛)§2、虚功原理上次课主要是介绍了分析力学中经常要用到的一些基本概念,并由虚功的概念和理想约束的概念导出了解决静力学问题的虚功原理:0=⋅∑i r i F δ。
虚功原理适用的范围是:质点组,它适用的前提条件是只受理想约束。
这次课就举一些具体例子,使我们能够了解如何利用虚功原理去解决静力学问题。
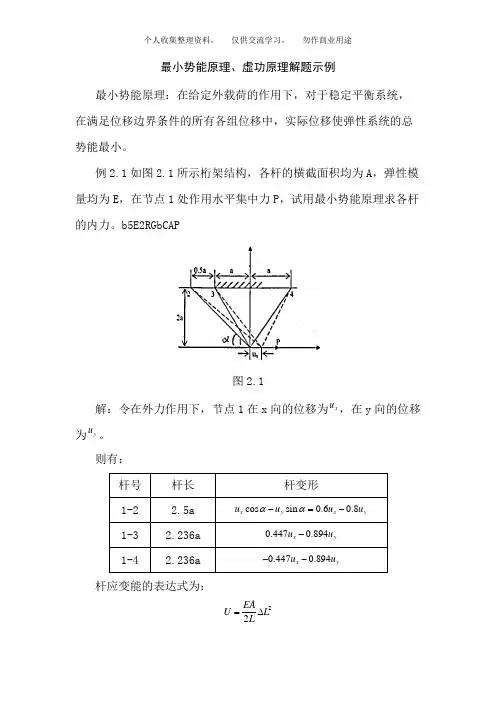
三、应用虚功原理解题:例1、如图所示,有一质量为m ,长度为 的刚性杆子,靠在墙上,在与地面接触的B 端上受一水平向左的外力F ,杆子两端的接触都是光滑的,当杆子与水平地面成α角时,要使杆子处于平衡状态,问作用在杆子B 端上的力F 有多大?求F =?解:由题意可知它是一个静力学问题,而且接触都是光滑的,显然可以应用虚功原理来求解这个问题。
这个例子很简单,简单的题目往往能够清楚地说明物理意义,为了说明虚功原理的意义,如果一开始就举复杂的例子,由于复杂的数字计算将会掩盖物理意义,所以就以这个简单的例子来看看如何应用虚功原理来解出它。
第一步当然也是确定研究对象,即①选系统:在这个例题中,我们就取杆子为应用虚功原理的力学系统。
②找主动力:作用在我们所选取的系统上的主动力有几个?有两个。
一个是水平作用力F ,还有一个是重力m g 作用在杆子的质心上。
因为杆子两端A 、B 处的接触是光滑的,∴在该两处的约束力也就不必考虑。
③列出虚功方程:主动力找出来以后,视计算方便起见,适当选好坐标,并根据虚功原理列出虚功方程。
现在选取如图所示的直角坐标,于是我们现在就可列出系统的虚功方程。
列虚功方程时,正、负号是个很重要的问题,如果按虚位移的实际方向与力的方向间的关系确定虚功的正负号,很容易弄错。
为了不容易弄错,我们还是按力的作用点的坐标的正方向与力的方向间的关系来确定虚功的正负号。
这种方法既方便而又不容易搞错。
在列方程时必须要注意这个问题。
∵F 的方向与其作用点的坐标X 的正方向相反,∴F 取负而δX B 取正,∴此力的虚功为负的,即:0=--C B y mg x F δδ……①,由于虚功方程中的两个虚位移不是相互独立的,∴我们还需要将它们化成独立变量,然后才能令独立虚位移前的乘数等于零,从而求出最后的结果。

§2、虚功原理上次课主要是介绍了分析力学中经常要用到的一些基本概念,并由虚功的概念和理想约束的概念导出了解决静力学问题的虚功原理:0=⋅∑i r i F δ。
虚功原理适用的范围是:质点组,它适用的前提条件是只受理想约束。
这次课就举一些具体例子,使我们能够了解如何利用虚功原理去解决静力学问题。
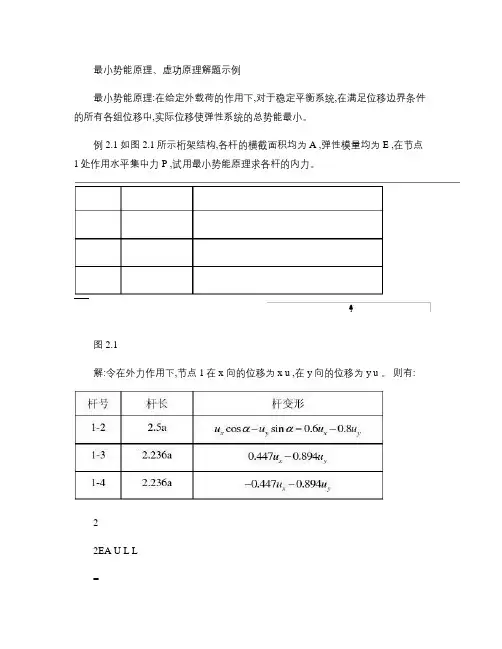
三、应用虚功原理解题:例1、如图所示,有一质量为m ,长度为 的刚性杆子,靠在墙上,在与地面接触的B 端上受一水平向左的外力F ,杆子两端的接触都是光滑的,当杆子与水平地面成α角时,要使杆子处于平衡状态,问作用在杆子B 端上的力F 有多大?求F =?解:由题意可知它是一个静力学问题,而且接触都是光滑的,显然可以应用虚功原理来求解这个问题。
这个例子很简单,简单的题目往往能够清楚地说明物理意义,为了说明虚功原理的意义,如果一开始就举复杂的例子,由于复杂的数字计算将会掩盖物理意义,所以就以这个简单的例子来看看如何应用虚功原理来解出它。
第一步当然也是确定研究对象,即①选系统:在这个例题中,我们就取杆子为应用虚功原理的力学系统。
②找主动力:作用在我们所选取的系统上的主动力有几个?有两个。
一个是水平作用力F ,还有一个是重力m g 作用在杆子的质心上。
因为杆子两端A 、B 处的接触是光滑的,∴在该两处的约束力也就不必考虑。
③列出虚功方程:主动力找出来以后,视计算方便起见,适当选好坐标,并根据虚功原理列出虚功方程。
现在选取如图所示的直角坐标,于是我们现在就可列出系统的虚功方程。
列虚功方程时,正、负号是个很重要的问题,如果按虚位移的实际方向与力的方向间的关系确定虚功的正负号,很容易弄错。
为了不容易弄错,我们还是按力的作用点的坐标的正方向与力的方向间的关系来确定虚功的正负号。
这种方法既方便而又不容易搞错。
在列方程时必须要注意这个问题。
∵F 的方向与其作用点的坐标X 的正方向相反,∴F 取负而δX B 取正,∴此力的虚功为负的,即:0=--C B y mg x F δδ……①,由于虚功方程中的两个虚位移不是相互独立的,∴我们还需要将它们化成独立变量,然后才能令独立虚位移前的乘数等于零,从而求出最后的结果。



§2、虚功原理上次课主要是介绍了分析力学中经常要用到的一些基本概念,并由虚功的概念和理想约束的概念导出了解决静力学问题的虚功原理:0=⋅∑i r i F ρϖδ。
虚功原理适用的范围是:质点组,它适用的前提条件是只受理想约束。
这次课就举一些具体例子,使我们能够了解如何利用虚功原理去解决静力学问题。
三、应用虚功原理解题:例1、如图所示,有一质量为m ,长度为λ的刚性杆子,靠在墙上,在与地面接触的B 端上受一水平向左的外力F ρ,杆子两端的接触都是光滑的,当杆子与水平地面成α角时,要使杆子处于平衡状态,问作用在杆子B 端上的力F ρ有多大求F ρ=解:由题意可知它是一个静力学问题,而且接触都是光滑的,显然可以应用虚功原理来求解这个问题。
这个例子很简单,简单的题目往往能够清楚地说明物理意义,为了说明虚功原理的意义,如果一开始就举复杂的例子,由于复杂的数字计算将会掩盖物理意义,所以就以这个简单的例子来看看如何应用虚功原理来解出它。
第一步当然也是确定研究对象,即①选系统:在这个例题中,我们就取杆子为应用虚功原理的力学系统。
②找主动力:作用在我们所选取的系统上的主动力有几个有两个。
一个是水平作用力F ρ,还有一个是重力m g ρ作用在杆子的质心上。
因为杆子两端A 、B 处的接触是光滑的,∴在该两处的约束力也就不必考虑。
③列出虚功方程:主动力找出来以后,视计算方便起见,适当选好坐标,并根据虚功原理列出虚功方程。
现在选取如图所示的直角坐标,于是我们现在就可列出系统的虚功方程。
列虚功方程时,正、负号是个很重要的问题,如果按虚位移的实际方向与力的方向间的关系确定虚功的正负号,很容易弄错。
为了不容易弄错,我们还是按力的作用点的坐标的正方向与力的方向间的关系来确定虚功的正负号。
这种方法既方便而又不容易搞错。
在列方程时必须要注意这个问题。
∵F ρ的方向与其作用点的坐标X 的正方向相反,∴F 取负而δX B 取正,∴此力的虚功为负的,即:0=--C B y mg x F δδ……①,由于虚功方程中的两个虚位移不是相互独立的,∴我们还需要将它们化成独立变量,然后才能令独立虚位移前的乘数等于零,从而求出最后的结果。
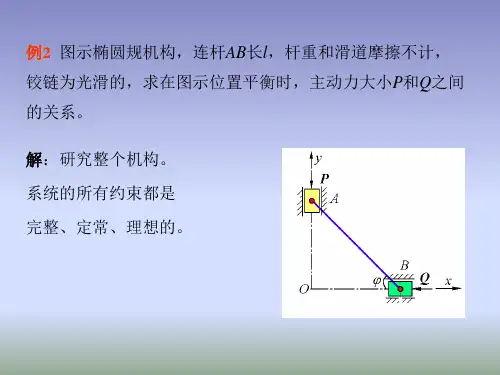
虚功原理解题步骤分析约束,确定自由度选好广义坐标写出主动力作用点的坐标并对其变分代入虚功原理公式中求解Attention:静系中的平衡只有广义坐标方可独立变化虚功原理中不出现约束力)(t q r r rr =正确写出原理求棒全长。
yxmgα分析自由度数目1xmgBDαsin )(l C −=αc 0]sin 2cos )2cos 2[(2=−−δααααa l a mg]sin 2cos )2cos 2[(2−−δααααa l a mg !!!0≠δαQ ααcos )1cos 2(42−=∴a l αcos 2a ca c l )2(422−=∴0=αsin )(AC AD y c −=ααsin )2cos 2(l a −=∂∂αcr r r ααq r F Q i ii ∂∂•=∑r r 2l 0]sin 2cos )2cos 2[(=−−αααa l a mgrABFr y分析自由度2广义坐标βα,βDdemonstrationgm r gm rαsin 2l y =βαsin 2sin l l y +=2l 2l BD C x F y mg y mg w δδδδ++=)sin (sin βδβαδα+−l2l δ2l l y =)βδβδβββδαα)sin cos 2()sin 23Fl mg l l −+0=δβββ)sin cos (23Fl mg l l −0=!!!0≠可任意变化且和δβδαQ 23αl 0)sin cos 2(=−ββFl mg l23l 2−l F mg 23αF2c Q =j mg Fd i F F B =l j lα2sin 2+l l i l r r 2sin ()cos 2αβ++ααq r F Q iii ∂∂•=∑r r ααα∂•+∂•+∂•=B B D D c c F F F r r r 0sin cos 23=−=ααFl mgll j lα2sin 2+j l l i l l r r r r sin 2sin ()cos 2cos (αβα+++=i l l r r r)cos cos (βα++=βββ∂+∂+∂Bd c F mg δββ2l 0=Fmg tg 2=β试用虚功原理求平衡菱形的顶角为2α,一重为W的重物,C点系yTr分析自由度广义坐标α?!!!解除一个约束一个自由度Wααactg l yc −=cos 2αc D =0=0]cos =δαα0≠可任意变化且δαQ )csc sin 2(cos 22αααa l l w T −=yxθ),(y x B ),(c c y x c 定曲面上,如果杆在与竖直墙间的夹角< 的任意位置均能平衡,试求曲面形状.2π2l δ2l y −=???=δθθδd dy y =))((θx y y =c 2(−θld 0≠δθQ 2−∴θld dy 02=−∴θl d dx dx θsin l x =Qθd dx ∴2−∴θl d dx dx θd dx2222x l x l tg l dx −==θx l −22212l 22212xl l y −−=1)2()2(2222=−+l l y l xMrr ABCl l 43ll 411x 2x 3x 取广义坐标为)(33211x x x q ++=)(21312x x q −=)2(313213x x x q +−=求相应广义力???===Q Q Q '3F r r 2F lM F l M F FF F F r r r r rr r r −===='33214143)2('x F x F x F x F W δδδδδr r r r Q +++=)(1x x x q ++=321121q q q x δδδδ++=312q q x δδδ−=321321q q q x δδδδ+−=)3()2381()43(321q l M F q lM F q F W δδδδ++−+=Q MF Q F Q 3−==。