当前位置：文档之家 › 虚位移原理例题

虚位移原理例题

  • 格式：pptx
  • 大小：1.91 MB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

第17章 虚位移原理

第17章 虚位移原理


(e) (e) 动量定理 或 dK F 或 MaC F 质心运动定理 dt dLO mO ( F ) 0 动量矩定理 mO ( F ) dt
(e) F 0
还是静 力学方 程，无 意义。
2
动能定理
假设系统有一小的位移
dT 0
质点系自由度 ＝ 自由质点系自由度 — 约束（方程）数
2. 以刚体作为基本单元 自由刚体系：OA、AB；自由度 ＝ 3×2 ＝ 6 约束方程： 约束数 ＝ 5
xO 0, x A x A , yO 0, y A y A , yB 0
O
y
A
r
A
l

B
x
质点系自由度 ＝ 6 — 5 ＝ 1 质点系自由度 ＝ 自由刚体系自由度 — 约束（方程）数
注1：通常两种方法各有侧重，有些问题用几何法容易，有些问题用解析
法容易。一般容易作运动学分析的问题宜选用几何法。
注2：解析法（变分法）相当于“绝对法”；而几何法（运动分析法）通
常要用到“合成运动”的方法。即两种方法“对应”于运动分析的两种方 法。 12
三、虚功 力在虚位移上所做的功称为虚功。
力： W F r F r cos Xx Yy Zz 或 W mP (F ) mP (F ) 指力 F 对轴或瞬心P之矩，特别对刚体此式常用。
16
解题步骤： (一)研究整体（不取分离体），并选广义坐标； (二)（若用几何法）画出系统一组虚位移，并用广义坐标虚位 移表示所有对应主动力的虚位移； （若用解析法，不画虚位移）画出直角坐标系，并求所有对 应主动力坐标的变分； (三)列解方程。 例1：本章开头例子 如图，系统平衡。已知Q、l、 ，求P。 分析：由几何法找“运动”关系比较难，而 结构规则，故用解析法较方便。 解：选 为广义坐标，建立坐标系如图。
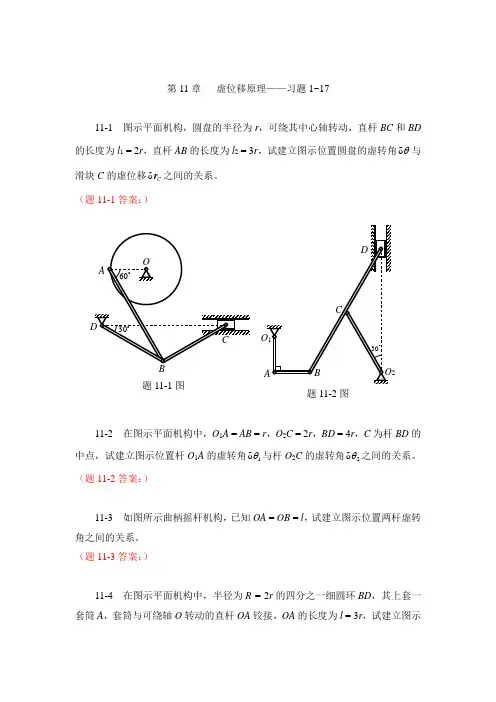
第11章 虚位移原理—习题(1~17)

第11章 虚位移原理—习题(1~17)

第11章 虚位移原理——习题1~1711-1 图示平面机构，圆盘的半径为r ，可绕其中心轴转动，直杆BC 和BD 的长度为l 1 = 2r ，直杆AB 的长度为l 2 = 3r ，试建立图示位置圆盘的虚转角θδ与滑块C 的虚位移C r δ之间的关系。

（题11-1答案：）11-2 在图示平面机构中，O 1A = AB = r ，O 2C = 2r ，BD = 4r ，C 为杆BD 的中点，试建立图示位置杆O 1A 的虚转角1δθ与杆O 2C 的虚转角2δθ之间的关系。

（题11-2答案：）11-3 如图所示曲柄摇杆机构，已知OA = OB = l ，试建立图示位置两杆虚转角之间的关系。

（题11-3答案：）11-4 在图示平面机构中，半径为R = 2r 的四分之一细圆环BD ，其上套一套筒A ，套筒与可绕轴O 转动的直杆OA 铰接，OA 的长度为l = 3r ，试建立图示题11-1图题11-2图位置杆OA 的虚转角与点D 的虚位移之间的关系。

（题11-4答案：）11-5 在如图所示平面机构中，O 1A = O 3C = O 3D = AB = l ，在图示位置，CB = O 2B =l 332，试建立该位置A 、D 两点虚位移之间的关系。

（题11-5答案：）11-6 在图示平面机构中，ABD 为边长等于a 的正三角形平板，O 1B 、O 2D 的杆长也均为a 。

机构在图示位置时，杆OE 与水平线成60◦角，A 、D 、O 2在同一水平线上，O 1B 位于铅垂位置，且OA = a ，试求此瞬时刚体O 1B 与OE 的虚转角之间的关系。

题11-3图题11-4图题11-5图题11-6图（题11-6答案：）11-7 在图示平面四连杆机构中，在杆AB 上垂直地作用有三角形分布载荷，其最大集度为q ，在杆OA 的中点作用有水平向左的主动力F ，且F = ql ，若不计各构件自重和各接触处摩擦，为使系统在图示位置平衡，所需施加的作用于杆BC 上的主动力偶矩M 的值。

理论力学：虚位移原理

理论力学：虚位移原理


y
B
内力虚功：W (Fs ) Fs
b
xE xD 2b sin 2b cos
l
A
FS D FS' E
CF
外力虚功：W (F ) FxC
xC 2l sin
xC 2l cos
x
根据虚位移原理：W 0
当0 2b
Fs
k(
0 )
b l
k ( xC
a)
当：xC a, 0
2020/12/9
变形体的虚位移原理：具有双面、理想约束处于静止的质 点系，在给定位置处于平衡的充分必要条件是，其所有外 力和内力在该位置任意给定的虚位移上所作的虚功之和等 于零。
2020/12/9
2
理论力学
§4-6 虚位移原理
例：机构如图所示，不计构件自重。 已知 AB = BC = l, 弹簧
刚度为k，当 AC = a 时，弹簧无变形。设在滑块上作用一水平
理论力学
习题：4-7、4-12、4-15
•变形体的虚位移原理
•质点系平衡的稳定性
2020/12/9
1
理论力学
§4-6 虚位移原理
三、变形体的虚位移原理
m1
F1
m2
F2
F1
m1
m2 F2
FN 1
FN 2
FN 1
FN 2
•外力(external force)：质点系外部的物体作用于质点系上的力
•内力(internal force)：质点系内部的作用力
V
nห้องสมุดไป่ตู้i1
V qi
qi
0
(*)
对于具有完整约束质点系的广义坐标的虚位移（变分）是独立的
工程力学 第23章虚位移原理习题解

工程力学 第23章虚位移原理习题解

yD = yE = l l sin θ ， δy D = δy E = cosθ δθ 2 2
习题 23-1 图
虚功式 即
− Mδθ − 2mgδy D + FδxB − Fk δxC = 0
l − Mδ θ − 2mg ( cosθ )δ θ + F (−l sin θ )δ θ − Fk (−l sin θ )δ θ = 0 2
A
δθ
δy E
D
3m 5m
F
ϕ
C
δrF δrG
ϕ
E
B
′ FN1 FN1
G
(a)
F1 δr D
F2
δr H δθ δrE δθ
ϕ ϕ
虚功式
′ δ rF sin ϕ = 0 − F1δ rD − FN 2δ rH − F2δ rE − FN2
A
5m
D
ϕ ϕ
H
FN2 ′ FN2
C
δrG
E
B
即
− F1 ⋅ 3δ θ − FN 2 ⋅ 4δθ − F2 ⋅ 2δθ − FN2 ⋅ 5δθ ⋅
y A = 5b cos
θ
2
+a
x
δϕ
b
M
C
b
5 θ δy A = − b sin δθ 2 2
θ
x B = 2b sin
θ
2
a
θ δxB = b cos δθ 2
A
mg
设丝杠的虚转角为 δ ϕ ，则
δϕ= 2π 2π b θ δ xB = cos δ θ h h 2
习题 23-2 图 (a)
y
虚功式 Mδ ϕ + mgδ y A = 0 以 δ y A ， δ ϕ 的表达式代入上式，得
第14章 虚位移原理_例题

第14章 虚位移原理_例题


弹簧原长 (600 300 )mm
弹簧后来长
(600
300 cos
)mm
弹簧缩短
(
300 cos
300 )mm
弹簧力 F
k
(
300
ቤተ መጻሕፍቲ ባይዱcos
300 )
由虚 位移原理：
M • F •ra F •rB 0 M Frr 0 0
[M
1.5(
1 cos
1)
0.3
sin cos2
0] 0
解： 对系统：建立坐标系和受力分析 解析法：
yK 6l sin yK 6l cos (1)
虚功方程：M W 6l cos 0 (2)
所以： M 6Wl cos
例6： 书14-5
当OC绕轴O摆动时，滑块A沿曲柄滑动，从而带动杆AB在导槽
内移动，不计各构 件自 重与各处摩擦。OC a，OD l
rB 2a (2)
列虚功方程：
M PrD FBxrB 0
(3)
将（1）（2）代入（3），得：
M Pa FBx 2a 0
FBx
1 M 2 a
P
（2）求B 铰的垂直约束力： 解除B 铰的垂直约束，代之以垂直力 FBy 。 杆BCD 的速度瞬心在A
rD 5a
rB 2a
M PrD
F
、F
给出力
P
、
F
处的虚位移 rD、rB
几何法： rC cos rD
C
rC cos(90 2 ) rB cos
A
θ
θ rC D F
Fθ
rB
B
由虚功原理 PrD FrB 0 0
PrC cos F 2sinrC 0 (P cos 2F sin )rC 0
《理论力学》第十三章--虚位移试题及答案

《理论力学》第十三章--虚位移试题及答案

理论力学14章作业题解思考题14-1 确定自由度。

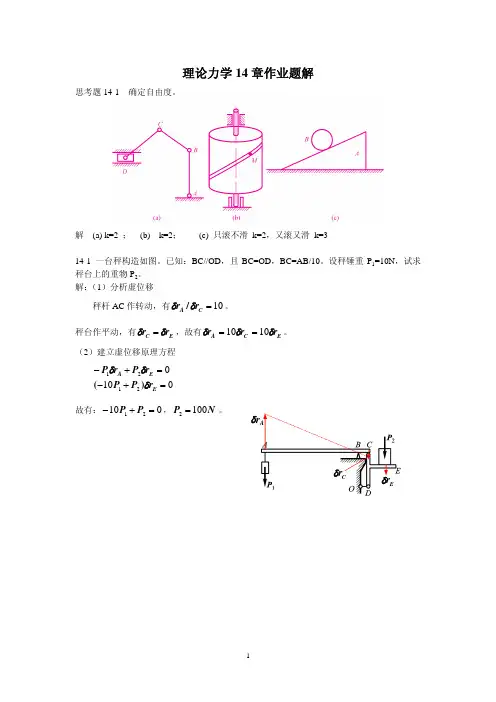
解 (a) k=2 ； (b) k=2； (c) 只滚不滑 k=2，又滚又滑 k=314-1 一台秤构造如图。

已知：BC//OD ，且BC=OD ，BC=AB/10。

设秤锤重P 1=10N ，试求秤台上的重物P 2。

解：（1）分析虚位移 秤杆AC 作转动，有10=C A r r d d /。

秤台作平动，有E C r r d d =，故有E C A r r r d d d 1010==。

（2）建立虚位移原理方程1002121=+-=+-E E A r P P r P r P d d d )(故有：01021=+-P P ，N P 1002=。

Cr d Er14-5 OA=l ，OC=R满足的条件。

解： （用虚位移原理求解）(1) 运动分析（虚位移关系分析）A 处虚位移关系用合成运动的理论分析。

A 为动点，OC 为动系。

r e A r r r r r r d d d +=f d d cos A e r r =另外：R r l r C e /d d = (2) 虚功方程fd f f d d d d cos /)cos /(cos /R l F F r R l F F R r l F r F r F r F C C C A C 21212121000==-=-=-14-9 已知：AC=BC=EC=GC=DE=DG=l ，荷载F 2。

求平衡时的F 1。

解 用解析法，1个自由度，选q 为广义坐标。

建立坐标，如图。

(1) 计算虚位移qdqd q qdq d q sin ,cos cos ,sin l y l y l x l x A A D D 2233-====(2) 计算力的投影 2211F F F F x y -=-= , (3) 建立虚位移原理方程qqdq q q d d sin cos )cos sin (230320212121F F l F l F x F y F D x A y ==×-×=+Oxy14-12 F=4kN, AO=OE=5m. 求D 解：(1) 接触D 处水平约束，代之约束力。

第十五章虚位移原理

第十五章虚位移原理

F 2l δφ
F'
B
A
W
FN s 2Fl 0


2π
s
h
h s 2π
δs FN
FN h W (2Fl 2π ) 0
FN h 2 Fl 0 2π
1 FN 4π Fl h
例题
第15章 虚位移原理
例 题 1
例题
第15章 虚位移原理
2 1 2 1
2
2 1
y
x22 y22 l32 ( x1 x2 ) ( y1 y2 ) l
2 2 2
l2 m1
m2 （x ，y ） 2 2
l3 x
l1
（x1，y1）
例3：曲柄连杆机构 约束方程为：
2 2 xA yA r2
y

r φ
A （xA，yA） l
B x （xB，yB）
xC
xC
例题
第15章 虚位移原理
例 题 7
已知图所示结构，各杆都以光滑铰链连接，且有 AC=CE=BC=CD=DG=GE=l。在点G作用一铅直方向的力F，求 支座B的水平约束反力FBx。
sin ( ) M FAr cos FB r 0 cos
例：图示平面等腰三角形机构，在C点作用主动力P,系统 处于平衡，求A、B两处的约束反力。
A、B两处共有4个反力，应逐个求之。 先求哪个反力，则解除该方向的约束，代 之以对应的反力。暂时不求的则不要解除， 仍保持原约束的性质。
力学小魔术
一根重为F的均质杆简支于A,B支座上，支座的反力 分别为F/2。如果突然将支座B撤去，显然在重力矩 作用下AB杆将绕A点顺时针转动而掉下。现在，允 许在AB杆上采取一些措施，但不能对系统施加绕A 点的外力矩，使得在支座B撤去后，AB杆仍能维持 水平而不掉下。你能做到吗？
虚位移原理例题

虚位移原理例题

虚位移原理例题虚位移原理是力学中的一个重要概念，它是描述物体在受力作用下发生位移的原理。

虚位移原理在力学、静力学、动力学等领域都有着广泛的应用。

下面我们通过一些例题来深入理解虚位移原理的应用。

例题一，弹簧振子。

一根质量为m的弹簧上挂着一个质量为M的物体，当物体受到外力F时，弹簧发生形变。

求弹簧的位移x。

解析，根据虚位移原理，我们可以假设弹簧的位移为x，那么弹簧所受的弹力为-kx，其中k为弹簧的弹簧系数。

根据牛顿第二定律，物体所受的合外力为F-kx，根据虚位移原理，这个合外力所做的虚功等于零。

因此，我们可以得到F-kx=0，解得x=F/k。

例题二，斜面上的物体。

一个质量为m的物体沿着无摩擦的斜面向下滑动，斜面的倾角为θ，斜面的高度为h。

求物体滑动的位移s。

解析，根据虚位移原理，我们可以假设物体沿着斜面滑动的位移为s，那么物体所受的重力分解成沿斜面方向的分力为mgsinθ，垂直斜面方向的分力为mgcos θ。

根据虚位移原理，物体所受的合外力为mgsinθ，这个合外力所做的虚功等于零。

因此，我们可以得到mgsinθs=0，解得s=0。

例题三，简谐振动。

一个质量为m的物体挂在一个弹簧上，弹簧的劲度系数为k。

求物体振动的最大位移A。

解析，根据虚位移原理，我们可以假设物体振动的位移为x，那么物体所受的弹力为-kx。

根据牛顿第二定律，物体所受的合外力为-mg-kx，根据虚位移原理，这个合外力所做的虚功等于零。

因此，我们可以得到-mg-kA=0，解得A=mg/k。

通过以上例题的分析，我们可以看到虚位移原理在力学问题中的重要作用。

它通过假设物体的虚位移，使得问题的分析变得简单而直观。

虚位移原理的应用不仅仅局限于上面的例题，它在静力学、动力学、弹性力学等领域都有着广泛的应用。

因此，掌握虚位移原理对于理解力学问题、解决实际问题具有重要意义。

总结：虚位移原理是力学中的一个重要概念，它描述了物体在受力作用下发生位移的原理。

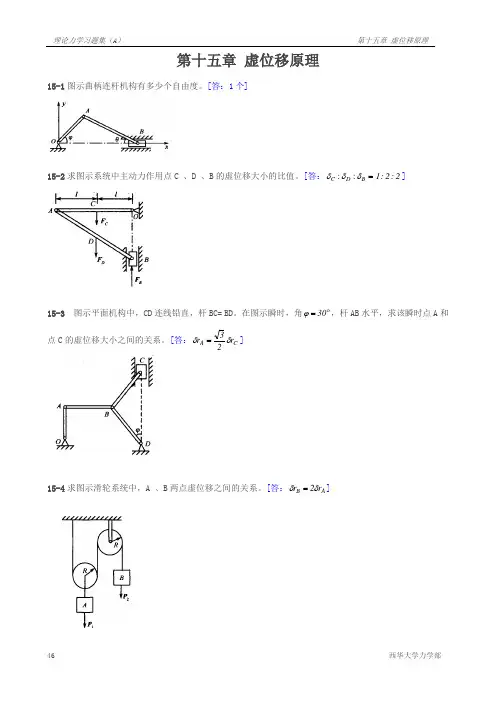
第15章 虚位移原理(古)

第15章 虚位移原理(古)

第十五章 虚位移原理15-1图示曲柄连杆机构有多少个自由度。

[答：1个]15-2求图示系统中主动力作用点C 、D 、B 的虚位移大小的比值。

[答：=B D C δδδ::2:2:1]15-3 图示平面机构中，CD 连线铅直，杆BC= BD 。

在图示瞬时，角 30=ϕ，杆AB 水平，求该瞬时点A 和点C 的虚位移大小之间的关系。

[答：C A r 23r δδ=]15-4求图示滑轮系统中，A 、B 两点虚位移之间的关系。

[答：A B r 2r δδ=]15-5重为P 、长为l 的均质杆AB 放置如图。

设各处光滑，在A 点处的水平力F 作用下保持平衡， 60=ϕ，今给A 点一向右的虚位移x δ，试由虚位移原理建立的虚功方程。

[答：0x F -63P=δδ]15-6 杆OA 和AB 各长l ，在A 点用铰链连接，在点O 和B 间连接一根刚度系数为 k 的铅直弹簧，弹簧的原长为0l 。

当在A 点作用铅垂力A F 时，机构处于图所示的平衡位置，且弹簧被拉伸。

如果不计各构件的重量和摩擦，用虚位移原理求机构处于平衡位置时的角度ϕ。

[答：4kl2kl F arcsinA +=ϕ]15-7 如图所示，两等长杆AB 和BC 在点B 用铰链连接。

在杆的点D 和点E 连接水平弹簧，弹簧的刚度系数为k ；从当距离AC a =时，弹簧的拉力等于零。

已知 AB=l , BD=b ，今在点C 作用水平力F 1使系统处于平衡。

若不计构件重量和摩擦，试用虚位移原理求距离AC 的值x 。

[答：21b l kFa x ⎪⎭⎫ ⎝⎛+=]15-8 在图示机构中，已知：力F ，l GC EG DE DC BC AC ======，弹簧的原长为l ，刚度系数为k 。

试用虚位移原理求机构平衡时，力F 与角θ的关系。

[答：()12sin kl 32F -=θ]15-9 平面机构在力F 1和F 2的作用下，在图所示的角度θ位置平衡。

已知1l BD OD ==，2l AD =，如果不计各构件重量和摩擦，试用虚位移原理求F 1 / F 2的比值。

理论力学-虚位移原理

理论力学-虚位移原理

而虚位移原理则将利用后一种情况，他通过主动力在 约束所许可的位移上的表现（通过功的形式）来给出质点 系的平衡条件。
因此，在虚位移原理中，首先要研究加在质点系上的 各种约束，以及约束所许可的位移的普遍性质。
第六章 虚位移原理
§6-2 约束和约束方程
约束与约束方程 约束的类型
第六章 虚位移原理
§6-2 约束和约束方程
式中xA，yA和xB，yB分别为A，B两点的直角坐标。上述方程表明这四 个坐标并非都独立。可以消去其中的某三个，从而只剩下一个独立坐标，
这一坐标完全确定了此质点系的位置。
以后我们改称系统的位置为位形。
第六章 虚位移原理
§6-2 约束和约束方程
约束实例
曲面
图示质点A在曲面上运动，质点A的约束方程就是曲面 的曲面方程：
z
f (x, y, z) 0
A（x, y, z)
z
y
x
x
y
第六章 虚位移原理
§6-2 约束和约束方程
约束类型
三、约束的类型
按照约束对质点系运动限制的不同情况，可将约束分类如下：
1.完整约束和非完整约束
其约束方程的一般形式为
f j (x1, y1, z1; ...; xn , yn , zn; x1, y1, z1, ...; xn, yn, zn; t) 0
约束类型
第六章 虚位移原理
非完整约束
§6-2 约束和约束方程
约束类型
2.定常约束和非定常约束
● 如果约束方程中不含时间t，这种约束称为定常约束或稳 定约束。
定常约束一般形式为
f j (x1, y1, z1; ...; xn, yn, zn; x1, y1, z1,...; xn, yn, zn;) 0
虚位移原理例题

虚位移原理例题

虚位移原理例题虚位移原理是物理学中一个非常重要的概念，它描述了光学中光线的传播规律，也是解决光学问题的基本工具之一。

下面我们通过一些例题来深入理解虚位移原理。

例题一：一根直立的圆柱形玻璃杯里装满了水，现在在玻璃杯旁边放置一个小的物体。

当我们从玻璃杯的一侧观察时，看到的物体会出现在玻璃杯的哪个位置？解析：根据虚位移原理，我们知道光线在从一种介质射向另一种介质时会发生折射。

在这个例子中，当我们从玻璃杯的一侧观察时，光线会从空气中射入水中，然后再从水中射出。

根据虚位移原理，我们可以得出结论，在观察时，物体会出现在实际物体所在位置的上方，这就是虚位移的原理。

例题二：一束光线从空气中射入玻璃中，入射角为30°，折射角为20°。

求玻璃的折射率是多少？解析：根据折射定律，我们知道入射角和折射角之间有一个固定的关系，即折射率n等于正弦入射角与正弦折射角的比值。

根据虚位移原理，我们可以通过求解这个例题来验证虚位移原理的正确性。

根据已知条件，我们可以得出：n = sin(30°) / sin(20°) ≈ 1.5。

因此，玻璃的折射率约为1.5。

例题三：一束光线从空气中射入水中，入射角为45°，求折射角和折射率是多少？解析：根据折射定律和虚位移原理，我们可以通过这个例题来进一步验证虚位移原理的正确性。

根据折射定律，我们可以得出：sin(折射角) = sin(入射角) / n。

代入已知条件，我们可以得出：sin(折射角) = sin(45°) / 1.33 ≈ 0.707 / 1.33 ≈ 0.531。

折射角约为 arcsin(0.531) ≈ 32°。

因此，光线在从空气射入水中时，折射角约为32°，折射率约为1.33。

通过以上例题的分析，我们可以更加深入地理解虚位移原理在光学中的应用。

虚位移原理是解决光学问题的重要工具，它帮助我们理解光线在不同介质中传播的规律，也为光学领域的研究提供了重要的理论基础。

理论力学(14.2)--虚位移原理


F
cotq
q q
问题：如图在 CG 间加一弹簧 , 刚度 k ,
且已有伸长量 0 , 仍求FBx .
在弹簧处也代之以力 , 如图 .
FC FG k0
δ0WF FBx �δxδBδ + FC �yC - FG �yG +F �δy0G
xB 2l cosq , yC l sinq , yG 3l sinq δx2B sin-δ, l q q cosδy,C l q3 qcos yG l qq
δδrA dt
,
vB

rB dt
￥ 代入到
Fi
�δ0ri

, 中得
为 虚速度
FBvB - FAvA 0
由速度投影定理 , 有 vB cosj vA sin j
FA FB tanj
例 14-4
已知：如图所示机构 , 不计各构件自重与各处摩擦 . 求：机构在图示位置平衡时 , 主动力偶矩Ｍ 与主动
Mw - FvC 0
M

Fh sin2 q
解析法：Mδqδ0+ F xC
xC h cotq + BC
δ xC

-
hδq sin2 q
M

Fh sin2 q
例 14-5 求图所示无重组合梁支座Ａ的约束力 .
解：解除 A 处约束，代之FA ，给虚位移，如图
δWδδFδδ0FA sA - F1 s 1+M j + F2 s2
第十四章
虚位移原 理
例 14-1
已知：如图所示 , 在螺旋压榨机的手柄 AB 上作用一在水平 面内的力偶 ( F , F), 其力矩 M ,2螺F杆l

文库最新发布：虚位移原理

8xQ = -xP
计算虚功得: W(P) = P xP
O
y
A
B
P
C
W(Q) = Q xQ
Q
由虚位移原理得: P xP + Q xQ = 0
x
代入上述变分结果得: - 8 P xQ + Q xQ = 0
Q/P = 8 21
例题7.在图示结构中,曲柄OA上作用一力偶, 其力偶矩为m,另在滑块D上作用一水平力P. 结构尺寸如图所示.求当平衡时,力P与力偶矩 m的关系.
4
(2) 解析法
先把各质点的坐标表示成广义坐标的函数,再将各式 对广义坐标求变分(与求微分相似)，得到各虚位移在相 应坐标轴上的投影。
例题.求图示机构A点和B点的虚位移.OA=AB=l ;
y
解: xA=l cos yA=l sin
xB=2l cos
yB=0 xA = -lsin
O
yA = lcos
I
解: 应用几何学和运动学来求A点
和B点的虚位移rA和 rB
2
OA杆作定轴转动
rA
2
rA = OA 1
(1)
AB杆作平面运动 , I为瞬心
A 1
rA = IA 2
(2)
O
rB
B
3
由(1)(2)式得:
I
2
=
OA IA
1
rB = IB 2
=
OA IA
IB
1
2
rA
2
A
1
O
rB
B
当然也可以取1 的转向为顺时针转向,画 出虚位移图得出的 rA和 rB的表达式与转向 为逆时针是一致的.
B是AC杆的瞬心. E是CE杆的瞬心.

第15章 虚位移原理_例题


δ y D = − 2 a sin ϕδϕ − b sinψδψ x B = 2 a sin ϕ + 2 b sinψ , δ x B = 2 a cos ϕδϕ + 2 b cosψδψ
代入(a)式，得：
( − P a sin ϕ − P2 2a sin ϕ + F 2a cos ϕ )δϕ + ( − P2b sin ψ + F 2b cosψ )δψ = 0 1
h 4、列虚功方程： δW = 2 Flδϕ − FN δs = (2 Fl − FN ) ⋅ δϕ = 0 2π
δϕ 是任意的，有： 2 Fl − h F = 0 由于 N 2π 也即：
l ∴ FN = 4π F h
讨论： 1）利用约束力不做功避免了所有约束力的出现， 这是虚位移原理解题与矢量静力学解题相比的巨大优点。 2）本题求虚位移间关系的方法为：由物理关系直接给 出法。
− M δθ − F δx B = 0
注意：几何法时，主动力与虚位移方向一致为正；
力偶、角度逆时针为正 解析法时主动力、坐标变分各自沿坐标轴方向为正，力偶、角度逆时针为正。 力偶
例4 均质杆OA及AB在A点用铰连接，并在O点用固定铰 支座，如图所示。两杆各长2a和2b，各重P1及P2，设在B点 加水平力 F 以维持平衡，求两杆与铅直线所成的角ϕ及ψ 。
而
δ rC = a δϕ , δ rB = δ rD = δ rA = 2 a δϕ
代入上式后，得：
( F cosϕ ⋅2a − P1 ⋅asinϕ − P2 ⋅2asinϕ )δϕ = 0
tgϕ =
2F P1 + 2 P2
讨论：其它可能虚位移与真实位移
例5 ：升降机构，

虚功(虚位移)原理复习与例题

由虚功方程，得
FAsA 2qlsE
M
sE
l
A
0
P
q
M
B
D
C
sC sE
其中
FA
sA sC 2sE
代入虚功方程，得
(FA
ql
M 2l
)sA
0
解得
FA
M 2l
ql
§5.2.3 用广义坐标表示的质点系平衡条件
xi xi (q1, q2 ,qs , t) yi yi (q1, q2,qs ,t)(i 1,2,, n)
虚位移与实位移的区别和联系
实位移——质点或质点系在其真实运动中，在一定的时间间 隔内发生的位移。
（1）在完整定常约束下，实位移是诸多虚位移中的一个； （2）在完整定常约束下，虚位移方向沿其速度方向。
dr ——实位移 r ——虚位移
M dre
dr
r
M1
2. 虚 功
质点或质点系所受的力在虚位移上所作的功——虚功。
自 由 度 —— 在完整约束条件下，确定质点系位置的独立参变 量的数目等于系统的自由度数。
N=3n—s
对于稳定的完整约束，各质点的坐标可以写成广义坐标的 函数形式
xi xi (q1, q2 ,qk , t) yi yi (q1, q2,qk ,t)(i 1,2,, n) zi zi (q1, q2 ,qk , t)
2l
P
q
M
BC
sE
D
sD
FD
(2) 解除B处约束，代之以反力
P
q
M
FB ，并将其视为主动力。
A
D
BC
由虚功方程，得
sB sC sE
PsB FBsB

理论力学(虚位移原理) 山东建筑大学理论力学


2
rA
C
b
rD
D
B
b
4
rB
4
I2
P
7
a
I1
O
2
A m1
利用虚位移图 2
rA
C
计算各虚位移间
rD
D
P
的关系.
b
B
b
rA =a1=I1A2 rB =I1B2 =I2B4 rB =I2D4 I1O actg2
4
rB
4
I2
I1B
a cos sin2
I2D 2bsin
sin2 cos 2
a cos b cos2
q
P2 2
W(P2) = - 1602 = - 801
P1 1 C 4
1
3
2
2
W(M) = 2002 = 1001
MA A 4
8
M
由虚位移原理得: MA1 - 301 - 601 - 801+1001= 0 rB B
MA = 70
22
q
P1 1
C r
4
P2
r
2
2
A
3
A
XA
4
r
8
M
解除A端的水平约束代之约束反力XA 画虚位移图.
例题14-19.试计算图示桁架CD杆的内力.
C A
D
B
6a
P
3a
31
解:截断CD杆代之内力SC和SD , 且SC = SD = S. 画虚位移图.B为BD部分的瞬心.亦为BH部分的瞬心. I为CI部分的瞬心.亦为DI部分的瞬心.
E为23杆的瞬心.
I
2

虚位移原理习题解答

7－1. 在图示机构中，曲柄OA 上作用一力偶，其矩为M ，另在滑块D 上作用水平力F 。

机构尺寸如图所示。

求当机构平衡时，力F 与力偶矩M 的关系。

解 设OA 杆虚位移为δϕ，则A 、B 、C 、D 各点虚位移如图，θδθδθδθδδϕδcos 2cos cos 2cos D B A B A r r r r a r ===由上述各式和虚功方程0=+-D r F M δδϕ解出θ2tan Fa M =7－2. 图示桁架中，已知AD=DB=6m ，CD=3m ，节点D 处载荷为P 。

试用虚位移原理求杆3的内力。

解 B 、C 、D 各点虚位移如图所示，θδδθδθδcos ,2sin cos C D c B r r r r ==代入虚功方程 03=-B D r F r P δδ解得杆3的内力 P PF ==θcot 23 7－3. 组合梁由铰链C 铰接AC 和CE 而成，载荷分布如图所示。

已知跨度l=8m ，P=4900N ，均布力q=2450N/m ，力偶矩M=4900N ⋅m ；求支座反力。

N 2450N 14700N 2450==-=E B A F F F ，，7－4 组合梁由水平梁AC 、CD 组成，如图所。

已知：F 1= 20kN ，F 2 = 12kN ，q = 4kN/m ，M = 2kN ·m 。

不计梁自重，试求：固定端A 和支座B 处的约束力。

组合梁由水平梁AC 、CD 组成，如图12－16a 所。

已知：F 1= 20kN ，F 2 = 12kN ，q = 4kN/m ，M = 2kN ·m 。

不计梁自重，试求：固定端A 和支座B 处的约束力。

(a)(b)2 222(d )(e)图12－16 例题12－5图解：组合梁为静定结构，其自由度为零，不可能发生虚位移。

为能应用虚位移原理确定A 、B 二处的约束力，可逐次解除一个约束，代之以作用力，使系统具有一个自由度，并解除约束处的正应力视为主动力；分析系统各主动力作用点的虚位移以及相应的虚功，应用虚位移原理建立求解约束力的方程。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例6： 书15-5
当OC绕轴O摆动时，滑块A沿曲柄滑动，从而带动杆AB在导槽
内移动，不计各构 件自 重与各处摩擦。OC a，OD l 求机构平衡时力F1与F2的关系。
解：给出力
F1
、F2
处的虚位移 rC、rA
几何法：ra rA re rr rA cos re
rC
re
a l / cos
注意：几何法时，主动力与虚位移方向一致为正；
解析法时主动力、坐标变分各自沿坐标轴方向为正，力偶、角度逆时针为正。
例4 均质杆OA及AB在A点用铰连接，并在O点用固定铰 支座，如图所示。两杆各长2a和2b，各重P1及P2，设在B点
加水平力 F 以维持平衡，求两杆与铅直线所成的角及 。
解F1
由虚功原理 F1rC F2rA 0
F1
a
F2l cos2
φD x
O
解析法：建立如图直角坐标系 yA l tan
求变分 y A
l
cos2
又rC
由虚功原理 F1rC F2yA 0
a
F1
F2l
a cos2
B
F2
例7： 书15-7
滑套D套在光滑直杆AB上，并带动杆
一组虚位移，如图所示。 图示中：
rA rD rB
FrB cos P1rC sin P2rD sin 0
而 rC a , rB rD rA 2a
代入上式后，得：
(Fcos 2aP1asin P2 2asin ) 0
tg
P1
2F 2P2
讨论：其它可能虚位移与真实位移
例5 ：升降机构，
已知： AO AB AC AD l ,
vB
2rA sin rB
解析法：
rB 2l sin
虚功方程 M FrB 0
arcsin M
2Fl
xB 2l cos xB 2l sin
( x轴向右为正，xB向右，
rB xB 2l sin)
当然，几何法
也可以假设 顺时针，
求解结果相同。
虚功方程 M FxB 0
M F 2l sin 0
(2Fl
h
2
FN )
0
由于 是任意的，有： 2Fl
也即：
h
2
FN
0
FN
4
l h
F
讨论： 1）利用约束力不做功避免了所有约束力的出现， 这是虚位移原理解题与矢量静力学解题相比的巨大优点。
2）本题求虚位移间关系的方法为：由物理关系直接给 出法。
例2 图示椭圆规机构，连杆AB长l，杆重和滑道摩擦不计， 铰链为光滑的，求在图示位置平衡时，主动力大小P和Q之间 的关系。
解：研究整个机构。 系统的所有约束都是 完整、定常、理想的。
1、几何法：使A发生虚位移 rA ，
B的虚位移 rB ，则由虚位移原理，
得虚功方程：
rA
PrA QrB 0
而 rA sin rB cos
rA
rB rA tg
(PQtg )rA 0
由rA的任意性，得 PQ tg
2、解析法 由于系统为单自由度，
由此解得：
tg
P1
2F 2P2
,
tg 2F
P2
解法二： 应用虚位移原理，几何法
先使 保持不变，而使 获得变分 ，得到系统的一
组虚位移，如图所示。
FrB cos P2rD sin 0
而 rB 2b , rD b
代入上式，得
tg
F 2b P2 b
2F P2
再使 保持不变，而使 获得变分 ，得到系统的另
CD在铅直滑道上滑动。已知=0o时，
弹簧等于原长，弹簧刚度系数为
5(kN/m)，求在任意位置（ 角）平衡
时，加在AB杆上的力偶矩M ？
解：这是一个已知系统平衡，求作用于系统上主动力之间关系 的问题。将弹簧力计入主动力，系统简化为理想约束系统，故 可以用虚位移原理求解。
选择AB杆、CD杆和滑套D的系统为研究对象。
统，取角及为广义坐标，现用两
种方法求解。 y
解法一： 应用虚位移原理，解析法
P1yC P2yD FxB 0 (a) 而 yC acos , yC asin
yD 2acos bcos , yD 2asin bsin xB 2asin 2bsin , xB 2acos 2bcos
代入(a)式，得：
K
CE DE FE EG FH l , HG IH HJ l ,
机构的平衡位置为 ，
试求力偶M与重物 W 间的关系。
解： 对系统：建立坐标系和受力分析 解析法：
yK 6l sin yK 6l cos (1)
虚功方程：M W 6l cos 0 (2)
所以： M 6Wl cos
re
300
cos
rr
re
tan
300sin cos2
去掉弹簧，暴露出弹簧力 F和
F
ra re
rB F rr
F
弹簧原长 (600 300 )mm
弹簧后来长
(600
300 cos
)mm
弹簧缩短
(
300 cos
300 )mm
例1：螺旋压榨机中螺杆的螺距为 h 。如果
在手柄上作用一在水平面内的力偶，其
力偶矩为 2Fl ，求平衡时作用于被压榨
物体上的压力。（忽略摩擦）
解：
1、对象：由手柄、螺杆及压板组成的系统
23、、分给析系受统力以：虚主位动移力：（F和, F’s有 )及，：压s板阻h力FN
2
4、列虚功方程：W
2Fl
FNs
(P1a sin P2 2a sin F 2a cos) (P2bsin F 2b cos ) 0
(P1asin P2 2asin F2a cos) (P2bsin F2bcos ) 0 由于 , 是彼此独立的，所以：
P1asin P2 2asin F2acos 0 P2 bsin F2bcos 0
机构。今在OA杆上作用力偶 M ，在滑块B上作用力 F ，使 机构处于平衡状态，如例图所示。试求平衡位置角 。 解：1、对象：系统
2、分析受力：M，F
3、给虚位移： ， rB ，求虚位移关系：
几何法(虚位移投影法或者瞬心法)：
rA l
OA vA
rA cos(90 ) rA sin 2 rB cos
可取为广义坐标。
xB lcos , yA lsin xB lsin , yA lcos
Py A QxB 0 ,
(Pcos Qsin )l 0
由于 任意，故 PQ tg
注意：几何法时，主动力与虚位移方向一致为正； 解析法时主动力、坐标变分各自沿坐标轴方向为正
OA vA vB
例3：两均质杆 OA AB l ，均不计重，构成曲柄滑块