虚功原理应用例题

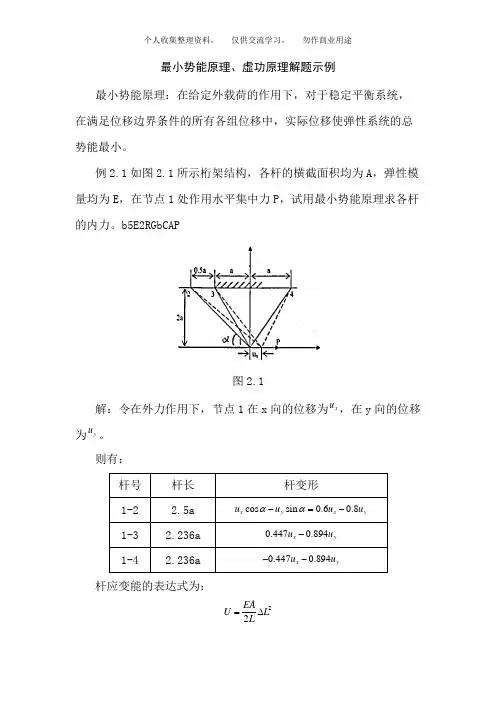
9 虚功原理和结构的位移计算习题1. 引言虚功原理是结构力学中一项重要的基本原理，它可以用于解决各种结构的位移计算问题。

本文将通过一些习题来演示如何应用虚功原理进行位移计算。

2. 虚功原理简介虚功原理是指在结构力学中，结构在虚位移下所进行的虚功等于零。

虚位移是指结构在受力作用下的无限小位移，不违反实际情况下的几何和边界条件。

利用虚功原理，可以建立结构的平衡方程，并求解未知的位移。

3. 习题一考虑一个简支梁，受到一个集中力F作用在梁的中点。

已知梁的长度L和截面的惯性矩I，求梁的最大挠度。

解答：根据虚功原理，可以得到以下方程：$$\\int_{0}^{L} M \\cdot \\delta dL - F \\cdot \\delta\\cdot \\frac{L}{2} = 0$$其中M为弯矩，$\\delta$为虚位移。

由弯矩与挠度之间的关系，可以得到：$$M = -\\frac{F}{2}L + F \\cdot x$$代入上述方程，得到：$$\\int_{0}^{L} \\left(-\\frac{F}{2}L + F \\cdot x\\right) \\cdot \\delta dL - F \\cdot \\delta \\cdot \\frac{L}{2} = 0$$对上述方程两边进行积分并整理，可以得到：$$\\frac{FL^3}{6EI} = \\delta$$所以梁的最大挠度为$\\frac{FL^3}{6EI}$。

4. 习题二考虑一个简支梁，长度为L，弹性模量为E，截面惯性矩为I，受到一个均布载荷q作用在梁上。

已知梁的两端处的位移分别为0和$\\delta_1$，求梁上某一点的位移。

解答：根据虚功原理，可以得到以下方程：$$\\int_{0}^{L} \\left(-M\\right) \\cdot \\delta dL -\\int_{0}^{L} q \\cdot \\delta dL = 0$$对上述方程两边进行积分并代入弯矩与挠度之间的关系，可以得到：$$\\frac{1}{2}EI \\cdot \\delta - \\frac{qL^2}{2} \\cdot \\delta = 0$$整理上述方程，可以求解出$\\delta$的值。

虚功原理(物理竞赛)§2、虚功原理上次课主要是介绍了分析力学中经常要用到的一些基本概念，并由虚功的概念和理想约束的概念导出了解决静力学问题的虚功原理：0=⋅∑i r i F δ。

虚功原理适用的范围是：质点组，它适用的前提条件是只受理想约束。

这次课就举一些具体例子，使我们能够了解如何利用虚功原理去解决静力学问题。

三、应用虚功原理解题：例1、如图所示，有一质量为m ，长度为 的刚性杆子，靠在墙上，在与地面接触的B 端上受一水平向左的外力F ，杆子两端的接触都是光滑的，当杆子与水平地面成α角时，要使杆子处于平衡状态，问作用在杆子B 端上的力F 有多大？求F =？解：由题意可知它是一个静力学问题，而且接触都是光滑的，显然可以应用虚功原理来求解这个问题。

这个例子很简单，简单的题目往往能够清楚地说明物理意义，为了说明虚功原理的意义，如果一开始就举复杂的例子，由于复杂的数字计算将会掩盖物理意义，所以就以这个简单的例子来看看如何应用虚功原理来解出它。

第一步当然也是确定研究对象，即①选系统：在这个例题中，我们就取杆子为应用虚功原理的力学系统。

②找主动力：作用在我们所选取的系统上的主动力有几个？有两个。

一个是水平作用力F ，还有一个是重力m g 作用在杆子的质心上。

因为杆子两端A 、B 处的接触是光滑的，∴在该两处的约束力也就不必考虑。

③列出虚功方程：主动力找出来以后，视计算方便起见，适当选好坐标，并根据虚功原理列出虚功方程。

现在选取如图所示的直角坐标，于是我们现在就可列出系统的虚功方程。

列虚功方程时，正、负号是个很重要的问题，如果按虚位移的实际方向与力的方向间的关系确定虚功的正负号，很容易弄错。

为了不容易弄错，我们还是按力的作用点的坐标的正方向与力的方向间的关系来确定虚功的正负号。

这种方法既方便而又不容易搞错。

在列方程时必须要注意这个问题。

∵F 的方向与其作用点的坐标X 的正方向相反，∴F 取负而δX B 取正，∴此力的虚功为负的，即：0=--C B y mg x F δδ……①，由于虚功方程中的两个虚位移不是相互独立的，∴我们还需要将它们化成独立变量，然后才能令独立虚位移前的乘数等于零，从而求出最后的结果。

§2、虚功原理上次课主要是介绍了分析力学中经常要用到的一些基本概念，并由虚功的概念和理想约束的概念导出了解决静力学问题的虚功原理：0=⋅∑i r i F δ。

虚功原理适用的范围是：质点组，它适用的前提条件是只受理想约束。

这次课就举一些具体例子，使我们能够了解如何利用虚功原理去解决静力学问题。

三、应用虚功原理解题：例1、如图所示，有一质量为m ，长度为 的刚性杆子，靠在墙上，在与地面接触的B 端上受一水平向左的外力F ，杆子两端的接触都是光滑的，当杆子与水平地面成α角时，要使杆子处于平衡状态，问作用在杆子B 端上的力F 有多大？求F =？解：由题意可知它是一个静力学问题，而且接触都是光滑的，显然可以应用虚功原理来求解这个问题。

这个例子很简单，简单的题目往往能够清楚地说明物理意义，为了说明虚功原理的意义，如果一开始就举复杂的例子，由于复杂的数字计算将会掩盖物理意义，所以就以这个简单的例子来看看如何应用虚功原理来解出它。

第一步当然也是确定研究对象，即①选系统：在这个例题中，我们就取杆子为应用虚功原理的力学系统。

②找主动力：作用在我们所选取的系统上的主动力有几个？有两个。

一个是水平作用力F ，还有一个是重力m g 作用在杆子的质心上。

因为杆子两端A 、B 处的接触是光滑的，∴在该两处的约束力也就不必考虑。

③列出虚功方程：主动力找出来以后，视计算方便起见，适当选好坐标，并根据虚功原理列出虚功方程。

现在选取如图所示的直角坐标，于是我们现在就可列出系统的虚功方程。

列虚功方程时，正、负号是个很重要的问题，如果按虚位移的实际方向与力的方向间的关系确定虚功的正负号，很容易弄错。

为了不容易弄错，我们还是按力的作用点的坐标的正方向与力的方向间的关系来确定虚功的正负号。

这种方法既方便而又不容易搞错。

在列方程时必须要注意这个问题。

∵F 的方向与其作用点的坐标X 的正方向相反，∴F 取负而δX B 取正，∴此力的虚功为负的，即：0=--C B y mg x F δδ……①，由于虚功方程中的两个虚位移不是相互独立的，∴我们还需要将它们化成独立变量，然后才能令独立虚位移前的乘数等于零，从而求出最后的结果。

虚功原理的应用例题背景介绍虚功原理是运用能量守恒定律和位移无关性原理进行分析和计算的一种力学方法。

它常用于解决复杂的力学问题，特别是在涉及非保守力、摩擦力和弹性力等情况下。

本文将通过一个应用例题来说明虚功原理的具体应用方法。

例题描述一个质量为m的物体沿着斜面下滑，斜面的倾角为θ。

物体在滑动过程中受到了摩擦力的作用，摩擦力的大小与物体所受重力的垂直分量相等，滑动过程中物体从斜面顶端下滑到斜面底端的高度为h。

求解物体从斜面顶端到斜面底端所做的总功。

解题思路1.分析力的情况：由题目可知，物体在下滑过程中受到重力和摩擦力的作用。

重力的大小为mg，沿斜面方向的分量为mg sinθ，垂直斜面方向的分量为mg cosθ。

摩擦力的大小与物体所受重力的垂直分量相等，即摩擦力的大小为mg*cosθ。

2.确定参考系：我们选择将斜面的下方为参考系原点，沿斜面向下为正方向。

3.确定位移情况：物体从斜面顶端下滑到斜面底端的位移为h，我们将其定义为正方向的位移。

4.应用虚功原理：根据虚功原理，物体从斜面顶端到斜面底端所做的总功等于物体受到的净外力在位移方向上的虚功之和。

在本例中，物体受到的净外力为mg sinθ-mg cosθ，位移方向为正方向，因此总功等于净外力在位移方向上的虚功。

5.计算虚功：净外力在位移方向上的虚功等于力的大小乘以位移的大小。

净外力为mg sinθ-mg cosθ，位移的大小为h。

因此，总功等于( mg sinθ-mg cosθ)*h。

结论物体从斜面顶端到斜面底端所做的总功为( mg sinθ-mg cosθ)*h。

总结本文通过一个应用例题，介绍了虚功原理的应用方法。

在解决问题时，我们需要分析力的情况，选择合适的参考系，确定位移方向，并应用虚功原理进行计算。

虚功原理在解决非保守力、摩擦力和弹性力等复杂力学问题时具有重要的应用价值。

通过学习和掌握虚功原理的应用方法，我们能够更好地理解力学问题并解决实际问题。

§2、虚功原理上次课主要是介绍了分析力学中经常要用到的一些基本概念，并由虚功的概念和理想约束的概念导出了解决静力学问题的虚功原理：0=⋅∑i r i F δ。

虚功原理适用的范围是：质点组，它适用的前提条件是只受理想约束。

这次课就举一些具体例子，使我们能够了解如何利用虚功原理去解决静力学问题。

三、应用虚功原理解题：例1、如图所示，有一质量为m ，长度为 的刚性杆子，靠在墙上，在与地面接触的B 端上受一水平向左的外力F ，杆子两端的接触都是光滑的，当杆子与水平地面成α角时，要使杆子处于平衡状态，问作用在杆子B 端上的力F有多大？求F =？解：由题意可知它是一个静力学问题，而且接触都是光滑的，显然可以应用虚功原理来求解这个问题。

这个例子很简单，简单的题目往往能够清楚地说明物理意义，为了说明虚功原理的意义，如果一开始就举复杂的例子，由于复杂的数字计算将会掩盖物理意义，所以就以这个简单的例子来看看如何应用虚功原理来解出它。

第一步当然也是确定研究对象，即①选系统：在这个例题中，我们就取杆子为应用虚功原理的力学系统。

②找主动力：作用在我们所选取的系统上的主动力有几个？有两个。

一个是水平作用力F ，还有一个是重力m g 作用在杆子的质心上。

因为杆子两端A 、B 处的接触是光滑的，∴在该两处的约束力也就不必考虑。

③列出虚功方程：主动力找出来以后，视计算方便起见，适当选好坐标，并根据虚功原理列出虚功方程。

现在选取如图所示的直角坐标，于是我们现在就可列出系统的虚功方程。

列虚功方程时，正、负号是个很重要的问题，如果按虚位移的实际方向与力的方向间的关系确定虚功的正负号，很容易弄错。

为了不容易弄错，我们还是按力的作用点的坐标的正方向与力的方向间的关系来确定虚功的正负号。

这种方法既方便而又不容易搞错。

在列方程时必须要注意这个问题。

∵F 的方向与其作用点的坐标X 的正方向相反，∴F 取负而δX B取正，∴此力的虚功为负的，即：0=--C B y mg x F δδ……①，由于虚功方程中的两个虚位移不是相互独立的，∴我们还需要将它们化成独立变量，然后才能令独立虚位移前的乘数等于零，从而求出最后的结果。

匀质杆AB始终在平面内，A端靠在墙上，B端在一光滑曲面上，如图所示。

若无论B在何处杆均受力平衡，求曲面方程。

如图所示，四根相同的长度为l的光滑轻杆由铰链连接成菱形，一轻绳系在两对角线之间，下部挂一重量为P的重物，系统放置于两根等高相距为2a（2a<2l）的杆上，求绳中的张力？（φ角已知）如图所示，一竖立在竖直平面内的半圆空心管，管内刚好装有2n个光滑小珠子，已知每个珠子重力为W，求第i个珠子与第i+1个珠子的作用力Ni。

如图所示，一个外半径为R1，内半径为R2的圆柱形电容器，竖直地插进相对介电常数为εr 的密度为ρ的电解液中，若将电容器接上电压为U 的电源，求电解液中液面上升的高度第一题，常规做法用受力分析，建立水平竖直方向平衡方程，暴力解之。

（约束力合力沿法向）能量方法，利用随遇平衡，势能V 恒不变，解得y=f(x)。

（具体见高妙）虚功原理：因为此题为理想约束，主动力为重力，虚位移中主动力做功为0，即 P δyc=0 yc=常量由几何关系：yc=y+2221x l - 故yc=y+2221x l -=常量 因x=0时y=0，故常量=21故y=21⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--2x 11l第二题，直接虚功原理……建立如图所示坐标系，把绳子忽略，于是两个拉力变为主动力T ，另一个主动力为P ，约束为理想约束，则有：x A =lsin ϕ ϕδϕδcos x l A =………………………………………..①ϕδϕϕδϕϕδϕ2sin sin 2cot cos 2al y a l y P P +-=-=……………….②由虚功原理得：-2T P A P y x δδ+=0 将①②代入，得T=P ⎪⎪⎭⎫⎝⎛-ϕϕϕtan cos sin 22l a第三题设任意珠子的球心到管的圆心为OO ’长度为R ，前面i 个球为系统质心为C ，设CO 长度为L 。

由虚功原理：N ()θθθθαd Wd L iWd d R cos i sin cos i == 其中α=n4π即N αθcos cos i R iWL =现在的目的就是求质心的位置函数L 和θ 由对称性已知角度θ=ααi i =221求L 用旋转矢量，如图所示I 个大小为mR 、方向一次相差角度2α的矢量和的大小应该为imL 有：()()ααααsin sin sin sin 22imL i i R L i mR ==即代入N 的表达式得：()()()()W n n i i i W R i i i P iWR iWL N i ⎪⎪⎪⎪⎭⎫ ⎝⎛====2sin 2sin cos sin cos sin cos cos sin sin cos cos ππαααααααααθ第四题为了求液面上升高度，就得求液体所受电场力。

虚功原理解题步骤分析约束,确定自由度选好广义坐标写出主动力作用点的坐标并对其变分代入虚功原理公式中求解Attention:静系中的平衡只有广义坐标方可独立变化虚功原理中不出现约束力)(t q r r rr =正确写出原理求棒全长。

yxmgα分析自由度数目1xmgBDαsin )(l C −=αc 0]sin 2cos )2cos 2[(2=−−δααααa l a mg]sin 2cos )2cos 2[(2−−δααααa l a mg !!!0≠δαQ ααcos )1cos 2(42−=∴a l αcos 2a ca c l )2(422−=∴0=αsin )(AC AD y c −=ααsin )2cos 2(l a −=∂∂αcr r r ααq r F Q i ii ∂∂•=∑r r 2l 0]sin 2cos )2cos 2[(=−−αααa l a mgrABFr y分析自由度2广义坐标βα,βDdemonstrationgm r gm rαsin 2l y =βαsin 2sin l l y +=2l 2l BD C x F y mg y mg w δδδδ++=)sin (sin βδβαδα+−l2l δ2l l y =)βδβδβββδαα)sin cos 2()sin 23Fl mg l l −+0=δβββ)sin cos (23Fl mg l l −0=!!!0≠可任意变化且和δβδαQ 23αl 0)sin cos 2(=−ββFl mg l23l 2−l F mg 23αF2c Q =j mg Fd i F F B =l j lα2sin 2+l l i l r r 2sin ()cos 2αβ++ααq r F Q iii ∂∂•=∑r r ααα∂•+∂•+∂•=B B D D c c F F F r r r 0sin cos 23=−=ααFl mgll j lα2sin 2+j l l i l l r r r r sin 2sin ()cos 2cos (αβα+++=i l l r r r)cos cos (βα++=βββ∂+∂+∂Bd c F mg δββ2l 0=Fmg tg 2=β试用虚功原理求平衡菱形的顶角为2α,一重为W的重物,C点系yTr分析自由度广义坐标α?!!!解除一个约束一个自由度Wααactg l yc −=cos 2αc D =0=0]cos =δαα0≠可任意变化且δαQ )csc sin 2(cos 22αααa l l w T −=yxθ),(y x B ),(c c y x c 定曲面上,如果杆在与竖直墙间的夹角< 的任意位置均能平衡,试求曲面形状.2π2l δ2l y −=???=δθθδd dy y =))((θx y y =c 2(−θld 0≠δθQ 2−∴θld dy 02=−∴θl d dx dx θsin l x =Qθd dx ∴2−∴θl d dx dx θd dx2222x l x l tg l dx −==θx l −22212l 22212xl l y −−=1)2()2(2222=−+l l y l xMrr ABCl l 43ll 411x 2x 3x 取广义坐标为)(33211x x x q ++=)(21312x x q −=)2(313213x x x q +−=求相应广义力???===Q Q Q '3F r r 2F lM F l M F FF F F r r r r rr r r −===='33214143)2('x F x F x F x F W δδδδδr r r r Q +++=)(1x x x q ++=321121q q q x δδδδ++=312q q x δδδ−=321321q q q x δδδδ+−=)3()2381()43(321q l M F q lM F q F W δδδδ++−+=Q MF Q F Q 3−==。

虚功原理例题虚功原理是力学中的一个重要原理，它是用来分析静力学和动力学问题的有效方法。

虚功原理的应用范围非常广泛，可以用来求解各种复杂的结构和力学问题。

下面，我们通过一些例题来深入理解虚功原理的应用。

例题一，弹簧力的虚功。

假设有一个弹簧，其劲度系数为k，原长为l0。

现有一个质量为m的物体，静止放在弹簧的一端，另一端固定在墙上。

现在用一个外力F缓慢地将物体拉伸至位移x处，然后保持静止。

求弹簧的变形量和外力F。

解，根据虚功原理，外力F对物体所做的虚功等于弹簧对物体所做的虚功。

因为在静止状态下物体受到的合外力为零，所以外力F和弹簧的弹力大小相等，方向相反。

虚功原理可以表示为Fδx = kxδx，即Fdx = kxdx，两边积分得到∫Fdx = ∫kxdx，解得F = kx。

例题二，斜面上的物体。

有一质量为m的物体放在倾角为α的光滑斜面上，斜面的长度为L。

现在用一个外力F水平地拉动物体，使其在斜面上运动，求外力F。

解，根据虚功原理，外力F对物体所做的虚功等于重力对物体所做的虚功。

在斜面上，物体受到的重力分解为垂直于斜面方向和平行于斜面方向的两个分力，其中平行于斜面方向的分力不做虚功。

所以外力F对物体所做的虚功等于重力在斜面方向上的分力mgsinα与位移L的乘积，即Fδx = mgsinαδx，解得F = mgsin α。

例题三，摩擦力的虚功。

有一质量为m的物体放在水平面上，施加一个外力F使其运动，求外力F。

解，根据虚功原理，外力F对物体所做的虚功等于摩擦力对物体所做的虚功。

摩擦力的大小与物体所受的压力成正比，所以外力F对物体所做的虚功等于摩擦力f与位移x的乘积，即Fδx = fδx，解得F = f。

通过以上例题的分析，我们可以看到虚功原理在力学问题中的重要应用。

它可以帮助我们求解各种复杂的力学问题，是力学分析中的重要工具。

希望通过这些例题的学习，能够对虚功原理有更深入的理解，为进一步学习力学打下坚实的基础。

虚功原理例题虚功原理是力学中的一个重要原理，它在解决静力学和动力学问题中有着广泛的应用。

虚功原理的核心思想是系统受力平衡时，任何虚位移所做的功都为零。

通过虚功原理，我们可以简化和系统化力学问题的求解过程，使得复杂的力学问题变得更加清晰和易于理解。

下面，我们通过几个例题来深入理解虚功原理的应用。

例题一：如图所示，质量为m的物体通过绳子和光滑的滑轮与墙面连接，滑轮的质量可以忽略不计。

求当物体下降h时，绳子所做的功。

解析：根据虚功原理，我们可以假设物体下降了Δh的虚位移，此时绳子所做的虚功可以表示为W=mgΔh。

由于绳子是光滑的，所以滑轮对绳子所做的虚功为零。

根据虚功原理，物体所受的重力和绳子的拉力平衡，因此绳子所做的虚功也为零。

所以绳子所做的功为零。

例题二：一个质量为m的物体放在倾角为θ的光滑斜面上，斜面的长度为L。

求当物体下降h时，重力对斜面所做的功。

解析：当物体下降h时，我们可以假设斜面上升Δh的虚位移，此时重力对斜面所做的虚功可以表示为W=mgΔh。

根据虚功原理，斜面对物体的支持力与物体下降的高度有关，所以斜面对物体所做的虚功也不为零。

根据几何关系，斜面对物体所做的功可以表示为W=mgLsinθ。

因此，重力对斜面所做的功为W=mgLsinθ。

例题三：一个质量为m的物体通过绳子与墙面连接，绳子的另一端连接着一个质量为M的物体。

求当物体下降h时，绳子对墙面的拉力所做的功。

解析：当物体下降h时，我们可以假设绳子下降Δh的虚位移，此时绳子对墙面的拉力所做的虚功可以表示为W=TΔh。

根据虚功原理，绳子对墙面的拉力与物体下降的高度有关，所以绳子对墙面的拉力所做的虚功不为零。

因此，绳子对墙面的拉力所做的功为W=Th。

通过以上例题的分析，我们可以看到虚功原理在力学问题中的重要作用。

它不仅可以简化问题的求解过程，还可以帮助我们更加深入地理解力学问题背后的物理本质。

希望通过这些例题的讲解，能够对虚功原理有一个更加清晰的认识。

举例虚功原理的应用1. 背景虚功原理是力学中的一个基本原理，它在各个领域都有广泛的应用。

本文将以实例的形式说明虚功原理在实际工程中的应用。

2. 实例一：汽车刹车系统汽车刹车系统是利用摩擦产生的阻力来减慢或停止车辆运动的装置。

在刹车系统中，虚功原理被广泛应用。

•刹车系统由刹车片和刹车盘组成，当踩下刹车踏板时，刹车片与刹车盘之间会产生摩擦力。

•虚功原理指出，摩擦力所做的功等于阻止车辆运动的虚功。

•通过计算摩擦力的大小和移动距离，可以得出虚功大小，从而判断刹车系统的性能是否良好。

3. 实例二：液压缸的工作原理液压缸是一种利用液体压力来产生线性运动的装置，在工业自动化领域广泛应用。

虚功原理在液压缸的工作中发挥了重要作用。

•液压缸中通过控制液体的流动和压力，可以产生力和运动。

•当液压缸推动一个物体或执行某项工作时，液压缸所做的功等于虚功。

•通过计算液压缸所做的功，可以优化液压缸的设计和效率。

4. 实例三：电磁感应原理电磁感应是物理学中的一个重要概念，也是现代电子技术的基础。

在电磁感应中，虚功原理被广泛应用。

•当导体中的磁通量发生变化时，会在导体中产生感应电动势。

•根据虚功原理，感应电动势的大小等于感应电流通过闭合回路所做的虚功。

•通过分析感应电动势的大小和方向，可以推导出电磁感应的原理，并应用于电动机、发电机等设备的设计和优化。

5. 实例四：水力发电站水力发电是一种利用水流驱动涡轮发电的方法。

在水力发电站中，虚功原理被用于优化能量转换和提高发电效率。

•水力发电站将水流引导到涡轮上，涡轮叶片受到水流的冲击而转动。

•虚功原理指出，水流对涡轮叶片所做的功等于涡轮对水流所做的虚功。

•通过分析涡轮和水流之间的虚功关系，可以确定涡轮的设计参数和水流的引导方式，以提高发电效率。

6. 总结虚功原理是一种广泛应用于工程领域的物理原理。

本文介绍了汽车刹车系统、液压缸、电磁感应和水力发电站等实例，说明了虚功原理在这些实际工程中的应用。

最小势能原理、虚功原理解题示例最小势能原理：在给定外载荷的作用下，对于稳定平衡系统，在满足位移边界条件的所有各组位移中，实际位移使弹性系统的总势能最小。

例2.1如图2.1所示桁架结构，各杆的横截面积均为A,弹性模量均为E,在节点1处作用水平集中力P,试用最小势能原理求各杆的内力。

b5E2RGbCAP解：令在外力作用下，节点1在x向的位移为"丫，在y向的位移为叭。

则有:杆应变能的表达式为:2L则系统的总势能为:Yl = ^U-Pu x= EA(0.6n v— 0.8z< f + ———(0.447M V- 0.894"、.)2x2.5小” 〉丿2x2.236c八x y)+ ———(-0・447攸-0.894"、)' - Pit2x2・236a、x x号(0.16 吩0.192 吧+ 0.486讣他由最小势能原理可知，当结构处于稳定平衡状态时，有:BP：£4一(0.323你一0.192仏)—P = 0一(―0.192/+0.972叭)=0解得:3.51%U = --------A EA0.694%Wy= EAN— = 0.62PN-3 = 0.425PN— = -0.979P例2. 2如图2. 2所示的梁，其上作用有均布载荷q,试用最小势能原理求其挠度曲线。

ano；on 比杆的内力可由公式: 求得，故各杆的内力为:图2.2解：令梁的挠度函数为巩X）,它必须满足以下几个条件：1、必须满足几何边界条件，但不一定满足平衡条件和力的边界条件；2、由于有均布载荷q的作用，故巩“）应为x的4次多项式。

故，考虑到梁左侧为固支，可设：0(x) = X? (。

0 — qx—a2x2)梁右侧需满足:飒叽产°且梁右侧没承受弯矩，有：d~co（x\ 加=°z 〈力的边界条件）代入边界条件，有：y Y飒厶）=q厶0.6x2 - — + 0.4 —< L L丿U=[L\EJ\^\ dx等截面梁的弯曲应变能表达式为：2 <dx~丿【根据平面假设，梁在受弯曲变形后，其横截面仍保持为平面, 它一方面有挠度飒X）, —方面横截面在梁变形过程中旋转了一个角dco度石,由于该转角的存在，使得距离中性轴为y处的x方向的位移dco d 2co ^d 2cou = —y --- e = — V --- (T = — v/s --为 • dx ,应变”• dF ,弯曲应力为xdj 因此，等截面梁的弯曲应变能为:plEanqFDPw则系统的总势能为:(o 23、3x x8co{x) = L 1.2兀一 一+ 1.6 —< L U 丿由于变分可取任意值，故有:9.6 E/q = qL=叮爲所以:叩挣gj 閔亦丿G 叫7心加乂n=Ld 2a )(x) dx 2q^x)a )^x)dx由最小势能原理可知, 当结构处于稳定平衡状态时，有:又:d?Q (x)dx 2=j ： EJ" ：[')5e(jr)dx-j ：q(x)5Q (x)dx = \L EJ ^ Jo L =0&?(x) dx- J*。