理论力学虚功原理

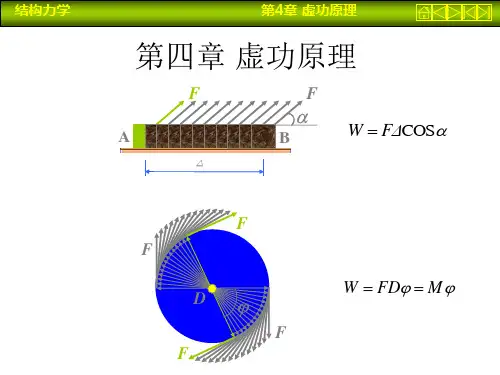
什么是理论力学中的虚功原理？在理论力学的广袤天地中，虚功原理犹如一颗璀璨的明珠，闪耀着智慧的光芒。

它是解决力学问题的重要工具，为我们理解物体的运动和受力情况提供了独特的视角。

那么，究竟什么是理论力学中的虚功原理呢？让我们一同踏上探索之旅。

要理解虚功原理，首先得明白“功”这个概念。

在物理学中，功等于力与在力的方向上移动的距离的乘积。

当一个力作用在物体上，并且物体在这个力的方向上发生了位移，我们就说这个力做了功。

而虚功原理所涉及的“虚功”，并非我们通常意义上实实在在的功。

它是一种假想的、假设的功。

想象一下，在一个力学系统中，我们假设物体发生了一个微小的、符合约束条件的位移，而在这个假设的位移过程中，所有的力所做的功之和就是虚功。

虚功原理的核心表述是：在一个处于平衡状态的理想完整约束系统中，所有主动力在任何虚位移上所做的虚功之和等于零。

为了更深入地理解这个原理，我们来举个简单的例子。

假设有一个静止在水平面上的滑块，受到水平方向的力F 和竖直方向的支持力N 。

滑块被限制在水平方向上移动，这就是一种约束条件。

现在假设滑块发生了一个微小的水平位移δx ，在这个虚位移中，支持力 N 因为垂直于位移方向，所以做功为零。

而主动力 F 所做的虚功为F·δx 。

由于滑块处于平衡状态，根据虚功原理，F·δx ＝0 ，这也就意味着力F 为零。

再来看一个稍微复杂点的例子——一个简单的杠杆系统。

杠杆的一端施加一个力F1 ，另一端施加一个力F2 ，杠杆围绕一个固定点转动。

假设杠杆发生了一个微小的转动角度δθ ，在这个虚位移中，力 F1 和F2 所做的虚功分别为F1·r1·δθ 和F2·r2·δθ （其中 r1 和 r2 分别是力 F1和F2 作用点到支点的距离）。

因为杠杆处于平衡状态，根据虚功原理，F1·r1·δθ F2·r2·δθ ＝ 0 ，从而可以得出我们熟悉的杠杆平衡条件 F1·r1＝ F2·r2 。

虚力原理和虚功原理的应用一、虚力原理的应用虚力原理是力学中常用的解题方法之一，它通过构造一个等效的问题，将原问题简化为一个虚问题来求解。

下面是虚力原理在实际问题中的应用：1.平衡力的分析：在静力学中，虚力原理常用于平衡力的分析。

例如，当一个物体处于平衡状态时，可以通过设定一个合适的虚拟力来分析平衡的条件。

虚拟力可以使原问题中的力的合力为零，从而简化问题的分析。

2.静力平衡问题：虚力原理可以应用在静力平衡问题的求解中。

对于一个静力平衡的物体，可以通过虚力原理构造一个平衡方程，解出物体所受力的大小和方向。

3.倾斜平面问题：对于一个倾斜平面上的物体，可以利用虚力原理推导出物体所受的支持力和摩擦力的大小和方向。

通过分析虚力和实际力之间的关系，可以简化问题的求解过程。

4.力的分解：虚力原理还可以应用于力的分解问题。

当一个力可以分解为若干个虚力的合力时，可以利用虚力原理将原力分解为虚力，从而简化力的分析和计算。

二、虚功原理的应用虚功原理是力学中的另一个重要原理，它通过构造一个虚位移，研究力所作的虚功来求解力学系统中的问题。

以下是虚功原理在实际问题中的应用：1.弹簧力的分析：虚功原理常用于求解弹簧力的大小和方向。

通过设定一个虚位移，并计算力所作的虚功，可以得到弹簧力与位移的关系。

这对于弹簧系统的分析和设计非常重要。

2.浮力的计算：虚功原理可以应用于计算浮力。

当一个物体部分浸没在液体中时，可以通过设定一个虚位移，计算浮力所作的虚功来求解浮力的大小。

虚功原理为浮力的计算提供了一个简洁而有效的方法。

3.压力的分析：虚功原理可以应用于分析液体或气体中的压力。

通过设定一个虚位移，并计算压力所作的虚功，可以得到压力与位移的关系。

这对于液压和气压系统的分析和设计非常有用。

4.力学系统的能量分析：虚功原理在力学系统的能量分析中起着重要的作用。

通过设定一个虚位移，并计算力所作的虚功，可以得到物体的势能变化和动能变化，从而进一步分析力学系统的能量转化和守恒。

虚功原理的内容及应用条件1. 虚功原理的概念虚功原理是力学中的基本原理之一，它根据体系处于平衡状态时的平衡条件，从而推导出力学中的一些重要定理。

根据虚功原理，一个约束系统在平衡位置上的任意虚位移所做的虚功等于零。

虚功原理是可以应用在各个领域的一个重要原理，包括物理学、工程学等。

2. 虚功原理的条件虚功原理适用于满足以下条件的体系： - 约束体系：虚功原理主要应用于约束体系，即约束在某些条件下运动的物体体系。

- 平衡位置：虚功原理适用于约束体系处于某个平衡位置的情况。

- 虚位移：虚功原理建立在虚位移的基础上，即物体在平衡位置上的任意虚位移。

3. 虚功原理的应用虚功原理在力学中有广泛的应用，以下是几个常见的应用领域：3.1 静力学应用在静力学中，虚功原理可以应用于分析力的平衡和支持结构的设计等问题。

通过建立平衡方程和应用虚功原理，可以推导出约束体系的平衡条件和约束反力等。

3.2 动力学应用在动力学中，虚功原理可以用于分析非平衡状态下的物体运动。

通过应用虚功原理，可以推导出物体受力和加速度之间的关系，并得到物体的运动方程。

3.3 物体变形分析虚功原理还可以应用于物体的变形分析。

通过对物体进行虚位移，利用虚功原理和弹性力学理论，可以计算物体在受力作用下的变形情况。

3.4 热力学应用在热力学中，虚功原理可以应用于分析热力学平衡和传热等问题。

通过应用虚功原理，可以推导出热平衡条件和传热方程等。

3.5 其他应用领域除了上述应用领域外，虚功原理还可以应用于弹性体的弹性力学分析、流体力学中的动量守恒和能量守恒等问题。

4. 总结虚功原理是力学中的一个重要原理，它可以应用于各个领域的问题。

虚功原理适用于约束体系处于平衡位置的情况，并建立在虚位移的基础上。

通过应用虚功原理，可以推导出约束体系的平衡条件、力学关系和变形情况等。

虚功原理的应用广泛，包括静力学、动力学、热力学等领域。

了解虚功原理的内容及应用条件，对于深入理解力学和应用力学原理具有重要意义。

力学中的虚功原理在力学的广袤天地里，虚功原理宛如一颗璀璨的明珠，闪耀着智慧的光芒。

它不仅是解决力学问题的有力工具，更是深入理解物体运动和受力关系的关键钥匙。

要弄清楚虚功原理，首先得明白什么是“功”。

简单来说，功就是力在位移上的积累。

当一个力作用在物体上，并且物体在这个力的方向上发生了位移，我们就说这个力做了功。

比如，你推一个箱子，使它在水平方向移动了一段距离，你施加的推力就做了功。

那么，虚功又是什么呢？这可得好好说道说道。

虚功并不是真正意义上的功，它是在一个假设的、满足约束条件的微小位移下，力所做的功。

这个微小位移是想象出来的，并非实际发生的。

虚功原理的核心思想是：对于一个处于平衡状态的系统，所有主动力在任何虚位移上所做的虚功之和等于零。

这听起来可能有点抽象，咱们来举个例子。

想象一个简单的杠杆，支点在中间，两端分别挂着不同重量的物体。

当杠杆处于平衡状态时，如果我们给它一个微小的虚拟位移，那么两端重物的重力所做的虚功之和就是零。

为什么虚功原理这么重要呢？这是因为它为我们解决力学问题提供了一种简洁而有效的方法。

在很多实际情况中，直接分析力和位移的关系可能会非常复杂，但通过虚功原理，我们可以巧妙地避开这些困难。

比如说，在求解复杂的静定结构问题时，传统的方法可能需要我们详细分析每一个杆件的受力和变形，但利用虚功原理，我们可以把注意力集中在系统的整体平衡上，通过设定合适的虚位移，快速得出结果。

再比如，在分析机械系统的运动时，虚功原理可以帮助我们确定各个部件之间的力和能量关系，从而优化系统的设计和性能。

虚功原理还与其他力学原理有着密切的联系。

比如，它和达朗贝尔原理就有着深刻的内在一致性。

达朗贝尔原理通过引入惯性力，将动力学问题转化为静力学问题，而虚功原理则在这个转化过程中发挥了重要作用。

在实际应用中，我们需要注意一些问题。

首先，要正确地确定系统的约束条件，只有这样才能合理地设定虚位移。

其次，对于不同类型的力，如保守力和非保守力，在运用虚功原理时也有不同的处理方法。

虚功原理概念
虚功原理是力学中的重要概念，主要运用于静力学和弹性力学的问题中。

该原理是通过比较系统在实际情况下的受力和在虚位移情况下的受力之间的差异，来推导出力学问题的解析解。

虚功原理的基本思想是，如果一个力系统处于平衡状态，则在任意虚位移下，系统所受到的合力必然为零。

这意味着在虚位移下，系统没有做任何实际的功。

因此，可以根据虚功原理来解决平衡问题。

虚功原理的应用主要涉及到两个方面：平衡条件和变形计算。

在平衡条件中，通过比较系统在实际情况下的受力和在虚位移情况下的受力，可以得出力的平衡条件。

在变形计算中，可以通过比较系统在实际变形和虚位移情况下的变形能量，来计算系统的位移和应变。

虚功原理的使用需要考虑以下几个要点：
1. 虚位移应满足几何约束条件，即虚位移必须满足系统的边界条件和约束条件。

2. 虚功原理可以应用于单个物体或整个力系统，这取决于具体的力学问题。

3. 虚功原理可以推广到三维空间中的力学问题，并且可以应用于弹性体和非弹性体。

4. 虚功原理还可以推广到动力学问题，即考虑物体的运动和加速度。

总之，虚功原理是力学中非常重要的概念，可以用于平衡条件
和变形计算。

通过应用虚功原理，可以简化力学问题的分析，得到解析解。

力学系统的虚功原理与最小能量原理力学是研究物体运动和力的学科，虚功原理和最小能量原理是力学中的两个重要概念。

虚功原理是指在平衡状态下，外力对于系统所做的虚功为零；最小能量原理则是指在运动过程中，系统的能量达到最小值。

本文将介绍力学系统的虚功原理与最小能量原理，并探讨其在实际问题中的应用。

一、虚功原理虚功原理是力学中的一个重要原理，它描述了力学系统在平衡状态下外力对系统所做的虚功为零。

虚功原理的基本思想是，当系统处于平衡状态时，任何微小的虚位移所做的功都是虚功，而这些虚功的总和为零。

虚功原理的应用十分广泛。

例如，在静力学中，我们可以利用虚功原理来求解物体的平衡条件。

在弹性力学中，虚功原理可以用来推导物体的弹性形变和应力分布。

在动力学中，虚功原理可以用来推导物体的运动方程。

二、最小能量原理最小能量原理是力学中的另一个重要原理，它描述了力学系统在运动过程中系统的能量达到最小值。

最小能量原理的基本思想是，系统在运动过程中，会通过各种力的作用进行能量的转化，而系统的能量会趋向于最小。

最小能量原理的应用也非常广泛。

例如，在弹性力学中，我们可以利用最小能量原理来求解物体的弹性形变和应力分布。

在动力学中，最小能量原理可以用来推导物体的运动方程。

此外，在流体力学中，最小能量原理可以用来推导流体的运动方程和流速分布。

三、虚功原理与最小能量原理的联系虚功原理和最小能量原理在某种程度上是相互关联的。

虚功原理描述了系统在平衡状态下外力对系统所做的虚功为零，而最小能量原理描述了系统在运动过程中系统的能量达到最小值。

虚功原理可以看作是最小能量原理的一种特殊情况，即在平衡状态下系统的能量已经达到最小值。

虚功原理和最小能量原理的联系在实际问题中具有重要意义。

通过应用虚功原理和最小能量原理，我们可以求解物体的平衡条件、弹性形变、应力分布、运动方程等问题。

这些原理为我们研究力学系统提供了重要的理论工具。

总结起来，虚功原理和最小能量原理是力学中的两个重要概念。

1）刚体与弹性体的关系。

刚体是受力后没有变形的物体。

弹性体是指受力与变形成弹性关系的物体。

两者有本质的区别。

刚体没有变形能。

弹性体有弹性变形能。

（2）虚功与实功的关系。

如楼上的兄弟所说，虚功是使处于平衡状态下的物体发生“虚拟的”位移所需要的能量。

这与实功不同。

但是，我认为虚功和实功没有重大的差别。

也就是说，如果我们物体“真的”发生了这个位移，那么就所作的实功与虚功并无区别。

（3）我认为虚功原理最关键的部分并非“力的平衡”，而是能量的守恒。

这点实际上就是虚功原理的来源。

虚功的定义
体系上作用任意的平衡力系，又当体系发生符合约束条件无限小刚体体系的位移，则主动力在刚体上的需工为0，线弹变形体无非是刚体的叠加
而虚功真正的原理是体现在力的平衡上，而虚位移无非是在不违背平衡力下的位移。

而合功无任何关系，仅仅是量纲上一样。

同理可推出非线弹性体的虚功公式，就是根据截面平衡条件推出弹塑下截面的转角，然后代入弹性变形体的虚功公式即可，如矩形截面转角为应力/E*Y0。

力学中的虚功原理力学是物理学的一个重要分支，研究物体的运动和力的作用。

在力学的研究中，虚功原理是一个基本概念，它在解决力学问题时起着重要的作用。

本文将介绍力学中的虚功原理，并探讨其应用。

1. 虚功的概念和定义虚功是力学中的一个重要概念，它用于描述一个力对物体的作用所做的功，但物体实际上并未发生位移。

虚功可以通过以下公式计算：虚功 = 力 ×虚位移其中，力是作用在物体上的力，虚位移是物体在力的作用下所产生的虚拟位移。

虚位移是一个想象出来的位移，用于计算力对物体的作用所做的功。

虚功是一个标量，它的单位是焦耳（J）。

2. 虚功原理的表述虚功原理是力学中的一个基本原理，它描述了一个力对物体的作用所做的虚功等于零。

换句话说，当物体处于平衡状态时，力对物体的作用所做的虚功总和等于零。

虚功原理可以通过以下公式表述：Σ虚功 = 0其中，Σ虚功表示所有力对物体的作用所做的虚功的总和。

根据虚功原理，当物体处于平衡状态时，所有作用在物体上的力对物体所做的虚功总和为零。

3. 虚功原理的应用虚功原理在力学中有广泛的应用，以下是一些常见的应用场景：3.1 弹簧的伸缩虚功原理可以用于分析弹簧的伸缩问题。

当一个物体施加一个力使弹簧伸长或缩短时，虚功原理可以帮助我们计算弹簧对物体所做的虚功。

根据虚功原理，弹簧对物体所做的虚功等于零，即力与虚位移的乘积为零。

通过这个原理，我们可以求解弹簧的伸长或缩短距离。

3.2 斜面上的物体虚功原理还可以应用于斜面上的物体。

当一个物体沿着斜面上升或下降时，虚功原理可以帮助我们计算斜面对物体所做的虚功。

根据虚功原理，斜面对物体所做的虚功等于零。

通过这个原理，我们可以求解物体在斜面上的运动状态。

3.3 摩擦力的分析虚功原理还可以用于分析摩擦力的作用。

当一个物体在受到摩擦力的作用下运动时，虚功原理可以帮助我们计算摩擦力对物体所做的虚功。

根据虚功原理，摩擦力对物体所做的虚功等于零。

通过这个原理，我们可以求解物体在摩擦力作用下的运动状态。