虚功原理(物理竞赛)

高中物理竞赛辅导讲义 功能原理【基础知识】1、虚功法所谓虚功，就是假想某一个力做了一个微功。

“虚功法”，也叫“元功法”。

在物体处于静平衡的状态下，物体所受的合外力为零，在保持平衡的前提下，物体所受各个力的虚功总和为零。

用虚功法可以处理某些平衡问题，并且颇为简单。

2．伯努利方程如图所示，以流管中的ab 段理想流体为研究对象，在极短时间Δt （Δt →0）内，该段流体移至aꞌbꞌ，等效于aaꞌ之间的流体转移至bbꞌ之间，转移的流体质量Δm =ρS 1v 1Δt =ρS 2v 2Δt ，外力对该段流体做的功W =p1S 1v 1Δt −p 2S 2v 2Δt −Δmg (h 2−h 1)。

根据动能定理，有W = 12Δm v 22 − 12Δm v 12 即p 1S 1v 1Δt −p 2S 2v 2Δt −ρS 1v 1Δtg (h 2−h 1) = 12ρS 1v 1Δt (v 22−v 12) 整理得p 1+ρgh 1+12ρv 12 = p 2+ρgh 2+12ρv 22 即p +ρgh +12ρv 2=恒量，此式即为伯努利方程。

它表明，在惯性参考系中，当理想流体做定常流动时，一定流线上（或细流管内）各点的量p +ρgh +12ρv 2为一恒量。

流体水平流动时，或者高度差不显著时（如气体的流动）伯努利方程可表达为p +12ρv 2=恒量。

显然，在流动的流体中，压强跟流速有关，流速v 较大的地方压强p 较小。

【习题选编】1．如图所示，一轻质三足支架每边长均为l ，每边与竖直线成同一角度θ，三足置于光滑水平面上，且恒成一正三角形。

现悬挂一重为G 的重物，用一绳圈套在三足支架的三足上，使其不能改变与竖直线的夹角，试求绳中张力F T 。

2．如图所示，一个半径为R 的四分之一光滑球面置于水平桌面上。

球面上有一条光滑匀质软绳，一端固定于球面顶点A ，另一端恰好与桌面不接触，且单位长度软绳的质量为ρ。

求：（1）软绳A 端所受的水平拉力；（2）软绳所受球面的支持力；（3）软绳重心的位置。

虚功原理(物理竞赛)§2、虚功原理上次课主要是介绍了分析力学中经常要用到的一些基本概念，并由虚功的概念和理想约束的概念导出了解决静力学问题的虚功原理：0=⋅∑i r i F δ。

虚功原理适用的范围是：质点组，它适用的前提条件是只受理想约束。

这次课就举一些具体例子，使我们能够了解如何利用虚功原理去解决静力学问题。

三、应用虚功原理解题：例1、如图所示，有一质量为m ，长度为 的刚性杆子，靠在墙上，在与地面接触的B 端上受一水平向左的外力F ，杆子两端的接触都是光滑的，当杆子与水平地面成α角时，要使杆子处于平衡状态，问作用在杆子B 端上的力F 有多大？求F =？解：由题意可知它是一个静力学问题，而且接触都是光滑的，显然可以应用虚功原理来求解这个问题。

这个例子很简单，简单的题目往往能够清楚地说明物理意义，为了说明虚功原理的意义，如果一开始就举复杂的例子，由于复杂的数字计算将会掩盖物理意义，所以就以这个简单的例子来看看如何应用虚功原理来解出它。

第一步当然也是确定研究对象，即①选系统：在这个例题中，我们就取杆子为应用虚功原理的力学系统。

②找主动力：作用在我们所选取的系统上的主动力有几个？有两个。

一个是水平作用力F ，还有一个是重力m g 作用在杆子的质心上。

因为杆子两端A 、B 处的接触是光滑的，∴在该两处的约束力也就不必考虑。

③列出虚功方程：主动力找出来以后，视计算方便起见，适当选好坐标，并根据虚功原理列出虚功方程。

现在选取如图所示的直角坐标，于是我们现在就可列出系统的虚功方程。

列虚功方程时，正、负号是个很重要的问题，如果按虚位移的实际方向与力的方向间的关系确定虚功的正负号，很容易弄错。

为了不容易弄错，我们还是按力的作用点的坐标的正方向与力的方向间的关系来确定虚功的正负号。

这种方法既方便而又不容易搞错。

在列方程时必须要注意这个问题。

∵F 的方向与其作用点的坐标X 的正方向相反，∴F 取负而δX B 取正，∴此力的虚功为负的，即：0=--C B y mg x F δδ……①，由于虚功方程中的两个虚位移不是相互独立的，∴我们还需要将它们化成独立变量，然后才能令独立虚位移前的乘数等于零，从而求出最后的结果。

物理竞赛虚功原理小伙伴们！今天咱们来唠唠物理竞赛里超级有趣的虚功原理。

你知道吗？虚功原理就像是物理世界里的一个小魔法。

想象一下，有一个复杂的物理系统，各种物体相互作用着，就像一群小伙伴在打闹玩耍一样。

虚功原理呢，就像是一个超级聪明的小侦探，能在这个看似混乱的场景里找到一种特殊的平衡关系。

比如说，咱们常见的那些机械装置，像杠杆啊，滑轮组之类的。

在物理竞赛题里，它们可不会那么乖乖地让你轻松算出答案。

这时候，虚功原理就大显身手啦。

它就像是有一双特殊的眼睛，能看到那些隐藏在系统内部的微小变化。

你看，当我们给这个系统一个小小的“想象中的位移”，也就是虚位移的时候，就好像在这个机械装置的小世界里轻轻推了一把，看看会发生什么奇妙的事情。

虚功原理的厉害之处在于，它不管这个系统有多复杂，是由多少个小零件组成的。

就像一个万能钥匙，能打开各种物理系统平衡的大门。

它可不像有些方法，遇到复杂的情况就开始犯晕。

比如说，有些系统里有好几个力在同时作用，而且这些力的方向啊、大小啊还都不一样，这时候用常规的方法去分析平衡，那可真是头疼得很。

但是虚功原理呢，它就很潇洒，只要按照它的规则来，把每个力在虚位移上做的功算一算，然后根据虚功之和为零这个神奇的规则，就能轻松搞定平衡的条件啦。

我记得有一道物理竞赛题，是一个超级复杂的组合机械，里面有各种角度的杠杆，还有不同大小的滑轮。

当时我一看到那题，脑袋都大了。

但是当我想到虚功原理的时候，就好像突然找到了方向。

我就想象着给这个复杂的家伙一个小小的虚位移，然后开始计算每个力做的虚功。

这个过程就像是在玩一个解谜游戏，每算出一个力的虚功，就感觉离答案更近了一步。

当我根据虚功之和为零算出结果的时候，那种成就感简直无法形容，就像是找到了宝藏一样。

而且啊，虚功原理还能让我们从一个全新的角度去理解物理中的能量和功。

它让我们明白，在一个平衡的系统里，能量的分配是多么巧妙。

那些力虽然各自为政，但是在虚功原理的指挥下，却能和谐地达到一种平衡状态。

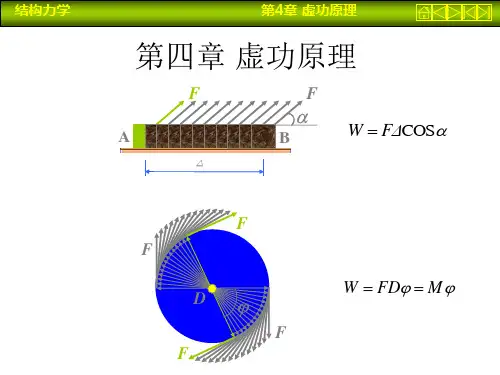
虚功原理单力作功力学上，一力F在其方向上产生位移始作功。

例如，下图所示之力F，以位置向量r说明其在路径s上之位置。

若力沿路径移至新位置r ' = r + d r，其位移为d r，而功dU为一纯量，以点积(dot product)定义如下dU= F⋅d r因d r为一微小量，其大小以ds表示，乃沿路径之微小弧长。

若d r与F尾端间夹角为θ，如上图，依点积之定义，上述方程式可写为dU= Fds cosθ上式功的表示式可以用二种不同方式予以说明：即F与位移在力之方向分量ds cosθ之乘积；或位移与力在位移方向之分量F cosθ之乘积。

若0≤θ≤90︒，则力分量与位移方向相同，功为正值；若90︒≤θ≤180︒，则两向量方向相反，功为负值。

又力与位移垂直，因cos90︒= 0，则dU = 0，或力作用在固定点上，因ds = 0，则功亦为零。

功之基本单位是力及位移之组合单位。

在SI系统，一焦耳(J)相当于1牛顿力使物体移动1米之位移所作之功(1 J = 1 N⋅m)。

在FPS系统，则功之单位为ft⋅lb (呎．磅)。

力矩与功之单位相同；但是力矩与功之观念毫无相关。

力矩为一向量，而功为一纯量。

力偶作功当力偶绕一与其作用面垂直之轴旋转时，此力偶作功。

考虑上图(a)中一物体受到一大小M = Fr之力偶作用。

物体任意微小位移可视为平移与旋转之组合。

物体平移时，沿力作用线方向之位移分量为ds t，如上图(b)所示，一力作正功( Fds t )，而另一力作负功(-Fds t )，两者相互抵消。

物体绕一与力偶作用面垂直且交于O点之轴旋转一微小角度dθ，如上图(c)。

(亦可考虑作用面上任意点)，图中各力均在其方向产生位移dsθ= ( r /2) dθ。

因此，二力作功为或dU = Mdθ若M与dθ方向相同则作正功，反之则作负功。

如同力矩向量，dθ之方向乃遵照右手定则(right-hand rule)，即右手四指为旋转方向而姆指指向即为dθ之方向。

1真实位形t 时刻δ力学竞赛辅导五 虚位移原理及其应用非自由质点系平衡，可以理解为主动力通过约束的平衡，因此平衡方程中必然要反映出约束的性质。

处理静力学的两种出发点：当质点系平衡时，主动力和约束力之间存在一定的关系，据此可建立主动力和约束力的平衡方程，即刚体的平衡条件。

它是任意质点系平衡的必要而非充分条件。

——刚体静力学（矢量力学）当质点系平衡时，在主动力和约束所容许的位移之间，也存在一定的关系，利用这些关系，可建立任意质点系平衡的充要条件。

——分析力学 一、基本概念1、约束：质点系中常存在一些限制各质点自由运动的条件，称这些条件为约束。

约束通常表现为质点系中质点的坐标、速度和时间的方程。

若n 个质点所形成的质点系受有k 个限制其位置的约束，那就有k 个表示这种约束的方程，因此，这时n 3个坐标中就只有k n -3个是独立的。

定常约束与非定常约束：前者约束性质不随时间而变，约束方程不显含时间：后者反之 运动约束：质点系在运动时受到的对运动条件(速度)的限制条件。

双面定常的几何约束（完整约束）：0),,,,,,,,,(n n n 222111=z y x z y x z y x f 非定常几何约束： 0)t ,,,,,,,,,,(n n n 222111=z y x z y x z y x f单面约束与双面约束：由不等式表示的约束称为单面约束，只能在单方向限制质点的位移或反之。

2小位移，称为该质点或质点系的虚位移。

它具有：1）假想的无限小位移，不需经历时间过程； 2）不破坏约束，可以不止一个； 3）与是否发生实际的运动无关。

虚位移与(无限小)实位移的关系： •实位移需要时间过程d t ，而虚位移不需要； •两者都要满足约束方程；•约束定常，可利用求无限小实位移的方法来求虚位移；•约束非定常，对实位移，约束方程所显含的时间t 为自变量，而对虚位移，2t 为常参量。

•虚位移用变分符号δ，无限小实位移用微分符号d ，虽然概念不同但它们都具有无限小的意义，因此，在定常约束情况下它们具有相同的数学运算规则。

§2、虚功原理上次课主要是介绍了分析力学中经常要用到的一些基本概念，并由虚功的概念和理想约束的概念导出了解决静力学问题的虚功原理：0=⋅∑i r i F δ。

虚功原理适用的范围是：质点组，它适用的前提条件是只受理想约束。

这次课就举一些具体例子，使我们能够了解如何利用虚功原理去解决静力学问题。

三、应用虚功原理解题：例1、如图所示，有一质量为m ，长度为 的刚性杆子，靠在墙上，在与地面接触的B 端上受一水平向左的外力F ，杆子两端的接触都是光滑的，当杆子与水平地面成α角时，要使杆子处于平衡状态，问作用在杆子B 端上的力F有多大？求F =？解：由题意可知它是一个静力学问题，而且接触都是光滑的，显然可以应用虚功原理来求解这个问题。

这个例子很简单，简单的题目往往能够清楚地说明物理意义，为了说明虚功原理的意义，如果一开始就举复杂的例子，由于复杂的数字计算将会掩盖物理意义，所以就以这个简单的例子来看看如何应用虚功原理来解出它。

第一步当然也是确定研究对象，即①选系统：在这个例题中，我们就取杆子为应用虚功原理的力学系统。

②找主动力：作用在我们所选取的系统上的主动力有几个？有两个。

一个是水平作用力F ，还有一个是重力m g 作用在杆子的质心上。

因为杆子两端A 、B 处的接触是光滑的，∴在该两处的约束力也就不必考虑。

③列出虚功方程：主动力找出来以后，视计算方便起见，适当选好坐标，并根据虚功原理列出虚功方程。

现在选取如图所示的直角坐标，于是我们现在就可列出系统的虚功方程。

列虚功方程时，正、负号是个很重要的问题，如果按虚位移的实际方向与力的方向间的关系确定虚功的正负号，很容易弄错。

为了不容易弄错，我们还是按力的作用点的坐标的正方向与力的方向间的关系来确定虚功的正负号。

这种方法既方便而又不容易搞错。

在列方程时必须要注意这个问题。

∵F 的方向与其作用点的坐标X 的正方向相反，∴F 取负而δX B取正，∴此力的虚功为负的，即：0=--C B y mg x F δδ……①，由于虚功方程中的两个虚位移不是相互独立的，∴我们还需要将它们化成独立变量，然后才能令独立虚位移前的乘数等于零，从而求出最后的结果。

（满分：200分）一、两个半球（ 分）如图，一个匀质球，质量为M，半径为R，沿过其球心的平面将其剖为两半。

再用轻绳沿着半腰捆起来放在光滑水平面上（绳与球间无摩擦）。

1）求匀质半球的质心与球心的距离x c；2）求绳中张力。

解答：1）直接积分可得：xc =xdmm=πR2−z2dzR23πR3=38R2）由虚功原理，有2×2TRδθ+Mgxcδ−sinθ=04TR−Mgx cδθ=0T=3Mg 32二、螺旋缩进（ 分）如图，在上半平面有均匀磁场，磁感应强度B沿z轴。

一个电荷量为q质量为m的粒子从原点沿y轴正向以速度v0入射上半平面。

粒子运动中同时受到一阻力作用，f=−αv，忽略重力的作用。

1) 若α能使粒子始终在上半平面运动，则其最小值αm应满足怎样的方程？2) 若α>αm，则粒子最终将趋近于上半平面的一点A，求其坐标。

解答：1) 粒子的运动方程为m dvdt =qv×B−αv全国中学生物理竞赛复赛模拟试题第十六套参考答案mv∙dvdt=qv∙(v×B)−αv21 2mdv2dt=−αv2v(t)=v0e−αm t令v t=v tτt, τ=1，有m dvdt=mdvdtτ+mvdτdt=qvBτ×k−αvτdτdt=qBmτ×kv t=v tτt=v t sinωt i+cosωt jω=qB mr t=mv0e−αm tα2+qB2−αsinωt−qB cosωt i+qB sinωt−αcosωt j+mv0(qBi+αj)α2+qB2易知，ωt=3π2时，r最接近x轴，从而αmqB=e−3π2αmqB2)令t⟶∞，得r=mv0(qBi+αj)α2+qB2三、导热管（28分）如图一个长圆柱形的均匀导热管，内半径和外半径分别为a,b。

初始时，铝、管的温度为T0，处处均匀。

将导热管置于一个环形热源环境中，热源对管施加一个径向向内的均匀能流，能流密度（单位时间内通过单位面积的热量）为J。

第15章 虚位移原理15-1 图示曲柄式压缩机的销钉B 上作用有水平力F ，此力位于平面ABC 内。

作用线平分ABC ∠。

设AB = BC ，θ2=∠ABC ，各处摩擦及杆重不计，求对物体的压缩力。

解：令B 有虚位移AB B ⊥r δ，而C 有铅直向上的虚位移C r δ，如图（a ）。

将B r δ及C r δ向BC 方向投影，为简单起见，以B r δ表示B r δ的绝对值B r δ，以C r δ表示C r δ，则有)902cos(δ)90cos(δ︒-=-︒θθB C r r即 θcos 21δδ=C B r r （1） 由虚位移原理得 0δsin δN =-C B r F r F θ θsin δδN F F r r C B = （2） 将式（1）代入（2）得 θtan 2N F F =15-3 挖土机挖掘部分示意如图。

支臂DEF 不动，A 、B 、D 、E 、F 为铰链，液压油缸AD 伸缩时可通过连杆AB 使挖斗BFC 绕F 转动，EA = FB = a 。

当︒==3021θθ时杆DF AE ⊥，此时油缸推力为F 。

不计构件重量，求此时挖斗可克服的最大阻力矩M 。

解：由虚功原理： 0δδcos 1=-⋅ϕθM r F A （1）式中 a r B δδ=ϕ （2）A 、B 的虚位移向AB 投影 22sin δcos δθθB A r r =2tan δδθB A r r = （3）式（2），（3）代入（1）得 0δδtan cos 21=⋅-⋅⋅a r M r F B B θθ Fa M Fa M 21,sin ,30221==︒==θθθ15-5 在图示机构中，当曲柄OC 绕O 轴摆动时，滑块A 沿曲柄滑动，从而带动杆AB 在铅直导槽K 内移动。

已知：OC = a ，OK = l ，在点C 处垂直于曲柄作用一力F 1；而在点B 沿BA 作用一力F 2。

求机构平衡时F 2与F 1的关系。

解：用解析法解，选取ϕ为广义坐标，则滑块A 的约束方程ϕtan l y A =ϕϕδsecδ2l y A = （1） 由虚位称原理 0δδ)(21=+-A y F a F ϕ （2）把式（1）代入（2）得 0δsec δ221=+-ϕϕϕl F a F因 0δ≠ϕ，于是有 0sec 221=+-ϕl F a F故 ϕ221cos a l F F =15-7 图示滑套D 套在光滑直杆AB 上，并带动杆CD 在铅直滑道上滑动，已知︒=0θ时弹簧为原长，弹簧刚性系数为5 kN/m 。

电容的定义是：找到两块金属板（等势面），令其中一块带上 +Q ，一块带 -Q ，这时候两极板电势差为U ，电容 C = Q 。

如果只说某个物体的电容，一般把大地当作另一个极板。

这也就形成了我们 U 求电容的一般思路：给定电势求电荷；给定电荷求电势。

注意：讲电容的时候，我们总要求一个极板 上发出的电场线回到另一个极板，这也就保证了两个极板上电荷大小相等。

常见的几种电容例如平行板电容、球型电容、同心圆柱电容、同心球电容等是基本知识点，应当 熟练掌握。

【例1】 两块正方形的极板，边长为 L ，相对放置，间距为 d 构成电容器，d << L 。

各充电 ±Q 之后保 持绝缘。

求做如下操作之后两个极板之间的电势差。

a) 将极板沿着一条边错动小距离 ∆Lb) 将一个极板绕着一条边转动一个小角度θ ，并使得 θ L << dc) 一个小金属球，半径为 r << d ，质量为 m （重力可以忽略）。

开始位于一个极板负极内侧，由于静电感应作用，带上负电，然后受到电场力作用飞向正极板，发生非完全弹性碰撞并重新达到经典平衡。

经过时间 t 之后，求两极板之间的电势差。

两个极板间的被放上其他电荷，电荷的受力为 F = Eq 。

如果考虑极板自己的受力，则 F = Eq 。

2我们知道，在考虑一个电荷受力时，不能算自己的电场，所以在考虑某极板的受力时，只能算另一极 板产生的电场，刚好为两极板间电场的一半。

同时由高斯定理易得，无穷大板产生的电场为 E = 2π k σ 。

通过电流做功的定义，很容易得出，电容器储存能量的公式为：E = 1CU 2 = 1 Q2 2 C 还有另一种理解电容器储存能量的方式：电荷之间并不是直接相互作用，而是通过电场相互作用； 这样也就理所当然不存在电荷间相互作用能，作用能包含在空间的电场中。

在这样的观点中，我们可电容里的受力与能量电容电压电荷知识点睛高二物理竞赛第2讲电容、电介质、电能2以得到相互作用能在空间中分布的密度度：即能量由电场携带。

力学中的虚功原理力学是物理学的一个重要分支，研究物体的运动和力的作用。

在力学的研究中，虚功原理是一个基本概念，它在解决力学问题时起着重要的作用。

本文将介绍力学中的虚功原理，并探讨其应用。

1. 虚功的概念和定义虚功是力学中的一个重要概念，它用于描述一个力对物体的作用所做的功，但物体实际上并未发生位移。

虚功可以通过以下公式计算：虚功 = 力 ×虚位移其中，力是作用在物体上的力，虚位移是物体在力的作用下所产生的虚拟位移。

虚位移是一个想象出来的位移，用于计算力对物体的作用所做的功。

虚功是一个标量，它的单位是焦耳（J）。

2. 虚功原理的表述虚功原理是力学中的一个基本原理，它描述了一个力对物体的作用所做的虚功等于零。

换句话说，当物体处于平衡状态时，力对物体的作用所做的虚功总和等于零。

虚功原理可以通过以下公式表述：Σ虚功 = 0其中，Σ虚功表示所有力对物体的作用所做的虚功的总和。

根据虚功原理，当物体处于平衡状态时，所有作用在物体上的力对物体所做的虚功总和为零。

3. 虚功原理的应用虚功原理在力学中有广泛的应用，以下是一些常见的应用场景：3.1 弹簧的伸缩虚功原理可以用于分析弹簧的伸缩问题。

当一个物体施加一个力使弹簧伸长或缩短时，虚功原理可以帮助我们计算弹簧对物体所做的虚功。

根据虚功原理，弹簧对物体所做的虚功等于零，即力与虚位移的乘积为零。

通过这个原理，我们可以求解弹簧的伸长或缩短距离。

3.2 斜面上的物体虚功原理还可以应用于斜面上的物体。

当一个物体沿着斜面上升或下降时，虚功原理可以帮助我们计算斜面对物体所做的虚功。

根据虚功原理，斜面对物体所做的虚功等于零。

通过这个原理，我们可以求解物体在斜面上的运动状态。

3.3 摩擦力的分析虚功原理还可以用于分析摩擦力的作用。

当一个物体在受到摩擦力的作用下运动时，虚功原理可以帮助我们计算摩擦力对物体所做的虚功。

根据虚功原理，摩擦力对物体所做的虚功等于零。

通过这个原理，我们可以求解物体在摩擦力作用下的运动状态。

说明：1、2016版和2013版相比较，新增了一些内容，比如☆科里奥利力，※质心参考系☆虚功原理，☆连续性方程☆伯努利方程☆熵、熵增。

另一方面，也略有删减，比如※矢量的标积和矢积，※平行力的合成重心，物体平衡的种类。

有的说法更严谨，比如反冲运动及火箭改为反冲运动※变质量体系的运动，※质点和质点组的角动量定理(不引入转动惯量) 改为质点和质点组的角动量定理和转动定理，并且删去了对不引入转动惯量的限制，声音的响度、音调和音品声音的共鸣乐音和噪声增加限制（前3项均不要求定量计算）。

2、知识点顺序有调整。

比如刚体的平动和绕定轴的转动2013版在一、运动学的最后，2016版独立为一个新单元，---很早以前的版本也如此。

3、2013年开始实行的“内容提要”中，凡用※号标出的内容，仅限于复赛和决赛。

2016年开始实行的进一步细化，其中标☆仅为决赛内容，※为复赛和决赛内容，如不说明，一般要求考查定量分析能力。

全国中学生物理竞赛内容提要(2015年4月修订，2016年开始实行)说明：按照中国物理学会全国中学生物理竞赛委员会第9次全体会议(1990年)的建议，由中国物理学会全国中学生物理竞赛委员会常务委员会根据《全国中学生物理竞赛章程》中关于命题原则的规定，结合我国中学生的实际情况，制定了《全国中学生物理竞赛内容提要》，作为今后物理竞赛预赛、复赛和决赛命题的依据。

它包括理论基础、实验、其他方面等部分。

1991年2月20日经全国中学生物理竞赛委员会常务委员会扩大会议讨论通过并开始试行。

1991年9月11日在南宁经全国中学生物理竞赛委员会第10次全体会议通过，开始实施。

经2000年全国中学生物理竞赛委员会第19次全体会议原则同意，对《全国中学生物理竞赛内容提要》做适当的调整和补充。

考虑到适当控制预赛试题难度的精神，《内容提要》中新补充的内容用“※”符号标出，作为复赛题和决赛题增补的内容，预赛试题仍沿用原规定的《内容提要》，不增加修改补充后的内容。