当前位置：文档之家 › 自然坐标·切向和法向加速度

自然坐标·切向和法向加速度

  • 格式：ppt
  • 大小：1.36 MB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

自然坐标系

自然坐标系


r

t
t 0
AB .
t R
ern
v2 R
en
法向加速度
a

an

v2 R


vB

B vA
R

O
A
大小，方向，作用
2. 一般圆周运动的
切向加速度和法向加速度 分析方法
vB r
v vB vA vrn vr v
vrn 表示速度方向改变量 vr 表示速度大小改变量
lim lim vr
t 0
rr t
t 0
s t
er

ds dt
er


ds dt
三、 自然坐标系下的加速度
1. 匀速圆周运动， 法向加速度
v vB
vA

v vB
vA
Δv vB vA ,

AB R
lim lim ar
t 0
则：a an2 a 2 (1.88)2 (1.2)2 2.23(m / s2 )
tg an
a
12233'
总结解题策略：
（1）分析问题特点，建立恰当的坐标系 （2）由运动方程求解速度随时间变化的表达式 （3）分别计算出切向加速度与法向加速度，再 求解合加速度的大小和方向
解：根据加速度的定义：
ar
anern
a er

v2 R
ern

dv dt
er
a an2 a 2
v

ds dt
2
R
a

d
dt
1.2t
2013-01-2自然坐标系下的速度-加速度

2013-01-2自然坐标系下的速度-加速度


a
a
0，an
a
an
0
为匀速率曲线运动（圆 周运动）
dv dt
0
v2
n0
a an
a
a a a 2 an 2 dv dt2 v2 2
加速度总是指向曲线的凹侧
大学物理
自然坐标系中总加速度为：
a a an
改变速度大小
大小 a a 2 an2
加速度
方向 tan 1 an
下面三种情况分别代表那一类运动？
１. ，an＝0， a 0, 2. ＝常量，an 0，a＝0, 3. ＝常量，an 0，a 0,
１. 变速直线运动 ２. 匀速率圆周运动 ３. 变速率圆周运动
大学物理
讨论
质点沿固定的圆形轨道， 若速率 v 均匀增加，at 、an、
a以及加速度与速度间的夹角中哪些量随时间变化？
v lim r
t0 t
ds
dt
vr ds v v v
dt
z
v
p s
s
r q
r(t)
r(t t)
o
y x
自然坐标系下的 速度表达式
大学物理
讨论物理意义：
vr ds v v v
dt
ds v dt
1、 瞬时速率 v：
反映了质点任一时刻沿轨道运动的快 慢。
2、任何时刻质点的速度总沿轨道的 切线方向，速度只有切线分量而无法 向分量。
与切向加速度垂直
大学物理
例题
一质点沿半径为R的圆周按规律 s v0t b运t 2动/ 2，
v0、b 都是正的常量。求：
（1） t 时刻质点的总加速度的大小
（2） t 为何值时，总加速度的大小b
自然坐标系中的加速度分量

自然坐标系中的加速度分量


任务 自然坐标系中的加速度分量
质点沿已知平面轨道曲线运动,速度 沿轨道切线方向, 则将加速度分解为切向分量和法向分量。
nn
a
dv
d
(v) v v
dt dt
v
vn
v
v
ds
d
n
d v
v2
n
dt ds
dt
任务 自然坐标系中的加速度分量
a
dv
v2
n
dt
a a ann
曲线的曲率半径为：
运动轨迹是空间曲线，在曲线的M点作切线和割线， M点的
切线和割线在空间确定一个平面，当无限趋近时，切线和割
线确定的极限平面称为点的密切面。在密切面内过M点垂直
于切线的直线称为主法线，既垂直于切线又垂直于法线的直
线称为副法线。
b
n
任务 自然坐标系中的加速度分量
按照平面情况的方法，可以得到
aan
dv v2
dt
ab 0
质点的运动轨迹是空间曲线时，加速度总是在密切面内。
任务 自然坐标系中的加速度分量
1）.平面自然坐标系
质点沿着曲线轨道运动时，其速 度和加速度与轨道的几何形状有关。 如果我们以质点的起始位置为坐标原 点，以轨道曲线的弧长为坐标，则弧 坐标s就唯一确定了质点的位置。在 质点的平面运动中，曲线上任意一点 P的切线和法线构成P点的正交坐标系， 称为自然坐标系。
a
dv dt
s v
an
v2
s2
（切向加速度） （法向加速度）
大小
a
a2 an2
v2 ( v2 )2
a 是由于速度的量值改变所引起的
an 是由于速度的方向改变 自然坐标系中的加速度分量
切向加速度和法向加速度

切向加速度和法向加速度


r τ (t)
τ
r
θ
θ + θ
x
r τ r θ ： 大小 τ = 2sin 2 ≈ θ
dτ dτ dθ dτ dθ ds dτ r ds = ρ ds =V = = , =n , dθ , dt dt dθ dt dθ ds dt dθ
r τ ≈ θ n r r r dτ r τ θ n r lim θ →0, θlim θ = θ →0 θ = n dθ = n →0
α
r a
an
dV 2 V 2 2 2 a = at2 + an = ( ) + ( ) , tgα = an / at dt ρ
讨论：（1 直线运动， 讨论：（1）直线运动，ρ = ∞, an = 0 ：（ dV V2 a = 0, an = 匀速率圆周运动， （2）匀速率圆周运动， t = ：向心加速度 R dt 一般曲线运动及变速率圆周运动， （3）一般曲线运动及变速率圆周运动，at ≠ 0, an ≠ 0 V2 V2 （4） an = ρ= ：计算曲率半径
θ = 63.4o
第6节 节
圆周运动的角量表示
角坐标， s = Rθ θ ：角坐标，rad θ = θ (t) s = s(t)
y
r P r s θ A R O
V = ωR,
dω d 2θ ：角加速度， 角加速度， rad / s2 β= = 2 dt dt V 2 ω2 R2 = = ω2 R at = Rβ, an = R R
第5 节
相对运动
P
r r
S
O
静系
r r0
S′
O′
动系
r r′
r r r r = r ′ + r0 r r r dr dr ′ dr0 = + dt d = r′ + r0
圆周运动和一般曲线运动

圆周运动和一般曲线运动


x
vx v0 cos vy v0 sin gt
v (v0 cos )i (v0 sin gt) j
v dr dt
r
v0t cos
i
v0t
sin
1 2
gt 2
j
j
y
v0t
1 gt 2 2
gt 2
1 2
sin t
0
v
r
O v0 cost i
r
v0t
cos
i
v0t
sin
1 2
'K
aPK aPK ' a K'K
绝对时空观只在 v << c 时才成立。
2.不可将速度的合成与分解和伽利略速度变 换关系相混。
速度的合成是在同一个参考系中进行的， 总能够成立；
伽利略速度变换则应用于两个参考系之间，
绝对时空观只在 v << c 时才成立。
例1－7：一货车在行驶过程中，遇到5m/s竖直下落的
v02
gx2 cos2
射程
H
xm
v02 g
sin
2
射高
h
ym
v02 2g
sin2
y
ym
v0
O H
h
xm x
H
xm
v02 g
sin 2
射程与发射角的关系
§1－3 相对运动 常见力和基本力
主要内容：相对运动 重点要求：掌握伽利略变换，相对运动的观点
典型例题：相对运动
数学方法：矢量分析
一、伽利略变换
O R
en
et
P
方向都变化
et '
et
1.5 加速度 切向和法向加速度

1.5 加速度 切向和法向加速度


et

v2

en

v0 2 r
en
r
x
o
(2)如图,设质点在 t=0 时位于 x=r ,
y=0 x
r
cos
v0
t
,
y r sin v0 t
r
r
r rer
vx

dx dt

v0
sin
v0 r
t
,
vy

dy dt

v0
c os v0 r
t
ax

dvx dt
v02 r
v
的方向跟

det v d
dt dt


et 垂直，即 en
en

ven
v2

的方向
en
a

dv dt
et

v2

en

at et
anen

p1 et (t) p2
d
et (t dt)

et (t)
d det

et (t dt)
匀速直线运动 匀变速直线运动 匀速率圆周运动 变速曲线运动
at
a an
4
例2、设一质点在半径为r的圆周上以速率v0运动， 试写
出：（1）在自然坐标系中质点的速度、切向和法向加
速解度：；（（12））在直v 角v坐0 e标t 系中质点的速度和加速y度分 量v0。t
a

dv dt
加速度 切向加速 度和法向加速度
1
一、加速度
平均加速度：a v
(2)自然坐标、圆周运动、相对运动

(2)自然坐标、圆周运动、相对运动


移动他在车中的位置就能接住球，则抛出的方向与竖直
方向的夹角应为多大？ 解：抛出后车的位移：
v0球对车
x1
v0t
1 2
at 2
a
球的位移：
x2 (v0 v0' sin )t
V0
车对地
y2
(v0'
cos
)t
1 2
gt 2
（2）自然坐标、圆周运动、相对运动
小孩接住球的条件为：x1=x2; y=0
1 2
vA
t
0 atdt
（2）自然坐标、圆周运动、相对运动
已知：vA 1940km h1 vB 2192km h1
t 3s AB 3.5km
vvAB vdv 0t atdt
在点 B 的法向加速度
A
v A
at
an
vB vA 23.3m s2
vB2
t
106m
s
2
r
在点 B 的加速度
r an
（2）自然坐标、圆周运动、相对运动
一、曲线运动：自然坐标、切 向加速度和法向加速度 二、圆周运动与角量系统 三、相对运动
v' v
B
n A
n
y v' y'
u
B 60 A
u
o'
x'
o
x
y
B
r A
o
x
（2）自然坐标、圆周运动、相对运动
一、自然坐标、平面曲线运动
自然坐标系 (natural coordinates)
（D）若物体作匀速率运动，其总加速度必为零
a （E）若物体的加速度 为恒矢量，它一定作
用自然坐标表示平面曲线运动中的速度和加速度

用自然坐标表示平面曲线运动中的速度和加速度


解 ds
vx2
v
2 y
v z2dt
A 2 cos2 t A 2 sin2 t B2 dt
s
s
ds
t
A2 2 B2dt
0
0
v
vτ

dsτ

A2 2

B2
τ
dt
A2 2 B2t
例 将一根光滑的钢丝弯成一个竖直平面内的曲线，质点可沿
当 t 0 时
τ (t)
τ

τ (t)
θ θ
τ
//
n
θ
τ
τ
θ
n

τ (t t)
因而 dτ lim τ lim θ n lim θ s n 1vn dt t0 t t0 t t0 s t ρ
O 参考物

( lim
r
τ)
ds
dsτ
vτ
t0 s dt dt
速度矢量在切线上的投影
二. 加速度
v

dsτ

vτ
dt
a

dv dt

d dt
(dsτ) dt

d2s dt 2
τ

ds dt
dτ dt
第一项：d2s dt 2
τ
叫切向加速度
aτ
dy P ds
Ox
sin ds dy
v v0
vdv


y y0
gdy

v2

v
2 0
2g( y0

y)
径的圆弧所构成
曲线运动的法向和切向加速度

曲线运动的法向和切向加速度


x

an
a
y
2
g
2
dv gt a 2 dt v0 g 2 t 2
与速度同向
an g a
2
v0 g v0 g 2 t 2
2
与切向加速度垂直
圆周运动的角量描述
v2
v B 1 A s R

O
A t t t B
X
角位置 角位移

沿逆时针转动，角位移取正值 沿顺时针转动，角位移取负值
两类运动学问题
1、已知运动方程，求速度、加速度 求导数 2、已知加速度和初始条件，求速度和运动方程 运用积分方法 注意 讨论问题一定要选取坐标系 注意矢量的书写
r r r r dr , ds, dv , dt 与Vr ,Vs,Vv ,Vt 的物理含义
• 1.自然坐标系：就是将坐标原点固定在运动 质点上，取质点的速度方向（曲线的切线方 向）为一个坐标轴（切向轴）的正方向，其 单位矢量用 表示，取与切向正交、且指向 曲线的凹侧的法线方向为另一个坐标轴（法 向轴）的正方向，其单位矢量用 n 表示。由 于这种坐标系的切向坐标轴和法向坐标轴会 随着质点的运动自然变换方向，故叫做自然 坐标系。
(2)子弹在t时刻的速度，切向加速度和法向加速度。
解：(1)
x v0 t 1 2 y gt 2
o
v0
x

an
a
1x g y 2 2 v0
2
y
g
(2)
vx v0 , v y gt
v v x v y v0 g t
gt arctg v0
2 2 2 2 2
o
v0
dv v a n dt R
切向加速度和法向加速度

切向加速度和法向加速度


dV 2 at 1 / 9 0.111(m / s ) dt
9
t =2（分）=120s，
V =120/9(m/s)
V2 an 0.222m / s 2 R
a a a 0.248m / s , tg an / at 2, 63.4
2 t 2 n 2
V V0 at
**********************************************************************************
d (
0

t
0
t )dt
1 2 角位移： 0 0t t 2 2 2 0 2 ( 0 )
匀速圆周运动 匀速直线运动
0
**********************************************************************************
第5节
相对运动
r
S
O
静系
P
r0
S
O
动系
r
r r r0 dr dr dr0 dt dt dt
S 相对于 S 作平动运动 r r r0
dr V ：质点在 S 系中的速度（绝对速度） dt dr V ：质点在 S 系中的速度（相对速度） dt dr0 V0 ：O 点相对于 O 点的速度（牵连速度） dt
VB对A VB VA
dV dV dV0 dt dt dt
aB对A aB aA
例：汽车以20
m/ s
03运动学圆周运动自然坐标系角速度角加速度切向加速度法向加速度

03运动学圆周运动自然坐标系角速度角加速度切向加速度法向加速度

§1-3 圆周运动
1 圆周运动的角量描述：质点做圆周运动时，轨道上 的任意点到圆心距离为R,用一个变量θ即可描述其运动。
Y
r
r =R
θ确定后：x=Rcosθ
θ=θ(t)
y=Rsinθ
X 定义：角位置 θ 单位 rad 弧度
角位移△θ=θ（t+ △t) -θ(t)
平均角速度
瞬时角速度 (SI)单位：rad/s 弧度/秒
v
dr dt
Y
R sin
V
d
dt
ቤተ መጻሕፍቲ ባይዱ i
R cos
d
dt
j
R d
R
d
( sin i
cosj )
dt
[cos(
)i
sin(
)
j]
r
dt
2
2
括号中的项是与r垂直的单位矢量
X 速度大小为 v=Rω
方向在圆周的切线方向上。 4
同样可以得到加速度：
a
R
d
(sini cosj) R( cos
d
t
lim d
t0 t dt
工程单位 rev/min(转/分）
1
平均角加速度
t
瞬时角加速度 lim d
t0 t dt
(SI)单位：rad/s2 角速度与角加速度都是矢量，角速度的方向由右手定 则确定。（规定用右手螺旋定则来判定：四指方向为 绕向，大拇指方向为角速度方向！！ ） α与ω同向。质点作加速圆周运动。
vy
vx
g at
an
v
Vy=V0sinθ-gt= -5.46m/s
V Vx2 Vy2 15.13m / s
an=gcos γ =gV x/V=9.13m/s2

切向和法向加速度.ppt

2 2 t
dv at dt
2 v0 g 2t 2
an g a
v0 g v g t
2 0 2 2
与速度同向
与切向加速度垂直
例2、一质点在oxy平面内作曲线运动，其加速 度是时间的函数。已知ax=2, ay=36t2。
设质点t＝0时r0=0,v0=0。求：(1)此质点的运动 方程；(2)此质点的轨道方程，(3)此质点的切向 加速度。
两式相比得：
a tan g
a tan g
1
d 5.横向速度V : v r dt
三.
应用:
1.在有心力运动中,常用极坐标系.
这将在第四章接触到.
2.在圆周运动中,以圆心为极点,
Vr 0 d V r r dt
则r=恒量,所以圆周运动:
对极坐标系的知 识,只要求了解
§2.8
伽利略变换 和相对运动
一、相对运动
研究的问题: 在两个惯性系中考察同一物理事件 实验室参照系 相对观察者固定
以上也称为伽利略相对性原理，力学相对性原理。
如：动量守恒定律
S
m1v1 m2v2 m1v10 m2v20
v1 m2 v2 m1 v10 m2 v20 S m1
例 哈勃定理与宇宙膨胀 已知，各星系远离我们而去，退行速度正 比于距离（哈勃定理）。
o
x
a
(x′)
r x, y, z, t v x, y, z, t r x, y, z, t v x, y, z, t
a
1.位矢的坐 标分量式：
y
S
u
r
O′
S’

01-2自然坐标系中的描述及相对运动


(1) a 0 匀速率运动； a 0 变速率运动
(2) an 0 直线运动; an
0
曲线运动
第二讲 自然坐标系：切向加速度和法向加速度、相对运动
例1.由楼窗口以水平初速度v0射出一发子弹，取枪 口为原点，沿v0为x轴，竖直向下为y轴，并取发射 时t=0.试求： (1)子弹在任一时刻t的位置坐标及轨道方程； (2)子弹在t时刻的速度，切向加速度和法向加速度。

C
v2
法向加速度大小等于速率平方除以曲率半径， 方向沿轨道的法线指向。
第二讲 自然坐标系：切向加速度和法向加速度、相对运动
dv v a a an n dt
a a
2
a an

a
a an
2 2 2
2
2 v dv dt
2 2
相对性：参照系、坐标系
直角坐标
22Leabharlann 2222
x
x
x
x
x
第二讲 自然坐标系：切向加速度和法向加速度、相对运动
2-1. 在自然坐标中描述质点的运动
1. 位置：在轨道上取一固定点O，用质点距离O的路程
长度 s，可唯一确定质点的位置。位置 s有正负之分
2. 位置变化: s 3. 速度： 沿切线方向。
解：(1) x v0 t
2
1 2 y gt 2
o
v0
x

1 x g y 2 2 v0
an
y g
a
第二讲 自然坐标系：切向加速度和法向加速度、相对运动
(2) v x v0 , v y gt
o
2 0 2 2

2 6_自然坐标·切向和法向加速度

2 6_自然坐标·切向和法向加速度
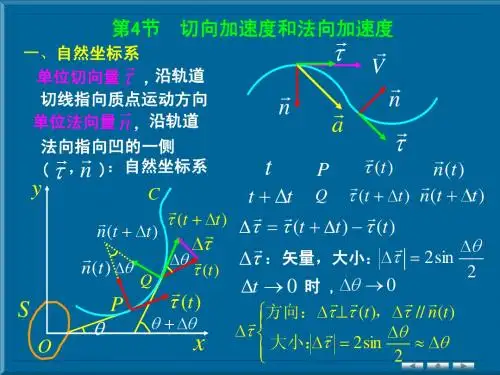
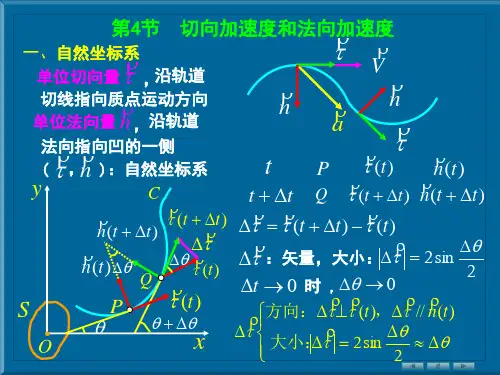
自然坐标：
在机械系统中，物体运动的轨迹往往是复杂的曲线，假设物体在曲线上运动。

我们可以根据物体在曲线上的位置，将坐标系重新定义，使之简化成两个自由度。

这样，物体的位置就可以用曲线上的一个参量来描述，这个参数称为自然参数；在这个参数的变化下，这个物体距离运动曲线的距离是不会改变的。

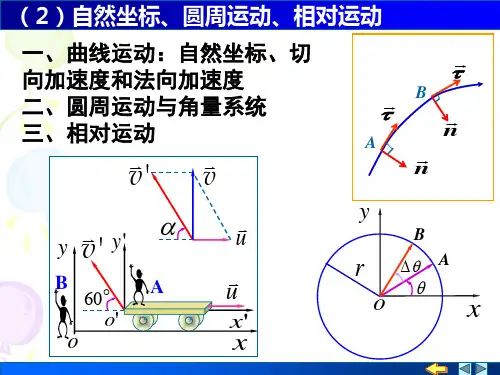
自然坐标系便是以这个自然参数为一坐标，另一个坐标是位置垂线于切线的方向，一般叫切线坐标，或称为法线坐标。

对于物体在曲线上的运动，根据牛顿第二定律，物体的加速度可以拆解成沿着曲线切向和法向的两个方向的加速度。

切向加速度：
物体在曲线上运动时，有一个切向的加速度，即切线方向上的加速度。

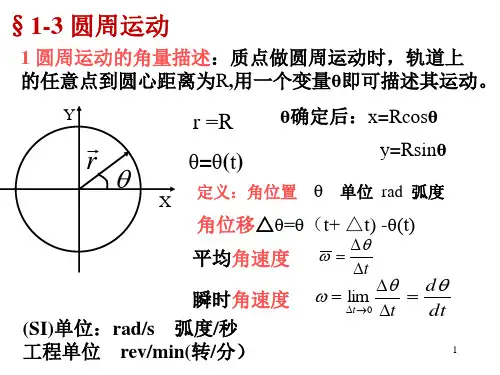
在自然坐标系中，我们可以通过物体在曲线上的两个连续位置的坐标求出物体在曲线上运动时的切向单位向量，然后对物体的速度向量进行投影，就可以求出物体在切向方向上的分量，进而求出物体在切向方向上的加速度。

$$a_t = \frac{d}{dt}\left(\frac{ds}{dt}\right) = \frac{d^2s}{dt^2}$$
其中，$a_t$代表切向加速度，$s$表示曲线的自然参数，$t$表示时间。

$$a_n = \frac{v^2}{\rho}$$
其中，$a$表示物体在曲线上的总加速度。

圆周运动的切向加速度和法向加速度 角加速度

如 t 0 时, 0, 0
0 0t 12t2
2
2 0
2 (
0)
对于作曲线运动的物体，以下几种说法中哪一 种是正确的：
（A）切向加速度必不为零；
（B）法向加速度必不为零（拐点处除外）；
（C）由于速度沿切线方向，法向分速度必为零， 因此法向加速度必为零；
（D）若物体作匀速率运动，其总加速度必为零；
周运动 , 若不计重力加速度的影响, 求: (1) 飞机在点B
的加速度; (2)飞机由点A 到点B 所经历的路程 .
A
v A
解（1）因飞机作匀变速率
运动所以 at 和 为常量 .
r an
o
a
B
at
v B
at
dv dt
分离变量有
vB dv
vA
t
0 atdt
已知：vA 1940km h1 vB 2192km h1
an
已知： vA 1940km h1 vB 2192km h1
（2）在时间
t 3s
t 内矢径
r
AB 3.5km
所转过的角度
为
A
v A
At
1t 2
2
飞机经过的路程为
r an
o
B
a
at
v B
s
r
v At
1 2
att
2
代入数据得
s 1722m
v
ds dt
et
vet
ret
质点作a 变 速ddvt率圆d周dvt运e动t 时v
det dt
切向加速度
v2 et2
o
r
evt11
at
dv dt

1.3.1自然坐标切向加速度和法向加速度


an
v
2r
v2 r
v2
et 2
v1
o
r
et1
v
v 2
v1
1.3给定轨道的平面曲线运动
圆周运动加速度
a a
at
an
ret rω
2en
大小 a at2 an2 方向 θ tan1 an
at
y
a
en vet
o
x
1.3给定轨道的平面曲线运动
线量和角量的关系
ds Rd
v ds R d R
a
dv dt
et
v2
en
at et
an en
1.3给定轨道的平面曲线运动
1.3.2 圆周运动
角坐标 (t) 角位移
角速度
lim d
t0 t dt
y
B
r A
o
x
速率
v lim Δs r lim Δθ
Δt0 Δt
Δt0 Δt
v(t) r(t)
速度
v
veddt stert et
切向单位矢量的时间变化率
det dt
det dt
dθ dt en
法向单位矢量
a ddvt et ven
法向加速度
v2
et 2
v1
o
r
et1
et
et
2
et1
1.3给定轨道的平面曲线运动
a
dv dt
et
ven
切向加速度(速度大小变化)
at
dv dt
r
d2s dt 2
法向加速度(速度方向变化)
1.3给定轨道的平面曲线运动
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

[解] v ds 30 10t
dt
an

v2

at

dv dt
B
A
30
O 15
C
t =2 s = 80m v = 50m/s
上页 下页 返回 结束
第二章 质点运动学 [例题4] 由楼窗口以水平初速度v0射出一发子弹，取枪口 为原点，沿v0为x轴，竖直向下为y轴，并取发射时t = 0. 试求： (1)子弹在任一时刻t 的位置坐标及轨道方程； (2)子弹在t 时刻的速度，切向加速度和法向加速度.
Δ1v

vΔ

an
lim Δt 0
Δ1v Δt

v
an

ven


2
Ren
上页 下页 返回 结束
第二章 质点运动学
(3)切向加速度
t0 时，近似有 v' // v // Δ2v
Δ2v

[v'v
]et

Δvet
at

lim
Δt 0
Δ2v Δt
任何矢量都可向切向和法向方向作正交分解.
§2.6.2 速度·法向和切向加速度
动画演示
1. 速度和加速度矢量
速度矢量 加速度矢量
v v et
a at an atet anen
at和an分别为质点的切向加速度和法向加速度.
上页 下页 返回 结束
第二章 质点运动学
求汽车在t=1s时的加速度.
[解] 加速度
a anen atet
an vt2 R
vt

ds dt

20 0.6t 2
at

d2s dt 2
an

(20
0.6 t 2 )2 R
at 1.2t
上页 下页 返回 结束
第二章 质点运动学
将R=200m及t＝1s代入上列各式，得
vt (20 0.612)m s 19.4m s
an

(19.4)2 200
m
s2
1.88m
s2
at 1.21m s2 1.2m s2
a an2 at2 (1.88)2 (1.2)2 m s2 2.23m s2
tan an 1.88 1.5667
at 1.2
12233'
为加速度与
et
的夹角.
上页 下页 返回 结束
第二章 质点运动学
[例题2]低速迫击炮弹以发射角45度 发射,其初速率v0=90m/s. 在与发射点同一水平面上落地.不计空气阻力,求炮弹在最高 点和落地点其运动轨迹的曲率.
[解]将炮弹视为质点,不计空气阻力. 在直交坐标系O-xy中,
如图选轨迹上一点 O为原
O
点，用由原点 O 至质点位 s<0 s>0
置的弧长 s 作为质点位置
r
坐标. s 称自然坐标. s 可正
O
A

et
en
可负.
质点运动方程 s s(t)
自然坐标也可用矢量特征描述.
上页 下页 返回 结束
第二章 质点运动学
切向单位矢量 et 沿曲线切向,指向s>0方向. 法向单位矢量 en 沿曲线法向且指向曲线的凹侧.
a
an
at
O
(5)一般曲线运动
质点的曲线轨迹可视作由无限多个圆组合而成
a
at
an

dv dt
et
v2

en
——曲率圆半径
上页 下页 返回 结束
第二章 质点运动学
[例题1] 汽车在半径为200m的圆弧形公路上刹车，刹车
开始阶段的运动学方程为 s 20t 0.2t 3 (单位：m，s).
第二章 质点运动学
§2.6 自然坐标·切向和法向加速度
§2.6.1 自然坐标 §2.6.2 速度·法向和切向加速度
上页 下页 返回 结束
第二章 质点运动学
§2.6 自然坐标·切向和法向加速度
§2.6.1 自然坐标
若质点轨迹已知，质点的运动可分解为切向和法向.
自然坐标——将质点轨迹曲线作为一维坐标的轴线
2. 质点作圆周运动的切向加速度和法向加速度
经t 质点速度增量
Δv v'v
取 AD=AC
a

lim
Δv
Δv Δ1v Δ2v
t0 Δt


v'
B
v


A
O
lim Δ1v lim Δ2v
t0 Δt t0 Δt
(1)法向加速度
t0时，近似有 Δ1v v
上页 下页 返回 结束
第二章 质点运动学
(2)在落地点 v v0et
v v0
an g cos(45 )
R

v2 an

v02 g cos(45 )
902 9.8 2
m 1169m 2
上页 下页 返回 结束
第二章 质点运动学
[例题3]质点M在水平面内运动轨迹如图 ， t=0 时M在 O点，质点运动规律 s=30t+5t2 (m)，求t=2s时，质点M 的法向和切向加速度.
v
Dv
P
v'
Δ
2v
C
Δ1v
A
Δ1v

vΔ

v
AB R

v
vΔt R
上页 下页 返回 结束
法向加速度
第二章 质点运动学
an
lim Δ1v
Δt0 Δt
v2 R
an

v2 R
en
an反映速度方向变化的快慢 .
(2)角速率 定义
lim Δ
Δt0 Δt
炮弹运动的速度与加速度为
v
v0

cosi

(v0
sin

gt
)
j
a g gj
(1)在最高点 v y v0 sin gt 0
v v0 cos an g
R v2 an (v0 co2 m 413.3m
v0 g v02 g2t 2


arctan

lim
Δt 0
Δv Δt
et

dv dt
et
at反映速度大小的变化率
上页 下页 返回 结束
第二章 质点运动学
(4)总加速度
a
at
an

dv dt
et

v2 R
en
dv dt et


2
Ren
a an2 at2
tan an
v
at
上页 下页 返回 结束
[解]
(1)
x

v0t 1
y x2g

1 2
gt 2
y 2
v02
(2) vx v0 v y gt
第二章 质点运动学

O v0
x

an
at
y
g
v
v
2 x

v
2 y

v02 g2t 2
dv
g2t
at dt v02 g2t 2
an
g2 at2