大学物理切向加速和法向加速

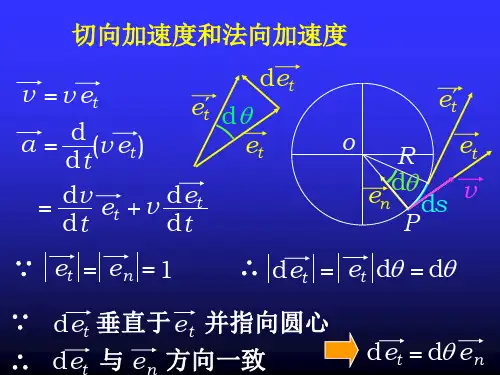
1-1.质点在Oxy 平面内运动，其运动方程为j t i t r )219(22-+=。

求：（1）质点的轨迹方程；（2）s .t 01=时的速度及切向和法向加速度。

1-2.一质点具有恒定加速度j i a 46+=，在0=t 时，其速度为零，位置矢量i r 100=。

求：（1）在任意时刻的速度和位置矢量；（2）质点在oxy 平面上的轨迹方程，并画出轨迹的示意图。

1-3. 一质点在半径为m .r 100=的圆周上运动，其角位置为342t +=θ。

（1）求在s .t 02=时质点的法向加速度和切向加速度。

（2）当切向加速度的大小恰等于总加速度大小的一半时，θ值为多少？（3）t 为多少时，法向加速度和切向加速度的值相等？题3解： (1)由于342t +=θ，则角速度212t dt d ==θω，在t = 2 s 时，法向加速度和切向加速度的数值分别为 222s 2t n s m 1030.2-=⋅⨯==ωr a22s t t s m 80.4d d -=⋅==t r a ω(2)当2t 2n t 212a a a a +==时，有2n 2t 3a a=，即 22212)24(3)r t (tr = s 29.0s 321==t此时刻的角位置为 rad.t 153423=+=θ (3)要使t n a a =，则有2212)24()t (r tr =s .t 550=3-1如图所示，在水平地面上，有一横截面2m 20.0=S 的直角弯管，管中有流速为1s m 0.3-⋅=v 的水通过，求弯管所受力的大小和方向。

解：在t ∆时间内，从管一端流入（或流出）水的质量为t vS m ∆=∆ρ,弯曲部分AB 的水的动量的增量则为()()A B A B v v t vS v v m p -∆=-∆=∆ρ依据动量定理p I ∆=，得到管壁对这部分水的平均冲力()A B v v I F -=∆=Sv t ρ从而可得水流对管壁作用力的大小为N 105.2232⨯-=-=-='Sv F F ρ作用力的方向则沿直角平分线指向弯管外侧。

大物切向加速度和法向加速度公式在我们探索物理世界的奇妙旅程中，大物切向加速度和法向加速度公式就像是两把神奇的钥匙，能帮助我们打开许多未知的大门。

咱先来说说切向加速度。

这切向加速度啊，简单来说，就是描述物体在运动轨迹切线方向上速度变化快慢的物理量。

它的公式是$a_{t} = \frac{dv}{dt}$，这里的$v$表示速度，$dt$表示时间的微小变化量。

给您举个例子吧，就说骑自行车。

您在平坦的道路上骑车，使劲儿蹬的时候，车子速度越来越快，这个速度增加的快慢程度，在物理上就可以用切向加速度来衡量。

比如说，您一开始以 5 米每秒的速度前进，然后在 5 秒钟内加速到了 10 米每秒。

那速度的变化量就是 10 - 5= 5 米每秒。

时间变化量是 5 秒。

所以切向加速度就是 5÷5 = 1 米每秒²。

这就意味着您骑车的速度每秒增加了 1 米。

再聊聊法向加速度。

法向加速度呢，是描述物体在运动轨迹法向方向上速度变化快慢的物理量。

它的公式是$a_{n} = \frac{v^{2}}{r}$，其中$v$是速度，$r$是运动轨迹的曲率半径。

还拿骑车举例，当您骑着车转弯的时候，您会感觉到有一种向外甩的力。

这个时候就有法向加速度在起作用啦。

比如说您以 8 米每秒的速度骑进一个半径为 10 米的弯道，那法向加速度就是 8²÷10 = 6.4 米每秒²。

这股力量会让您在转弯的时候紧紧握住车把，保持平衡。

在实际生活中，这两个加速度常常是同时存在的。

就像汽车在盘山公路上行驶，既沿着道路有速度的变化（切向加速度），又因为道路的弯曲而有向心的加速度（法向加速度）。

对于学习物理的同学们来说，理解这两个加速度公式可太重要啦。

在解题的时候，搞清楚物体的运动状态，准确判断是切向加速度在起主要作用，还是法向加速度更关键，或者是两者都要考虑，这是解题的关键步骤。

总之，大物中的切向加速度和法向加速度公式虽然看起来有点复杂，但只要我们结合实际生活中的例子去理解，就会发现它们其实就在我们身边，无时无刻不在影响着我们的生活和运动。

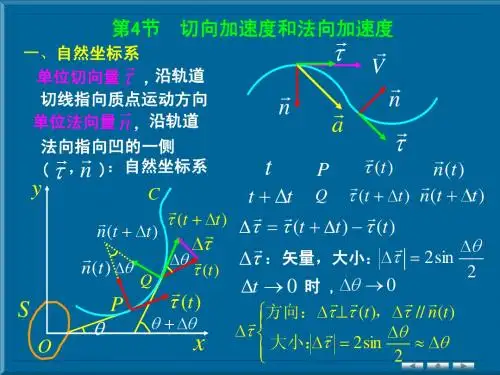
第4章 刚体的定轴转动 习题及答案1．刚体绕一定轴作匀变速转动，刚体上任一点是否有切向加速度？是否有法向加速度？切向和法向加速度的大小是否随时间变化？答：当刚体作匀变速转动时,角加速度β不变。

刚体上任一点都作匀变速圆周运动，因此该点速率在均匀变化，v l ω=，所以一定有切向加速度t a l β=，其大小不变。

又因该点速度的方向变化，所以一定有法向加速度2n a l ω=，由于角速度变化，所以法向加速度的大小也在变化。

2. 刚体绕定轴转动的转动定律和质点系的动量矩定理是什么关系？答：刚体是一个特殊的质点系，它应遵守质点系的动量矩定理，当刚体绕定轴Z 转动时，动量矩定理的形式为zz dL M dt=，z M 表示刚体对Z 轴的合外力矩，z L 表示刚体对Z 轴的动量矩。

()2z i i L m l I ωω==∑,其中()2i i I m l =∑，代表刚体对定轴的转动惯量，所以()z z dL d d M I I I dt dt dtωωβ====。

既 z M I β=。

所以刚体定轴转动的转动定律是质点系的动量矩定理在刚体绕定轴转动时的具体表现形式，及质点系的动量矩定理用于刚体时在刚体转轴方向的分量表达式。

3．两个半径相同的轮子，质量相同，但一个轮子的质量聚集在边缘附近，另一个轮子的质量分布比较均匀，试问：（1）如果它们的角动量相同，哪个轮子转得快？（2）如果它们的角速度相同，哪个轮子的角动量大？答：(1)由于L I ω=，而转动惯量与质量分布有关，半径、质量均相同的轮子，质量聚集在边缘附近的轮子的转动惯量大，故角速度小，转得慢，质量分布比较均匀的轮子转得快；（2）如果它们的角速度相同，则质量聚集在边缘附近的轮子角动量大。

4．一圆形台面可绕中心轴无摩擦地转动，有一玩具车相对台面由静止启动，绕轴作圆周运动，问平台如何运动？如小汽车突然刹车，此过程角动量是否守恒？动量是否守恒？能量是否守恒？答：玩具车相对台面由静止启动，绕轴作圆周运动时，平台将沿相反方向转动；小汽车突然刹车过程满足角动量守恒，而能量和动量均不守恒。

刚体复习重点（一）要点质点运动位置矢量(运动方程) r = r (t ) = x (t )i + y (t )j + z (t )k ，速度v = d r/d t = (d x /d t )i +(d y /d t )j + (d z /d t )k ，动量 P=m v加速度 a=d v/d t=(d v x /d t )i +(d v y /d t )j +(d v z /d t )k曲线运动切向加速度 a t = d v /d t ， 法向加速度 a n = v 2/r .圆周运动及刚体定轴转动的角量描述 θ=θ(t )， ω=d θ/d t ， β= d ω/d t =d 2θ/d t 2，角量与线量的关系 △l=r △θ， v=r ω (v= ω×r )，a t =r β, a n =r ω2力矩 M r F 转动惯量 2i i J r m =∆∑， 2d mJ r m =⎰ 转动定律 t d L M =M J α= 角动量： 质点p r L ⨯= 刚体L=J ω；角动量定理 ⎰tt 0d M =L -L 0角动量守恒 M=0时, L=恒量； 转动动能2k E J ω= (二) 试题一 选择题（每题3分）1．一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮，绳的两端分别悬有质量为m 1和m 2的物体(m 1＜m 2)，如图．绳与轮之间无相对滑动．若某时刻滑轮沿逆时针方向转动，则绳中的张力（答案：C ）(A) 处处相等． (B) 左边大于右边．(C) 右边大于左边． (D) 哪边大无法判断． 2．将细绳绕在一个具有水平光滑轴的飞轮边缘上，现在在绳端挂一质量为m 的重物，飞轮的角加速度为β．如果以拉力2mg 代替重物拉绳时，飞轮的角加速度将 （答案：C ）(A) 小于β． (B) 大于β，小于2 β． (C) 大于2 β． (D) 等于2 β．3. 均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图所示，今使棒从水平位置由静止开始自由下落，在棒摆动到竖立位置的过程中，下述说法哪一种是正确的？(A) 角速度从小到大，角加速度从大到小. (答案：A ）(B) 角速度从小到大，角加速度从小到大.(C) 角速度从大到小，角加速度从大到小.(D) 角速度从大到小，角加速度从小到大.4. 关于刚体对轴的转动惯量，下列说法中正确的是（答案：C ）(A) 只取决于刚体的质量，与质量的空间分布和轴的位置无关.(B) 取决于刚体的质量和质量的空间分布，与轴的位置无关.(C) 取决于刚体的质量，质量的空间分布和轴的位置.(D) 只取决于转轴的位置，与刚体的质量和质量的空间分布无关.5. 花样滑冰运动员绕通过自身的竖直轴转动，开始时两臂伸开，转动惯量为J 0，角速度为ω0．然后她将两臂收回，使转动惯量减少为J 0/3．这时她转动的角速度变为（答案：D ）(A) ω0/3． (B) ()3/1 ω0． (C) 3 ω0． (D) 3ω0．二、填空题1.（本题4分）一飞轮作匀减速运动，在5s 内角速度由40π rad/s 减少到10π rad/s ，则飞轮在这5s内总共转过了 圈，飞轮再经 的时间才能停止转动。

切向加速度和法向加速度在车辆行驶中的作用车辆行驶中的切向加速度和法向加速度作用分析车辆行驶中，切向加速度和法向加速度是两个重要的物理概念，它们对车辆的运动轨迹和行驶稳定性起着非常关键的作用。

本文将深入探讨切向加速度和法向加速度在车辆行驶中的作用，并分析其对车辆行驶的影响。

一、切向加速度的作用切向加速度是指车辆在行驶过程中速度方向的变化率，也可以理解为车辆在弯道行驶时的加速度。

切向加速度的作用主要有三个方面。

首先，切向加速度可以控制车辆在弯道行驶中的转向速度。

当车辆进入一个转弯道路时，为了保持行驶轨迹的稳定，司机需要施加足够的切向加速度，使车辆保持在预定的曲线上行驶。

若切向加速度不足，车辆容易偏离预定轨迹，甚至发生侧滑等危险情况。

其次，切向加速度可以增加车辆的抓地力。

在弯道行驶中，车辆受到的向心力会使车辆向外侧倾斜，这时切向加速度可以产生向内的力，抵消向心力的影响，使车辆保持在弯道上行驶。

合理的切向加速度能够有效提高车辆的抓地力，增强行驶稳定性。

再次，切向加速度对车辆的纵向动力学性能有重要影响。

通过控制切向加速度，司机可以灵活应对道路的变化和车辆的需求，实现加速、减速和保持速度的动作。

合理和精确地掌握切向加速度可以提高车辆的驾驶性能，如加速灵敏、平顺换挡等。

二、法向加速度的作用法向加速度是指车辆在行驶过程中速度大小的变化率，它与车辆行驶的方向垂直，也可称为纵向加速度。

法向加速度的作用主要体现在以下几个方面。

首先，法向加速度可以影响车辆的制动性能。

在紧急制动或缓慢停车时，司机需要控制刹车力的大小，使车辆实现平稳的停车动作。

法向加速度的大小和变化率将直接影响到车辆制动的平稳性和安全性。

其次，法向加速度对车辆的悬挂系统和轮胎磨损有一定的影响。

当车辆通过坑洼路面或颠簸路段时，会产生较大的法向加速度，导致车辆悬挂系统承受较大的冲击力，影响乘坐舒适性。

此外，法向加速度还会使轮胎产生较大的摩擦力，引起胎面磨损，影响轮胎寿命。