第三讲-切向加速度与法向加速度
- 格式:ppt
- 大小:1006.61 KB
- 文档页数:8



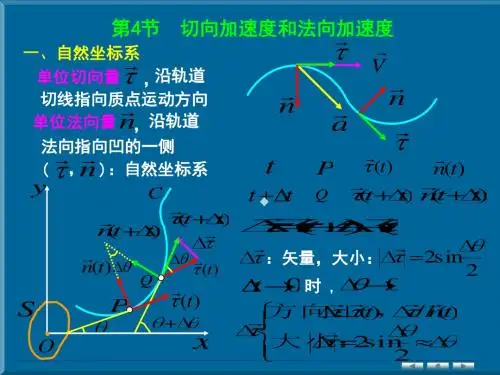
法向加速度和切向加速度的物理意义
法向加速度和切向加速度是描述物体运动状态的两个重要参数。
法向加速度是指物体在其运动轨迹的法线方向上的加速度,也就是垂直于物体的速度方向的加速度。
切向加速度是指物体在其运动轨迹的切线方向上的加速度,也就是平行于物体的速度方向的加速度。
在物理学中,法向加速度和切向加速度是描述物体运动状态的两个基本参数。
它们可以帮助我们更好地了解物体运动的特征和规律。
法向加速度和切向加速度的物理意义如下:
1. 法向加速度的物理意义
法向加速度是指物体在其运动轨迹的法线方向上的加速度。
它与速度的方向垂直,所以也称为径向加速度。
法向加速度可以帮助我们判断物体是否在向心运动,也可以帮助我们计算物体在曲线道路上运动时所需的力和能量。
例如,当一个车辆在曲线道路上行驶时,它会受到向心力的作用,这个向心力的大小与车辆的速度、质量以及曲率有关。
如果我们知道了车辆在曲线道路上行驶时的法向加速度,就可以通过公式 F = ma 来计算向心力的大小,从而更好地控制车辆的行驶。
2. 切向加速度的物理意义
切向加速度是指物体在其运动轨迹的切线方向上的加速度。
它与速度的方向平行,所以也称为切线加速度。
切向加速度可以帮助我们判断物体在水平方向上的运动特征,也可以帮助我们计算物体在曲线道路上的侧向力和侧向加速度。
例如,当一个车辆在曲线道路上行驶时,它会受到侧向力的作用,这个侧向力的大小与车辆的速度、质量以及曲率有关。
如果我们知道了车辆在曲线道路上行驶时的切向加速度,就可以通过公式 F = ma 来计算侧向力的大小,从而更好地控制车辆的行驶。

角加速度切向加速度和法向加速度关系角加速度、切向加速度和法向加速度是三个密切相关的物理量,在运动学和动力学中都有着重要的作用。
它们之间存在着一定的关系,下面我们来具体了解一下。
首先,角加速度是描述物体旋转状态的物理量,它表示单位时间内,物体旋转角速度的变化率。
在平面运动中,若物体绕固定点做匀速圆周运动,则其角加速度大小为零。
若物体绕固定点做变速圆周运动,则其角加速度大小为非零值,且方向始终与物体运动方向垂直,根据右手定则可知,角加速度方向遵循“向内加速”的方向规律。
其次,切向加速度是描述物体在圆周运动中速度变化的物理量,它表示单位时间内物体在圆周方向上速度的变化率。
在匀速圆周运动中,物体速度大小不变,因此其切向加速度大小为零。
而在非匀速圆周运动中,物体速度大小随时间变化,因此其切向加速度大小不为零,且方向始终沿着物体运动方向。
切向加速度的大小可以通过求导物体速度关于时间的变化率来计算。
最后,法向加速度是描述物体在圆周运动中方向变化的物理量,它表示单位时间内物体在圆周垂直方向上速度的变化率。
在匀速圆周运动中,物体速度方向始终沿着圆周切线方向,因此其法向加速度大小为零。
而在非匀速圆周运动中,物体速度方向发生变化,因此其法向加速度大小不为零,且方向垂直于切向加速度方向,向圆心方向。
法向加速度的大小可以通过求导物体速度关于时间的方向变化率来计算。
综上所述,角加速度、切向加速度和法向加速度三者之间的关系可以用以下公式表示:a = √(aT + aN)其中,a表示合加速度,aT表示切向加速度,aN表示法向加速度。
这个公式说明了,物体在圆周运动中所受到的合加速度大小等于切向加速度和法向加速度的平方和的开方。
同时,切向加速度和法向加速度方向也分别与合加速度方向垂直和水平。

切向加速度和法向加速度-资料类关键信息项:1、切向加速度的定义及相关概念名称:____________________________描述:____________________________2、法向加速度的定义及相关概念名称:____________________________描述:____________________________3、切向加速度和法向加速度的计算方法公式:____________________________适用条件:____________________________4、切向加速度和法向加速度的关系相互影响:____________________________关联因素:____________________________5、实际应用场景举例场景描述:____________________________作用分析:____________________________11 切向加速度的定义切向加速度是质点作曲线运动时所具有的沿轨道切线方向的加速度。
它描述了质点速度大小变化的快慢程度。
111 切向加速度的计算公式切向加速度的大小可以通过对速度大小对时间的导数来计算,即:$a_{t} =\frac{dv}{dt}$,其中$v$是速度大小,$t$是时间。
112 切向加速度的影响因素切向加速度的大小取决于作用在质点上的切向力以及质点的质量。
当切向力增大或质点质量减小时,切向加速度会增大,反之则减小。
12 法向加速度的定义法向加速度是质点作曲线运动时所具有的沿轨道法线方向(指向曲率中心)的加速度。
它反映了质点速度方向变化的快慢。
121 法向加速度的计算公式法向加速度的大小为:$a_{n} =\frac{v^2}{r}$,其中$v$是质点的速度大小,$r$是曲线运动轨迹的曲率半径。
122 法向加速度的特点法向加速度始终指向曲线的曲率中心,其大小与速度的平方成正比,与曲率半径成反比。


大物切向加速度和法向加速度公式在我们探索物理世界的奇妙旅程中,大物切向加速度和法向加速度公式就像是两把神奇的钥匙,能帮助我们打开许多未知的大门。
咱先来说说切向加速度。
这切向加速度啊,简单来说,就是描述物体在运动轨迹切线方向上速度变化快慢的物理量。
它的公式是$a_{t} = \frac{dv}{dt}$,这里的$v$表示速度,$dt$表示时间的微小变化量。
给您举个例子吧,就说骑自行车。
您在平坦的道路上骑车,使劲儿蹬的时候,车子速度越来越快,这个速度增加的快慢程度,在物理上就可以用切向加速度来衡量。
比如说,您一开始以 5 米每秒的速度前进,然后在 5 秒钟内加速到了 10 米每秒。
那速度的变化量就是 10 - 5= 5 米每秒。
时间变化量是 5 秒。
所以切向加速度就是 5÷5 = 1 米每秒²。
这就意味着您骑车的速度每秒增加了 1 米。
再聊聊法向加速度。
法向加速度呢,是描述物体在运动轨迹法向方向上速度变化快慢的物理量。
它的公式是$a_{n} = \frac{v^{2}}{r}$,其中$v$是速度,$r$是运动轨迹的曲率半径。
还拿骑车举例,当您骑着车转弯的时候,您会感觉到有一种向外甩的力。
这个时候就有法向加速度在起作用啦。
比如说您以 8 米每秒的速度骑进一个半径为 10 米的弯道,那法向加速度就是 8²÷10 = 6.4 米每秒²。
这股力量会让您在转弯的时候紧紧握住车把,保持平衡。
在实际生活中,这两个加速度常常是同时存在的。
就像汽车在盘山公路上行驶,既沿着道路有速度的变化(切向加速度),又因为道路的弯曲而有向心的加速度(法向加速度)。
对于学习物理的同学们来说,理解这两个加速度公式可太重要啦。
在解题的时候,搞清楚物体的运动状态,准确判断是切向加速度在起主要作用,还是法向加速度更关键,或者是两者都要考虑,这是解题的关键步骤。
总之,大物中的切向加速度和法向加速度公式虽然看起来有点复杂,但只要我们结合实际生活中的例子去理解,就会发现它们其实就在我们身边,无时无刻不在影响着我们的生活和运动。


如何通过切向加速度和法向加速度判断物体的运动加速度方向切向加速度和法向加速度是物体运动中的两个重要概念,通过它们的方向可以判断物体的运动加速度方向。
本文将探讨如何利用切向加速度和法向加速度来判断物体的运动加速度方向。
切向加速度是指物体在弯曲运动中的加速度,也可以理解为物体在曲线轨迹上的加速度。
在弯曲运动中,物体所受到的力可以分解为切向力和法向力两个分量。
切向力使物体在曲线轨迹上改变速度,法向力使物体向曲线轨迹的中心偏移。
根据牛顿第二定律,物体在弯曲运动中的切向加速度与物体所受切向力成正比,与物体的质量成反比。
法向加速度是指物体在曲线运动中的加速度,是物体在弯曲轨迹上向曲线外侧偏移的加速度。
在弯曲运动中,法向加速度与物体受到的法向力成正比,与物体的质量成反比。
法向力使物体向曲线轨迹的中心偏移,而法向加速度则表示物体沿曲线轨迹的加速度。
通过观察切向加速度和法向加速度的方向可以判断物体的运动加速度方向。
如果切向加速度的方向与物体的运动方向一致,表明物体的运动加速度与运动方向相同;如果切向加速度的方向与物体的运动方向相反,表明物体的运动加速度与运动方向相反。
同样,如果法向加速度的方向与物体的运动方向一致,表示物体的运动加速度与运动方向相同;如果法向加速度的方向与物体的运动方向相反,表示物体的运动加速度与运动方向相反。
例如,当一个物体在弯曲轨迹上做匀速圆周运动时,其速度大小不变,但由于方向不断改变,所以物体存在切向加速度。
这时切向加速度的方向与物体的速度方向相互垂直,指向曲线轨迹的中心。
而法向加速度的方向指向曲线轨迹的外侧,与速度方向相互垂直。
因此,在匀速圆周运动中,物体的运动加速度方向指向曲线轨迹的中心。
总结起来,通过切向加速度和法向加速度的方向可以判断物体的运动加速度方向。
切向加速度与运动方向一致表示运动加速度与方向相同,切向加速度与运动方向相反表示运动加速度与方向相反;法向加速度与运动方向一致表示运动加速度与方向相同,法向加速度与运动方向相反表示运动加速度与方向相反。

法向加速度和切向加速度的物理意义
法向加速度和切向加速度是描述物体运动状态的重要物理量。
法向加速度是垂直于物体运动方向的加速度,也被称为向心加速度。
它的物理意义是描述物体在弯曲运动过程中,受到向心力作用的加速度大小。
例如,当汽车在转弯时,车辆的向心加速度越大,车体所受到的离心力也越大,这会影响到行驶的稳定性和安全性。
切向加速度是沿着物体运动轨迹方向的加速度。
它的物理意义是描述物体在直线运动中,受到的加速度大小。
例如,当汽车在直线行驶时,车辆的切向加速度决定了车速的变化情况。
如果切向加速度为正,车速将增加;如果切向加速度为负,车速将减少。
在实际运动中,物体的运动状态通常是由法向加速度和切向加速度共同作用所决定的。
例如,当物体在弯曲的运动过程中,需要同时考虑向心力的作用和物体自身的惯性作用。
另外,法向加速度和切向加速度的大小和方向也会影响到物体的动能和势能的变化,从而影响到动力学过程的发展。
因此,了解法向加速度和切向加速度的物理意义,对于研究物体运动状态和动力学过程具有重要的意义。
- 1 -。
法向加速度和切向加速度的公式推导在我们探索物理世界的奇妙旅程中,加速度这个概念可是相当重要的哟!今天咱们就来好好唠唠法向加速度和切向加速度的公式推导。
咱们先来说说法向加速度。
想象一下,你骑着自行车在路上飞驰,车轮不停地转动。
当车轮在做圆周运动时,就会产生法向加速度。
那这法向加速度是咋来的呢?假设一个质点在平面内做圆周运动,它的位置可以用极坐标表示为$(r, \theta)$。
那它的速度$v$可以分解为沿半径方向的速度$v_r$和沿圆周切线方向的速度$v_{\theta}$。
咱们重点关注沿圆周切线方向的速度$v_{\theta}$,它的大小是$v_{\theta} = r\omega$,其中$\omega$是角速度。
而角速度$\omega$的变化率就是角加速度$\alpha$。
现在,咱们来推导法向加速度$a_n$的公式。
因为速度的变化量$\Delta v$与圆周运动的半径垂直,所以法向加速度$a_n$就等于速度的变化量$\Delta v$除以时间$\Delta t$。
当时间$\Delta t$趋近于 0 时,速度的变化量$\Delta v$就趋近于$v\omega$,所以法向加速度$a_n = v\omega$。
又因为$v = r\omega$,所以法向加速度$a_n = r\omega^2$。
再来说说切向加速度。
还拿骑自行车举例子,当你用力蹬车,让车速变快或者变慢的时候,这产生的加速度就是切向加速度。
假如一个质点在曲线运动中,它的路程$s$与时间$t$的关系是$s =s(t)$。
那么它的速度$v$就是路程对时间的导数,$v = \frac{ds}{dt}$。
切向加速度$a_t$就是速度对时间的导数,$a_t = \frac{dv}{dt}$。
给大家讲个我自己的事儿吧。
有一次我在公园里散步,看到一个小朋友在玩轮滑。
他沿着一个圆形的花坛边缘滑,滑得还挺快。
我就在旁边观察,心里想着他的运动轨迹,不就是咱们今天说的这种圆周运动嘛。
法向加速度和切向加速度的物理意义
法向加速度和切向加速度是描述物体运动状态的重要物理量。
法向加速度是垂直于物体运动方向的加速度,切向加速度则是沿物体运动方向的加速度。
法向加速度的物理意义是描述物体在运动过程中,沿着曲线运动时,速度大小和方向随时在改变,因而需要进行向心力的修正,使得物体沿着曲线的路径运动。
换句话说,法向加速度是物体在曲线运动中的向心加速度,它的大小与物体的质量、速度和曲率有关。
切向加速度则是描述物体在运动过程中,沿着曲线运动时,速度的大小随时间改变的情况。
换句话说,它是物体在曲线运动中沿着曲线方向的加速度,它的大小与物体的速度和曲率有关。
在自然界中,曲线运动的例子非常多,比如说行星绕太阳的运动、自行车在转弯时的运动等等。
因此,了解和掌握法向加速度和切向加速度的物理意义对于理解物体运动的规律和现象是非常重要的。
- 1 -。
切向加速度和法向加速度公式在物理学中,我们经常会遇到切向加速度和法向加速度这两个概念。
切向加速度是描述物体在曲线轨迹上运动时,速度方向的变化率;而法向加速度则是描述物体在曲线轨迹上运动时,速度大小的变化率。
本文将详细介绍切向加速度和法向加速度的公式及其应用。
我们来看看切向加速度的公式。
在一维直线运动中,物体的加速度可以简单地表示为速度的变化率,即 a = Δv/Δt。
然而,当物体在曲线轨迹上运动时,速度的变化不仅与时间有关,还与速度的方向有关。
因此,我们需要引入切向加速度来描述速度的变化率。
切向加速度的公式可以表示为a_t = dv/dt,其中a_t表示切向加速度,v表示速度,t表示时间。
这个公式可以理解为切向加速度等于速度对时间的导数。
切向加速度的方向与速度的方向相同,大小则取决于速度变化的快慢。
接下来,我们来介绍法向加速度的公式。
法向加速度描述的是物体在曲线轨迹上运动时,速度大小的变化率。
当物体在曲线上运动时,其速度方向会随着曲率的变化而改变,这就引入了法向加速度的概念。
法向加速度的公式可以表示为a_n = v^2/ρ,其中a_n表示法向加速度,v表示速度,ρ表示曲率半径。
这个公式可以理解为法向加速度等于速度的平方除以曲率半径。
法向加速度的方向与曲率半径的方向相同,大小则取决于速度的平方和曲率半径的比值。
切向加速度和法向加速度经常同时存在,描述了物体在曲线轨迹上运动时速度的变化情况。
它们的合成加速度可以表示为 a = √(a_t^2 + a_n^2),即合成加速度等于切向加速度的平方和法向加速度的平方的平方根。
切向加速度和法向加速度的应用非常广泛。
在机械工程中,当物体在曲线轨迹上运动时,需要考虑切向加速度和法向加速度对物体的影响。
例如,在车辆转弯时,切向加速度和法向加速度会影响车辆的稳定性和操控性能。
在空气动力学中,切向加速度和法向加速度会影响飞机的飞行状态和稳定性。
在物理学中,切向加速度和法向加速度是描述质点在曲线轨迹上运动时的重要概念。