切向加速与法向加速

圆周运动法向加速度和切向加速度的公式文档下载说明Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document 圆周运动法向加速度和切向加速度的公式can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!圆周运动是物体在绕圆周运动过程中所具有的加速度的运动。

在圆周运动中，物体除了沿着圆周方向的线速度外，还具有沿切线方向和法线方向的加速度。

其中，沿切线方向的加速度称为切向加速度，沿法线方向的加速度称为法向加速度。

1. 切向加速度的公式。

在圆周运动中，物体的速度方向会不断改变，因此会具有具有一个切向加速度。

切向加速度的大小等于速度的平方与弧长的乘积除以半径的平方，即。

科研探索
在物理学、天文学、生物学等科研领域，切向加速度和法向加速度的应用对于探索物体运动规律和现象 具有重要作用，能够促进科学研究的深入开展和创新。
THANKS FOR WATCHING
感谢您的观看
曲线运动中的切向加速度
在曲线运动中，切向加速度等于物体速率对时间 的变化率，即$a_{t} = frac{dv}{dt}$。
3
匀速圆周运动中的切向加速度
在匀速圆周运动中，切向加速度的大小为$a_{t} = omega^{2}r$，方向始终指向圆心。
切向加速度在现实生活中的应用
车辆转弯
汽车在转弯时，由于离心力作用， 车轮与地面之间产生侧向摩擦力，
工程设计和优化
在机械、航空、交通等领域，切向加速度和法向加速度的应用对于工程设计和优化至关重要，能够帮助工程师更好地 分析物体的运动特性和受力情况，提高设计质量和安全性。
体育科技
在体育领域，切向加速度和法向加速度的应用对于运动分析和技术优化具有重要意义，能够帮助教练和运动员更好地 理解运动过程中的技术细节和改进方向。
使汽车产生切向加速度，影响车 辆行驶稳定性。
旋转机械
旋转机械在运转过程中，由于摩擦 力或外部扰动作用，会产生切向加 速度，影响机械的正常运转。
投掷运动
在投掷运动中，如标枪、铁饼等， 运动员通过施加切向力使器械产生 切向加速度，从而影响器械飞行的 轨迹和距离。
03 法向加速度
法向加速度的概念
法向加速度是描述物体在圆周运动或 曲线运动中速度方向变化快慢的物理 量。
在不同运动状态下的表现
01
02
03
匀速圆周运动
切向加速度为零，法向加 速度不为零，物体做匀速 圆周运动。

在圆周运动中，法向加速度的大小与 半径和线速度的平方成正比。
法向加速度的计算公式
在圆周运动中，法向加速度的大小可以通过公式an = v²/r计算，其中an表示法 向加速度，v表示线速度，r表示半径。
对于一般的曲线运动，法向加速度的大小可以通过公式an = dv/dt计算，其中an 表示法向加速度，dv/dt表示速度的变化率。
03 切向加速度与法向加速 度的关系
圆周运动中的切向加速度与法向加速度
切向加速度
描述物体在圆周运动中速度大小的变化，即线速度的变化率。
法向加速度
描述物体在圆周运动中速度方向的改变，即角速度的变化率。
曲线运动中的切向加速度与法向加速度
切向加速度
描述物体在曲线运动中速度大小的变 化。
法向加速度
描述物体在曲线运动中速度方向的改 变。
在航天器进行轨道变化时，需要产生法向加速度来改变其轨道半径或轨道倾角。这可以通过调整发动 机推力和飞行姿态来实现。
切向加速度与法向加速度在日常生活中的应用
游乐设施
游乐场中的过山车、旋转木马等设施利用了切向加速度和法向加速度的原理，使游客能 够体验刺激和乐趣。
体育竞技
在赛车、自行车等竞技项目中，运动员通过控制切向加速度和法向加速度来提高速度、 改变运动方向或完成特定动作。
切向加速度和法向加速度 课件
• 切向加速度与法向加速度的关
目
录
• 切向加速度和法向加速度的应
• 切向加速度和法向加速度的实
01 切向加速度
切向加速度的定 义
切向加速度
描述物体在圆周运动或曲线运动 中，沿运动轨迹切线方向的加速度。
公式表示
at = d^2r/dt^2 ，其中 r 为物体 在曲线上的位置矢量，t为时间。

r τ (t)
τ
r
θ
θ + θ
x
r τ r θ ： 大小 τ = 2sin 2 ≈ θ
dτ dτ dθ dτ dθ ds dτ r ds = ρ ds =V = = , =n , dθ , dt dt dθ dt dθ ds dt dθ
r τ ≈ θ n r r r dτ r τ θ n r lim θ →0, θlim θ = θ →0 θ = n dθ = n →0
α
r a
an
dV 2 V 2 2 2 a = at2 + an = ( ) + ( ) , tgα = an / at dt ρ
讨论：（1 直线运动， 讨论：（1）直线运动，ρ = ∞, an = 0 ：（ dV V2 a = 0, an = 匀速率圆周运动， （2）匀速率圆周运动， t = ：向心加速度 R dt 一般曲线运动及变速率圆周运动， （3）一般曲线运动及变速率圆周运动，at ≠ 0, an ≠ 0 V2 V2 （4） an = ρ= ：计算曲率半径
θ = 63.4o
第6节 节
圆周运动的角量表示
角坐标， s = Rθ θ ：角坐标，rad θ = θ (t) s = s(t)
y
r P r s θ A R O
V = ωR,
dω d 2θ ：角加速度， 角加速度， rad / s2 β= = 2 dt dt V 2 ω2 R2 = = ω2 R at = Rβ, an = R R
第5 节
相对运动
P
r r
S
O
静系
r r0
S′
O′
动系
r r′
r r r r = r ′ + r0 r r r dr dr ′ dr0 = + dt d = r′ + r0

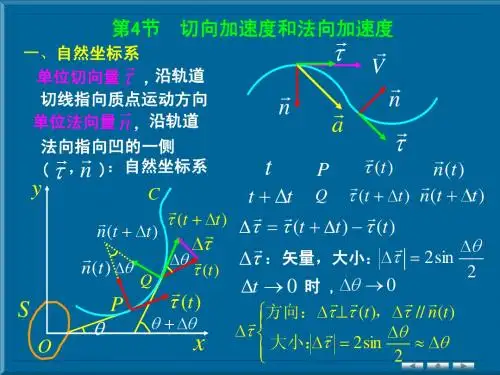
切向加速度和法向加速度
法向加速度：数值上等于速度v的平方除曲率半径r，或角速度ω的平方与半径r的乘积。

法向加速度的计算公式：an=ω^2r=v^2/r。

切向加速度：其值为线速度对时间的变化率。

切向加速度的计算公式：at=dv/dt。

切向加速度公式 at=dv/dt
法向加速度公式 an=v^2/r
切向加速度和法向加速度的区别：
1、切向加速度，改变的是速率的大小。

2、法向加速度，不改变速度的大小，只改变速度的方向。

3、切向加速度是质点作曲线运动时所具有的沿轨道切线方向的加速度。

而法向加速度是质点作曲线运动时，所具有的沿轨道法线方向的加速度。

匀变速圆周运动切向加速度和法向加速度匀变速圆周运动切向加速度和法向加速度是圆周运动中的两种
重要物理量。

切向加速度是指物体在圆周运动中速度方向的变化率，大小等于速度的变化率。

法向加速度是指物体在圆周运动中与圆心连线的方向上的加速度，大小等于速度的平方除以半径，与速度方向垂直。

这两种加速度的方向分别沿切线和法线方向，组成了物体在圆周运动中的总加速度。

在匀变速圆周运动中，切向加速度和法向加速度的大小和方向会随着时间而变化，但它们的大小是常数乘以速度的平方除以半径。

圆周运动中的切向加速度和法向加速度对于理解天体运动、机械运动等领域有着重要的应用。

- 1 -。

切向加速度和法向加速度求合加速度切向加速度和法向加速度是研究物体运动过程中重要的概念。

切向加速度是指物体运动轨迹上速度的变化率，而法向加速度是指物体运动轨迹的方向的变化率。

合加速度则是切向加速度和法向加速度的矢量合成。

首先，我们来看看切向加速度。

切向加速度描述了物体在沿着运动轨迹的方向上速度变化的快慢。

它的计算公式为：at = dv/dt其中，at表示切向加速度，dv表示速度的变化量，dt表示时间的变化量。

要理解切向加速度的概念，我们可以举一个例子。

假设你正驾驶一辆汽车在直线上行驶，车速不断增加。

在这种情况下，你会感受到一种向前的加速度，这就是切向加速度。

如果车速减小，则会感受到向后的切向加速度。

接下来，我们来看看法向加速度。

法向加速度描述了物体运动轨迹的方向变化的快慢。

它的计算公式为：an = v^2 / r其中，an表示法向加速度，v表示速度的大小，r表示运动轨迹的曲率半径。

为了更好地理解法向加速度的概念，我们可以再次举一个例子。

假设你正驾驶一辆汽车在一个弯道上行驶。

当你进入弯道时，你会感受到一个向内的加速度。

这是因为在弯道上行驶时，速度的方向会发生改变，因而产生了一个指向轨迹中心的法向加速度。

现在，我们来讨论合加速度。

合加速度是切向加速度和法向加速度的矢量合成。

它描述了物体在运动轨迹上由于速度大小和方向的改变而产生的综合效果。

合加速度的计算公式为：a = √(at² + an²)其中，a表示合加速度，at表示切向加速度，an表示法向加速度。

要理解合加速度的概念，我们可以回到前面的汽车驾驶的例子。

当你驾驶汽车在直线上行驶时，合加速度就等于切向加速度，在这种情况下，合加速度的方向和切向加速度的方向是一致的。

而在弯道上行驶时，合加速度的方向则既包括切向加速度的方向，也包括法向加速度的方向。

这是因为在弯道上行驶时，速度的大小和方向都在改变，所以合加速度的方向是一个合成的结果。

最后，我们来总结一下切向加速度和法向加速度求合加速度的过程。

角加速度切向加速度和法向加速度关系角加速度、切向加速度和法向加速度是三个密切相关的物理量，在运动学和动力学中都有着重要的作用。

它们之间存在着一定的关系，下面我们来具体了解一下。

首先，角加速度是描述物体旋转状态的物理量，它表示单位时间内，物体旋转角速度的变化率。

在平面运动中，若物体绕固定点做匀速圆周运动，则其角加速度大小为零。

若物体绕固定点做变速圆周运动，则其角加速度大小为非零值，且方向始终与物体运动方向垂直，根据右手定则可知，角加速度方向遵循“向内加速”的方向规律。

其次，切向加速度是描述物体在圆周运动中速度变化的物理量，它表示单位时间内物体在圆周方向上速度的变化率。

在匀速圆周运动中，物体速度大小不变，因此其切向加速度大小为零。

而在非匀速圆周运动中，物体速度大小随时间变化，因此其切向加速度大小不为零，且方向始终沿着物体运动方向。

切向加速度的大小可以通过求导物体速度关于时间的变化率来计算。

最后，法向加速度是描述物体在圆周运动中方向变化的物理量，它表示单位时间内物体在圆周垂直方向上速度的变化率。

在匀速圆周运动中，物体速度方向始终沿着圆周切线方向，因此其法向加速度大小为零。

而在非匀速圆周运动中，物体速度方向发生变化，因此其法向加速度大小不为零，且方向垂直于切向加速度方向，向圆心方向。

法向加速度的大小可以通过求导物体速度关于时间的方向变化率来计算。

综上所述，角加速度、切向加速度和法向加速度三者之间的关系可以用以下公式表示：a = √(aT + aN)其中，a表示合加速度，aT表示切向加速度，aN表示法向加速度。

这个公式说明了，物体在圆周运动中所受到的合加速度大小等于切向加速度和法向加速度的平方和的开方。

同时，切向加速度和法向加速度方向也分别与合加速度方向垂直和水平。

切向加速度和法向加速度－资料类关键信息项：1、切向加速度的定义及相关概念名称：＿___________________________描述：＿___________________________2、法向加速度的定义及相关概念名称：＿___________________________描述：＿___________________________3、切向加速度和法向加速度的计算方法公式：＿___________________________适用条件：＿___________________________4、切向加速度和法向加速度的关系相互影响：＿___________________________关联因素：＿___________________________5、实际应用场景举例场景描述：＿___________________________作用分析：＿___________________________11 切向加速度的定义切向加速度是质点作曲线运动时所具有的沿轨道切线方向的加速度。

它描述了质点速度大小变化的快慢程度。

111 切向加速度的计算公式切向加速度的大小可以通过对速度大小对时间的导数来计算，即：＄a_{t} ＝＼frac{dv}｛dt}＄，其中$v$是速度大小，＄t$是时间。

112 切向加速度的影响因素切向加速度的大小取决于作用在质点上的切向力以及质点的质量。

当切向力增大或质点质量减小时，切向加速度会增大，反之则减小。

12 法向加速度的定义法向加速度是质点作曲线运动时所具有的沿轨道法线方向（指向曲率中心）的加速度。

它反映了质点速度方向变化的快慢。

121 法向加速度的计算公式法向加速度的大小为：＄a_{n} ＝＼frac{v^2}｛r}＄，其中$v$是质点的速度大小，＄r$是曲线运动轨迹的曲率半径。

122 法向加速度的特点法向加速度始终指向曲线的曲率中心，其大小与速度的平方成正比，与曲率半径成反比。

切向加速度和法向加速度的物理意义
切向加速度和法向加速度是描述物体在曲线运动中发生加速度的两个重要概念。

切向加速度是物体在弯曲的曲线运动中，沿着曲线方向产生的加速度。

当物体在转弯时速度方向发生改变，因此它需要一个额外的加速度来改变方向，这就是切向加速度。

切向加速度的大小与曲率半径和物体的速度有关系。

法向加速度是物体在曲线运动中，垂直于切线方向的加速度。

当物体转向时，它会随着曲线半径的改变而改变速度，这就需要一个额外的加速度来改变速度大小，这就是法向加速度。

法向加速度的大小与物体速度的平方和曲率有关系。

综上所述，切向加速度和法向加速度描述了物体在曲线运动中的加速度情况，它们分别决定了物体的速度方向和大小的变化。

V 10 m /s
雨滴对车的速度为相对速度
V V
根据 V V V V V ,V 0 0
2 2 0
V0 V V V 22 . 4 m / s tg 2 V
63 .4
第 6节
圆周运动的角量表示
y
P r s Ax R O
sR ：角坐标，rad (t) s s(t)
V R ,
d d2 2 ：角加速度， rad / s 2 dt dt 2 2 2 V R 2 R at R , a n R R
ds d d V ( R ) R dt dt dt d ：角速度， rad /s dt 2 dV d d a R R 2 t dt dt dt
d V n dt
二、切向加速度和法向加速度

ds d ds V n , d , dt d

a a a n t n
dV d d dV dV V 2 a (V ) V n dt dt dt dt dt
a a a 0：绝对加速度=相对加速度+牵连加速度 如果 S 系相对于 S系作匀速直线运动，则 a a ,a 0 0
dV0 a0 ：O 点相对于 O 点的加速度（牵连加速度） dt
dt dt dt dV a ：质点在 S 系中的加速度（绝对加速度） dt dV a ：质点在 S 系中的加速度（相对加速度） dt
求： t= 2（分）， a , a t , a n
k =20/180=1/9，
V t 9
速率均匀增加，t = 3（分），V = 20m/s

ቤተ መጻሕፍቲ ባይዱ
—— 质点运动学 ——
伽利略变换、 伽利略变换、绝对时空理论
二船都以2m/s 3、在相对地面静止的坐标系内，A、B二船都以 在相对地面静止的坐标系内， 二船都以 的速率匀速行驶， 船沿 轴正向， 船沿 轴正向， 船沿x轴正向 船沿y轴正向 的速率匀速行驶，A船沿 轴正向， B船沿 轴正向， 今在A船上设置与地面坐标系方向相同的坐标系， 今在 船上设置与地面坐标系方向相同的坐标系，那 船上设置与地面坐标系方向相同的坐标系 么在A船上的坐标系中 船上的坐标系中， 船的速度为 么在 船上的坐标系中，B船的速度为 。 4、一飞机相对空气的速度大小为200km/h，风速为 一飞机相对空气的速度大小为 ， 56km/h，方向从西向东，地面雷达测得飞机的速率为 ，方向从西向东， 192km/h，则飞机相对地面运动的方向为 ， 。
o O′ z x z′ z
x
t′ = t
∗
z′ = z
—— 质点运动学 —— 伽利略变换、 伽利略变换、绝对时空理论
x′ = x − υt y′ = y
轴方向上。 设两参考系间的相对运动只发生在 x 轴方向上。 S系 S ′系 事件A 事件A ( x 1 , t 1 ) ′ ′ ( x1 , t1 ) 事件B 事件B ( x 2 , t 2 ) ′ ( x′ , t2 ) 2
1– 4
如何度量曲线弯曲程度？ 如何度量曲线弯曲程度？ P∆s P′
∆θ
ρ
ρ
曲率圆
∆θ dθ = 曲率： 曲率： k = lim ∆s→0 ∆ s ds ds 1 = 曲率半径： 曲率半径： ρ = dθ k
—— 质点运动学 —— 切向加速度、 切向加速度、法向加速度
v τ ( t + dt )

在实际问题中的应用选择
车辆行驶
在车辆行驶过程中，由于摩擦力和空气阻力的作用，车辆会受到切向加速度的影响，导致 速度的变化；而转弯时，车辆还会受到法向加速度的作用，改变运动方向。Байду номын сангаас
航天器轨道
航天器在绕地球运行时，受到地球引力的作用产生法向加速度，使得航天器沿着预定轨道 运行；同时，航天器在切线方向上也会受到其他力的作用，如太阳辐射压和大气阻力等， 这些力产生的切向加速度会影响航天器的速度和轨道半径。
实验步骤与操作
准备实验器材
滑轮、细绳、重物、测量尺、计时器等 。
VS
搭建实验装置
将滑轮固定在实验台上，细绳一端系住重 物，另一端跨过滑轮并可调节长度。
实验步骤与操作
实验操作 1. 调整细绳长度，使重物做近似圆周运动。
2. 记录重物运动的速度和时间，通过测量尺测量轨道半径。
实验步骤与操作
3. 改变重物运动的速度，重复实验。
思考三
如何理解切向加速度和法 向加速度在描述物体运动 状态中的作用？
THANKS
感谢观看
详细描述
在卫星轨道计算中，需要根据切向加速度来计算卫星的速度 和轨道半径；在曲线运动分析中，切向加速度用于描述物体 在曲线运动中的速度变化。
02
法向加速度
定义与公式
定义
法向加速度是描述速度矢量方向改变 的快慢程度的加速度，通常表示为an。
公式
an=v^2/r，其中v是速度大小，r是运 动物体到圆心的距离。
在不同运动形式下的表现
匀速圆周运动
自由落体运动
在匀速圆周运动中，切向加速度为零， 法向加速度等于向心加速度，方向始 终指向圆心。
自由落体运动中，物体只受到重力的 作用，切向加速度为零，法向加速度 等于重力加速度，方向始终竖直向下。

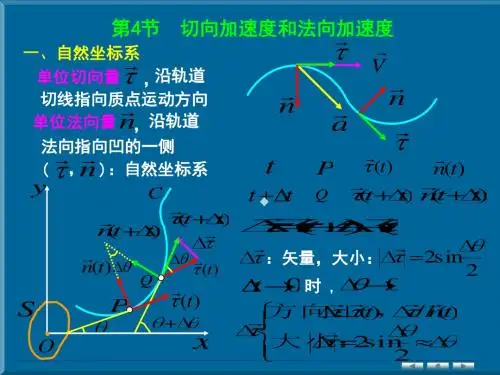
如何通过切向加速度和法向加速度判断物体的运动加速度方向切向加速度和法向加速度是物体运动中的两个重要概念，通过它们的方向可以判断物体的运动加速度方向。

本文将探讨如何利用切向加速度和法向加速度来判断物体的运动加速度方向。

切向加速度是指物体在弯曲运动中的加速度，也可以理解为物体在曲线轨迹上的加速度。

在弯曲运动中，物体所受到的力可以分解为切向力和法向力两个分量。

切向力使物体在曲线轨迹上改变速度，法向力使物体向曲线轨迹的中心偏移。

根据牛顿第二定律，物体在弯曲运动中的切向加速度与物体所受切向力成正比，与物体的质量成反比。

法向加速度是指物体在曲线运动中的加速度，是物体在弯曲轨迹上向曲线外侧偏移的加速度。

在弯曲运动中，法向加速度与物体受到的法向力成正比，与物体的质量成反比。

法向力使物体向曲线轨迹的中心偏移，而法向加速度则表示物体沿曲线轨迹的加速度。

通过观察切向加速度和法向加速度的方向可以判断物体的运动加速度方向。

如果切向加速度的方向与物体的运动方向一致，表明物体的运动加速度与运动方向相同；如果切向加速度的方向与物体的运动方向相反，表明物体的运动加速度与运动方向相反。

同样，如果法向加速度的方向与物体的运动方向一致，表示物体的运动加速度与运动方向相同；如果法向加速度的方向与物体的运动方向相反，表示物体的运动加速度与运动方向相反。

例如，当一个物体在弯曲轨迹上做匀速圆周运动时，其速度大小不变，但由于方向不断改变，所以物体存在切向加速度。

这时切向加速度的方向与物体的速度方向相互垂直，指向曲线轨迹的中心。

而法向加速度的方向指向曲线轨迹的外侧，与速度方向相互垂直。

因此，在匀速圆周运动中，物体的运动加速度方向指向曲线轨迹的中心。

总结起来，通过切向加速度和法向加速度的方向可以判断物体的运动加速度方向。

切向加速度与运动方向一致表示运动加速度与方向相同，切向加速度与运动方向相反表示运动加速度与方向相反；法向加速度与运动方向一致表示运动加速度与方向相同，法向加速度与运动方向相反表示运动加速度与方向相反。

角加速度切向加速度和法向加速度关系角加速度、切向加速度和法向加速度是描述物体运动状态的重要物理量，它们之间存在着密切的关系。

具体来说，角加速度是描述物体在固定轴上转动运动状态的物理量，切向加速度则是描述物体在曲线运动状态下沿曲线方向所受加速度的物理量，而法向加速度则是描述物体在曲线运动状态下垂直于曲线方向所受加速度的物理量。

同时，角加速度、切向加速度和法向加速度之间又存在着一系列的关系，这些关系是在物理学中有着重要应用价值的。

首先，角加速度与切向加速度之间存在着以下的关系：在物体在固定轴上转动的运动状态下，它的角加速度大小与物体所受的切向加速度大小之间存在着线性关系，即角加速度越大，物体所受的切向加速度也就越大。

具体来说，对于物体在固定轴上转动的运动状态而言，其角加速度的大小等于物体所受的切向加速度大小除以物体所在半径的大小，即α= a_t/r。

这个公式不仅可以用来计算固定轴上的物体所受的切向加速度大小，还可以用来计算物体所受的合力。

其次，切向加速度与法向加速度之间也存在着密切的关系：在物体进行曲线运动的状态下，它所受的切向加速度和法向加速度之间是相互依赖的。

具体表现为，在物体进行曲线运动的状态下，它的切向加速度大小是通过将物体在曲线上所受的合力分解为切向力和法向力的大小之后所得出的，即a_t=Ft/m，而物体所受的法向加速度大小则可以用物体所受的法向力大小除以物体的质量得出，即a_n=Fn/m。

最后，角加速度、切向加速度和法向加速度之间的关系还可以用来推导出物体在曲线运动状态下所受的合力大小和方向。

具体来说，对于物体在曲线运动状态下，如果我们知道了它所受的切向力大小和法向力大小，那么就可以分别计算出物体所受的切向加速度大小和法向加速度大小，然后再将这两个加速度向量合成为一个合加速度向量，即可得出物体所受的合力的大小和方向。

综上所述，角加速度、切向加速度和法向加速度之间存在着密切的关系，它们之间的相互依存关系在物理学中有着重要的应用价值。

2 2
结束
返回
圆周运动及其描述
一、切向加速度和法向加速度
2 v d v a= et + en = at + a n R dt
en
o an
a

P
et at
v d 切向加速度 at = et dt 法向加速度 a n = v e n R
2
v d at = dt v an = R
2
结束
返回
a = at + a n = at = arc tg an
t +Δ t B t A Δ θ o
..
θ
2. 角速度
平均角速度 瞬时角速度
x
ω ω
Δθ =Δ dt (rad.s-1)
结束
返回
3. 角加速度 Δ ω 平均角加速度 = Δt
d d ω ω θ Δ lim 瞬时角加速度 = = dt = dt 2 t Δ Δt 0
结束
返回
匀速圆周运动的运动方程
θ =θ 0+ ω 0t
匀变速圆周运动的运动方程
1 ω 0t + 0+ 2
θ =θ ω =ω 0 + t
t
2
x ~θ
v ~ω a~
2 ω 2= ω 0 ( θ0) + 2 θ
结束
返回
4. 线量和角量的关系 Δ s = RΔ θ
Δθ
R
Δs
θ = Rω lim Δ s = lim RΔ Δt Δt 0Δ t Δt 0
(v0 b t ) a = a t + an = ( b ) + R 2 an v b t ( ) 0 = arc tg arc tg = at Rb

匀加速圆周运动切向加速度和法向加速度匀加速圆周运动是物体在做圆周运动时线速度变化的过程。

在匀加速圆周运动中，物体运动的轨迹是一个圆。

而在圆周运动中，物体所受的加速度可以分解为切向加速度和法向加速度两个分量。

首先，我们来介绍切向加速度。

切向加速度是物体在圆周运动中沿切线方向的加速度。

在匀加速圆周运动中，物体的切向加速度的大小可以通过下面的公式计算：a_t = R * α其中，a_t表示切向加速度，R表示物体所处圆周运动的半径，α表示物体的角加速度。

从上面的公式可以看出，切向加速度的大小与半径和角加速度的乘积成正比。

接下来，我们来介绍法向加速度。

法向加速度是物体在圆周运动中指向圆心的加速度。

在匀加速圆周运动中，物体的法向加速度的大小可以通过下面的公式计算：a_n = v^2 / R其中，a_n表示法向加速度，v表示物体的线速度，R表示物体所处圆周运动的半径。

从上面的公式可以看出，法向加速度的大小与线速度的平方与半径的比值成正比。

需要注意的是，在匀加速圆周运动中，切向加速度和法向加速度是相互独立的，它们分别负责改变物体在切线方向和法向的运动状态。

匀加速圆周运动中的切向加速度和法向加速度对物体的运动具有重要影响。

切向加速度决定了物体的速度变化率，它使得物体在沿切线方向上不断加速或减速。

而法向加速度决定了物体的轨迹曲率变化率，它使得物体在做圆周运动时具有一个向心力。

在匀加速圆周运动中，物体所受的合加速度可以通过向量合成来得到。

合加速度的大小等于切向加速度和法向加速度两个分量的矢量和的模。

方向则与切向加速度和法向加速度两个分量的矢量和的方向相同。

总结起来，匀加速圆周运动中的切向加速度和法向加速度分别负责改变物体在切线方向和法向的运动状态，它们的大小与物体的运动状态以及圆周运动的半径有关。

了解切向加速度和法向加速度对于理解物体在匀加速圆周运动中的运动规律是非常重要的。