切向和法向加速度(精选)

如何计算物体的切向加速度和法向加速度在物理学中，切向加速度和法向加速度是描述物体运动状态的重要概念。

它们是描述物体在某一瞬时点上加速度的两个分量，切向加速度是物体在曲线轨迹上的加速度分量，而法向加速度则是物体离开直线轨迹时偏离轨迹的加速度分量。

本文将介绍如何计算物体的切向加速度和法向加速度。

一、切向加速度的计算方法切向加速度是物体在曲线轨迹上的加速度分量，可以通过以下公式计算：a_t = (v^2)/r其中，a_t表示切向加速度，v表示物体在曲线上某一瞬时点的速度，r表示曲线的曲率半径。

要计算切向加速度，首先需要确定物体在曲线上的速度，这可以通过速度矢量进行表示。

速度矢量的大小等于物体在曲线上的瞬时速度，而速度矢量的方向等于物体在曲线上的切线方向。

其次，需要确定曲线的曲率半径。

曲率是描述曲线弯曲程度的物理量，其倒数即为曲率半径。

曲率半径越小，曲线的弯曲程度越大。

将物体在曲线上的速度v和曲线的曲率半径r代入上述公式即可计算出切向加速度a_t的数值。

二、法向加速度的计算方法法向加速度是物体离开直线轨迹后产生的向心加速度分量。

在物体沿着曲线运动时，一方面受到切向加速度的作用，另一方面也需要受到法向加速度的作用使得物体保持在轨迹上。

法向加速度的计算方法如下：a_n = (v^2)/r其中，a_n表示法向加速度，v表示物体在曲线上某一瞬时点的速度，r表示物体离开直线轨迹所处位置的曲率半径。

计算法向加速度与计算切向加速度的方法相同，都是通过速度矢量和曲率半径来计算。

三、计算示例现以一个物体沿着半径为2米的圆弧运动作为例子。

首先，需要确定物体在圆弧上某一瞬时点的速度v。

假设物体在该点的速度为3 m/s。

其次，需要求出圆弧曲率半径r，由于是半径为2米的圆弧，所以r=2米。

代入公式：a_t = (3^2)/2 = 4.5 m/s^2a_n = (3^2)/2 = 4.5 m/s^2因此，在半径为2米的圆弧上，该物体的切向加速度和法向加速度均为4.5 m/s^2。

切向加速度和法向加速度
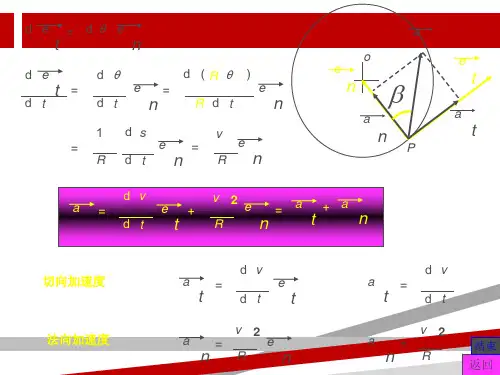
法向加速度：数值上等于速度v的平方除曲率半径r，或角速度ω的平方与半径r的乘积。

法向加速度的计算公式：an=ω^2r=v^2/r。

切向加速度：其值为线速度对时间的变化率。

切向加速度的计算公式：at=dv/dt。

切向加速度公式 at=dv/dt
法向加速度公式 an=v^2/r
切向加速度和法向加速度的区别：
1、切向加速度，改变的是速率的大小。

2、法向加速度，不改变速度的大小，只改变速度的方向。

3、切向加速度是质点作曲线运动时所具有的沿轨道切线方向的加速度。

而法向加速度是质点作曲线运动时，所具有的沿轨道法线方向的加速度。

匀变速圆周运动切向加速度和法向加速度匀变速圆周运动切向加速度和法向加速度是圆周运动中的两种
重要物理量。

切向加速度是指物体在圆周运动中速度方向的变化率，大小等于速度的变化率。

法向加速度是指物体在圆周运动中与圆心连线的方向上的加速度，大小等于速度的平方除以半径，与速度方向垂直。

这两种加速度的方向分别沿切线和法线方向，组成了物体在圆周运动中的总加速度。

在匀变速圆周运动中，切向加速度和法向加速度的大小和方向会随着时间而变化，但它们的大小是常数乘以速度的平方除以半径。

圆周运动中的切向加速度和法向加速度对于理解天体运动、机械运动等领域有着重要的应用。

- 1 -。

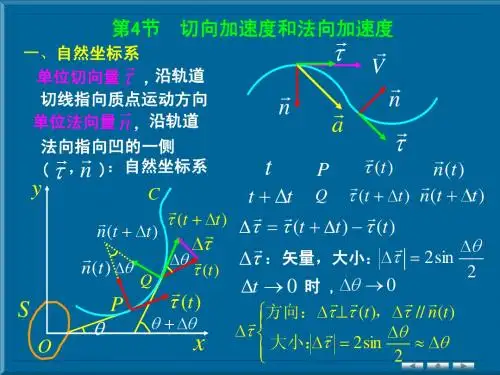
切向加速度和法向加速度－资料类关键信息项：1、切向加速度的定义及相关概念名称：＿___________________________描述：＿___________________________2、法向加速度的定义及相关概念名称：＿___________________________描述：＿___________________________3、切向加速度和法向加速度的计算方法公式：＿___________________________适用条件：＿___________________________4、切向加速度和法向加速度的关系相互影响：＿___________________________关联因素：＿___________________________5、实际应用场景举例场景描述：＿___________________________作用分析：＿___________________________11 切向加速度的定义切向加速度是质点作曲线运动时所具有的沿轨道切线方向的加速度。

它描述了质点速度大小变化的快慢程度。

111 切向加速度的计算公式切向加速度的大小可以通过对速度大小对时间的导数来计算，即：＄a_{t} ＝＼frac{dv}｛dt}＄，其中$v$是速度大小，＄t$是时间。

112 切向加速度的影响因素切向加速度的大小取决于作用在质点上的切向力以及质点的质量。

当切向力增大或质点质量减小时，切向加速度会增大，反之则减小。

12 法向加速度的定义法向加速度是质点作曲线运动时所具有的沿轨道法线方向（指向曲率中心）的加速度。

它反映了质点速度方向变化的快慢。

121 法向加速度的计算公式法向加速度的大小为：＄a_{n} ＝＼frac{v^2}｛r}＄，其中$v$是质点的速度大小，＄r$是曲线运动轨迹的曲率半径。

122 法向加速度的特点法向加速度始终指向曲线的曲率中心，其大小与速度的平方成正比，与曲率半径成反比。