切向和法向加速

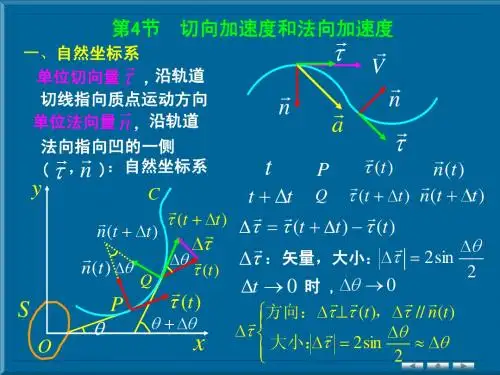
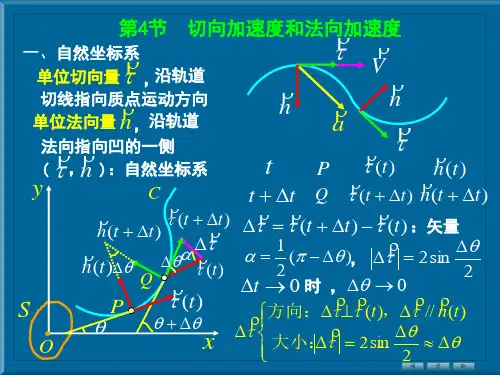
第4节 切向和法向加速度一、自然坐标系单位切向量τ ，沿轨道切线指向质点运动方向单位法向量n ，沿轨道法向指向凹的一侧 （τ ，n ）：自然坐标系 t P )(t τ ， )(t n) t t ∆+ Q )(t t ∆+τ )(t t n ∆+)()(t t t τττ -∆+=∆τ ∆：矢量，大小：2s i n 2θτ∆=∆0→∆t 时 0→∆θ⎪⎩⎪⎨⎧∆≈∆=∆∆⊥∆∆θθτττττ2s i n 2)(//)( 大小：，方向：t n t n ⋅∆≈∆θτ0→∆θ，n n=∆⋅∆=∆∆θθθτlim lim ⇒ n d d =θτdt ds ds d d d dt d d d dt d ⋅⋅=⋅=θθτθθττ ，n d d =θτ，ρθ=d ds ，V dt ds =n V dt d⋅=ρτ 二、切向和法向加速度τ ⋅=V Vn V dt dV dt d V dt dV V dt d dt V d aρττττ2)(+=+===n a a a n t +=τ22dts d dt dV a t ==：切向加速度，速率变化引起的↑V ，0>t a ，沿τ 方向，↓V ，0<t a ，与τ反方向02>=ρV a n ：法向加速度，速度方向变化引起的沿法线指向曲率中心a指向轨迹凹的一侧22222)()(ρV dt dV a a a n t +=+=t n a a tg /=α) 0→∆θ 0→∆θ讨论：（1）直线运动，∞=ρ，0=n a（2）匀速率圆周运动，0==dtdV a t ，R V a n 2=：向心加速度 （3）一般曲线运动及变速率圆周运动，0≠t a ，0≠n a（4）ρ2V a n =⇒na V 2=ρ：计算曲率半径 例：R =800m 的圆形轨道，汽车，静止开始， t a速率均匀增加，t =3（分），V =20m/s 求：t =2（分），a，t a ，n a解：设kt V =，t=3（分）=180s ，V =20m/s k =20/180=1/9， V =t /9)/(111.09/12s m dtdVa t ===t =2（分）=120s ，V =120/9(m/s)RV a n 2==2/222.0s m222/248.0s m a a a n t =+=，t n a a tg /=α=2， 4.63=α第5节 相对运动S '相对于S 作平动运动0r r r+'=' 0r r r ∆+'∆=∆dtr d dt r d dt r d 0+'= V dt r d=：质点在S 系中的速度（绝对速度） V dt r d '='：质点在S '系中的速度（相对速度）00V dtr d =：O '点相对于O 点的速度（牵连速度） V V V+'=：绝对速度=相对速度+牵连速度dt V d dt V d dt V d 0+'= a dt V d=：质点在S 系中的加速度（绝对加速度） a dt V d '='：质点在S '系中的加速度（相对加速度） 00a dtV d=：O '点相对于O 点的加速度（牵连加速度） 0a a a+'=：绝对加速度=相对加速度+牵连加速度如果S '系相对于S 系作匀速直线运动，则00=a ，a a '=例：汽车以雨滴在空气中以10s m / 落，求雨滴相对于汽车的速度解：地面：S ，汽车：S '系 s m /车对地面的速度为牵连速度 大小s m V /200=雨滴对地的速度为绝对速度 0V大小s m V /10=雨滴对车的速度为相对速度 V θ V '根据 0V V V +'= 0V V V-='s m V V V /4.22202=+=' 20==VVtg θ 4.63=θ第6节 圆周运动的角量表示θR s = θ：角坐标，r a d )(t θθ= )(t s s =dt d R R dt d dt ds V θθ===)(dt d θω=：角速度，s rad /R V ω=22dtd R dt d R dt dV a t θω=== 22dtd dt d θωβ==：角加速度，2/s r a d βR a t =，R RR R V a n 2222ωω===讨论： 1、ω不变，匀角速圆周运动（匀速率圆周运动，匀速圆周运动）0==dtd ωβdt d θω=⇒dt d ωθ=⇒⎰⎰=tdt d 00ωθθθ角位移：θ∆=t ωθθ=-0，t ωθθ+=02、β不变：匀变速圆周运动dt d ωβ=⇒d t d βω=，⎰⎰=ωωβω00tdt dt βωω=-0⇒t βωω+=0 t dtd βωθω+==0⇒dt t d )(0βωθ+=⎰⎰+=θθβωθ0)(tdt t d角位移：θ∆=20021t t βωθθ+=-)(2022θθβωω-=- ****************************************************** 匀速圆周运动 匀速直线运动 t ωθθ+=0 Vt x x +=0匀变速圆周运动 匀加速直线运动 t βωω+=0 at V V +=020021t t βωθθ+=- 20021at t V x x +=-)(2022θθβωω-=- )(20202x x a V V -=- ******************************************************。

切向加速度和法向加速度的单位及其转换关系加速度是物体在单位时间内速度变化的量度，通常用字母"a"表示。

在物体运动时，加速度可被分解为切向加速度和法向加速度，用来描述物体在运动过程中分别沿着切线方向和垂直于切线方向的加速度变化情况。

本文将讨论切向加速度和法向加速度的单位及其转换关系。

一、切向加速度的单位及转换关系切向加速度是物体在曲线运动中由于速度方向的变化而产生的加速度，它沿着切线的方向。

切向加速度的单位通常采用米每秒平方（m/s²），表示物体在时间内单位速度增加的量。

在计算切向加速度时，我们可以使用以下公式：切向加速度（a_t）= （v₂ - v₁）/ t其中，v₂和v₁分别表示物体在某一时刻的末速度和初速度，t表示时间。

切向加速度的数值表示速度变化的快慢程度，正值表示速度增加，负值表示速度减小。

在国际单位制中，切向加速度的单位是米每秒平方（m/s²）。

这意味着，如果一个物体的速度在一秒钟内增加了1米每秒，那么该物体的切向加速度就是1米每秒平方。

切向加速度与速度的转换关系如下：切向加速度（a_t）= （dv）/ dt其中，dv表示速度的变化量，dt表示时间的变化量。

二、法向加速度的单位及转换关系法向加速度是物体在曲线运动中由于方向和轨道半径的变化而产生的加速度，它垂直于切线的方向。

法向加速度的单位通常采用米每秒平方（m/s²），表示物体在向心力作用下单位时间内速度变化的量。

在计算法向加速度时，我们可以使用以下公式：法向加速度（a_n）= v² / r其中，v表示物体在某一时刻的速度，r表示物体运动的轨道半径。

法向加速度的数值表示速度变化的快慢程度，正值表示速度增加，负值表示速度减小。

在国际单位制中，法向加速度的单位是米每秒平方（m/s²）。

这意味着，如果一个物体的速度在一秒钟内增加了1米每秒，并且轨道半径为1米，那么该物体的法向加速度就是1米每秒平方。

切向加速度和法向加速度
法向加速度：数值上等于速度v的平方除曲率半径r，或角速度ω的平方与半径r的乘积。

法向加速度的计算公式：an=ω^2r=v^2/r。

切向加速度：其值为线速度对时间的变化率。

切向加速度的计算公式：at=dv/dt。

切向加速度公式 at=dv/dt
法向加速度公式 an=v^2/r
切向加速度和法向加速度的区别：
1、切向加速度，改变的是速率的大小。

2、法向加速度，不改变速度的大小，只改变速度的方向。

3、切向加速度是质点作曲线运动时所具有的沿轨道切线方向的加速度。

而法向加速度是质点作曲线运动时，所具有的沿轨道法线方向的加速度。

切向加速度和法向加速度－资料类关键信息项：1、切向加速度的定义及相关概念名称：＿___________________________描述：＿___________________________2、法向加速度的定义及相关概念名称：＿___________________________描述：＿___________________________3、切向加速度和法向加速度的计算方法公式：＿___________________________适用条件：＿___________________________4、切向加速度和法向加速度的关系相互影响：＿___________________________关联因素：＿___________________________5、实际应用场景举例场景描述：＿___________________________作用分析：＿___________________________11 切向加速度的定义切向加速度是质点作曲线运动时所具有的沿轨道切线方向的加速度。

它描述了质点速度大小变化的快慢程度。

111 切向加速度的计算公式切向加速度的大小可以通过对速度大小对时间的导数来计算，即：＄a_{t} ＝＼frac{dv}｛dt}＄，其中$v$是速度大小，＄t$是时间。

112 切向加速度的影响因素切向加速度的大小取决于作用在质点上的切向力以及质点的质量。

当切向力增大或质点质量减小时，切向加速度会增大，反之则减小。

12 法向加速度的定义法向加速度是质点作曲线运动时所具有的沿轨道法线方向（指向曲率中心）的加速度。

它反映了质点速度方向变化的快慢。

121 法向加速度的计算公式法向加速度的大小为：＄a_{n} ＝＼frac{v^2}｛r}＄，其中$v$是质点的速度大小，＄r$是曲线运动轨迹的曲率半径。

122 法向加速度的特点法向加速度始终指向曲线的曲率中心，其大小与速度的平方成正比，与曲率半径成反比。

第4节切向加速度和法向加速度
切向加速度又称纵向加速度，是指物体行驶过程中的纵向加速度大小。

从线性动力学
角度来看，切向加速度可以定义为物体匀速运动的变速度，即物体线速度加速度的大小。

在实际应用中，切向加速度可以帮助我们了解物体行驶的速度变化，即纵向加速度大小。

当物体维持原有速度而没有变化时，切向加速度的值为零，但是当物体的速度改变时，切向加速度的值就会增加。

例如，运动的小车可以加速或减速，这种速度变化就表现为切
向加速度；电梯精确控制上下行，上行时加速，下行时减速，我们就可以测量出其切向加
速度值。

同切向加速度不同，法向加速度指物体横向运动的加速度大小。

从动力学角度来看，
它是指物体沿着弧形或圆形路径行驶时法向加速度的大小。

在汽车性能测试中，通常可以
测量出汽车的法向加速度值。

一般来说，车辆只有在拐弯时才会产生法向加速度，这时物
体会朝着一个比较小的半径旋转。

从控制的角度来看，切向和法向加速度都是重要的控制参数，可以帮助我们确定物体
的速度和轨迹变化，便于物体运动控制更加准确有效。

可以借助切向加速度来实现物体速
度精确控制，而借助法向加速度，可以使车辆精确跟踪曲线路径。

因此，如果要使机器人
能够实现自主移动，理解切向和法向加速度的物理含义和应用，就非常重要。

切向加速度和法向加速度在车辆行驶中的作用车辆行驶中的切向加速度和法向加速度作用分析车辆行驶中，切向加速度和法向加速度是两个重要的物理概念，它们对车辆的运动轨迹和行驶稳定性起着非常关键的作用。

本文将深入探讨切向加速度和法向加速度在车辆行驶中的作用，并分析其对车辆行驶的影响。

一、切向加速度的作用切向加速度是指车辆在行驶过程中速度方向的变化率，也可以理解为车辆在弯道行驶时的加速度。

切向加速度的作用主要有三个方面。

首先，切向加速度可以控制车辆在弯道行驶中的转向速度。

当车辆进入一个转弯道路时，为了保持行驶轨迹的稳定，司机需要施加足够的切向加速度，使车辆保持在预定的曲线上行驶。

若切向加速度不足，车辆容易偏离预定轨迹，甚至发生侧滑等危险情况。

其次，切向加速度可以增加车辆的抓地力。

在弯道行驶中，车辆受到的向心力会使车辆向外侧倾斜，这时切向加速度可以产生向内的力，抵消向心力的影响，使车辆保持在弯道上行驶。

合理的切向加速度能够有效提高车辆的抓地力，增强行驶稳定性。

再次，切向加速度对车辆的纵向动力学性能有重要影响。

通过控制切向加速度，司机可以灵活应对道路的变化和车辆的需求，实现加速、减速和保持速度的动作。

合理和精确地掌握切向加速度可以提高车辆的驾驶性能，如加速灵敏、平顺换挡等。

二、法向加速度的作用法向加速度是指车辆在行驶过程中速度大小的变化率，它与车辆行驶的方向垂直，也可称为纵向加速度。

法向加速度的作用主要体现在以下几个方面。

首先，法向加速度可以影响车辆的制动性能。

在紧急制动或缓慢停车时，司机需要控制刹车力的大小，使车辆实现平稳的停车动作。

法向加速度的大小和变化率将直接影响到车辆制动的平稳性和安全性。

其次，法向加速度对车辆的悬挂系统和轮胎磨损有一定的影响。

当车辆通过坑洼路面或颠簸路段时，会产生较大的法向加速度，导致车辆悬挂系统承受较大的冲击力，影响乘坐舒适性。

此外，法向加速度还会使轮胎产生较大的摩擦力，引起胎面磨损，影响轮胎寿命。

切向加速度和法向加速度对物体的速度变化有何影响加速度是描述物体速度变化的物理量，包括切向加速度和法向加速度两个方向。

本文将探讨切向加速度和法向加速度对物体速度变化的影响。

一、切向加速度对速度变化的影响切向加速度指的是物体在运动过程中，速度矢量的改变率。

即切向加速度决定了物体在速度方向上的变化。

切向加速度的存在使得物体可以加快或减慢其当前速度。

1. 加速度与速度成正比关系根据牛顿第二定律，物体的加速度与作用力成正比。

当物体受到外力作用时，加速度会产生变化。

如果作用力与速度方向相同，物体将获得正的切向加速度，速度将增加。

如果作用力与速度方向相反，物体将受到负的切向加速度，速度将减小。

2. 加速度与速度平方成正比关系在物体运动过程中，切向加速度也可以通过速度的平方来表达。

根据经典力学理论，物体的运动状态可以用动能和势能来描述。

动能正比于速度的平方，而加速度可以通过能量的变化率来计算。

因此，切向加速度与速度平方成正比，即速度越高，切向加速度对速度变化的影响也就越大。

二、法向加速度对速度变化的影响除了切向加速度，物体运动中还存在法向加速度，即物体在沿着弧度曲线运动时，速度矢量的方向改变。

法向加速度影响着物体速度的方向改变。

1. 法向加速度改变速度方向当物体在弧度曲线上运动时，速度的方向是随着曲线的形状变化的。

此时，物体的速度矢量会受到法向加速度的影响，使速度的方向发生变化。

如果物体受到向心力的作用，法向加速度将指向圆心，使物体的速度方向向圆心靠拢。

相反，如果物体受到离心力的作用，法向加速度将指向远离圆心的方向，使物体的速度方向远离圆心。

2. 法向加速度对速度大小的影响较小与切向加速度不同，法向加速度对于物体速度大小的变化影响相对较小。

因为法向加速度主要影响速度方向，而速度大小则主要由切向加速度决定。

这也解释了为什么在等速圆周运动中，物体的速度大小保持恒定。

综上所述，切向加速度和法向加速度对物体的速度变化具有不同的影响。