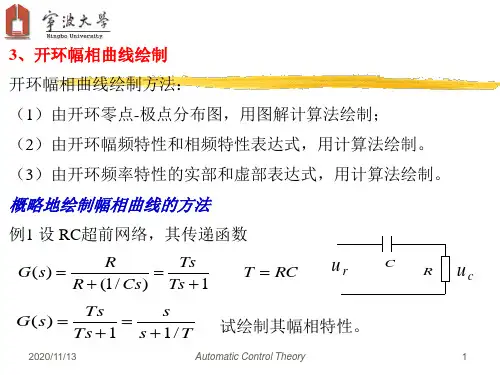
开环幅相曲线绘制
- 格式:ppt
- 大小:491.50 KB
- 文档页数:34



5.3 系统开环频率特性的绘制对自动控制系统进行频域分析时,通常是根据开环系统的频率特性来判断闭环系统的稳定性和估算闭环系统时域响应的各项性能指标,或者根据开环系统的频率特性绘制闭环系统的频率特性,然后再分析及估算时域性能指标。
因此,掌握开环系统的频率特性曲线的绘制和特点是十分重要的。
5.3.1 开环幅相曲线的绘制开环系统的幅相频率特性曲线简称为开环幅相曲线。
准确的开环幅相曲线可以根据系统的开环幅频特性和相频特性的表达式,用解析计算法绘制。
显然,这种方法比较麻烦。
在一般情况下,只需要绘制概略开环幅相曲线,概略开环幅相曲线的绘制方法比较简单,但是概略曲线应保持准确曲线的重要特征,并且在要研究的点附近有足够的准确性。
下面首先介绍幅相频率特性曲线的一般规律与特点,然后举例说明概略绘制开环幅相曲线的方法。
设系统开环传递函数的一般形式为)1()1()()(11++=∏∏-==s T s s K s H s G j vn j v mi i τ )(m n ≥ (5-49)式中,K 为开环增益;v 为系统中积分环节的个数。
则系统的开环频率特性为)1()()1()()(11∏∏-==++=v n j jvmi i Tj j j K j H j G ωωωτωω (5-50)1.开环幅相曲线的起点在低频段当0→ω时,由式(5-50)可得 )90(0lim)(lim)()(lim ︒⋅-→→→==v j vve Kj K j H j G ωωωωωωω (5-51)由式(5-51)可知,当0→ω时,开环幅相曲线的起点取决于开环传递函数中积分环节的个数v 和开环增益K ,参见图5-23(a )。
0型(v =0)系统,开环幅相曲线起始于实轴上的)0,(j K 点。
Ⅰ型(v =1)系统,开环幅相曲线起始于相角为︒-90的无穷远处。
当+→0ω时,曲线渐近于与虚轴的平行的直线,其横坐标[])()(Re lim 0ωωωj H j G V x +→= (5-52)Ⅱ型(v =2)系统,开环幅相曲线起始于相角为︒-180的无穷远处。





第5章线性系统的频域分析法5.1复习笔记本章考点:幅相特性曲线、伯德图的绘制,奈奎斯特稳定判据,稳定裕度计算。
一、频率特性1.定义幅频特性:稳态响应的幅值与输入信号的幅值之比A(ω)。
相频特性:稳态响应与正弦输入信号的相位差φ(ω)。
频率特性:幅频特性和相频特性在复平面上构成的一个完整向量G(jω)=A(ω)e jφ(ω)。
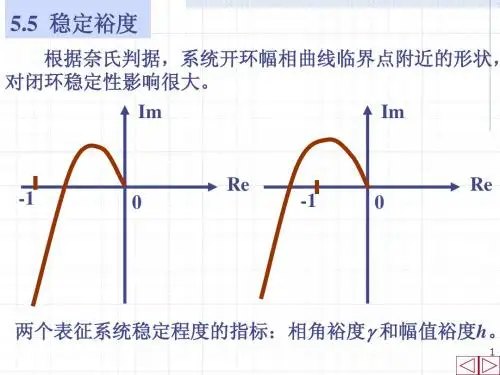
2.频率特性的几何表示法(重点)(1)幅相频率特性曲线(幅相曲线或极坐标图),横坐标为开环频率特性的实部,纵坐标为虚部, 为参变量。
(2)对数频率特性曲线(伯德图),由对数幅频特性曲线、对数幅相频特性曲线两幅图组成:①对数幅频特性曲线的纵坐标表示L(ω)=20lgA(ω),单位是分贝,记作dB;②对数相频特性曲线的纵坐标为φ(ω),单位为度“°”。
(3)对数幅相曲线(尼科尔斯图),横坐标表示频率特性的相角φ(ω),纵坐标表示频率特性的幅值的分贝数L(ω)=20lgA(ω)。
二、典型环节与开环系统的频率特性1.典型环节的频率特性一些主要典型环节的频率特性曲线总结如表5-1-1所示。
表5-1-1典型环节频率特性曲线总结2.开环幅相曲线绘制步骤(1)确定开环幅相曲线的起点(ω=0+)和终点(ω=∞),确定幅值变化与相角变化。
(2)计算开环幅相曲线与实轴的交点。
令Im[G(jωx)H(jωx)]=0或φ(ωx)=∠G(jωx)H(jωx)=kπ(k=0,±1,…)称ωx为穿越频率,而开环频率特性曲线与实轴交点的坐标值为Re[G(jωx)H(jωx)]=G(jωx)H(jωx)。
(3)分析开环幅相曲线的变化范围(象限、单调性)。
3.开环对数频率特性曲线绘制步骤(1)开环传递函数典型环节分解并确定一阶环节、二阶环节的交接频率;(2)绘制低频段渐近特性线:在ω<ωmin频段内,直线斜率为-20vdB/dec;(3)作ω≥ωmin频段渐近特性线,交接频率点处斜率变化表如表5-1-2所示。