3、开环幅相曲线绘制开环幅相曲线绘制方法(1)由开环零点-极点.

自动控制原理总结第一章 绪 论技术术语1. 被控对象:是指要求实现自动控制的机器、设备或生产过程。

2. 被控量：表征被控对象工作状态的物理参量(或状态参量)，如转速、压力、温度、电压、位移等。

3. 控制器：又称调节器、控制装置，由控制元件组成，它接受指令信号，输出控制作用信号于被控对象。

4. 给定值或指令信号r(t)：要求控制系统按一定规律变化的信号，是系统的输入信号。

5. 干扰信号n(t)：又称扰动值，是一种对系统的被控量起破坏作用的信号。

6. 反馈信号b(t)：是指被控量经测量元件检测后回馈送到系统输入端的信号。

7. 偏差信号e(t)：是指给定值和被控量的差值，或指令信号和反馈信号的差值。

闭环控制的主要优点：控制精度高，抗干扰能力强。

缺点：使用的元件多，线路复杂，系统的分析和设计都比较麻烦。

对控制系统的性能要求 :稳定性 快速性 准确性稳定性和快速性反映了系统的过渡过程的性能。

准确性是衡量系统稳态精度的指标，反映了动态过程后期的性能。

第二章 控制系统的数学模型拉氏变换的定义:-0()()e d st F s f t t +∞=⎰几种典型函数的拉氏变换1.单位阶跃函数1(t)2.单位斜坡函数3.等加速函数4.指数函数e -at5.正弦函数sin ωt6.余弦函数cos ωt7.单位脉冲函数(δ函数) 拉氏变换的基本法则 1.线性法则 2.微分法则 3.积分法则1()d ()f t t F s s ⎡⎤=⎣⎦⎰L4.终值定理()lim ()lim ()t s e e t sE s →∞→∞==5.位移定理00()e()sf t F s ττ--=⎡⎤⎣⎦Le ()()atf t F s a ⎡⎤=-⎣⎦L传递函数：线性定常系统在零初始条件下，输出信号的拉氏变换和输入信号的拉氏变换之比称为系统(或元部件)的传递函数。

动态结构图及其等效变换 1.串联变换法则 2.并联变换法则 3.反馈变换法则4.比较点前移“加倒数”；比较点后移“加本身”。

（完整版）⾃动控制原理试题答案∑??=i i i s s Q s H )()(1)(zidpngkongzhi1 闭环系统（或反馈系统）的特征：采⽤负反馈，系统的被控变量对控制作⽤有直接影响，即被控变量对⾃⼰有控制作⽤。

2 典型闭环系统的功能框图。

⾃动控制在没有⼈直接参与的情况下，通过控制器使被控对象或过程按照预定的规律运⾏。

⾃动控制系统由控制器和被控对象组成，能够实现⾃动控制任务的系统。

被控制量在控制系统中．按规定的任务需要加以控制的物理量。

控制量作为被控制量的控制指令⽽加给系统的输⼊星．也称控制输⼊。

扰动量⼲扰或破坏系统按预定规律运⾏的输⼊量，也称扰动输⼊或⼲扰掐⼊。

反馈通过测量变换装置将系统或元件的输出量反送到输⼊端，与输⼊信号相⽐较。

反送到输⼊端的信号称为反馈信号。

负反馈反馈信号与输⼈信号相减，其差为偏差信号。

负反馈控制原理检测偏差⽤以消除偏差。

将系统的输出信号引回插⼊端，与输⼊信号相减，形成偏差信号。

然后根据偏差信号产⽣相应的控制作⽤，⼒图消除或减少偏差的过程。

开环控制系统系统的输⼊和输出之间不存在反馈回路，输出量对系统的控制作⽤没有影响，这样的系统称为开环控制系统。

开环控制⼜分为⽆扰动补偿和有扰动补偿两种。

闭环控制系统凡是系统输出端与输⼊端存在反馈回路，即输出量对控制作⽤有直接影响的系统，叫作闭环控制系统。

⾃动控制原理课程中所讨论的主要是闭环负反馈控制系统。

复合控制系统复合控制系统是⼀种将开环控制和闭环控制结合在⼀起的控制系统。

它在闭环控制的基础上，⽤开环⽅式提供⼀个控制输⼊信号或扰动输⼊信号的顺馈通道，⽤以提⾼系统的精度。

⾃动控制系统组成闭环负反馈控制系统的典型结构如图1．2所⽰。

组成⼀个⾃动控制系统通常包括以下基本元件．给定元件给出与被控制量希望位相对应的控制输⼊信号(给定信号)，这个控制输⼊信号的量纲要与主反馈信号的量纲相同。

给定元件通常不在闭环回路中。

2．测量元件测量元件也叫传感器，⽤于测量被控制量，产⽣与被控制量有⼀定函数关系的信号。

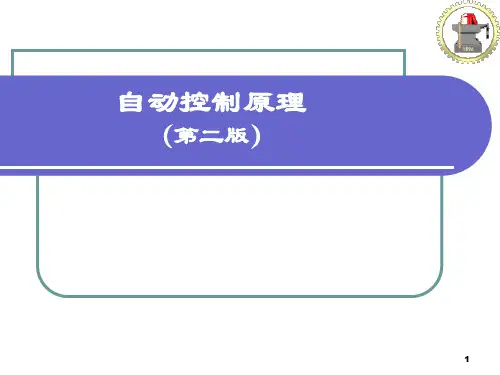
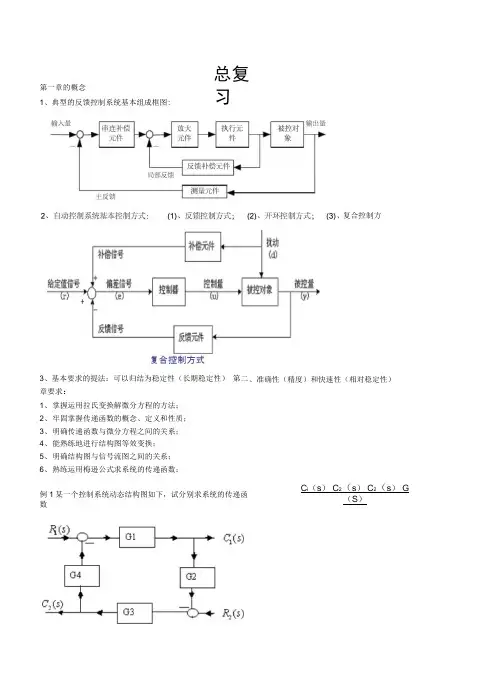
第一章的概念1、典型的反馈控制系统基本组成框图:复合控制方式3、基本要求的提法：可以归结为稳定性（长期稳定性） 第二章要求：1、 掌握运用拉氏变换解微分方程的方法；2、 牢固掌握传递函数的概念、定义和性质；3、 明确传递函数与微分方程之间的关系；4、 能熟练地进行结构图等效变换；5、 明确结构图与信号流图之间的关系；6、 熟练运用梅逊公式求系统的传递函数；例1某一个控制系统动态结构图如下，试分别求系统的传递函数总复习、准确性（精度）和快速性（相对稳定性） C i （s ） C 2（s ） C 2（s ） G（S ）复合控制方C i (s) _ G,s)C 2(s)R i (s)1 - G 1G 2G 3G 4 R i (s)-G 1G 2G 31 - G 1G 2G 3G 4C(s) C(s) E(s) E(S) R(s)，N(s)，R(s)，N(s)例3： 例2某一个控制系统动态结构图如下，试分别求系统的传递函数:EG.7)► * kG 1（S ）G2（S ）C(s) _R(s) 1 G 1(s)G 2(s)H(s) C(s)-G 2 (s) N(s) 一 1 G,S )G 2(S )H(S )r(t) - u 1 (t) i (t) m「1(t ) R 115(t) = J 川dt)-i 2(t)]dtMy)J(t)R 2C(t)二 1 i 2(t)dtC2将上图汇总得到:R(s) +l i (s) +U i (s)l 2(s)U 1(s )*l 2(s)C(s)1 C 1sC(s)I i (s)U i (s)I2G)(b)例5如图RLC 电路，试列写网络传递函数U c (s)/U r (s).例6某一个控制系统的单位阶跃响应为:C(t) =1 -2e't • e ，，试求系统的传递函数、微分方程和脉冲响应。

解：传递函数：2〜、3s +2 八厶八、计 d c(t)丄小dc(t )丄小/八 cdr(t)丄“、 G(s)，微分万程： 2 3 2c(t)=3 2r(t)(s + 2)(s+1)dt 2 dt dt脉冲响应：c(t)二-e‘ 4e'2tk =1例4、一个控制系统动态结构图如下，试求系统的传递函数。

第五章§5-1 引言§5-2频率特性§5-3 开环系统的典型环节分解和开环频率特性曲线的绘制§5-4开环和闭环系统Bode图的绘制方法§5-5 系统稳定性分析§5-6控制系统的相对稳定性分析第五章 控制系统的频率响应分析[教学目的]：掌握利用频域法进行系统分析的一般方法 ，为后面的校正及信号与系统分析打下基础。

掌握系统频率特性分析与系统幅角之间的关系，掌握Nyquist 图和Bode 图的绘制方法，根据系统的Nyquist 图和Bode 图分析系统的性质。

本章的难点是Nyquist 稳定性分析。

[主要容]：一、引言 二、 频率特性 三、 开环系统的典型环节分解和开环频率特性曲线的绘制 四、 频率域稳定判据 五、 稳定裕度 六、 闭环系统的频域性能指标[重点]： 频率特性的基本概念，各种频域特性曲线的绘制，Nyquist 稳定判据的应用，及相对稳定裕度的分析，理解三频段的概念与作用。

[难点]：时域性能指标与频域性能指标之间的相互转换。

闭环频域性能指标的理解与应用[讲授方法及技巧]：联系传递函数，微分方程等数学模型，将频率法和时域分析法、根轨迹法相比较，理解和掌握古典控制系统的完整体系。

准确理解概念，把握各种图形表示法的相互联系。

与时域法进行对比，以加深理解。

§5-1 引言1.时域分析法（特点）1)以传递函数和单位阶跃响应为分析基础构成的一整套解析法为主响应曲线图形分析法为辅的分析方法。

它具有直观、明确的物理意义，但就是运算工作量较大，参数的全局特征不明显。

2) 原始依据－－数学模型，得来不易，也同实际系统得真实情况有差异，存在较多的近似、假设和忽略，有时对于未知对象，还可能要用经验法估计。

3) 对工程中普遍存在的高频噪声干扰的研究无能为力。

4) 在定性分析上存在明显的不足。

5) 属于以“点”为工作方式的分析方法。

2.根轨迹法（特点）1）根轨迹法弥补了时域分析法中参数全局变化时特征不明显的不足，在研究单一指定参数对整个系统的影响时很有用；2）增加零极点（增加补偿器）时，是一种很好的辅助设计工具； 3）以“线”和“面”为工作方式；4）为定性分析提供了一种非常好的想象空间和辅助思维界面。

1自动控制（没有人直接参与），利用（外加的设备或装置），（机器、设备或生产过程的某个工作状态或参数）自动地按照预定的规律运行。

控制系统的基本要求是（稳定性）、（快速性）、（准确性）2在随动系统中，系统分析和设计的重点是研究被控量跟随的（快速性）和（准确性）。

3、人的一切活动现反馈控制的原理，负反馈控制原理（按偏差控制）的原理，闭环负反馈控制原理的精髓是（利用误差消除误差）。

4、经典控制理论常用的分析方法主要有（时域分析法）、（根轨迹分析法）、（频域分析法）三种。

5、自动控制系统基本控制方式有：（开环控制）、（闭环反馈控制）和（复合控制）。

6、按输入量变化规律来看，自动控制系统可分为（恒值控制系统）、（随动系统）和（程序控制系统）。

7、线性定常控制系统的传递函数是零初始条件下，（输出变量）与（输入变量）的拉氏变换之比。

8、组成控制系统结构图的四种基本单元主要包括（信号线）、（引出点）、（比较点）和（方框）。

11、在欠阻尼（10<<ξ）二阶系统中，阻尼比越小，超调量越（大）调节时间越（长） 12、已知某单位反馈系统的开环传递函数为)12)(11.0(50)(++=s s s s G ，则其静态位置误差系数p K =（∞）、静态速度误差系数v K =（50）、静态加速度误差系数a K =（0）。

13、改善二阶系统性能的方法主要有（比例—微分控制）和（测速反馈控制）。

14、组成控制系统结构图的四种基本单元主要包括（信号线）、（引出点）、（比较点）和（方框）。

15、一个线性定常控制系统稳定的充分必要条件是（闭环极点均严格位于s 左半平面）。

16、影响系统稳态误差的因素有：（系统型别）、（开环增益）和（输入信号的形式和幅值）。

17、在斜坡函数的输入作用下，（0）型系统的稳态误差为无穷大；（Ⅱ）型系统的稳态误差为零。

18、根轨迹起于系统开环（极点），终于系统开环（零点）。

19、线性系统的频率特性包括（幅频特性）与（相频特性） 20、已知系统开环传递函数为ss G 10)(=，当频率为2 rad/s 时，则该系统的频率特性为（905-∠）。

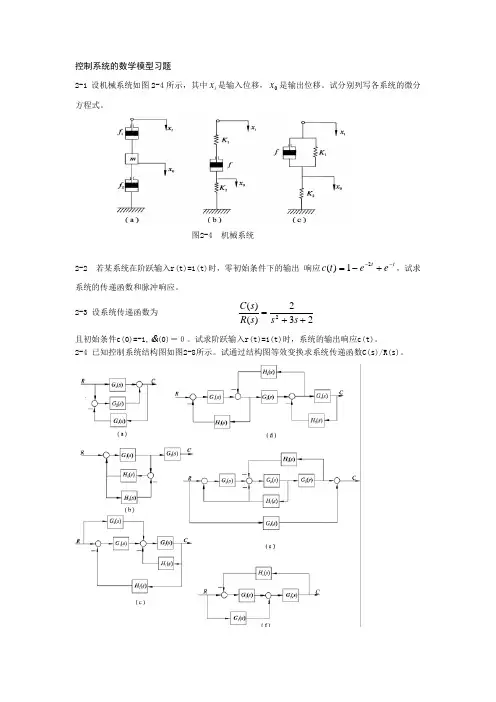
控制系统的数学模型习题2-1 设机械系统如图2-4所示，其中i x 是输入位移，0x 是输出位移。

试分别列写各系统的微分方程式。

图2-4 机械系统2-2 若某系统在阶跃输入r(t)=1(t)时，零初始条件下的输出 响应t t e et c --+-=21)(，试求系统的传递函数和脉冲响应。

2-3 设系统传递函数为 232)()(2++=s s s R s C 且初始条件c(0)=-1,c(0)＝０。

试求阶跃输入r(t)=1(t)时，系统的输出响应c(t)。

2-4 已知控制系统结构图如图2-8所示。

试通过结构图等效变换求系统传递函数C(s)/R(s)。

图2-8 题2-9系统结构图2-5 试简化图2-9中的系统结构图，并求传递函数C(s)/R(s )和C(s)/N(s)。

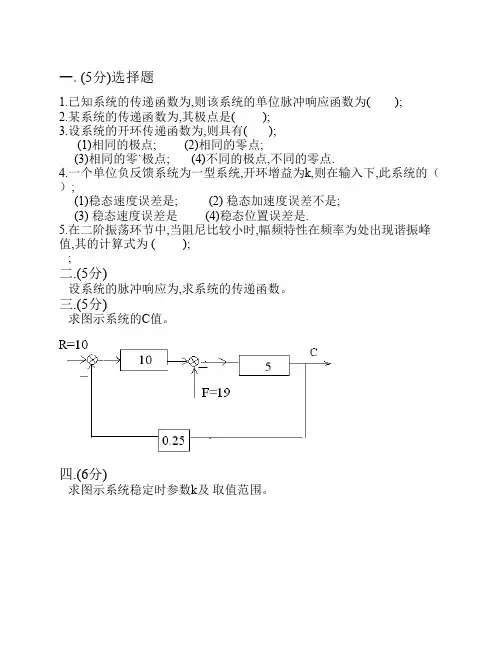
图2-9 题2-10系统结构图线性系统的时域分析法习题3-1 已知系统脉冲响应)1(1.0)(3/t e t c --=,试求系统闭环传递函数Φ(s)3-2 设单位负反馈系统的开环传递函数为)6.0(14.0)(++=s s s s G ,试求系统在单位阶跃输入下的超调量σ%,上升时间t r ,峰值时间t p 和调节时间t s3-3 已知系统特征方程为s 4+2s 3+Ts 2+10s+100=0,试按稳定要求确定T 的取值范围. 3-4 单位负反馈系统的开环传递函数如下:(1) ;)15.0)(11.0(10)(++=s s s G (2) )11.0()15.0(8)(2++=s s s s G , 试求输入为2)(,)(),(1)(t t r t t r t t r ===时系统的稳态误差.3-5 已知控制系统如图所示,试求r(t)=t,n(t)=1(t)时系统的稳态误差.3-6 控制系统如图所示,其中n(t)=1(t). 试问能否选择一个合适的K 1值,使系统在扰动作用下的稳态误差值为?099.0-=ss e线性系统的频域分析法习题P161-1645-1 已知单位反馈控制系统的开环传递函数为,11)(+=s s G 试求出闭环系统在输入信号t t r 2sin )(=作用时的稳态输出;5-2 概略绘制下列传递函数的幅相频率特性曲线:(1)2)(s K s G =; (2))2(4)(+=s s s G ;5-3 绘制下列传递函数的对数幅频特性曲线:(1))11.0)(12.0)(1(2)(+++=s s s s G (2))116.016.0()1(10)(2+++=s s s s s G 5-4 已知最小相位系统的开环近似对数幅频特性曲线如下图所示,试求其对应的传递函数.(5-8)(a) (b) (c)5-5 某系统的开环传递函数)13)(12)(1(10)()(+++=s s s s H s G ,分析: (1) 概略绘制开环系统的幅相频率特性曲线;(2) 用奈氏判据判别闭环系统的稳定性.5-6 某系统其结构图和开环幅相曲线如图(a)、(b)所示，图中2)1(1)(+=s s s G 23)1()(+=s s s H ，试判断系统的稳定性，并求出闭环特征方程正实部根的个数。

开环幅相曲线是指在开环系统中，输出信号的振幅与相位随输入信号频率的变化关系。

它是评估系统稳定性和频率响应的重要工具。

在本文中，我将详细介绍开环幅相曲线的概念、作用和构建方法。

一、开环幅相曲线的概念开环幅相曲线是描述开环系统频率响应的一种图形表示方法。

它展示了系统对不同频率输入信号的增益和相位特性。

通过观察开环幅相曲线，我们可以了解系统在不同频率下的响应情况，进而判断系统的稳定性和频率补偿的需要。

二、开环幅相曲线的作用1. 系统稳定性评估：开环幅相曲线可以帮助我们评估系统的稳定性。

在频率响应中，如果开环增益在某个频率上达到0dB，系统可能存在稳定性问题。

这个频率被称为系统的临界频率，超过这个频率，系统可能会产生振荡。

2. 频率补偿设计：通过观察开环幅相曲线，我们可以确定系统的频率补偿需求。

如果开环增益在特定频率范围内下降较快，我们可以采取相应的频率补偿措施，以提高系统的稳定性和性能。

3. 滤波器设计：开环幅相曲线对于滤波器设计也非常有用。

通过分析开环幅相曲线，我们可以确定滤波器的通带、截止频率和阻带等参数，从而满足特定的滤波要求。

三、开环幅相曲线的构建方法构建开环幅相曲线的一种常用方法是使用频率响应仪器或者模拟仿真软件。

下面是具体的步骤：1. 设计测试信号：选择适当的测试信号，例如正弦波或者脉冲信号。

测试信号的频率应该覆盖感兴趣的频率范围。

2. 测试系统响应：将测试信号输入到待测试系统中，记录输出信号的幅值和相位。

3. 绘制幅相曲线：根据记录的幅值和相位数据，绘制系统的幅相曲线。

通常，幅值使用对数坐标表示，相位使用线性坐标表示。

4. 分析曲线特性：通过观察幅相曲线，分析系统在不同频率下的响应特性。

关注增益的变化和相位的变化，判断系统的稳定性和频率补偿的需求。

四、总结开环幅相曲线是评估开环系统频率响应的重要工具。

它可以帮助我们评估系统的稳定性，并指导频率补偿设计和滤波器设计。

构建开环幅相曲线的方法包括设计测试信号、测试系统响应和绘制幅相曲线。

自动控制原理总复习资料(完美)总复第一章的概念典型的反馈控制系统基本组成框图如下：输出量串连补偿放大执行元被控对元件元件件象－－反馈补偿元件测量元件自动控制系统有三种基本控制方式：反馈控制方式、开环控制方式和复合控制方式。

基本要求可以归结为稳定性（长期稳定性）、准确性（精度）和快速性（相对稳定性）。

第二章要求：1.掌握运用拉普拉斯变换解微分方程的方法。

2.牢固掌握传递函数的概念、定义和性质。

3.明确传递函数与微分方程之间的关系。

4.能熟练地进行结构图等效变换。

5.明确结构图与信号流图之间的关系。

6.熟练运用梅森公式求系统的传递函数。

例1：某一个控制系统动态结构图如下，求系统的传递函数。

C1(s)C2(s)C(s)C1(s)G1(s)G2(s)G3(s)R1(s)R2(s)R1(s)R2(s)传递函数为：C(s) = G1(s)C1(s) / [1 -G1(s)G2(s)G3(s)R1(s)R2(s)]例2：某一个控制系统动态结构图如下，求系统的传递函数。

C(s)C(s)E(s)E(s)R(s)N(s)R(s)N(s)C(s)G1(s)G2(s)-G2(s)传递函数为：C(s) = G1(s)C(s) / [1 + G1(s)G2(s)H(s)N(s)]例3：i1(t)R1 i2(t)R2R(s)+u1(t) c1(t)C1 C2 r(t)I1(s)+U1(s)112+I2(s)将上图汇总得到：R1I1(s)U1(s)C1s r(t)-u(t) = i(t) R U1(s)u(t) = [i(t) - i(t)]dt Cu(t) - c(t) = i(t)Rc(t) = i(t)dtCI2(s)R2KaC(s)1C2s(b)C(s) R(s)+R1C1sR2C2s1Ui(s)1/R11/C1sIC(s)1/R21/C2s10rad/s，试求系统的传递函数、特征方程、极点位置以及阻尼比和固有频率的物理意义。

剪切频率设计开环零极点在控制系统中，频率设计是指根据系统的性能要求和稳定性要求，选择适当的开环控制器参数来实现系统的稳定性和性能指标。

在频率设计中，开环零极点设计是其中一个重要的方面，因为开环零极点的选择直接影响系统的频率响应特性和稳定性。

开环零极点设计是通过调整控制系统的开环传递函数的零点和极点来实现对系统的频率响应特性的控制。

在设计开环系统时，需要考虑系统的零点和极点的位置以及它们之间的关系，以实现所需的频率响应特性。

常见的开环零极点设计方法包括根轨迹设计法、频率域设计法和极点配置设计法等。

在实际应用中，通常会根据系统的具体要求选择合适的设计方法和工具来实现所需的频率响应特性。

根据系统的要求，可以采用不同的开环零极点设计方法来实现对系统的频率响应特性的控制。

在进行开环零极点设计时，通常需要考虑以下几个方面的因素：1.系统的稳定性要求：通过设计系统的开环零极点来实现系统的稳定性要求，包括系统的阻尼比、超调量、上升时间等指标。

2.系统的性能要求：通过设计系统的开环零极点来实现系统的性能要求，包括系统的静态误差、动态响应速度、稳定性裕度等指标。

3.系统的频率响应特性：通过设计系统的开环零极点来实现系统的频率响应特性，包括系统的相位裕度、增益裕度、带宽等指标。

在进行开环零极点设计时，通常需要根据系统的要求选择合适的设计方法和工具来实现系统的频率响应特性和稳定性要求。

常见的开环零极点设计方法包括根轨迹设计法、频率域设计法和极点配置设计法等。

在根轨迹设计法中，通过调整零点和极点的位置，可以实现对系统的频率响应特性和稳定性的控制。

通过绘制根轨迹图，可以直观地看出系统的零点和极点对系统的稳定性和性能的影响，从而选择合适的零点和极点位置来实现系统的要求。

在频率域设计法中，可以通过频率响应函数的分析，得出系统的增益裕度、相位裕度和带宽等指标，来选取合适的零点和极点位置来实现系统的要求。

通过频域分析，可以直接得出系统的频率响应特性和稳定性指标，从而选取合适的开环零极点设计参数。

试卷一一、填空题（每空1分，共15分）自动控制是在___________情况下，利用___________使___________的被控量自动地按预先给定的规律去运动。

对控制系统的基本要求是___________、___________和___________。

线性定常系统的传递函数定义为：初始条件___________时，系统___________拉式变换与系统___________拉式变换之比。

在频率域中表征系统稳定程度的指标是：___________和___________。

若环节的传递函数为s K，则其对数幅频特性L （ω）在零分贝点处的频率数值为______________。

Bode 图中对数相频特性图上的－180o 线对应于奈奎斯特图中的___________。

标志着系统最终可能达到的控制精度，它既与系统的结构及参数有关，也取决于___________的形式及大小。

二、简答题（本题15分，其中第1小题10分，第2小题5分） 试求出下图无源网络的传递函数)(/)(s U s U r c已知系统的闭环特征方程为0)3)(2)(1(=++++k s s s 试确定系统稳定时K 的取值范围 三、计算题（本题40分，其中第1、3小题15分，第2小题10分） 已知系统的结构图如下图所示。

若)(1)(t t r =时，试求 （1）当0=f K 时，求系统超调量%σ及调节时间s t。

（2）当0≠f K 时，若要使超调量%σ＝20％，试求f K 应为多大？并求出此时的调节时间s t 的值。

（3）比较上述两种情况，说明内反馈s K f 的作用是什么？系统结构图如+-ru u 1C 2R-R (s )C (s f K s-1000.5s(s+2)下图所示。

当输入信号)(1)(t t r =，干扰信号)(1)(t t n =时，求系统总的稳态误差系统结构图若下图所示，求传递函数)(/)(s R s C ，)(/)(s R s E四、图解题（本题30分，其中第1小题20分，第2小题10分） 已知某最小相位系统开环对数幅频特性如图所示。

一、填空题1 闭环控制系统又称为反应控制系统。

2 一线性系统，当输入是单位脉冲函数时，其输出象函数与 传递函数 相同。

3一阶系统当输入为单位斜坡函数时，其响应的稳态误差恒为 时间常数T 。

4 控制系统线性化过程中，线性化的精度和系统变量的 偏移程度 有关。

5 对于最小相位系统一般只要知道系统的 开环幅频特性 就可以判断其稳定性。

6 一般讲系统的位置误差指输入是 阶跃信号 所引起的输出位置上的误差。

7 超前校正是由于正相移的作用，使截止频率附近的 相位 明显上升，从而具有较大的稳定裕度。

8 二阶系统当共轭复数极点位于 +-45度 线上时，对应的阻尼比为0.707。

9 PID 调节中的“P 〞指的是 比例 控制器。

10 假设要求系统的快速性好，那么闭环极点应距虚轴越_ 远 越好。

11 在水箱水温控制系统中，受控对象为_水箱 ，被控量为_水温 。

12 自动控制系统有两种根本控制方式，当控制装置与受控对象之间只有顺向作用而无反向联系时，称为_ 开环控制方式 ；当控制装置与受控对象之间不但有顺向作用而且还有反向联系时，称为_ 闭环控制方式 ；含有测速发电机的电动机速度控制系统，属于_ 开环控制方式 。

13 稳定是对控制系统最根本的要求，假设一个控制系统的响应曲线为衰减振荡，那么该系统_ 稳定 _。

判断一个闭环线性控制系统是否稳定，在时域分析中采用_ 劳斯判据 _；在频域分析中采用_ 奈氏判据 _。

14、传递函数是指在_ 零 _初始条件下、线性定常控制系统的_ 输入拉式变换 _与_ 输出拉式变换 _之比。

15 设系统的开环传递函数为2(1)(1)K s s Ts τ++，那么其开环幅频特性为_ _，相频特性为 _-180-arctan 〔tw-Tw 〕/1+tTw _。

16 频域性能指标与时域性能指标有着对应关系，开环频域性能指标中的幅值穿越频率c ω对应时域性能指标_ 调整时间t _，它们反映了系统动态过程的_快速性 _。

试卷一一、填空题（每空1分，共15分）自动操纵是在___________情形下，利用___________使___________的被控量自动地按预先给定的规律去运动。

对操纵系统的大体要求是___________、___________和___________。

线性定常系统的传递函数概念为：初始条件___________时，系统___________拉式变换与系统___________拉式变换之比。

在频率域中表征系统稳固程度的指标是：___________和___________。

假设环节的传递函数为s K，那么其对数幅频特性L （）在零分贝点处的频率数值为______________。

Bode 图中对数相频特性图上的－180o 线对应于奈奎斯特图中的___________。

标志着系统最终可能达到的操纵精度，它既与系统的结构及参数有关，也取决于___________的形式及大小。

二、简答题（此题15分，其中第1小题10分，第2小题5分） 试求出以下图无源网络的传递函数)(/)(s U s U r c已知系统的闭环特点方程为0)3)(2)(1(=++++k s s s 试确信系统稳固时K 的取值范围 三、计算题（此题40分，其中第一、3小题15分，第2小题10分） 已知系统的结构图如以下图所示。

假设)(1)(t t r =时，试求 （1）当0=f K 时，求系统超调量%σ及调剂时刻s t。

（2）当0≠f K 时，假设要使超调量%σ＝20％，试求f K 应为多大？并求出此刻的调剂时刻s t 的值。

（3）比较上述两种情形，说明内反馈s K f 的作用是什么？R (s )C (s )-2K sN(s )1K系统结构图如以下图所示。

当输入信号)(1)(t t r =，干扰信号)(1)(t t n =时，求系统总的稳态误差系统结构图假设以下图所示，求传递函数)(/)(s R s C ，)(/)(s R s E四、图解题（此题30分，其中第1小题20分，第2小题10分） 已知某最小相位系统开环对数幅频特性如下图。