当前位置：文档之家 › 开环系统频率特性曲线的绘制方法

开环系统频率特性曲线的绘制方法

  • 格式：doc
  • 大小：589.00 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

绘制开环幅相频率特性曲线的教学方法研究

绘制开环幅相频率特性曲线的教学方法研究
绘制开环幅相频率特性曲线的教学方法研究郑长勇安徽建筑大学电子与信息工程学院安徽合肥230601摘要线性控制系统的频率分析法是自动控制原理学习中的一个重要部分而奈奎斯特稳定判据是其中的一个重点内容开环幅相频率特性曲线的绘制是奈奎斯特稳定判据的基础
２ ０ １ ３年 １ １ 月 第３ １ 卷 第 ６ 期
的交点 的确 定
特 性 曲线 与实轴 的交 点 ： 由 Ｑ（ 叫 ） 一０求 出对 应
的 ∞的值 ， 再将 叫值代入到 Ｐ（ ） 表达式 中， 得到的 值 即为频率 特性 曲线 与 实轴交 点 的坐 标 ；
同理 ， 特 性 曲线 与 虚 轴 的 交 点 ： 由 Ｐ（ ） ＝ ＝ ＝ ０求 出对 应 的 的值 ， 再将 ∞值代 入到 Ｑ（ ∞ ） 表达式中， 得 到 的值 即为频率 特性 曲线 与 虚轴 交点 的坐 标 。 注： 问断 点 的问题 。随 着 叫的值 从 ０开 始 不 断 增加 ， 系统 的频率 特 性 曲线 在 某一 点 或某 些 点 处 不 连续 ， 特 别要 注 意这些 不 连续 点 ， 参 看本 文 开环 幅相 频率 特 性 曲线绘 制举 例部 分 中 的例 ４ 。
和虚部 的值及正负性 ， 确定起点坐标及所处的象限。 步骤 二 开环 幅 相频 率特性 曲线 终 点 的确定 将∞ 一＋。 。 分别代入到系统频 率特性 表达式 中的 实部和虚部 ， 分别 求 出实部 及虚部 的值 。根 据 实部 和 虚部 的值 及正负性 ， 确定终点坐标及所处的象限 。 步 骤 三 开环 幅 相频 率 特 性 曲线 与 实轴 、 虚 轴
２ 开 环幅 相频 率特 性 曲线 绘制举 例 例 １ 某 ０型 单 位 反 馈 系 统 Ｇ（ Ｓ ）一
［ 收稿 日期］２ ｏ １ ３ 一Ｏ ６ —１ Ｏ ［ 基金项 目］安徽省 教 育厅 自然科 学 重点 科 研项 目 （ Ｋ Ｊ ２ Ｏ １ ３ Ａ Ｏ ７ １ ） ； 安 徽 省质 量工 程 项 目（ ２ ０ １ ０ ０ ７ ５ ７ ） ； 安 徽 建 筑 大学 教 学 研究 项 目

实验三 系统频率特性曲线的绘制及系统分析

实验三 系统频率特性曲线的绘制及系统分析

《自动控制原理》实践报告实验三系统频率特性曲线的绘制及系统分析熟悉利用计算机绘制系统伯德图、乃奎斯特曲线的方法，并利用所绘制图形分析系统性能。

一、实验目的1．熟练掌握使用MATLAB软件绘制Bode图及Nyquist曲线的方法；2．进一步加深对Bode图及Nyquist曲线的了解；3．利用所绘制Bode图及Nyquist曲线分析系统性能。

二、主要实验设备及仪器实验设备：每人一台计算机奔腾系列以上计算机，配置硬盘≥2G，内存≥64M。

实验软件：WINDOWS操作系统（WINDOWS XP 或WINDOWS 2000），并安装MATLAB 语言编程环境。

三、实验内容已知系统开环传递函数分别为如下形式， （1）)2)(5(50)(++=s s s G （2）)15)(5(250)(++=s s s s G（3）210()(21)s G s s s s +=++ （4）)12.0)(12(8)(++=s s s s G （5）23221()0.21s s G s s s s ++=+++ （6）)]105.0)125.0)[(12()15.0(4)(2++++=s s s s s s G 1．绘制其Nyquist 曲线和Bode 图，记录或拷贝所绘制系统的各种图形； 1、 程序代码： num=[50];den=conv([1 5],[1 2]); bode(num,den)num=[50];den=conv([1 5],[1 2]); nyquist(num,den)-80-60-40-20020M a g n i t u d e (d B)10-210-110101102103-180-135-90-450P h a s e (d e g )Bode DiagramFrequency (rad/sec)-1012345-4-3-2-11234Nyquist DiagramReal AxisI m a g i n a r y A x i s2、 程序代码： num=[250];den=conv(conv([1 0],[1 5]),[1 15]); bode(num,den)num=[250];den=conv(conv([1 0],[1 5]),[1 15]);-150-100-5050M a g n i t u d e (d B )10-110101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)nyquist(num,den)3、 程序代码： num=[1 10];den=conv([1 0],[2 1 1]); bode(num,den)-150-100-50050100M a g n i t u d e (d B)10-210-110101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)-1-0.9-0.8-0.7-0.6-0.5-0.4-0.3-0.2-0.10-15-10-551015System: sys Real: -0.132Imag: -0.0124Frequency (rad/sec): -10.3Nyquist DiagramReal AxisI m a g i n a r y A x i snum=[1 10];den=conv([1 0],[2 1 1]); nyquist(num,den)-25-20-15-10-5-200-150-100-5050100150200Nyquist DiagramReal AxisI m a g i n a r y A x i s-100-5050100M a g n i t u d e (d B )10-210-110101102-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)4、 程序代码： num=[8];den=conv(conv([1 0],[2 1]),[0.2 1]); bode(num,den)-18-16-14-12-10-8-6-4-20-250-200-150-100-50050100150200250Nyquist DiagramReal AxisI m a g i n a r y A x i snum=[8];den=conv(conv([1 0],[2 1]),[0.2 1]); nyquist(num,den)5、 程序代码： num=[1 2 1]; den=[1 0.2 1 1]; bode(num,den)num=[1 2 1];den=[1 0.2 1 1]; nyquist(num,den)-40-30-20-10010M a g n i t u d e (d B )10-210-110101102-360-270-180-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)-2.5-2-1.5-1-0.500.51 1.5-3-2-1123Nyquist DiagramReal AxisI m a g i n a r y A x i s-100-5050100M a g n i t u d e (d B )10-210-110101102-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)6、 num=[2 4];den=conv(conv([1 0],[2 1]),[0.015625 0.05 1]); bode(num,den)num=[2 4];den=conv(conv([1 0],[2 1]),[0.015625 0.05 1]); nyquist(num,den)2．利用所绘制出的Nyquist 曲线及Bode 图对系统的性能进行分析：（1）利用以上任意一种方法绘制的图形判断系统的稳定性； 由Nyquist 曲线判断系统的稳定性，Z=P-2N 。

系统开环频率特性的绘制

系统开环频率特性的绘制

5.3 系统开环频率特性的绘制对自动控制系统进行频域分析时，通常是根据开环系统的频率特性来判断闭环系统的稳定性和估算闭环系统时域响应的各项性能指标，或者根据开环系统的频率特性绘制闭环系统的频率特性，然后再分析及估算时域性能指标。

因此，掌握开环系统的频率特性曲线的绘制和特点是十分重要的。

5.3.1 开环幅相曲线的绘制开环系统的幅相频率特性曲线简称为开环幅相曲线。

准确的开环幅相曲线可以根据系统的开环幅频特性和相频特性的表达式，用解析计算法绘制。

显然，这种方法比较麻烦。

在一般情况下，只需要绘制概略开环幅相曲线，概略开环幅相曲线的绘制方法比较简单，但是概略曲线应保持准确曲线的重要特征，并且在要研究的点附近有足够的准确性。

下面首先介绍幅相频率特性曲线的一般规律与特点，然后举例说明概略绘制开环幅相曲线的方法。

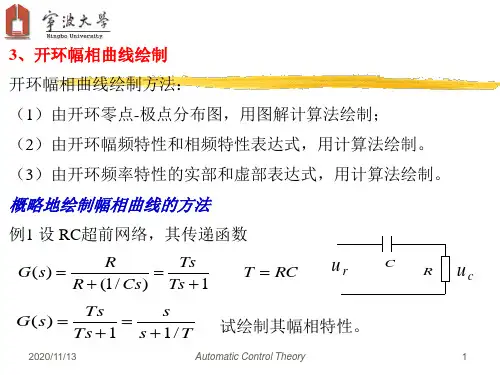
设系统开环传递函数的一般形式为)1()1()()(11++=∏∏-==s T s s K s H s G j vn j v mi i τ )(m n ≥ （5-49）式中，K 为开环增益；v 为系统中积分环节的个数。

则系统的开环频率特性为)1()()1()()(11∏∏-==++=v n j jvmi i Tj j j K j H j G ωωωτωω （5-50）1．开环幅相曲线的起点在低频段当0→ω时，由式（5-50）可得 )90(0lim)(lim)()(lim ︒⋅-→→→==v j vve Kj K j H j G ωωωωωωω （5-51）由式（5-51）可知，当0→ω时，开环幅相曲线的起点取决于开环传递函数中积分环节的个数v 和开环增益K ，参见图5-23（a ）。

0型（v =0）系统，开环幅相曲线起始于实轴上的)0,(j K 点。

Ⅰ型（v =1）系统，开环幅相曲线起始于相角为︒-90的无穷远处。

当+→0ω时，曲线渐近于与虚轴的平行的直线，其横坐标[])()(Re lim 0ωωωj H j G V x +→= (5-52)Ⅱ型（v =2）系统，开环幅相曲线起始于相角为︒-180的无穷远处。

自动控制理论_19开环对数频率特性曲线的绘制

自动控制理论_19开环对数频率特性曲线的绘制

穿越法判断包围圈数 设 N 为开环幅相频率特性曲线穿越（－ 1 ， j0 ） 点左侧负实轴的次数， N ＋表示正穿越的次数（从 上往下穿越）， N －表示负穿越的次数（从下往上 穿越），则
R 2N 2( N N )
5.2 例 系统开环传递函数为 G ( s) H ( s) 2 ( s 2)(s 2s 5)
圈时，F(s)总的相角增量为
n i 1
F ( s) ( s zi ) ( s pi )
i 1
n
( s z1 ) ( s z2 ) ( s zn ) ( s p1 ) ( s p2 ) ( s pn )
s
s zi
B
A
F ( s)
F
F
z 1 p1 z 2
z i 1
j
s
s zi
zi
s
j
B
A
F ( s)
F
F
z 1 p1 z 2
z i 1
S 平面上的闭合曲线 Γs 内部仅有 1 个 F(s) 的零点， F (s) 的其 它零极点如图所示。当闭合曲线Γs上任一点S沿顺时针方向转动一
第五章
频率域方法
5.3
开环对数频率特性曲线的绘制
根据叠加原理，绘出各环节的对数幅频特性 分量，再将各分量的纵坐标相加，就得到整个系 统的开环对数幅频特性；将各环节的相频特性分 量相加，就成为系统的开环对数相频特性。
例
10(0.5s 1) G( s) s ( s 1)(0.05s 1)
1 180 ，即A() 1 （－1，j0）点表示成幅角形式是 ( ) 180 而A(ω)＝1对应于对数幅频坐标图上L(ω)＝0 的水平线； () 180则对应于对数相频坐标图上－ 180°的水平线。因此可以进行坐标系转换。

4第三节系统对数频率特性的绘制

4第三节系统对数频率特性的绘制
m1 −1 m2 −1
2ζ lTlω −ν − ∑ tg T pω − ∑ tg 2 2 p =1 1 − Tl ω 2 l =1 π π ϕ (0) = −ν , ϕ (∞) = −(n − m) 。n = ν + n1 + 2n2 , m = m1 + 2m2 且有： 2 2 由以上的分析可得到开环系统对数频率特性曲线的绘制方 法：先画出每一个典型环节的波德图，然后相加。
G1 ( s ) =
1+ s 1 + 10 s
G1 ( s ) =
1− s 1 + 10 s
最小相位系统
非最小相位系统
对于最小相位系统，幅值特性和相位特性之间具有唯一对应 关系。这意味着，如果系统的幅值曲线在从零到无穷大的全部 频率范围上给定，则相角曲线被唯一确定，反之亦然；但是这 个结论对于非最小相位系统不成立。 非最小相位系统情况可能发生在两种不同的条件下。一是 当系统中包含一个或多个非最小相位环节；另一种情况可能发 生在系统存在不稳定的内部小回路。 一般来说，右半平面有零点时，其相位滞后更大，闭环系 统更难稳定。因此，在实际系统中，应尽量避免出现非最小相 位环节。
[解]：1、k = 10 −3 ,20 log k = −60;ν = 2; ω1 =
1 1 ω3 = = 8, ω 4 = = 20, 0.125 0.05
2、低频渐进线斜率为 − 20ν = −40dB ，过（1，-60）点。 3、高频渐进线斜率为 ：− 20 × (n − m) = −60 4、画出波德图如下
ϕ (ω )
− 45o
− 90o − 135o
1 T1
1 T2
− 20 − 40 − 60 − 80
−40

应用MATLAB绘制系统频率特性曲线

应用MATLAB绘制系统频率特性曲线

G(s)
稳定性。
s3
5系s22.7统4s的 2奈奎斯特曲线，并利用曲线来判别闭环系统的
解 MATLAB仿真程序代码如下：
num1=[ 2.7]；
den1=[1 5 4 2]；
sys1=tf(num1,den1)；
nyquist(sys1)
title('Nyquist图');
运行后，获得如图1-46所示曲线。
自动控制原理
应用MATLAB绘制系统频率特性曲线
1.1用MATLAB绘制系统开环对数频率特性 对于连续系统，用MATLAB函数绘制系统开环对 数频率特性的函数命令调用格式有 Bode（sys） Bode（sys，w） Bode（sys1，sys2,…，sysN） Bode（sys1，sys2,…，sysN，w） [mag，phase，w]=Bode(sys)
例1-15 绘制一阶惯性环节
的G(s奈) 奎3斯特图。
5s 1
解 MATLAB仿真程序代码如下：
G=tf(3，[5 1])；
nyquist(G)；Fra bibliotekhold on；
title('Nyquist图')；
运行后，获得如图1-45所示曲线。
图1-45 例1-15系统极坐标曲线图
例1-16 用函数nyquist(sys)绘制开环传递函数为
bode(num,den);hold on；
end
grid
获得振荡环节伯德图如图1-43所示，
图1-43 例1-13开环系统伯德图
如果希望求取控制系统的增益裕量 、相位GM裕量 界频率（也称PM交叉频
率） 、穿越g频率 ，可以使c 用margin函数 计算控制系统的相关稳定裕度值。

3、开环幅相曲线绘制开环幅相曲线绘制方法(1)由开环零点-极点

3、开环幅相曲线绘制开环幅相曲线绘制方法(1)由开环零点-极点

)
2型系统包含两个积分环节，例如
G(s)
K
s 2 (T1s 1)(T2 s 1)
G( j)
K
K
( j) 2 ( jT1 1)( jT2 1) 2 1 T12 2
() 180 arctgT1 arctgT2
2020/11/13
Automatic Control Theory
e j ( )
1 T22 2
起点： G( j0) A(0) K 终点： G( j) A() 0
G( j0) (0) 0o G( j) () 180o
与实轴的交点： Q(x ) 0 Q() K (T1 T2 ) /(1 T12 2 )(1 T22 2 ) 0
x 0
与虚轴的交点： P( y ) 0
P() K (1 T1T2 2 ) /(1 T12 2 )(1 T2 2 2 )
Hale Waihona Puke 变化的。例如P(0) K
0
G(s)
K(T1s 1)
(T2 s 1)(T3s 1)(T4 s 1)
n 3, m 1
G( j0) K0o , G( j) 0(1 3)90o 0 180o
2020/11/13
Automatic Control Theory
7
开环传递函数含有积分环节时的开环幅相曲线
T RC u r
C R uc
G(s) Ts s Ts 1 s 1/ T
试绘制其幅相特性。
2020/11/13
Automatic Control Theory
1
G( j) j T
T
j
(
arc
tgT
)
e2
jT 1 1 2T 2

开环系统频率特性曲线的绘制方法

开环系统频率特性曲线的绘制方法

开环系统频率特性曲线的绘制方法（一) 已知系统开环传递函数G k （s )，绘制Nyquist 曲线(开环幅相曲线) 一、ω：0＋→＋∞1、由已知的G k (s ）求()()k k s j G j G s ωω==，A (ω），φ(ω） ，P (ω），Q (ω）;112112221122121122121121122211221211221222222222(1)[(1)2](1)[(1)2]()()(1)[(1)2](1)[(1)2]m m m m j k j kk k j k j kk k k vn n n n i l i l lli l i l l lj T j j T j k G j j j T j j T j ωωωωωξωξωωωωωωωωωωωξωξωωωω+-+---=+-+---∏∏∏∏∏∏∏∏ （1）式中:分子多项式中最小相位环节的阶次和为111212m m m =+，分子多项式中非最小相位环节的阶次和为212222m m m =+， 分母多项式中最小相位环节的阶次和为111212n n n v =++， 分母多项式中非最小相位环节的阶次和为212222n n n =+,分子多项式阶次之和为12m m m =+，分母多项式阶次之和为12n n n =+。

注:式中仅包含教材p192所列5种非最小相位环节,不包含形如1Ts -、11Ts -、22121nns s ξωω+-、2221nns s ξωω+-等非最小相位环节。

2、求N 氏曲线的起点当ω→0＋时，（1）式可近似为：0lim ()()k vk G j j ωωω+→→（2）于是，N 氏曲线的起点取决于开环放大系数k 和系统的型v 。

① 当0v =时，N 氏曲线起始于实轴上的一点(k ，0)或（－k ，0）； ② 当0v >时，N 氏曲线起始于无穷远点：0k >时，沿着角度()2v πϕω=-⨯起始于无穷远点;0k <时,沿着角度()2v πϕωπ=--⨯起始于无穷远点。

开环伯德图的绘制

开环伯德图的绘制
20dB / dec 40 20 40dB / dec 20dB / dec 40dB / dec
( ) 90 arctan

2
arctan arctan

10
arctan

20
L() 0 A(c ) 1
c ?
?
g ?
h?
G( j )
1
2
10
100

1 1 G( j ) 100 (0.5 j 1) j ( j 1)
一个比例环节、积分环节、一阶惯性环节 和一阶微分环节构成
转角频率分别为 1
1 2 2 T2
1 1 T1
3
开环伯德图的绘制
L( ) 20dB / dec
40 20 40dB / dec 20dB / dec
G( s)
50( s 2) s( s 1)
50( j 2) G( j ) j ( j 1)
( ) ( j 2) j ( j 1) arctg 90 arctg
2
1
2 2
10 10
100 100
0.1
Байду номын сангаас1 2
( )
-90
10
100
1
( )
-92.8 -108.4 -108.4 -95.6 -90.5

4
-120
开环伯德图（习题一）
系统对数幅频特性如图所示，确定传递函数
L( ) 20dB / dec
0
20 20dB / dec
1. 确定每一个环节的转角频率30 2. 找到对应的典型环节 3. 确定变量的值

5.3 开环频率特性曲线的绘制

5.3 开环频率特性曲线的绘制
20 40log
B、低频渐近线的参考点
10(1 j ) 2 G ( s) 2 1 2 ( j 1)1 j 2 4 20 20

为计算方便，取 =1。此时，其相应的复制对数幅值为
0
180
1 j
90
90
90
270
( )
（4）与实轴的交点
令
Im[G( j )] 0
得
1 2 0
此时，与负实轴相交于
1
1 x 0.833 1.2
（5）幅相频率曲线（: 0 ） 的大致走向：
A、在第3、2象限。 B、 = 0 时，以x = -1.2为渐 近线，且
90 90 0 180
1 1 jT2
K
0 0 0
( )
（4）与实轴的交点
令
ImG( j ) 0
有
(T1 T2 ) 0

0
这意味着，除 0 外，曲线与实轴不相交。
（5）幅相频率曲线（: 0 ）的 大致走向： A 在第4、3象限。 B 除 = 0 外，幅相曲线与实轴 不相交。 C 由于该系统由2个惯性环节构 成，所以幅相曲线的幅值随频率的 增加是“单调”减小的。
5[(6 2 ) j5] 2 2 , 5 ( 6 ) 0 , 令 Im[ G ( j )] 0 , 即 1, 1 G( j) 2 (1 j) 5(5 j5) G( j1) 25与负实轴相交于 25处。 (1 j)
【例5-3】绘制如下非最小相位开环传递函数的幅相频率 特性曲线。
2s 1 G( s) s( s 1)

5-2(2) 开环系统的频率特性

5-2(2) 开环系统的频率特性

分子分母同乘以 1
•
K [(an 1bm1 2 1) (bm1 an 1 )( j )] 2 [a n2 1 2 1] 2型系统， 2
K (an 1bm1 2 1) U ( ) 2 (an2 1 2 1)
1
2
1
3
2
所以，开环频率特性为：
G ( j ) A( ) e j ( ) G1 ( j ) G2 ( j ) G3 ( j )
A1 ( ) A2 ( ) A3 ( ) e j ( ) ( ) ( )
1 2 3
开环幅频特性 开环相频特性
第五章 线性系统的频域分析法
第二节 典型环节与开环系统的 频率特性
5-2-2 开环系统频率特性的绘制
项目 内 容
教 学 目 的 数坐标图的绘制方法。
掌握控制系统的概略极坐标图和渐近线形式的对
教 学 重 点 标图的绘制。
控制系统的概略极坐标图和渐近线形式的对数坐
教 学 难 点 渐近线形式的对数坐标图幅频特性的绘制。
i 1
n
对数幅频特性和相频特性都符合叠加原则。
K 例题2：设系统的开环传递函数 G( s) H ( s) sT1 s 1T2 s 1
（T1 ＞T2 ＞ 0，K ＞ 0），试绘制系统开环对数频率特性曲线。 解： 因为系统的开环频率特性为：G( j ) 1）对数幅频特性
K j ( jT1 1)( jT2 1)
0
lim G ( j ) K0

lim G ( j ) 0 180
曲线与坐标轴的交点
可由G（jω）=0分别求得曲线与实轴或虚轴的交点:（也可能不存在 交点，而有渐近线的情形，如本例和P201例5的情况）

开环幅相频率特性曲线和对数相频特性曲线的完整画法

开环幅相频率特性曲线和对数相频特性曲线的完整画法

开环幅相频率特性曲线和对数相频特性曲线的完整画法一般情况下，以X轴为频率，Y轴为幅度和相位，将开环幅相特性曲
线画成两条曲线，分别为幅度特性曲线和相位特性曲线。

1.幅度特性曲线：以频率（角频率）为X轴，以幅度为Y轴，表示系
统输出信号与输入信号之间的幅度比值或增益。

曲线上沿频率增加时，增
益也会增大，但是增大的幅度会减小，因此，在此曲线上，增益逐渐降低，形成一个弓形曲线。

2.相位特性曲线：以频率（角频率）为X轴，以相位为Y轴，表示系
统输出信号与输入信号之间的相位差。

曲线上沿频率增加时，相位差也会
逐渐增大，相位曲线与幅度曲线的关系是一种折线图，但相位差的增加是
随着频率的函数变化。

对数相频特性曲线:
以对数频率（角对数频率）为X轴，以幅度为Y轴，表示系统输出信
号与输入信号之间的幅度比值或增益。

曲线上沿频率增加时，增益也会增大，但是增大的幅度会减小，因此，在此曲线上，增益也会逐渐减小，形
成一个弓形曲线。

自动控制_05c开环频率特性曲线的绘制

自动控制_05c开环频率特性曲线的绘制

K (1 T1T2 2 ) Q( ) (1 T12 2 )(1 T22 2 )
而 A( ) K
1
1 T
2 1
2

1 1 T
2 2 2
( ) 90 arctanT1 arctanT2 ,
当ω＝0时 P(0) K (T1 T2 ),Q() , A(0) , (0) 90 表 明低频率段的渐近线是一条过实轴－K(T1+T2)点且平行于 虚轴的直线。 当ω→∞时 P() 0, Q() 0, A() 0, () 90 90 90 270 可见，此时高频段是以－270°作为极限角而卷入坐标原点 的。
设系统开环传递函数 G ( s ) 中含有V个积分环节，其相应 的频率特性为 m1 m2 2 2 ( 1 j ) [ ( j ) 2 k k ( j ) 1] i k K i 1 k 1 G ( j ) n1 n2 v ( j ) (1 jT j ) [Tl 2 ( j ) 2 2 lTl ( j ) 1]
图5-26 例5-2系统的幅相频率特性
在绘制系统的开环极坐标时，应注意曲线所具 有的一些特征。例如：当ω→0时低频段曲线从何 处出发？而当 ω→∞时的高频段特性曲线以什么姿 态卷向原点？曲线在ω值为多大时跨越实轴或虚轴？ 跨越点的坐标值如何？等等。后两个问题我们已经 作过说明，下面讨论前两个问题。
K (1 jT1 )(1 jT2 ) G ( j ) (1 jT1 )(1 jT2 )(1 jT1 )(1 jT2 )
K [(1 T1T2 2 ) j (T1 T2 ) ] 2 2 2 2 (1 T1 )(1 T2 ) K (1 T1T2 2 ) K (T1 T2 ) j 2 2 2 2 (1 T1 )(1 T2 ) (1 T12 2 )(1 T22 2 )

5.3开环系统频率特性的绘制详解

5.3开环系统频率特性的绘制详解
2 2 i 1 k 1 m1 m2
20 lg 20 lg 1 Tp 2 20 lg (1 Tl 2 ) 2 (2 lTl ) 2
2 2 p 1 l 1
n1
n2
2 k k 相频特性： ( ) tg i tg 2 2 1 k i 1 k 1

0.2 3.85 -5.77
1 5
0
5 6
0.8 -0.79 -1.72

0 0
( ) tg 1 tg 15 相角：
0 ( ) 0

0.2 -56.31

1 5
0.8
-114.62

-180
-90
用上述信息可以大致勾勒出奈氏图。
Thursday, October 11, 2018
1 1 1 4, 2 2,20lg k 20dB 则， T1 T2
2、低频渐进线：斜率为 20 0dB，过点（1，20）
3、波德图如下：
A( )
20
40
4 60
1
2
10
lg
Thursday, October 11, 2018
16
40 60
2
4
3
k (1 jT1 )(1 jT2 ) 试列出实频和虚频特性的表达式。当 k 1, T1 1, T2 5 绘制奈氏 G( j ) [例5-1]设开环系统的频率特性为：
图。
k (1 jT1 )(1 jT2 ) k (1 T1T2 2 ) 解：G( j ) 2 2 2 2 2 2 (1 T1 )(1 T2 ) (1 T1 2 )(1 T2 2 ) k (T1 T2 ) j P( ) jQ( ) 2 2 2 2 (1 T1 )(1 T2 )

BODE图的讲解

BODE图的讲解

注意：K不影响 表达式。
§5.3.2
开环系统对数频率特性 ( Bode)
非最小相位系统
—— 在右半s平面存在开环零点或开环极点的系统 ★ 非最小相角系统未必不稳定 ★ 最小相角系统由L()可以惟一确定G(s) 非最小相角系统由L()不能惟一确定G(s)
课程小结
绘制开环系统Bode图的步骤
1 G ( j ) ( ) j
( ) 90
L( ) 20 lg
当
( )
( ) 90 *
⑷ 惯性环节
1 G ( j ) 1 jT
L( ) 20lg 1 2T2
( ) arctan T
§5.3.1
⑸ 一阶微分
Bode图介绍
§5.3
Bode图介绍
对数频率特性 ( Bode)（2）
横轴
按 lg 刻度，dec “十倍频程” 按 标定，等距等比
坐标特点
纵轴
L( ) 20lgG( j )
dB “分贝”
⑴ 幅值相乘 = 对数相加，便于叠加作图； (2) 可在大范围内表示频率特性；
特点 (3) 使各个频段（分别关系到系统各种性能）都
基准点 ( 1, 斜率
L(1) 20l g K )
20 v dB de c
复合微分 +20dB/dec ⑷ 叠加作图 振荡环节 -40dB/dec 二阶 复合微分 +40dB/dec
0.2 惯性环节 -20 0.5 一阶复合微分 +20 1 振荡环节 -40
§5.3.2
当 1
自动控制原理
§5. 线性系统的频域分析
§5.1 §5.2
§5.3
频率特性的基本概念 幅相频率特性（Nyquist图）

第四章 频域分析(第三节)1

第四章 频域分析(第三节)1
v
G (s) =
jt m w )
? ( j w ) (1 + jT1 w )(1 + jT 2 w ) 鬃 (1 + jT n - v w )
(n
m)
其分母阶次为n-m，分子阶次为m，v=0，1，2…， 乃奎斯特图具有以下特点： (1) 当ω=0时，乃奎斯特图的起点取决于系统的型次：
0型系统(v=0) 起始于正实轴上某一有限点；
由系统的频率特性
G ( jw ) = = K j w (1 + jT w ) - KT 1+ T w
2 2
= - K
K j w (1 - jT w )
( j w ) (1 + jT w )(1 - jT w )
w (1 + T w
2 2
2
+ j
)
- KT
则系统的实频特性为
U (w ) = R e 轾 ( jw ) = G 2 2 臌 1+ T w
ω=0

Im
K (T1T2 ) T1 T2
3 2
[G ( j )]
O ω=∞
Re
例 4-6 已 知 系 统 的 开 环 传 递 函 数 G (s) =
K (1 + T1 s ) s (1 + T 2 s )
(T1＞ T 2 ) , 试 绘 制 其 N y q u i s t 图 。
解 系统是由一个比例环节﹑一个积分环节﹑ 一个一阶微分环节和一个惯性环节串联组成， 其频率特性为 K (1 + jT1 w ) G ( jw ) = ( j w )(1 + jT 2 w ) = K (T1 - T 2 )
(1 + T 2 w

5-2频率特性曲线的绘制

5-2频率特性曲线的绘制

由图可见无论是欠 阻尼还是过阻尼系 统，其图形的基本 形状是相同的。 当过阻尼时，阻尼 系数越大其图形越 接近圆。
-2
0.2
04:54 16
（2）Bode图（对数频率特性）：
幅频特性为：
A( )
1 (1 T 2 2 )2 (2T )2
相频特性为：
( ) tg 1
04:54
1 称为转折频率。斜率为-40dB/Dec。 T
17
1 相频特性： ( ) tg
2 T 1 T 2 2
1 , ( ) ; , ( ) 。 T 2
几个特征点： 0, ( ) 0;
下图是当T=1时的图
G ( j ) jT 1
j 0
（1）Nyquist图（幅相频率特性）：
ω
1
A( ) 1 T 2 2 , ( ) tg 1T
（2）Bode图（对数频率特性）：
L( ) 20lg 1 T 2 2
对数幅频特性（用渐近线近似）：
L( ) 0 20lg A( ) 0 L( ) 20lg A( ) 20lgT
20
16 12

0.1 0.2 0.3 0.5 0.7 1 .0
10
8 4 0 -4 -8
1 10T 1 5T 1 2T 1 T 2 T
0
渐近线

0.1 0.2 0.3 0.4 0.5 0.6
-10
0 .7 0 .8 1 .0
04:54
低频段渐进线 高频段渐进线
12
这是斜率为+20dB/Dec的直线。

4.4.2 开环频率和奈奎斯特图

4.4.2 开环频率和奈奎斯特图

3. 如果Nyquist图经过(-1,j0)，则系统临界稳定。
4. 如果Nyquist图的的变化范围为0到＋∞， 那么Z＝P－2N
推论：若Nyquist图顺时针包围(-1,j0)点，则系统一定不稳定。
(N = P － Z , 若N<0，P不会为负值，则必有Z ≥1)
k 例4-6 已知开环传递函数 G0 ( j ) ( T1 j 1 )( T2 j 1 ) 判断系统稳定性
C'
s 的第（4）部分无穷小半圆弧在 GH平面上的映射为顺时针旋转 的无穷大圆弧，旋转的弧度为 弧度。图 4-9（a）、（b）分别表 示当 v=1和v=2时系统的奈氏曲线，其中虚线部分是s 的无穷小半圆 弧在GH平面上的映射。

( 2)
j
S
R
0 I m
GH
k , k 100 例4-7 G0 ( j ) ( j 1)(0.5 j 1)(0.2 j 1)
画Nyquist图：
1
0
G0 ( j 0 ) 10000 G ( j ) 0 2700
2

0 单调变化
与实轴有交点，为－7.9
(分母有理化，按虚实部讨论)
j S 平面 j
2 1 - j D形围线 3
s
半径无限大
j j
S平面
Im G 平面 0

j
-1
Re
N= -2
Im G 平面 0
N= 0 • 注意域的映射关系
-1
Re
Nyquist稳定判据(在G0 (s)平面上) : 必须使得Z=0(Z为不稳定闭环特征根的个数)。 1. 若系统开环稳定，则闭环系统稳定的条件是Nyquist图不包 围(-1,j0)点。 （N = P － Z = 0－0 ＝ 0) 2. 闭环系统稳定的充要条件是 N = P ( N = P － Z = P 所以 Z = 0 )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

开环系统频率特性曲线的绘制方法(一) 已知系统开环传递函数G k (s )，绘制Nyquist 曲线（开环幅相曲线） 一、ω：0＋→＋∞1、由已知的G k (s )求()()k k s j G j G s ωω==，A (ω)，φ(ω) ，P (ω)，Q (ω)；112112221122121122121121122211221211221222222222(1)[(1)2](1)[(1)2]()()(1)[(1)2](1)[(1)2]m m m m j k j k k k j k j kk k k vn n n n i l i l lli l i l l lj T j j T j kG j j j T j j T j ωωωωωξωξωωωωωωωωωωωξωξωωωω+-+---=+-+---∏∏∏∏∏∏∏∏ （1）式中：分子多项式中最小相位环节的阶次和为111212m m m =+，分子多项式中非最小相位环节的阶次和为212222m m m =+， 分母多项式中最小相位环节的阶次和为111212n n n v =++， 分母多项式中非最小相位环节的阶次和为212222n n n =+，分子多项式阶次之和为12m m m =+，分母多项式阶次之和为12n n n =+。

注：式中仅包含教材p192所列5种非最小相位环节，不包含形如1Ts -、11Ts -、22121nns s ξωω+-、2221nns s ξωω+-等非最小相位环节。

2、求N 氏曲线的起点当ω→0＋时，（1）式可近似为：0lim ()()k vkG j j ωωω+→→（2）于是，N 氏曲线的起点取决于开环放大系数k 和系统的型v 。

① 当0v =时，N 氏曲线起始于实轴上的一点（k ，0）或（－k ，0）； ② 当0v >时，N 氏曲线起始于无穷远点：0k >时，沿着角度()2v πϕω=-⨯起始于无穷远点；0k <时，沿着角度()2v πϕωπ=--⨯起始于无穷远点。

③ 当0v <时，N 氏曲线起始于原点：0k >时，沿着角度()2v πϕω=⨯起始于原点；0k <时，沿着角度()2v πϕωπ=-+⨯起始于原点。

3、求N 氏曲线的终点当ω→＋∞时，（1）式中各环节的相角分别为：(1)j T ω+环节的相频特性：112T tg ωπ-→，(1)j T ω-环节的相频特性：1()()1()2Q T tg P ωπ---→-+， 22[(1)2]nnj ωωξωω-+环节的相频特性：11222122()()()11n n n nQ tg tg P ωξξωωπωωωωω--+=→---， 22[(1)2]n n j ωωξωω--环节的相频特性：11222122()()()11n n n nQ tg tg P ωξξωωπωωωωω-----=→----， 1()vj ω环节的相频特性：2v π-⨯，K 环节的相频特性：0, ()00,()k k ϕωϕωπ>→⎧⎨<→-⎩。

于是，当ω→＋∞时，① n m =，lim ()k G j k ωω→+∞→，N 氏曲线终止于实轴上的一点（k ，0）或（－k ，0）② n m >，N 氏曲线终止于原点；③ n m <，N 氏曲线终止于无穷远点。

其终点的相频特性为：1121122211211222121212121212()()()22()()2222 =2222[()()], 02 =[()()], 02k m m m m v n n n n k m m n n m m n n k m m n n k ππϕωππππππππππππππ=⨯+⨯+⨯-+⨯--⨯-⨯-⨯-⨯--⨯-⨯-⨯-⨯+⨯⎧---⨯>⎨---⨯-<的相角＋的相角＋⎪⎪⎩ （3)特殊地，当开环系统为最小相位系统时，有：0k >，122212220m m n n ====，则分子的阶次为111212m m m m ==+，分母的阶次为111212n n n n v ==++。

① n m =，N 氏曲线终止于实轴上的一点（k ，0）；② n m >，N 氏曲线沿着角度()()2n m πϕω=--⨯终止于原点；③ n m <，N 氏曲线沿着角度()()2m n πϕω=-⨯终止于无穷远点。

4、求ω：0＋→＋∞中的一些特色点：如N 氏曲线与实轴或虚轴的交点；极值点等等。

5、若开环系统存在等幅振荡环节，即开环频率特性（1）式中具有形如221(1)nωω-的因子时（无论最小相位系统还是非最小相位系统），N 氏曲线在ωn 处有无穷远间断点（A(ω)→∞），即N 氏曲线为由ω：0＋→ωn-和ω：ωn ＋→＋∞两段曲线所组成。

2221()(1)nG j ωωω=-环节在n ωω=处的相频特性为：1221221222(0)0()0()10lim ()(0)01()()1n n n n n n Q tg P tg Q tg P ωωωωϕωωπωωω---→-+⎧-=⎪+-⎪⎪=-=⎨⎪--=--⎪-⎪⎩设当n ωω=时，（1）式中除221(1)nωω-环节外，G 1(j ω)不含n j ωω=±的开环极点，也即：11111222122(), ()()()()()()[()], (1)(1)n n n k n n n nG j A G j G j G j ωωϕωωωωωϕωωωωϕωπωωωωωω→-+∞∠→⎧∠====⎨∞∠-→⎩-- （4）二、ω：－∞→0－因为幅频特性是关于ω的偶函数，而相频特性是关于ω的奇函数，所以ω：－∞→0－的幅相曲线与ω：0＋→＋∞的幅相曲线关于实轴成镜像对称。

三、ω： 0－→0＋对于（1）式，当ω→0－时，有：0lim ()()k vk G j j ωωω-→→- ① 当0v =时，N 氏曲线为实轴上的一点（k ，0）或（－k ，0）； ② 当0v >时，N 氏曲线起始于无穷远点：0k >时，沿着角度()2v πϕω=⨯起始于无穷远点；0k <时，沿着角度()2v πϕωπ=-+⨯起始于无穷远点。

③ 当0v <时，N 氏曲线起始于原点：0k >时，沿着角度()2v πϕω=-⨯起始于原点；0k <时，沿着角度()2v πϕωπ=--⨯起始于原点。

于是，对于（1）式系统：1、 当0v =，ω从0－→0＋的N 氏曲线为实轴上同一点（k ，0）或（－k ，0）；2、 当0v >，0k >时，ω从0－→0＋的N 氏曲线为半径为∞、角度从2v π⨯→2v π-⨯的1242v v ⨯=个圆。

0k <时，ω从0－→0＋的N 氏曲线为半径为∞、角度从2v ππ-+⨯→2v ππ--⨯的1242v v ⨯=个圆。

3、当0v <，0k >时，ω从0－→0＋的N 氏曲线分别沿角度2v π-⨯、2v π⨯趋于原点。

0k <时，ω从0－→0＋的N 氏曲线分别沿角度2v ππ--⨯、2v ππ-+⨯趋于原点。

(二) 已知系统开环传递函数G k (s )，绘制Bode 图（开环对数频率特性曲线） 一、迭加法1、由已知的G k (s )求()()k k s j G j G s ωω==，A (ω)，φ(ω)；()k G j ω如（1）式所示，()A ω= （4）11221111()20lg ()20lg 20lg m n j i m n k l L A k v ωωω======-⨯++∑∑∑∑ （5）1211211222112211221212112112112112111112211112211112111222()111122 2111k k m m m m jk j kj k j k k kl l n n n i l i li l i l T T k tg tg tg tg T T v tg tg tg tg ωωξξωωωωϕωωωωωωωξξωωωωπωω----====----===--=+++-----⨯-----∑∑∑∑∑∑∑的相角+222222121nl lωω=-∑ （6）2、在对数坐标上，先作出各基本因子对应的典型环节的对数幅频特性和相频特性；再逐点相加，即可得到系统的开环对数频率特性曲线。

二、实用法（以分段直线近似代替实际曲线）实际绘制Bode 曲线时，可不必分别画出各环节的特性曲线再相加，而是按以下步骤一次完成（用分段直线近似代替实际曲线） 1、 确定k 值，v 值和各个交接频率根据（1）式，将各转折频率（交接频率）：111j j T ω=， 1k ω， 221j j T ω=， 2k ω，111i i T ω=， 1l ω， 221i i T ω=， 2l ω按从小到大的顺序依次标注在频率轴上。

2、 绘制系统对数幅频特性的低频渐近线00()lim 20lg ()lim 20lg lim 20lg20lg 20lg ()vvk kL A k v j ωωωωωωωω→→→====-低 （7）（7）式为斜率等于20/vdB dec -⋅，过当1ω=、()20lg L k ω=一点（即过点（1，20k lg ））的直线方程； 或为斜率等于20/vdB dec -⋅，过()0L ω=低、1vk ω=一点（即过点（1vk ，0））的直线方程。

3、 以低频渐近线作为近似分段直线的第一段，从低频段开始，沿频率增大的方向，每遇到一个交接频率改变一次分段直线的斜率当遇到111j j T ω=、221j j T ω=时，斜率变化为dec dB /20+； 当遇到1k ω、2k ω时，斜率变化为dec dB /40+； 当遇到111i i T ω=、221i i Tω=时，斜率变化为dec dB /20-； 当遇到1l ω、2l ω时，斜率变化为dec dB /40-；依次绘出分段直线，即可获得系统开环对数幅频特性曲线的近似表示。

也可利用典型环节修正的方法对分段直线进行误差修正，得到准确的对数幅频特性曲线。

修正时应考虑相邻各环节的互相影响。

4、 分段直线的最后一段是开环对数幅频特性的高频渐近线斜率为：dec dB m n /)(20--；该斜率用来验证1～3步绘制曲线的正确与否。

5、 对数相频特性也可利用典型环节的各对数相频特性曲线相加得到；或者直接利用相频特性表达式（6）进行计算。

（三）已知系统的Bode 图（开环对数频率特性曲线），求系统开环传递函数 1. 假设系统为最小相位系统。

2. 根据已知的对数幅频特性曲线（或其渐近线），确定其传递函数。

121222112211(1)(12)()()(1)(12)m m j k j k k k n n v i l i l l l k j T j G j j j T j ωωωξωωωωωωωξωω====+-+=+-+∏∏∏∏，12122221122211(1)(21)()(1)(21)m mj k j k kk n n vi l i l l lk T s s s G s s T s s s ωωξωωωωξωω====+++=+++∏∏∏∏ 式中各环节转折频率及相应的时间常数等参数可从已知的对数幅频特性曲线（渐近线）上直接确定，而系统的型v 和开环放大系数k 均由对数幅频特性曲线的低频段来确定：()lim 20lglim 20lg20lg 20lg ()vvk kL k v j ωωωωωω→→===-低① 如果开环对数幅频特性曲线的低频段是平行于ω轴的水平线（如下图），则系统为0型系统（0v =）kl g 20设水平线高度为x , 则20lg 020lg x k ω=-*，可确定开环放大系数2010xk =② 如果开环对数幅频特性曲线的低频段是斜率为20/dB dec -的直线，则系统为1型系统（1v =）vk lg 20decdB /20-1=w vk w =()20lg 20lg L k ωω=-低a. 设开环对数幅频特性曲线的低频渐近线或其延长线与dB 0线交点的频率为c ω， 则c k ω=，（此时()0,20lg 20lg c c L k ωω==）b. 设开环对数幅频特性曲线的低频渐近线或其延长线与1ω=垂直线交点上的幅值为x ,则2010xk =（此时(1),20lg 20lg120lg L x x k k ==-=）③ 如果开环对数幅频特性曲线的低频段是斜率为40/dB dec -的直线，则系统为2型系统（2v =）()20lg 40lg L k ωω=-低1=w decdB /40-αk lg 20αkw c =a. c ω， 则2c k ω=，（此时()0,20lg 40lg c c L k ωω==）b. 设开环对数幅频特性曲线的低频渐近线或其延长线与1ω=垂直线交点上的幅值为x ,则2010xk =（此时(1),20lg 40lg120lg L x x k k ==-=）3. 求出相频特性的表达式，并作出相频特性曲线。