开环概略幅相曲线绘制

开环系统频率特性曲线的绘制方法（一) 已知系统开环传递函数G k （s )，绘制Nyquist 曲线(开环幅相曲线) 一、ω：0＋→＋∞1、由已知的G k (s ）求()()k k s j G j G s ωω==，A (ω），φ(ω） ，P (ω），Q (ω）;112112221122121122121121122211221211221222222222(1)[(1)2](1)[(1)2]()()(1)[(1)2](1)[(1)2]m m m m j k j kk k j k j kk k k vn n n n i l i l lli l i l l lj T j j T j k G j j j T j j T j ωωωωωξωξωωωωωωωωωωωξωξωωωω+-+---=+-+---∏∏∏∏∏∏∏∏ （1）式中:分子多项式中最小相位环节的阶次和为111212m m m =+，分子多项式中非最小相位环节的阶次和为212222m m m =+， 分母多项式中最小相位环节的阶次和为111212n n n v =++， 分母多项式中非最小相位环节的阶次和为212222n n n =+,分子多项式阶次之和为12m m m =+，分母多项式阶次之和为12n n n =+。

注:式中仅包含教材p192所列5种非最小相位环节,不包含形如1Ts -、11Ts -、22121nns s ξωω+-、2221nns s ξωω+-等非最小相位环节。

2、求N 氏曲线的起点当ω→0＋时，（1）式可近似为：0lim ()()k vk G j j ωωω+→→（2）于是，N 氏曲线的起点取决于开环放大系数k 和系统的型v 。

① 当0v =时，N 氏曲线起始于实轴上的一点(k ，0)或（－k ，0）； ② 当0v >时，N 氏曲线起始于无穷远点：0k >时，沿着角度()2v πϕω=-⨯起始于无穷远点;0k <时,沿着角度()2v πϕωπ=--⨯起始于无穷远点。

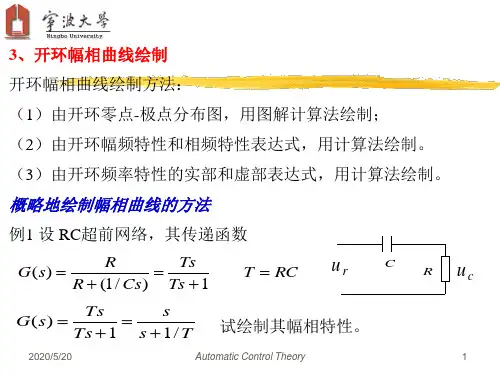
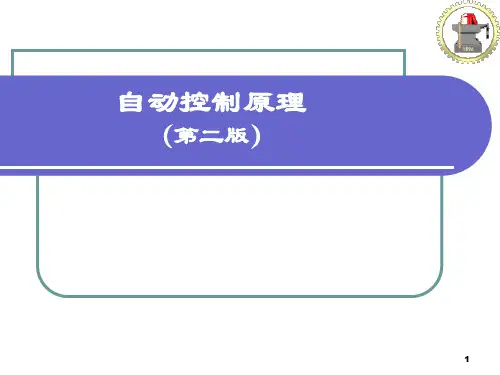
开环幅相频率特性曲线和对数相频特性曲线的完整画法一般情况下，以X轴为频率，Y轴为幅度和相位，将开环幅相特性曲
线画成两条曲线，分别为幅度特性曲线和相位特性曲线。

1.幅度特性曲线：以频率（角频率）为X轴，以幅度为Y轴，表示系
统输出信号与输入信号之间的幅度比值或增益。

曲线上沿频率增加时，增
益也会增大，但是增大的幅度会减小，因此，在此曲线上，增益逐渐降低，形成一个弓形曲线。

2.相位特性曲线：以频率（角频率）为X轴，以相位为Y轴，表示系
统输出信号与输入信号之间的相位差。

曲线上沿频率增加时，相位差也会
逐渐增大，相位曲线与幅度曲线的关系是一种折线图，但相位差的增加是
随着频率的函数变化。

对数相频特性曲线:
以对数频率（角对数频率）为X轴，以幅度为Y轴，表示系统输出信
号与输入信号之间的幅度比值或增益。

曲线上沿频率增加时，增益也会增大，但是增大的幅度会减小，因此，在此曲线上，增益也会逐渐减小，形
成一个弓形曲线。

2V 开环系统幅相曲线的绘制（奈奎斯特曲线）V 开环系统对数坐标频率特性的绘制（波德图）V 最小相位系统V由波德图求传递函数学习思路：1、三频段法：低频段、中频段和高频段；确定起点与终点计算特殊点，如转折点与交接频率点关键区的选点运算，逐点描迹法2、定性分析(趋势分析)主要内容3、中频段的绘制(1)特殊点的绘制：如虚轴交点，实轴交点，转折点系统幅相特性曲线与负实轴的交点坐标是判定系统稳定的关键因素，而与实轴的交点可用于确定中频段的位置，中频段的形状主要由频率特性的分子、分母中各因子的时间常数决定。

(2)逐点描迹法: 复杂区间，特殊区域1415求出ω，代入实部Re[G(j ω)H(j ω)］中，可得幅相曲线与实轴的交点坐标。

（2）曲线与虚轴交点坐标的求取同理令Re[G(j ω)H(j ω)]=0 ，求得ω代入虚部可确定曲线与虚轴的交点坐标（3）列表计算一些中、高频段的频率点坐标（4）逐点描绘幅相特性曲线（1）曲线与实轴交点坐标的求取令虚部为零，即Im[G(j )H(j )]0G(j )H(j )(2k 1)k 0,1,2ωωωωπ=∠=+=±±"根据特殊点的绘制：nyquist([5 1],[2 1]) nyquist([-5 1],[2 1])101 10四、由频率特性曲线求系统传递函数根据最小相位系统的特点，即系统的对数幅频特性和对数相频特性有相同的变化趋势，我们可根据系统地对数幅频特性求系统的开环传递函数。

步骤如下：¾对数幅频特性的低频段的斜率和高度可确定积分环节的个数和比例值K；¾从低频到高频对数幅频特性的斜率变化和转折频率的大小可确定应加的环节。

311ϕ+°90() G slgω1)s+1(1)0.8s+K41小结作业：5-5(2),5-6(3)☻开环系统幅相曲线的绘制（绘制奈氏图）☻开环系统对数坐标频率特性的绘制（绘制波德图）及由图推导传递函数☻最小相位系统敬请提出宝贵意见前向通路反馈通路记住这个结构，并用于思维。

5.3 系统开环频率特性的绘制对自动控制系统进行频域分析时，通常是根据开环系统的频率特性来判断闭环系统的稳定性和 估算闭环系统时域响应的各项性能指标，或者根据开环系统的频率特性绘制闭环系统的频率特性， 然后再分析及估算时域性能指标。

因此，掌握开环系统的频率特性曲线的绘制和特点是十分重要的。

5.3.1 开环幅相曲线的绘制开环系统的幅相频率特性曲线简称为开环幅相曲线。

准确的开环幅相曲线可以根据系统的开环 幅频特性和相频特性的表达式，用解析计算法绘制。

显然，这种方法比较麻烦。

在一般情况下，只 需要绘制概略开环幅相曲线，概略开环幅相曲线的绘制方法比较简单，但是概略曲线应保持准确曲 线的重要特征，并且在要研究的点附近有足够的准确性。

下面首先介绍幅相频率特性曲线的一般规律与特点， 然后举例说明概略绘制开环幅相曲线的方 法。

设系统开环传递函数的一般形式为式中，K 为开环增益；v 为系统中积分环节的个数。

则系统的开环频率特性为mK (j i 1)G(j )H(j ) 七(5-50)(j )v (j T j 1)j 11.开环幅相曲线的起点 在低频段当0时，由式(5-50)可得由式(5-51)可知，当0时，开环幅相曲线的起点取决于开环传递函数中积分环节的个数v 和开环增益K ，参见图5-23 (a )。

0型(v =0)系统，开环幅相曲线起始于实轴上的 (K, j0)点。

1型(v =1)系统，开环幅相曲线起始于相角为90的无穷远处。

当于与虚轴的平行的直线，其横坐标G(s)H(s)K ( i S 1)i 1 n vs v(T j S 1)j 1(n m)(5-49)lim 0G(j )H(j ))vlimeJ( v90)(5-51)0时，曲线渐近图5-23不同类型系统的幅相频率特性即开环幅相曲线以(n m) 90方向终止于坐标原点，如图5-23 (b )所示。

3.开环幅相曲线与实轴的交点 开环幅相曲线与实轴的交点频率X 可由下式求出，即令式(5-50)的虚部为零Im G(j )H(j )(5-54)将求出的交点频率x 代入式(5-50)的实部，即ReG( j x )H (j x )(5-55)由式(5-55)可计算出开环幅相曲线与实轴的交点坐标值。

掌握这三“点”，绘制幅相频率特性曲线图soesay！大家好，我是宝刀君，很高兴，我们又见面了~如题，众所周知，幅相频率特性曲线图又叫奈奎斯特曲线、奈氏曲线、幅相特性，有些参考书上也叫极坐标图。

不管说哪个，只要是提到绘制这些概念的，意思就是让你绘制下面形状的图：在正式讲解幅相特性曲线图怎么画之前，我个人觉得有些基础知识点需要你在头脑中有个概念，回忆起当年学习自控时，好多人一时半会儿摸不到门的原因是对基本的概念不清。

基础知识点1复数的幅值和相角的计算、共轭复数复数这个知识点其实是复变函数里面讲的，就是说我们平时见到的任意一个数，其实都可以写成实部+虚部的形式，平时我们见到的大部分数都是实数。

百度百科的解释：复数的模的计算：根号下实部的平方加虚部的平方。

共轭复数就是实部一样，虚部互为相反数的复数。

一个复数和它的共轭复数相乘，产生的结果就变成实数了，有点像数学公式里的平方差公式，因为 i 的平方等于 -1 嘛，所以第二项就为正的了。

除了以上概念，我们还要明白：复数的实部、虚部与它的模值、角度之间的关系式。

由上面的公式可以看出，实部是模值与余弦函数相乘得到的，假如这个角度为0，那么这个复数整体就只有实部，就是我们常见的实数。

而如果角度为90度，那么就只有虚部。

或许有同学会问，那这个角度怎么求啊？给你一个复数，虚部除以实部就是这个角度的正切函数啊！所以你只需要一个灵巧的计算器计算下它的反正切就知道角度了呢~ 因此，如果知道了模值、角度，我们就可以很轻松的写出这个复数的指数形式。

基础知识点2开环传递函数的幅值和相角的计算明白了上面有关复数的概念，接下来我们谈谈频率域中的开环传递函数 G(jw) 的模值和角度的计算，如下图所示：计算模值时，把每一个小环节的模值表达式写出来，然后依次序乘在一起即可。

相角呢，角度怎么计算？还是之前说的，整体的角度等于分子的角度减去分母的角度，这个在之前发的文章[深度]详解根轨迹的8大规则中讲解的如何巧妙计算起始角和终止角的思路一致，都是分子角-分母角、或者叫零点角-极点角（我自创的刀法，我自己经常这样叫，现在传授给你）哈哈哈，这样叫是不是很有意思啊~就像有些学生做不定积分/定积分时，看到那个不定积分的符号，长得像S，做题之前都要先大喊一声：Shit！当然，你也可以用另外一个方法计算：借助于上下同乘以各个环节的共轭复数，这样就把分母化简成一个实数，把分子化简成了具有一个实部和一个虚部的复数形式，此时， G(jw) 整体就变成了一个复数，这时利用定义计算其模值和相角也可以。