概略幅相曲线例题

控制工程基础习题答案第一章1-1 试比较开环控制系统和闭环控制系统的优缺点？（略）1-2 日常生活中有许多闭环和开环控制系统。

试举几个具体例子，并说明它们的工作原理，画出结构方框图。

（略）1-3 图1.14是液面自动控制系统的两种原理示意图。

在运行中，希望液面高度H 0维持不变。

1．试说明各系统的工作原理。

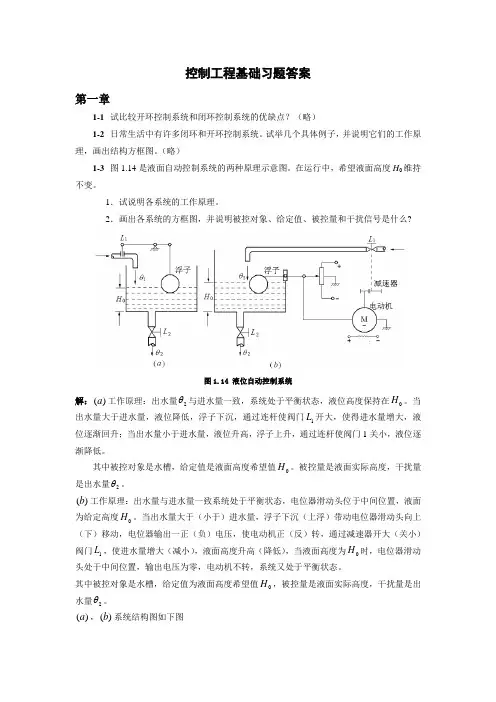
2．画出各系统的方框图，并说明被控对象、给定值、被控量和干扰信号是什么?图1.14 液位自动控制系统解：()a 工作原理：出水量2θ与进水量一致，系统处于平衡状态，液位高度保持在0H 。

当出水量大于进水量，液位降低，浮子下沉，通过连杆使阀门1L 开大，使得进水量增大，液位逐渐回升；当出水量小于进水量，液位升高，浮子上升，通过连杆使阀门1关小，液位逐渐降低。

其中被控对象是水槽，给定值是液面高度希望值0H 。

被控量是液面实际高度，干扰量是出水量2θ。

()b 工作原理：出水量与进水量一致系统处于平衡状态，电位器滑动头位于中间位置，液面为给定高度0H 。

当出水量大于（小于）进水量，浮子下沉（上浮）带动电位器滑动头向上（下）移动，电位器输出一正（负）电压，使电动机正（反）转，通过减速器开大（关小）阀门1L ，使进水量增大（减小），液面高度升高（降低），当液面高度为0H 时，电位器滑动头处于中间位置，输出电压为零，电动机不转，系统又处于平衡状态。

其中被控对象是水槽，给定值为液面高度希望值0H ，被控量是液面实际高度，干扰量是出水量2θ。

()a ，()b 系统结构图如下图1-4 若将图1.14(a )系统结构改为图1.15。

试说明其工作原理。

并与图1.14(a )比较有何不同?对系统工作有何影响?解：若将1-17()a 系统结构图改为1-18，系统变成了正反馈，当出水量与进水量一致，液面高度为给定值0H 。

当出水量大于进水量，液面位降低，浮子下称，通过连杆使阀门1关小，进水量越来越小，液面高度不能保持给定高度0H ，同样当出水量小于进水量，浮子上浮，液位升高，使阀门1开大，进水量增大，液位越来越高，不可能维持在给定高度0H1-5 图1.16是控制导弹发射架方位的电位器式随动系统原理图。

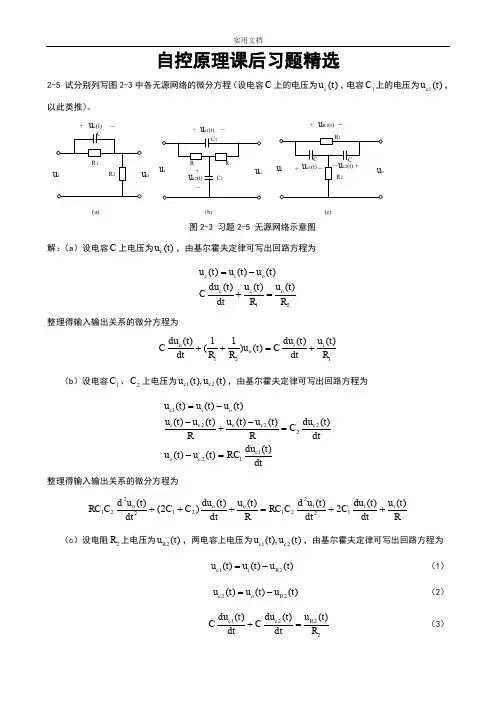
自控原理课后习题精选2-5 试分别列写图2-3中各无源网络的微分方程（设电容C 上的电压为)(t u c ，电容1C 上的电压为)(1t u c ，以此类推）。

o(a)+－u c (t)(b)+－u c1(t)(c)+－u R1(t)图2-3 习题2-5 无源网络示意图解：（a ）设电容C 上电压为)(t u c ，由基尔霍夫定律可写出回路方程为21)()()()()()(R t u R t u dt t du Ct u t u t u o c c o i c =+-=整理得输入输出关系的微分方程为121)()()()11()(R t u dt t du C t u R R dt t du Ci i o o +=++ （b ）设电容1C 、2C 上电压为)(),(21t u t u c c ，由基尔霍夫定律可写出回路方程为dtt du RC t u t u dtt du C R t u t u R t u t u t u t u t u c c o c c o c i o i c )()()()()()()()()()()(11222221=-=-+--=整理得输入输出关系的微分方程为Rt u dt t du C dt t u d C RC R t u dt t du C C dt t u d C RC i i i o o o )()(2)()()()2()(12221212221++=+++ （c ）设电阻2R 上电压为2()R u t ，两电容上电压为)(),(21t u t u c c ，由基尔霍夫定律可写出回路方程为)()()(21t u t u t u R i c -= （1） )()()(22t u t u t u R o c -= （2）2221)()()(R t u dt t du C dt t du CR c c =+ （3）dtt du C R t u t u c o i )()()(21=- （4）（2）代入（4）并整理得CR t u t u dt t du dt t du o i o R 12)()()()(--= （5） （1）、（2）代入（3）并整理得222)()(2)()(R t u dt t du C dt t du C dt t du CR R o i =-+ 两端取微分，并将（5）代入，整理得输入输出关系的微分方程为CR t u dt t du C R dt t u d C R C R t u dt t du C R dt t u d C R i i i o o o 1122211222)()(1)()()()11()(++=+++2-6 求图2-4中各无源网络的传递函数。

第三章3－3 已知各系统的脉冲响应，试求系统的闭环传递函数()s Φ：()()1.253(1)()0.0125;(2)()510sin 445;(3)()0.11t t k t e k t t t k t e --==++=-解答： （1） []0.0125()() 1.25s L k t s Φ==+（2）[])222223222()()5sin 4cos 454441511616116s L k t L t t t s s s s s s s s ⎡⎤Φ==++⎢⎥⎣⎦⎫=++⎪++⎭⎛⎫+++ ⎪⎝⎭=⎛⎫+ ⎪⎝⎭（3）[]()111()()0.1110313s L k t s s s s ⎡⎤⎢⎥Φ==-=⎢⎥+⎢⎥+⎣⎦ 3-4 已知二阶系统的单位阶跃响应为)6.1sin(5.1210)(1.532.1︒-+-=t t h et试求系统的超调量σ%，峰值时间tp和调节时间ts.解答：因为0<ξ<1，所以系统是欠阻尼状态。

阻尼比ξ=cos(1.53︒)=0.6，自然频率26.0/2.1==w n，阻尼振荡频率w d=6.16.01212=-⨯=-=ξww nd1． 峰值时间tp的计算96.16.1===ππwt dp2． 调节时间ts的计算9.226.05.35.3=⨯==w t ns ξ3． 超调量σ%的计算%48.9%1006.0%100%221/6.01/=⨯=⨯=-⨯---eeππξξσ3-5设单位反馈系统的开环传递函数为)6.0(14.0)(++=s s s s G ，试求系统在单位阶跃输入下的动态性能。

解答：方法一：根据比例-微分一节推导出的公式)135(6.014.0)12/()1()(+⨯⨯+=++=s s s s s s K s G w T n d ξ1)5.2(4.0114.0)6.0(14.01)6.0(14.0)2()(1)()(22222+++=+++=+++++=+++=+=s s s s s s s s s s s zs z S G s G s s s w w s w nn dn ξφ)1()](1[12)1sin(1)(222222ξξξξξξξπψξddnddndnn ddn t arctg z arctg z r t w r t h ww w w zw e nd-+--+-=-+-=ψ+-+=-把z=1/Td=2.5,1=wn,5.0=ξd代入可得)3.8323sin(5.005.11)7.9623sin(5.005.11)( ---=--+=t e t t e t t h峰值时间的计算0472.1)1(2=-=ξξβdddarctg ，-1.6877=ψ158.312=--=ξβψdndpwt超调量得计算%65.21%10011%22=⨯--=-ξξξσddetrpd调节时间得计算29.6)ln(21ln )2ln(2131222=--+-+=-ww w z t ndn n d sd z ξξξ方法二：根据基本定义来求解闭环传递函数为114.0)6.0(14.01)6.0(14.0)(1)()(2+++=+++++=+=s s s s s s s s S G s G s s φ当输入为单位阶跃函数时)232()21(21.0)232()21(2)21(116.01)1(14.0)(22++-++++-+=++--+=+++=s s s s s s s s s s s C s s 得单位阶跃响应)23sin(1.0)23cos(1)(2121t t t h e et --⨯--=)3.8423sin(121+-=-t et )0(≥t 1． 峰值时间tp的计算 对h(t)求导并令其等于零得-0.5023)23cos()23sin(3.843.842121=⨯+-+︒-︒-t e t ep p t t p p3)23tan(3.84=+︒t pt p =2.9 2.超调量σ%的计算 %100)()()(%⨯∞∞-=h h h t p σ=17.49%3. 调节时间ts得计算05.0)84.523sin(21≤-⨯-t est s 5.33=t s3-6.已知控制系统的单位阶跃响应为 6010()10.2 1.2t th t e e --=+- ，试确定系统的阻尼比ζ和自然频率n ω。

第五章 频域响应法5-1 频率特性一． 频率特性的基本概念1. 所谓频率特性，即在零初始条件下，系统输入在正弦信号的控制下，其稳态输出C(t) 的被控制量信号的幅值A(ω)和相角ψ（ω）随r(t)信号的角频率ω变化的规律，记为G(j ω)。

G(j ω)=G(S)| s=j ω C(j ω) C(s)G(j ω)== R(j ω) R(s)| s=j ωb 0(j ω) m +b 1(j ω) 1+m +……+b 1-m (j ω)+b m G(j ω)=( j ω) n +a 1(j ω) 1-n +……a 1-n (j ω)+a n2、G(j ω)的数模表达式有两种标准式: （1）Nyquist 标准式：G(j ω)=︱G(j ω)︱e)(jw G j ∠=u(ω)+jv(ω)其中A(j ω)= ︱G(j ω)︱称为幅频特性，是ω的偶函数。

ψ(ω)= ∠G(j ω) 称为相频特性，是ω的奇函数。

u(ω)=Re [G(j ω)]为实部； v(ω)=Im [G(j ω)]为虚部。

（2）Bode 表达式：L (ω)=20lg [A(j ω) ] 称为对数幅频，ψ(ω)= ∠G(j ω) 称为对数相频。

二． 频率特性的图解表示法在工程分析和设计中，通常把频率特性画成曲线，从这些频率特性曲线出发研究。

现以RC 网络为例。

如图5-2。

其频率特性为G(j ω)=)(11jw T +（T=RC ）。

A(ω)= G(j ω)=2)(11TW +；ψ(ω)=-arctg(T ω)1.极坐标图----Nyquist图当ω=0→∞变化时,A(ω)和φ(ω)随ω而变,以A(ω)作幅值,φ(ω)作相角的端点在s平面上形成的轨迹,称Nyquist曲线（幅相频率特性曲线）简称幅相曲线即Nyquist图，是频率响应法中常用的一种曲线。

2、对数坐标图----Bode图对数频率特性曲线又称Bode曲线，包括对数幅频和对数相频两条曲线。

自动控制原理试-4(总分：100.00，做题时间：90分钟)一、(总题数：29，分数：100.00)1.已知某系统结构图如图所示，试根据频率特性物理意义，求当信号输入为r(t)=2sin(t+30°)+cos(2t-45°)时，系统的稳态输出c ss和稳态误差e ss。

（分数：2.00）__________________________________________________________________________________________ 正确答案：()解析：闭环传递函数；频率特性；；误差传递函数；误差频率特性；；当r 1(t)=2sin(t+30°)时，当r 2 (t)=cos(2t-45°)时，因此在输入作用下，2.最小相位系统对数幅频渐近特性如图所示，请确定系统的传递函数。

（分数：2.00）__________________________________________________________________________________________ 正确答案：()解析：由图知在低频段渐近线斜率为0，因为最小交接频率前的低频段L(ω)=-v20lgω，故v=0。

渐近特性为分段线性函数，在各交接频率处，渐近特性斜率发生变化。

在ω=0.1处斜率变化20dB/dec，属一阶微分环节。

在ω=ω1处斜率变化-20dB/dec，属惯性环节。

在ω=ω2处斜率变化-20dB/dec，属惯性环节。

在ω=ω3处斜率变化-20dB/dec，属惯性环节。

在ω=ω4处斜率变化-20dB/dec，属惯性环节。

因此，系统的传递函数具有下述形式式中，K，ω1，ω2，ω3，ω4待定。

由201gK=30得K=10 1.5≈31.62。

因渐近线直线段，若设某段的斜率为k，(ωA，L(ωA ))，(ωB，L(ωB ))为该线段上的两点，则由直线方程：确定所以确定，所以确定，所以确定，所以于是，所求的传递函数为单位反馈控制系统的开环传递函数为：（分数：4.00）(1).求系统的幅值裕量为20dB时的K值。

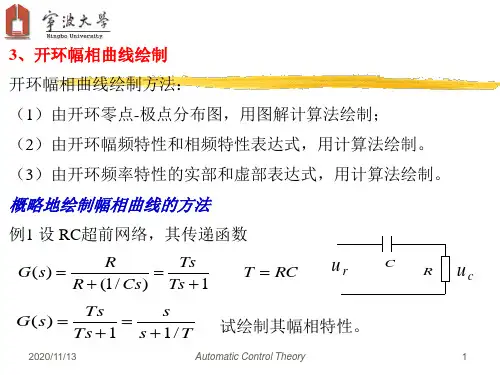
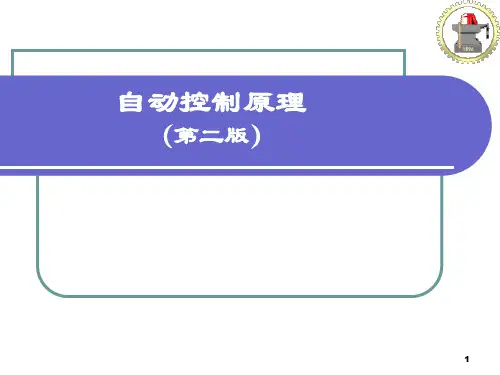
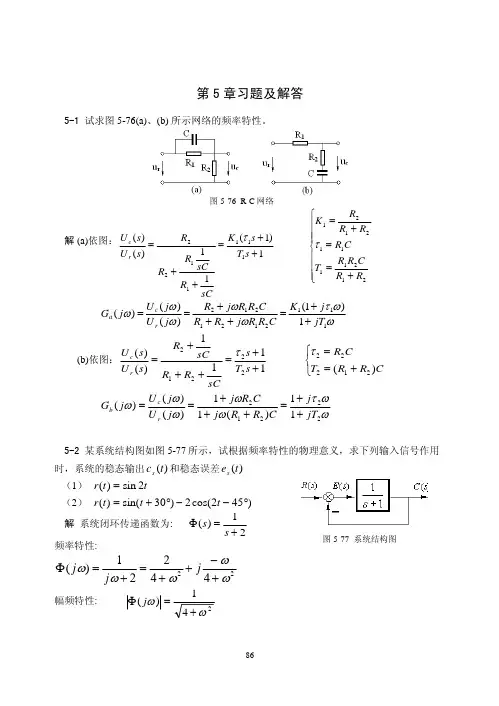
第5章习题及解答5-1 试求图5-76(a)、(b) 所示网络的频率特性。

图5-76 R-C 网络解 (a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R R R R K s T s K sCR sC R R R s U s U r c ττ ωωτωωωωω11121212121)1()()()(jT j K C R R j R R C R R j R j U j U j G r c a ++=+++==(b)依图：⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sCR s U s U r c)(1111)()(2122222212ττ ωωτωωωωω2221211)(11)()()(jT j C R R j C R j j U j U j G r c b ++=+++==5-2 某系统结构图如图5-77所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出和稳态误差 )(t c s )(t e s图5-77 系统结构图（1）t t r 2sin )(= （2） )452cos(2)30sin()(°−−°+=t t t r 解 系统闭环传递函数为: 21)(+=Φs s 频率特性:2244221)(ωωωωω+−++=+=Φjj j幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωϕ= 系统误差传递函数: ,21)(11)(++=+=Φs s s G s e则 2arctan(arctan )(,41)(22ωωωϕωωω−=++=Φj j e e（1）当时, t t r 2sin )(=2=ω，r m =1则 ,35.081)(2==Φ=ωωj o 45)22arctan()2(−=−=j ϕo4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2()(o−=+Φ=t t j r t c m s ϕ)4.182sin(79.0)2sin()2()(o+=+Φ=t t j r t e e e m s ϕ （2） 当 )452cos(2)30sin()(°−−°+=t t t r 时:⎩⎨⎧====2,21,12211m m r r ωω o 5.26)21arctan()1(45.055)1(−=−===Φj j ϕ o 4.1831arctan()1(63.0510)1(====Φj j e e ϕ)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m s ϕϕ+−⋅Φ−++⋅Φ=oo)902cos(7.0)4.3sin(4.0oo−−+=t t )]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m s ϕϕ+−⋅Φ−++⋅Φ=oo )6.262cos(58.1)4.48sin(63.0oo−−+=t t 5-3 若系统单位阶跃响应h t e e t t t()..=−+≥−−11808049试求系统频率特性。