运动界面追踪和重构方法的数值模拟

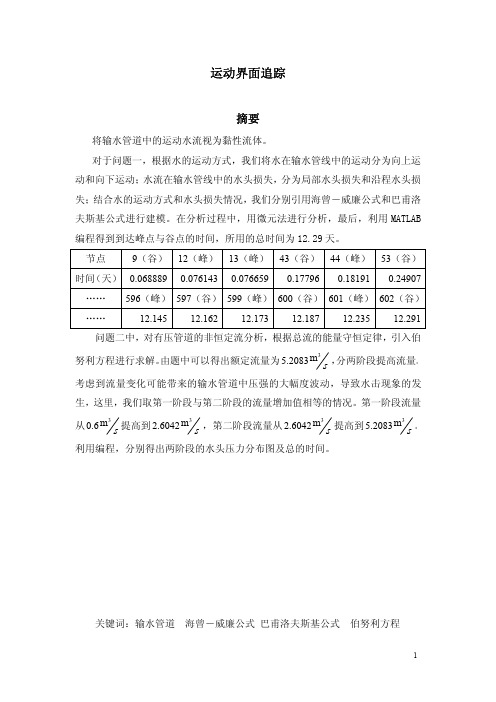
运动界面追踪摘要将输水管道中的运动水流视为黏性流体。

对于问题一，根据水的运动方式，我们将水在输水管线中的运动分为向上运动和向下运动；水流在输水管线中的水头损失，分为局部水头损失和沿程水头损失；结合水的运动方式和水头损失情况，我们分别引用海曾－威廉公式和巴甫洛夫斯基公式进行建模。

在分析过程中，用微元法进行分析，最后，利用MATLAB 编程得到到达峰点与谷点的时间，所用的总时间为12.29天。

节点9（谷）12（峰）13（峰）43（谷）44（峰）53（谷）时间（天）0.0688890.0761430.0766590.177960.181910.24907……596（峰）597（谷）599（峰）600（谷）601（峰）602（谷）……12.14512.16212.17312.18712.23512.291问题二中，对有压管道的非恒定流分析，根据总流的能量守恒定律，引入伯努利方程进行求解。

由题中可以得出额定流量为3m5.2083s，分两阶段提高流量。

考虑到流量变化可能带来的输水管道中压强的大幅度波动，导致水击现象的发生，这里，我们取第一阶段与第二阶段的流量增加值相等的情况。

第一阶段流量从3m 0.6s 提高到3m 2.6042s ，第二阶段流量从3m 2.6042s 提高到3m 5.2083s。

利用编程，分别得出两阶段的水头压力分布图及总的时间。

关键词：输水管道海曾－威廉公式巴甫洛夫斯基公式伯努利方程一：问题重述某输水管线是利用114米地面落差有压、重力流输水工程。

管径2.2米，管线长度176公里，地面高程变化很大。

当输水管线建成后，首次通水时，为了防止水流速波动产生水击破坏管线，只能以每秒0.6立方米的流速由某水库向管线内灌水。

当被供水城市水厂出流稳定后，再逐步提高入流速度达到每天45万吨（一期工程单线）的额定工作状态。

运动界面追踪问题：1．第一阶段：假设以每秒Q（=0.6）立方米入流速度向管线内灌水，模拟出水头前沿面的运动过程，计算出水头前沿面顺序到达管线高程谷点和峰点的时间。

三维气泡运动的数值模拟唐永刚【摘要】文章基于VOF模型,借助FLUENT软件,对单个三维气泡在近自由面运动进行了数值模拟.采用了VOF的PLIC界面重构方法,追踪气泡运动过程中气泡表面的变化.监测了气泡上升速度变化以及气泡运动对自由液面的影响.通过对直径不同的气泡数值模拟,得出了气泡运动的一些基本规律.本文数值模拟结果与实验值对比分析,三维数值模拟数据与试验结果吻合较好.【期刊名称】《南通航运职业技术学院学报》【年(卷),期】2011(010)003【总页数】6页(P37-41,91)【关键词】三维气泡;自由液面;数值模拟;VOF【作者】唐永刚【作者单位】江苏联合职业技术学院无锡交通分院,江苏无锡214151【正文语种】中文【中图分类】O3530 引言气泡运动广泛存在于船舶与海洋工程实际中，如船舶在航行中由于螺旋桨空化以及波浪翻卷与破碎产生气泡；水下爆炸产生空泡。

因此气泡动力学研究在船舶领域有较大的意义。

气泡在流体中运动是强非线性的，运动时界面变形较大，因此气泡运动数值模拟越来越受国内外学者的关注，而气泡运动界面追踪是研究重点。

气泡界面追踪方法有多种，目前比较常见界面追踪方法有边界积分法、VOF（流体体积）法、Level Set法、Lattice–Boltzmann法、Front Tracking法等。

[1-12]针对于高压爆炸产生的气泡运动规律分析，宗智、何亮、张恩国等人基于势流理论采用了边界积分法求解拉普拉斯方程，模拟了爆炸气泡运动规律。

吴锤洁、李霞采用了VOF中PLIC界面重构方法分析气泡与自由表面相互作用。

[13]Luz Amaya-Bower、Taehun Lee采用Lattice–Boltzmann法数值模拟了三维气泡运动，分析了气泡运动特性。

[14]本文基于VOF（流体体积）技术中的PLIC界面重构方法，对单个三维气泡在水中的运动进行了数值模拟，追踪了气泡界面变化和气泡在上升过程中的速度变化。

运动界面追踪问题—详细公式推导过程任务三运动界面追踪问题摘要关于运动界面追踪问题专业性很强，运用到很多水力学的理论公式，我们结合专业知识和生活实际解决两个问题。

问题一首先，我们将输水管送水模型分为跌水模型和灌水模型两大类。

采用局部分析方法针对输水管的两种状态采用微元法进行分析。

从而建立微分方程，精确地模拟出流体运动过程的模型。

对于跌水模型，我们建立了微分方程模型，模拟出水流下降过程，计算水流断面的速度和下降时间。

对于灌水模型，分别讨论前一峰点比后面的高和前一峰点比后面的低这两类情形，利用MA TLAB 计算出水流到达每一谷点和峰点的时间如表5.1和表5.2所示。

计算结果为水流到达终点（节点602）需要12.04天。

问题二我们在对有压管道非恒定流分析的基础上建立了水流的运动方程和连续方程，并利用特征线的计算方法将偏微分方程转化为常微分方程，然后对特征线方程组进行差分变换，配合初边值条件，编程求解输水管线全程的水头压力分布和从一种恒定流到另一种恒定流的时间。

当入流速度达到每天45万吨的额定状态后，在计算出水头损失的情况下运用不可压缩实际液体恒定流的能量方程（伯努利方程）求出管线水头压强分布，进而求出压力分布，最后利用有压管道水力过渡过程的连续方程的简化形式计算出所需时间。

最后利用MATLAB 计算出过渡所需时间130820t s ，约为36小时。

关键词运动界面追踪水力学连续方程运动方程能量方程非恒定流的基本方程组特征线方程有限差分方程偏微分方程1 问题重述某输水管线是利用114米地面落差有压、重力流输水工程。

管径2.2米，管线长度176公里，地面高程变化很大。

当输水管线建成后，首次通水时，为了防止水流速波动产生水击破坏管线，只能以每秒0.6立方米的流速由某水库向管线内灌水。

当被供水城市水厂出流稳定后，再逐步提高入流速度达到每天45万吨（一期工程单线）的额定工作状态。

需要解决的问题：（一）第一阶段：假设以每秒Q （=0.6）立方米入流速度向管线内灌水，模拟出水头前沿面的运动过程，计算出水头前沿面顺序到达管线高程谷点和峰点的时间。

一种精确求解两相流动的界面追踪方法孙东亮;王丽;徐进良【期刊名称】《科技信息》【年(卷),期】2011(000)016【摘要】本文提出了一种求解两相流动问题的精确稳定的界面追踪方法-ADV-VOF(accurate density and viscosity volume of fluid method).该方法具有以下特征:(1)基于同位网格系统;(2)使用PLIC方法捕捉界面和计算网格边界上精确的密度和粘度值;(3)采用守恒的Navier-scokes方程,其中对流项离散格式为有界高阶组合格式--STOIC;(4)应用分步算法求解守恒的Naviel-Stokes方程;(5)利用Bi-CGSTAB方法求解压力修正方程.以上特征保证了ADV-VOF方法是一种精确、稳定、高效、简便的界面追踪方法.最后我们对ADV-VOF方法和传统的IDV-VOF(inaccurate demity and viscosity volume of fluid method)方法进行了比较分析,得出ADV-VOF方法的性能远远优于传统的IDV-VOF方法.【总页数】2页(P30-31)【作者】孙东亮;王丽;徐进良【作者单位】华北电力大学新能源电力系统国家重点实验室、能源的安全与清洁利用北京市重点实验室及低品位能源多相流与传热北京市重点实验室;华北电力大学新能源电力系统国家重点实验室、能源的安全与清洁利用北京市重点实验室及低品位能源多相流与传热北京市重点实验室;华北电力大学新能源电力系统国家重点实验室、能源的安全与清洁利用北京市重点实验室及低品位能源多相流与传热北京市重点实验室【正文语种】中文【相关文献】1.亚网格内两相流动界面位置的精确定位算法2.一种任意界面的逐段迭代谢线追踪方法3.一种基于Boltzmann方程的碳基复合材料氧化烧蚀微观界面的追踪方法4.一种自由界面追踪的模板化VOF方法5.一种追踪多介质流体界面运动的NND数值模拟方法因版权原因，仅展示原文概要，查看原文内容请购买。

多相流体力学中的界面跟踪方法界面跟踪方法主要分为两大类：欧拉法和拉格朗日法。

欧拉法是基于空间网格的方法，它使得计算网格上的界面变得困难，特别是在复杂的流动情况下。

拉格朗日法则是基于粒子的方法，其中界面通过跟踪粒子的运动来描述。

下面将介绍一些常用的界面跟踪方法。

1. 体积法（Volume-of-fluid, VoF）是最常用的界面跟踪方法之一、该方法使用一个控制方程来追踪不同相的体积分数，即在每个格点上定义一个标量变量表示该点处不同相的体积分数。

在模拟过程中，通过对体积分数进行插值和平滑来计算界面的位置。

尽管VoF方法是求解多相流动的广泛应用方法，但在高曲率界面和小尺度现象的处理上存在一些困难。

2. 颜色函数法（Color Function）是另一种常用的界面跟踪方法。

它通过在流场中引入一个描述不同相分布的标量变量，即颜色函数。

当颜色函数等于界面值时，可以确定界面的位置。

颜色函数法对界面的预测较为简单，并且在处理高曲率界面和小尺度现象时具有优势。

3. 其他界面跟踪方法还包括水位线法（Level Set）、界面重构方法（Interface Reconstruction）、粒子追踪方法（Particle Tracking）等。

水位线法是一种常用的界面跟踪方法，它使用一个标量函数来表示各相之间的界面位置，该函数的等值线即为界面。

界面重构方法通过在已知相空间中的数据点上使用适当的插值和平滑方法重建界面。

粒子追踪方法通过跟踪界面上的粒子运动来描绘界面位置。

在实际应用中，界面跟踪方法的选择取决于多相流体系统的特点和需要预测的现象。

不同的界面跟踪方法具有各自的优缺点，需要根据具体情况进行选择和改进。

通过结合不同的界面跟踪方法，可以提高多相流体系统的模拟精度和计算效率。

多相流体力学中的界面跟踪方法在多相流体力学的研究中，界面跟踪是非常重要的一项技术。

界面跟踪的目的是确定各相之间的分界面，以便进行相应的数学模拟。

界面跟踪方法包括光学方法、电磁方法、声波方法、数字图像方法、计算机模拟方法等。

各种方法都有其适用的范围和优缺点，本文将会介绍几种常见的界面跟踪方法。

1. 光学方法光学方法是一种常见的界面跟踪方法，主要是通过光的折射和反射来确定界面的位置。

光学方法可以分为显微镜观察法和激光扫描法两种。

显微镜观察法是一种经典的界面跟踪方法，它通过显微镜观察两相之间的分界面，经过数学转换得到分界面的形状和位置。

这种方法的优点是精度高，但只能应用于局部观测，不适用于整个系统的观测。

激光扫描法是一种新兴的界面跟踪方法，它通过利用激光扫描技术进行测量，可以得到物体表面的形状和位置信息。

这种方法可以应用于整个系统的观测，但其也存在一定的局限性，如对于复杂形状的界面，精度较低。

2. 电磁方法电磁方法是一种界面跟踪方法，在两相界面上加入电磁场，利用电磁场的测量结果来确定界面的位置和形状。

电磁方法包括电阻法、电容法、电感法等。

电阻法是一种比较常用的电磁方法，它通过对两相间的电阻进行监测，从而得到分界面的位置和形状信息。

电容法和电感法则是通过对两相间的电容和电感进行监测，从而得到分界面的位置和形状信息。

这些方法都具有一定的优势，如测量准确、简单易操作等，但是也会受到环境干扰和检测误差的影响。

3. 声波方法声波方法是一种灵敏的界面跟踪方法，它通过测量两相间的声速和波阻抗进行分界面的确定。

其中声速法采用超声波测量，通过不同物质的声速不同，将界面定位出来；波阻抗法则采用声波反射测量，根据反射波的强度和波形可以确定分界面的位置。

声波方法适用于复杂流体介质中的界面跟踪，其具有非接触、无污染等优势。

4. 数字图像方法数字图像方法是一种通过数字图像处理进行界面跟踪的方法，它通过拍摄物体表面的图像，经过计算机图像处理得到分界面的位置和形状。

基于视频的人体运动跟踪与重构方法研究的开题报告标题：基于视频的人体运动跟踪与重构方法研究一、选题背景随着人类社会的不断发展和人类对于智能科技的不断追求，人体运动跟踪和重构技术成为了热门研究领域之一。

对于基于视频的人体运动跟踪和重构方法的研究，可以广泛应用于新型智能设备、虚拟现实、人类姿态分析等领域，提高了人类的生活质量，通过该研究的成果，还可以为人类科学技术的进一步发展提供基础支持。

二、研究目的本研究主要目的是分析人体运动的特点，建立数学模型，设计基于视频的人体运动跟踪与重构方法，并实现模型的验证和应用。

三、研究内容1.人体运动特点的分析和建模；2.基于视频的人体运动跟踪方法的设计；3.人体姿态维度的提取和模式分析；4.基于重建误差和跟踪精度对算法进行优化；5.对模型的验证和应用。

四、研究意义通过本研究，可以为人体运动跟踪和重构技术的进一步发展提供基础支持，并从理论上和实践上提升该技术的应用效能，进一步拓展该技术的应用领域，同时为人类生产生活和科学技术的发展提供有益的支持。

五、研究方法本研究采用基于视频的方法对人体运动进行跟踪和重构，其中包括人体轮廓的提取、图像序列的追踪、运动姿态的重构等步骤。

通过对算法的优化和对模型的验证，最终实现对人体运动的实时跟踪和重构。

六、进度安排1.文献调研和理论准备（2021年10月-2021年11月）；2.人体运动特点的分析和建模（2021年11月-2022年2月）；3.基于视频的人体运动跟踪方法的设计（2022年2月-2022年6月）；4.人体姿态维度的提取和模式分析（2022年6月-2023年1月）；5.基于重建误差和跟踪精度对算法进行优化（2023年1月-2023年6月）；6.对模型的验证和应用（2023年6月-2024年1月）；7.论文的撰写和答辩（2024年1月-2024年6月）。

七、预期成果本研究预期获得以下成果：1.基于视频的人体运动跟踪和重构方法；2.提供一种量化评估人体运动跟踪和重构的指标；3.完成一定的实验和数据采集，形成数据集；4.相关技术的论文和成果发表。

运动界面追踪的CVOFLS方法∗周文;欧阳洁;崔立营【摘要】A new coupled volume of fluid and level set (CVOFLS) method is proposed to capture the moving interface, in order to improve both the inaccurate evaluation of the interface normal vector in volume of fluid (VOF) method and the poor mass conservation ability in level set (LS) method. The method takes the advantages of the VOF method and the LS method. At each time step, the LS equation is solved at first, and the interface normal vector is evaluated via the LS signed distance function. Then the VOF equation is evaluated, and the interface reconstruction and the mass correction are performed by the volume fraction. The method is applied in some benchmark cases, such as rotation of the Zalesak’s disk, and stretching and shrinking of a circular fluid element. The numerical results indicate that the proposed CVOFLS method not only accurately captures the complex interface evolution and preserves the mass conservation, but also greatly improves the computational efficiency.%针对VOF方法中界面法向量计算不准确和level set方法中界面质量守恒性差的缺陷，本文提出了一种新的界面捕捉方法—CVOFLS (coupled volume of fluid and level set)方法．该方法吸收了VOF和level set两种方法的优点，在每个时间步内，首先求解level set输运方程，根据level set符号距离函数计算界面法向量；然后求解VOF输运方程，根据流体体积分数重构界面并校正流体质量．Zalesak 圆盘旋转及圆面剪切的数值模拟表明，该方法能准确捕捉复杂的界面演化过程，具有良好的质量守恒性，并可以提高计算效率．【期刊名称】《工程数学学报》【年(卷),期】2015(000)005【总页数】12页(P697-708)【关键词】运动界面;level set方法;VOF;质量守恒;效率【作者】周文;欧阳洁;崔立营【作者单位】西北工业大学理学院，西安 710129;西北工业大学理学院，西安710129;西北工业大学理学院，西安 710129【正文语种】中文【中图分类】O241 引言生活中许多问题与运动界面息息相关，如石蜡融化、晶体生长、固化和熔化界面以及爆炸、燃烧的气体界面问题[1]，因此，对自由界面数值模拟的研究具有应用价值．目前，自由界面追踪方法依据参照系的不同大致分为Lagrange方法、Euler 方法和Lagrange-Euler混合方法三种．其中，Euler法将描述流体的参照系固定于空间域，是目前最常见的用来描述流体的方法．而在众多Euler方法中，VOF 方法[2]和level set方法[3]因其实施简单、占用内存小且容易处理具有复杂拓扑变化的界面运动问题等优点而被广泛采用．VOF方法是Hirt和Nichols[4]在1981年首先提出的，他成功地对溃坝和涌浪自由面，以及Rayleigh-Taylor不稳定现象进行了数值模拟．虽然该方法有较好质量守恒性，但是很难准确计算界面的法向和曲率．随后，Osher和Sethian[3]于1988年提出了level set方法，该方法通过构造一个等值面函数(level set函数)隐式地追踪界面，可以准确地计算出界面法向与曲率，但是守恒性较差．为了克服传统level set方法质量不守恒的缺点，有学者引入重新初始化技术，借此达到质量校正的目的，但该思想增加了较大的计算量．2005年，Li[5]等提出一种新的变分公式，使得level set函数近似成为符号距离函数．该方法增大了计算时间步长，避免level set方程重新初始化过程，提高了计算效率．但该方法主要应用于图形图像的处理，应用于自由面问题时存在一定难度．针对VOF和level set两种方法存在的问题，一些学者提出了结合两种方法优点的CLSVOF(coupled level set and volume of fluid)方法[6-10]．1995年，Bourlioux[6]提出了CLSVOF方法的基本思想，随后，Sussman和Puckett[7]于2000年给出其详细描述并成功将其应用于三维自由表面的追踪问题，但实施过程较为复杂．针对CLSVOF方法中重构界面的复杂性，Son和Hur[8]于2002年提出了一种完整、有效地重构界面的算法．该算法适用于二维以及轴对称情形的界面重构，随后Son[9]又在2003年将其推广到三维．2006年，Yang等[10]首次基于非结构网格提出一种自适应level set与VOF耦合的方法．虽然该方法理论上精度可达到二阶，但实际效果逊于结构网格上的CLSVOF方法，且程序实现更为复杂．2008年，Pijl等[11]提出了一种基于VOF校正的守恒level set方法，给出了level set函数与VOF函数之间的显示函数关系以达到校正的目的，但校正过程相当复杂且效果不太理想．2010年，Sun和Tao[12]给出了另外一种形式的CLSVOF方法，采用几何原理计算界面附近的level set函数，并省略了level set函数的输运过程．尽管该方法在一定程度上简化了原有的CLSVOF方法，但其几何原理以及界面重构过程比较复杂．2011年，Li等[13]将CLSVOF方法进行改进，提出了一种带质量校正公式的CLSVOF方法．虽然该方法得到了很好的精度，但因其level set函数重新初始化过程的迭代次数太多以致计算效率不高．Wang等[14]于2012年提出了一种新的VOF方法，该方法也是利用VOF与level set方法耦合的思想，它基于VOF 方法中的重构界面构造出精度达到二阶的距离函数，进而提高了计算精度．但是，该方法需要进行两次VOF函数界面重构和level set函数重新初始化，实施过程较为复杂．虽然CLSVOF方法综合了VOF与level set方法的优点，达到高精度的效果．但仍然存在计算量大、程序实施困难、计算不够准确等缺点．而VOF方法同样具有较好守恒性以及高效的优点，但较差的界面法向与曲率成为其缺陷，若将levelset方法计算得到的相对准确界面法向和曲率耦合到VOF方法中，便可克服其缺陷．基于此，本文提出了一种耦合VOF与level set的新方法，记为CVOFLS(coupled volume of fluid and level set)方法．该方法通过level set函数求得相对准确界面法向来校正VOF函数中的界面法向，省去了level set函数重新初始化的过程，因此，可得到更加准确的VOF函数以及更高的计算效率．对经典界面运动问题的模拟，验证了文中所提方法的有效性和准确性．2 输运方程本文采用VOF函数追踪运动界面，并利用level set函数校正VOF函数中的界面法向以保证界面的光滑．下面分别给出在具有速度场u(u,v)的运动介质中，VOF函数F(x,t)与level set函数ϕ(x,t)所满足的输运方程表达式式(1)中VOF函数F(x,t)表示流体在每个体积单元中的体积分数．因此，在含有界面的体积单元中F(x,t)值介于0与1之间，在充满流体的体积单元中F(x,t)值为1，在无流体的体积单元中F(x,t)值为0．而式(2)中level set函数ϕ(x,t)定义为求解区域内的点到流体界面的符号距离函数，设在流体内点的ϕ(x,t)值为正值，在无流体中点的ϕ(x,t)值为负值，在流体界面处点的ϕ(x,t)值为0．在计算level set函数过程中需对ϕ(x,t)重新初始化，使其重新成为点x到界面Γ(t)的符号距离函数，以确保level set函数在整个求解区域上具有非常好的光滑性，并在求解过程中保持较好的数值稳定性．通过求解初值问题的稳态解来实现符号距离函数的重新初始化，其中τ是伪时间．为了使结果变得光顺，重新初始化过程中，sign(ϕ0)采用如下的近似方法∆x,∆y为网格在相应坐标轴方向的空间步长．3 数值方法3.1 VOF输运方程的离散为了计算方便，方程(1)可写为守恒形式本文采用Sussman和Puckett[7]提出的一种通量分裂算法求解方程(4)，其离散形式如下图1给出了流体体积分数F、流体速度(u,v)在结构网格上的分布．数值通量和分别表示沿x方向，y方向考虑单元面流入或流出的流体体积分数．如，表示第n个时间步长∆t内在(i,j)单元中x方向左单元面上所运输的体积分数式中(∆VF)代表输运的流体体积．类似地，可用同样的方法得到第n个时间步长∆t 内x方向右单元面及y方向上、下单元面的流体体积输运量．分别表示第n个时间步长∆t内流体在(i,j)单元中x方向左、右单元面的输运速度，分别表示第n个时间步长∆t内流体在(i,j)单元中y方向上、下单元面的输运速度．图1:VOF控制体示意图为了计算输运的流体体积在每一个时间步长内均需进行界面重构．本文采用Son和Hur[8]提出的VOF-PLIC(piecewise linear interface capturing)格式来重建界面．3.2 Level set输运及重新初始化方程的离散3.2.1 空间离散Level set方程(2)及重新初始化方程(3)均属于Hamilton-Jacobi型方程．其中方程(2)可写为其Hamilton-Jacobi型方程中H(ϕx,ϕy)=uϕx+vϕy，对应的通量为其中对于重新初始化方程(3)，可写为其Hamilton-Jacobi型方程中对应的通量其中故本文空间离散采用Jiang和Peng[15]专门针对Hamilton-Jacobi型方程求解提出的五阶WENO(weighted essentially non-oscillatory)格式．因此，可得level set方程的全离散形式如下其中的推导及表达式详见文献[15]．具体重新初始化方程(3)的全离散形式以及推导过程详见文献[16]．3.2.2 时间项离散为避免求解过程中产生的数值振荡，本文对方程(2),(3)的时间项采用三阶TVD-RK(total variation diminishing Runge-Kutta)格式进行离散．其表达式为其中ϕ(0)= ϕn, ϕ(3)= ϕn+1．对于level set方程(2)，L(ϕ)=uϕx+vϕy对于重新初始化方程(3)，L(ϕ)=sign(ϕ0)(1 − |∇ϕ|)．3.3CVOFLS方法文献[13]中CLSVOF方法的流程如图2(a)所示，其基本思想是根据流体速度按上述方法同时离散level set和VOF方程．该方法以level set方程求解为主体，首先同时初始化level set及VOF函数，在每一时间步长内分别对level set方程、VOF方程进行离散．在VOF函数的界面重构过程中，建立网格单元原点到界面最短距离s与level set函数ϕ之间的关系[16]，随后对level set方程进行重新初始化，并用提出的局部质量校正公式[16]来校正level set函数，以得到更为准确的level set函数．图2:CLSVOF方法和CVOFLS方法流程图虽然CLSVOF方法具有较高的精度，但其在level set函数重新初始化过程中迭代次数过多，从而导致计算效率不高．而本文CVOFLS方法是在CLSVOF方法[13]基础上的改进，它的基本思想是根据流体速度按上述方法同时离散VOF和level set方程，以VOF方程求解为主体，用所求level set函数来校正界面法向(用n 来表示)，在此过程中，省去CLSVOF方法中的level set函数重新初始化过程．由于level set函数得到的界面法向较VOF函数更准确，因此用level set函数得到的界面法向代替求解VOF函数时的界面法向，可以得到更加准确的VOF 函数．其中level set方法得到的界面单位法向n表达式为n=∇ϕ/|∇ϕ|，∇ϕ用中心差分格式进行离散．CVOFLS算法的流程如图2(b)所示，在CVOFLS算法实施过程中，首先同时初始化VOF以及level set函数，在每一时间步长内先求解level set方程以得到界面法向n，再进行VOF方程的求解．离散VOF方程时，用level set函数得到的界面法向n代替VOF函数中的界面法向，随后再进行VOF方法中的重构界面、求解VOF函数等过程，本文最终通过VOF函数来描述自由界面．在整个算法中，由于是以VOF函数的求解为主体，省去了level set重新初始化过程，从而提高了计算效率．4 数值算例为了验证本文提出的CVOFLS方法的有效性，下面分别以平移流场、旋转流场和剪切流场下的运动界面捕捉为例进行数值实验．4.1 平移流场模拟平移流场为一简单常数速度流场，对其数值模拟能够快速有效地验证数值方法的正确性．图3(a)中给定一常数速度场(u,v)=(0.5,−0.2)，图3(b)中给出了平移流场的初始状态．整个计算区域为[0,1]×[0,1]，网格尺寸为0.01×0.01，时间步长为0.0005s．图4中分别给出了粒子level set方法[17]、Young’s VOF方法[17]以及CVOFLS方法在t=1s时的模拟结果．通过对比，CVOFLS方法得到的数值结果比另外两个方法得到的结果略优，从而验证了该方法的正确性．图3:平移流场的初始状态图4:不同方法对平移流场的模拟结果4.2 Zalesak圆盘问题模拟Zalesak圆盘问题常常用来验证自由界面追踪能力．缺口圆盘的半径为0.15，圆心位于(0.50,0.75)处，缺口宽度为0.05．整个流场的计算区域为[0,1]×[0,1]，时间步长为0.0025s．给定的速度场如下该速度场的旋转中心位于(0.50,0.50)处．设初始值为f0，实验值为fi(i=1,2,3,4)，质量盈亏用绝对误差表示，相对误差表示，收敛阶为其中a= ∆x1/∆xi为不同计算网格的空间步长比值．表1给出了本文CVOFLS方法在四种计算网格下模拟Zalesak圆盘问题的绝对误差、相对误差以及收敛阶．数值结果表明CVOFLS方法模拟圆盘问题的准确性，并且该方法也具有较高的收敛阶．图5给出不同计算网格下CVOFLS方法模拟Zalesak圆盘问题的结果．从图中及表1可知，随着网格数量的增加，数值模拟的结果更加准确．表1:CVOFLS方法模拟Zalesak圆盘问题绝对误差、相对误差及收敛阶计算网格i 空间步长∆xi 绝对误差ei 相对误差e′i 收敛阶oi 1 N/A 2 1/50 9.45e-003 0.1425 2.24 3 1/1001.88e-0030.0301 1.79 4 1/1501.22e-0030.0199 1/2001.03e-0030.01701.53图5:CVOFLS方法在不同计算网格下的模拟结果(实线:初始形状，虚线:旋转一周后的形状)图6是Zalesak圆盘问题采用100×100网格进行离散的数值模拟．图中分别给出了level set方法、VOF方法、CLSVOF方法[13]、本文CVOFLS方法在上述速度场下对缺口圆盘旋转一周的模拟结果．从图中可以看出，用CLSVOF与本文CVOFLS方法模拟的结果较好，其所得结果的相对质量误差均小于0.002%，而本文CVOFLS方法的结果略优．但对计算效率而言，表2给出两种方法在不同网格下模拟时间的对比．由表2可见，本文CVOFLS方法在相应网格下的计算效率较CLSVOF方法有显著提高．因此，本文提出的CVOFLS方法具有高精度、高效率以及较好的质量守恒性的优点．图6:CVOFLS方法在不同计算网格下的模拟结果(实线:初始形状，虚线:旋转一周后的形状)表2: 不同计算网格下CLSVOF方法[13]与CVOFLS方法模拟Zalesak圆盘问题的时间计算网格CLSVOF方法(s)CVOFLS方法(s)100×100 65.03 150×150 612.78 156.98 200×200 1336.09 2372.28287.004.3 Zalesak剪切流场模拟平移流场和旋转流场的界面模拟能够验证各种方法的正确性，而剪切流场的界面模拟可以很好地检验界面追踪方法的捕捉能力．下面以二维剪切流场中的界面运动为例，检验CVOFLS方法的模拟效果，即考察圆心在(0.5,0.75)、半径为0.15的圆在速度场中的运动情况，整个流场计算区域为[0,1]×[0,1]，时间步长为0.0025s．其中t为时间，T为返回初始状况所需时间，当t′=T/2时剪切流开始反剪切．图7和图8结果给出T=8s时采用256×256网格对剪切流场界面模拟的结果．其中(a)代表文献[13]中CLSVOF方法模拟结果，(b)代表文献[14]中用NEW VOF方法得到的结果，(c)代表本文CVOFLS方法所模拟的结果．结果显示CVOFLS方法在t=T/2和t=T时刻模拟的结果均优于文献[13,14]，文献[13]中CLSVOF方法模拟结果的相对误差为2.249%，文献[14]中NEW VOF方法模拟结果的相对误差为1.732%，而本文CVOFLS方法模拟的相对误差为1.567%．因此，本文CVOFLS 方法具有很好的界面捕捉能力和质量守恒性．同时，表3给出CLSVOF方法[13]和本文CVOFLS方法在不同网格下模拟剪切流场的时间，验证了CVOFLS方法具有高效的优点．图7: 不同方法模拟二维剪切流场在t=T/2时刻的界面图8: 不同方法模拟二维剪切流场在t=0和t=T时刻的界面表3: 不同计算网格下CLSVOF方法[13]与CVOFLS方法模拟剪切流场的时间计算网格CLSVOF方法(s)CVOFLS方法(s)100×100 127.06 150×150 713.27 284.25 200×200 1507.17 2602.98518.895 结论由于将VOF与level set耦合的方法同时具有两者的优点，故本文基于VOF方法与level set方法耦合的思想，提出了一种新的耦合方法，即CVOFLS方法．数值结果表明：CVOFLS方法对平移流场、Zalesak圆盘以及剪切流场的数值模拟结果验证了方法的准确性，同时表明该方法模拟界面具有较高的追踪精度以及较好的质量守恒性；并且CVOFLS方法易于实施，在求解界面法向时只用到level set函数方程而略去了重新初始化过程，因此大大提高了计算效率．参考文献：[1]刘儒勋，王志峰.运动界面追踪与数值方法[M].合肥：中国科学技术大学出版社，2001 Liu R X,Wang Z F.Movement Interface Tracking and Numerical Method[M].Hefei:University of Science and Technology of ChinaPress,2001[2]Sethian J A.Fast marching methods[J].SIAM Review,1999,41(2):199-235[3]Osher S,Sethian J A.Fronts propagating with curvature dependent speed:algorithms based on Hamilton-Jacobi formulation[J].Journal of Computational Physics,1988,79(1):12-49[4]Hirt C W,Nichols B D.Volume of fluid(VOF)method for the dynamics of free boundary[J].Journal of Computational Physics,1981,39(1):201-225 [5]Li C M,Xu C Y,Gui C F,et al.Level set evolution without re-initialization:a new variational formulation[C]//IEEE CVPR,2005,1(1):430-436[6]Bourlioux A.A coupled level-set volume-of-fluid algorithm for tracking material interfaces[C]//In Proceedings of the 6th International Symposiumon Computational Fluid Dynamics,Canada,1995[7]Sussman M,Puckett E G.A Coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two phase f lows[J].Journal of Computational Physics,2000,162(2):301-337[8]Son G,Hur N.A coupled level set and volume-of-fluid method for Buoyancy-driven motion of fluid particles[J].Numerical Heat Transfer Part B-Fundamentals,2002,42(6):523-542[9]Son G.Efficient implementation of a coupled level-set and volume-of-fluid method for three-dimensional incompressible two-phase f lows[J].Numerical Heat Transfer Part B-Fundamentals,2003,43(6):549-565 [10]Yang X F,James A J,Lowengrub J,et al.An adaptive coupled level-set/volume-of-fluid interface capturing method for unstructured triangular grids[J].Journal of Computational Physics,2006,217(2):364-394[11]van der Pijl S P,Segal A,Vuik C,et puting three-dimensional two-phase f l ows with a massconserving level set method[J].Computing and Visualization in Science,2008,11(4-6):221-235[12]Sun D L,Tao W Q.A coupled volume-of-fluid and levelset(VOSET)method for computing incompressible two-phase f lows[J].International Journal of Heat and Mass Transfer,2010,53(4):645-655 [13]Li Q,Ouyang J,Yang B X,et al.Numerical simulation of gas-assisted injection molding using CLSVOF method[J].Applied Mathematical Modelling,2011,35(1):257-275[14]Wang Z Y,Yang J M,Stern F.A new volume-of-fluid method with a constructed distance function on general structured grids[J].Journal ofComputational Physics,2012,231(9):3703-3722[15]Jiang G S,Peng D.WENO schemes for Hamilton-Jacobiequations[J].Society for Industrial and AppliedMathematics,2000,21(6):2126-2143[16]李强.气辅注射成型及结晶过程数值模拟研究[D].西安：西北工业大学，2011 Li Q.Numerical simulation of gas-assisted injection molding and crystallization process[D].Xi’an:Northwestern Polytechnical University,2011[17]黄莜云.自由界面追踪方法理论研究及数值模拟[D].天津：天津大学，2005 Huang Y Y.Theoretical research and numerical simulation on free surface tracking method[D].Tianjin:Tianjin University,2005。