K2.14 离散系统稳定性判别

线性离散系统的稳定性判据(1) 修正劳斯—胡尔维茨稳定判据连续系统的劳斯—胡尔维茨稳定判据，是通过系统特征方程的系数及其符号来判断系统的稳定性。

这个方法实际上仍是判断特征方程的根是否都在s平面的左半部。

然而，在离散系统中，判断系统的稳定性，是判断系统特征方程的根是否全在z平面的单位圆内。

因此，离散系统不能直接应用劳斯—胡尔维茨判据来分析稳定性。

从理论上分析，利用关系式z=eTs，可以将z为变量的特征方程转换为以s为变量的特征方程。

但因为s在指数中，代换运算不方便。

为此，必须引入另一种线性变换。

将z平面单位圆内区域映射为另一平面上的左半部。

这样，就可以应用劳斯—胡尔维茨稳定判据来判断离散系统的稳定性。

为此，可采用双线性变换方法开展判断。

双线性变换Ⅰ：（1）式中w是复变量，由上式解得（2）或采用双线性变换Ⅱ：（3）或写成（4）此时（5）双线性变换Ⅱ与双线性变换Ⅰ一样，可以将z平面的单位圆变换成w平面的虚轴。

令w平面的虚轴为，则w平面的左半平面为稳定区域，为w平面的频率，且由上式可知其中为s平面的频率。

此时，s平面、z平面以及w平面的关系为图1 s平面、z平面及w平面映射关系当较小时有（6）即w平面的频率近似于s平面的频率。

这是采用双线性变换Ⅱ的优点之一。

另外，双线性变换Ⅱ也与下一章的双线性变换一致，故建议使用双线性变换Ⅱ。

通过z-w变换，就可以应用劳斯—胡尔维茨判据分析线性离散系统的稳定性。

胡尔维茨判据：由系统特征方程各系数组成的主行列式及其顺序主子式全部为正。

该方法随着系统阶数的增加，计算会变得复杂。

此时可以采用下面劳斯判据。

劳斯判据的要点是：①对于特征方程，若系数的符号不一样，则系统不稳定。

若系数符号一样，建立劳斯行列表。

②建立劳斯列表③若劳斯行列表第一列各元素严格为正，则所有特征根均分布在左半平面，系统稳定。

④若劳斯行列表第一列出现负数，系统不稳定。

且第一列元素符号变化的次数，即右半平面上特征根个数。

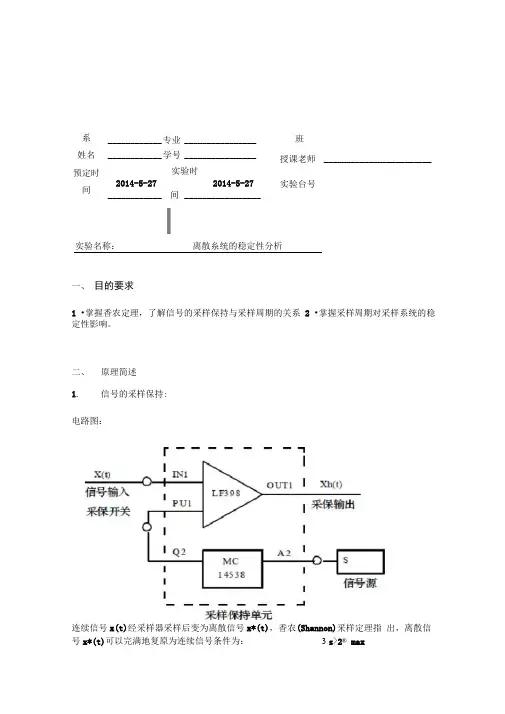
I实验名称：离散糸统的稳定性分析一、 目的要求1 •掌握香农定理，了解信号的采样保持与采样周期的关系2 •掌握采样周期对采样系统的稳定性影响。

二、 原理简述 1.信号的采样保持:电路图：连续信号x(t)经采样器采样后变为离散信号x*(t)，香农(Shannon)采样定理指 出，离散信号x*(t)可以完满地复原为连续信号条件为：3 s >2® max系姓名 预定时 间____________ 专业 ________________ ____________ 学号 ________________ 实验时2014-5-27 2014-5-27____________ 间 _________________班授课老师 ________________________ 实验台号I n I® = -------式中3 S为米样角频率，且',(T为米样周期),3 max为连续信号x (t)的幅频谱| x (j CD 的上限频率T s 若连续信号x (t)是角频率为D S = 22.5的正弦波，它经采样后变为x*(t)，则25（1-尹） ,1 _ 12 占[(2厂一1+訂巧二+ (1—訂「一 27＞力)]0-1)匕-严)闭环脉冲传递函数为：C ⑵12.5[(2厂-l + d + (l -严—22)]丽'一 X 匚(25丁二 13.5 — 11.牝引)二十(12.5 — 11.5邑血—25T 严) 闭环采样系统的特征方程式为：z 2 +(25T-13.5 1 L5e _2r )z+ Q2.5-11 .Se'3r -25Te^T ) = 0特征方程式的根与采样周期T 有关，若特征根的模均小于1,则系统稳定，若有 一个特征根的模大于1,则系统不稳定，因此系统的稳定性与采样周期 T 的大小 有关。

仪器设备PC 机一台，TD-ACC+ (或TD-ACS )教学实验系统一套。

自动控制原理总结之判断系统稳定性方法判断系统稳定性是控制理论研究中的重要内容，正确判断系统的稳定性对于设计和实施控制策略非常关键。

在自动控制原理中，常见的判断系统稳定性的方法主要包括根轨迹法、频率响应法和状态空间法等。

根轨迹法是一种基于系统传递函数的方式来判断系统稳定性的方法。

通过分析系统传递函数的极点和零点的分布，在复平面上绘制出根轨迹图来描述系统特性。

根轨迹图上的点表示系统传递函数的闭环极点位置随控制参数变化的轨迹，通过观察根轨迹图，可以判断系统的稳定性。

一般来说，当根轨迹图上所有的闭环极点都位于左半平面时，系统是稳定的；而如果存在闭环极点位于右半平面，系统就是不稳定的。

此外，根轨迹法还可以通过分析根轨迹图的形状、离散角和角度条件等来进一步评估系统的稳定性。

频率响应法是一种基于系统的频率特性来判断稳定性的方法。

通过分析系统的频率响应曲线，可以得到系统的增益和相位信息，进而判断系统的稳定性。

在频率响应法中，常见的评估指标有增益裕度和相位裕度。

增益裕度表示系统增益与临界增益之间的差距，而相位裕度则表示系统相位与临界相位之间的差距。

一般来说，增益裕度和相位裕度越大，系统的稳定性就越好。

根据增益裕度和相位裕度的要求，可以设计合适的控制器来保证系统的稳定性。

状态空间法是一种基于系统状态方程来判断稳定性的方法。

在状态空间表示中，系统的动态特性由一组一阶微分方程组表示。

通过求解状态方程的特征值，可以得到系统的特征根。

一般来说，当系统的特征根都位于左半平面时，系统是稳定的；而如果存在特征根位于右半平面，系统就是不稳定的。

此外，状态空间法可以通过观察系统的可控和可观测性来进一步判断系统稳定性。

当系统可控和可观测时，系统往往是稳定的。

除了以上几种常见的判断系统稳定性的方法外，还有一些其他的方法，如Nyquist稳定性判据、Bode稳定性判据、李雅普诺夫稳定性判据等。

这些方法各有特点，常常根据具体的系统和问题选择合适的方法来判断稳定性。

实验一 离散系统稳定性分析实验学时：2 实验类型：常规 实验要求：必作一、实验目的：（1）掌握利用MATLAB 绘制系统零极点图的方法； （2）掌握离散时间系统的零极点分析方法；（3）掌握用MATALB 实现离散系统频率特性分析的方法； （4）掌握逆Z 变换概念及MATLAB 实现方法； （5）掌握用MATLAB 分析离散系统稳定性。

二、实验原理：1、离散系统零极点图及零极点分析；线性时不变离散系统可用线性常系数差分方程描述，即()()NMiji j a y n i b x n j ==-=-∑∑ （8-1）其中()y k 为系统的输出序列，()x k 为输入序列。

将式（8-1）两边进行Z 变换的00()()()()()Mjjj Nii i b zY z B z H z X z A z a z-=-====∑∑ （8-2） 将式（8-2）因式分解后有：11()()()Mjj Nii z q H z Cz p ==-=-∏∏ （8-3）其中C 为常数，(1,2,,)j q j M =为()H z 的M 个零点，(1,2,,)i p i N =为()H z 的N个极点。

系统函数()H z 的零极点分布完全决定了系统的特性，若某系统函数的零极点已知，则系统函数便可确定下来。

因此，系统函数的零极点分布对离散系统特性的分析具有非常重要意义。

通过对系统函数零极点的分析，可以分析离散系统以下几个方面的特性：● 系统单位样值响应()h n 的时域特性； ● 离散系统的稳定性；离散系统的频率特性； 1.1、零极点图的绘制设离散系统的系统函数为则系统的零极点可用MA TLAB 的多项式求根函数roots()来实现，调用格式为：p=roots(A)其中A 为待根求多项式的系数构成的行矩阵，返回向量p 则是包含多项式所有根的列向量。

如多项式为231()48B z z z =++，则求该多项式根的MA TLAB 命令为为： A=[1 3/4 1/8];P=roots(A) 运行结果为： P =-0.5000 -0.2500需注意的是，在求系统函数零极点时，系统函数可能有两种形式：一种是分子、分母多项式均按z 的降幂次序排列；另一种是分子、分母多项式均按1z -的升幂次序排列。

信号与系统稳定性的判断方法信号与系统的稳定性是指系统的输出在有限时间内是否始终有界。

在信号与系统学科中，稳定性是十分重要的一个概念，它关乎到系统的可控性、可观测性、性能优化等方面。

在工程实践中，对于不稳定的系统，我们需要通过判断及时作出调整和改进。

本文将详细介绍信号与系统稳定性的判断方法。

首先，我们来讨论连续时间系统的稳定性判断方法。

对于线性时不变系统，它的稳定性可以通过系统的传递函数来判断。

连续时间系统的传递函数一般可以表示为H(s)，其中s是复频域变量。

连续时间系统稳定的条件是传递函数H(s)的所有极点都位于s平面的左半实轴（实部小于零）上。

对于离散时间系统，其稳定性判据是类似的。

离散时间系统的传递函数一般可以表示为H(z)，其中z是复平面变量。

离散时间系统稳定的条件是传递函数H(z)的所有极点都位于单位圆内（绝对值小于1）。

除了传递函数法外，还有一些其他方法可以判断系统的稳定性。

以下是几种常见的方法：1.查看系统的单位冲激响应：通过单位冲激响应来观察系统的输出是否有界。

如果单位冲激响应在有限时间内衰减到零，则系统是稳定的。

2.查看系统的单位步响应：步响应是指系统对一个单位阶跃输入的响应。

通过观察单位步响应是否趋于稳定，可以初步判断系统是否稳定。

3.利用系统的状态方程：如果系统的状态方程满足严格李雅普诺夫稳定条件（所有特征根的实部小于零），则系统是稳定的。

该方法适用于线性时不变系统。

4.利用系统的瞬态响应：观察系统的瞬态响应是否为有界信号。

如果系统的瞬态响应在有限时间内衰减到零，则系统是稳定的。

5.利用系统的BIBO稳定性：系统的BIBO稳定性（有界输入有界输出稳定性）可以通过观察系统的单位采样响应是否有界来判断。

如果系统的单位采样响应是有界的，则系统是稳定的。

需要注意的是，以上方法并非普遍适用于所有类型的系统。

对于一些非线性系统、时变系统，以上方法可能不适用或者判断结果不准确。

在实际应用中，还可以结合仿真实验、数值计算等方法来进行稳定性判断。