一次函数k和b的意义

第5周一次函数——平移与k 、b 性质一、平移方法：直线y=kx+b 与y 轴交点为（0，b ），直线平移则直线上的点（0，b ）也会同样的平移，平移不改变斜率k ，则将平移后的点代入解析式求出b 即可。

直线y=kx+b 向左平移2，向上平移3 <=>y=k(x+2)+b+3;（“左加右减，上加下减”）。

1.直线y=5x-3向左平移2个单位得到直线 2.直线y=-x-2向右平移2个单位得到直线 3.直线y=21x 向右平移2个单位得到直线 4.直线y=223+-x 向左平移2个单位得到直线 5.直线y=2x+1向上平移4个单位得到直线 6.直线y=-3x+5向下平移6个单位得到直线 7.直线x y 31=向上平移1个单位，再向右平移1个单位得到直线。

8.直线143+-=x y 向下平移2个单位，再向左平移1个单位得到直线________。

9.过点（2，-3）且平行于直线y=2x 的直线是 10.过点（2，-3）且平行于直线y=-3x+1的直线是___________.11．把函数y=3x+1的图像向右平移2个单位再向上平移3个单位，可得到的图像表示的函数是____________；12．直线m:y=2x+2是直线n 向右平移2个单位再向下平移5个单位得到的，而（2a,7）在直线n 上，则a=____________； 二、函数图像及其性质☆一次函数y=kx+b （k≠0）中k 、b 的意义：k(称为斜率)表示直线y=kx+b （k≠0）的倾斜程度； b （称为截距）表示直线y=kx+b （k≠0）与y 轴交点的，也表示直线在y 轴上的。

☆同一平面内，不重合的两直线y=k 1x+b 1（k 1≠0）与y=k 2x+b 2（k 2≠0）的位置关系： 当时，两直线平行。

当时，两直线垂直。

当时，两直线相交。

当时，两直线交于y 轴上同一点。

☆特殊直线方程： X 轴:直线Y 轴:直线与X 轴平行的直线与Y 轴平行的直线 一、三象限角平分线二、四象限角平分线1、对于函数y ＝5x+6，y 的值随x 值的减小而___________。

一次函数的图象和性质【知识要点】1.一次函数的概念：函数y=kx ＋b （k ，b 为常数，k ≠0）叫做x 的一次函数。

学习这个定义应明确下面几点：函数y=kx ＋b （k ≠0）中b 可以为任意常数，当b=0时，一次函数y=kx ＋b 就成y=kx （k 为常数，且（k ≠0）），这时y 叫做x 的正比例函数，也可以说y 与x 成正比例，常数k 叫做因变量y 与自变量x 的比例系数．因此正比例函数是一次函数的特例，但一次函数不一定是正比例函数。

2.一次函数的图像：一次函数y ＝kx ＋b （k ≠0）的图像是一条与坐标轴斜交的直线。

因此，只需求出直线y ＝kx ＋b 上的两点，就可得到它。

一般，作正比例函数y ＝kx 的图像常取点（0，0）和（1，k ）；作一次函数)0(≠+=b b kx y 的图像常取（b ,0）和（0,k b-）两点，这两点是直线与坐标轴的交点。

3.一次函数的性质：（1）参数k 、b 的意义和对一次函数y ＝kx ＋b 的图像与性质的影响。

当k>0时，图像一定过一、三象限，y 随x 的增大而增大，这时函数的图像从左到右呈上升趋势；当k<0时，图像一定过二、四象限，y 随x 的增大而减小，这时函数的图像从左到右呈下降趋势；（因此，k 的符号与直线的方向、函数的增减性是相互决定的。

）（2）b 是一次函数y ＝kx ＋b 中，当x ＝0时所对应的函数值，因此直线y ＝kx ＋b 与y 轴交于点（0，b ），b 是直线y ＝kx ＋b 与y 轴上的交点的纵坐标，所以，b 的符号和直线与y 轴交点位置是相互对应的。

（3）k 、b 的符号对直线位置的影响：【小试牛刀】 1、一个正比例函数y kx=的图象经过点A （-2，4），写出这个正比例函数的表达式 ．2、一辆汽车和一辆摩托车分别从A ,B 两地去同一城市,它们离A 地的路程随时间变化的图象如图所示.则下列结论错误．．的是（ ） A.摩托车比汽车晚到1 h B. A , B 。

一次函数的定义一、引入共同特征：函数的关系式都是用含自变量的一次整式 二、归纳1、一次函数的定义：函数的关系式都是用含自变量的一次整式表示的函数。

式子表示：y ＝kx ＋b (k,b 为常数，k ≠0)条件：○1含自变量 ○2自变量的次数为1 ○3整式 特别地，当b=0,一次函数y=kx(k ≠0)叫正比例函数 注：（1）对于y ＝kx ＋b当k ≠0,b 为任意数时是一次函数 当k ≠0,且b=0时是正比例函数 (2)正比例函数是特殊的一次函数 一次函数不一定是正比例函数(3)若y 是x 的一次函数关系，则函数关系一定可表示为y ＝kx ＋b (k ≠0)形式,反过来，能化为y ＝kx ＋b (k ≠0)形式的函数一定是一次函数若y 是x 的正比例函数关系，则函数关系一定可表示为y ＝kx (k ≠0)形式,反过来，能化为y ＝kx (k ≠0)形式的函数一定是正比例函数 三、典例1、函数：○1y=2x ○2y=4x=3 ○3y=12○4y=3x +1 ○5y=3x+1 ○6y=ax ○7xy=3 ○82x+3y-1=0 ○9y=12x 2+1 ○10y=x2 ○11 y=x(x-4)-x 2 ○12 y=-5x 2_ 一次函数是__________ ___ 正比例函数是___________2、 关于x 的函数y=(5m-3)x 2-m+(m+n) (1) 当m 、n 为何值时，它是一次函数 (2) 当m 、n 为何值时，它是正比例函数。

3、 关于x 的函数3)3(3+--=-n xm y m(1) 当m 、n 为何值时，它是一次函数(2) 当m 、n 为何值时，它是正比例函数。

4、 已知y 与x-3成正比例，当x=4时，y=3(1) 写出y 与x 的函数关系式 (2) Y 与x 之间是什么函数关系。

(3) 当x=2.5时，求y 的值。

小结：1. y 与x 成正比例，则函数关系可设为y=kx(k ≠0)2. 成正比例不一定是正比例函数，但正比例函数一定成正比例。

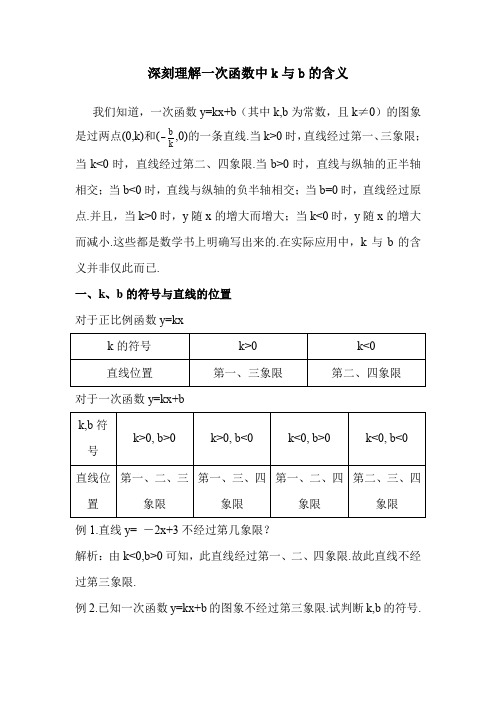
深刻理解一次函数中k 与b 的含义我们知道，一次函数y=kx+b （其中k,b 为常数，且k ≠0）的图象是过两点(0,k)和(kb ,0)的一条直线.当k>0时，直线经过第一、三象限；当k<0时，直线经过第二、四象限.当b>0时，直线与纵轴的正半轴相交；当b<0时，直线与纵轴的负半轴相交；当b=0时，直线经过原点.并且，当k>0时，y 随x 的增大而增大；当k<0时，y 随x 的增大而减小.这些都是数学书上明确写出来的.在实际应用中，k 与b 的含义并非仅此而已.一、k 、b 的符号与直线的位置 对于正比例函数y=kxk 的符号 k>0 k<0 直线位置 第一、三象限第二、四象限对于一次函数y=kx+b k,b 符号k>0, b>0k>0, b<0k<0, b>0k<0, b<0直线位置第一、二、三象限第一、三、四象限第一、二、四象限第二、三、四象限例1.直线y= －2x+3不经过第几象限？解析：由k<0,b>0可知，此直线经过第一、二、四象限.故此直线不经过第三象限.例2.已知一次函数y=kx+b 的图象不经过第三象限.试判断k,b 的符号.解析：根据题意可知，直线y=kx+b 在平面直角坐标系中的位置可以分为以下两种情况：⑴如图1，直线y=kx+b 经过第一、二、四象限，此时，k<0,b>0； ⑵如图2，直线y=kx+b 经过第二、四象限，此时，k<0,b=0. 综上所述，可知，k,b 的符号为：k<0,b ≥0.二、k 的大小与函数值的增减速度一次函数y=kx+b 中，k 越大，直线越陡峭，函数值增减速度越快；k 越小，直线越平缓，函数值增减速度越慢；k=0时，直线与横轴平行，函数值保持不变，此时，函数值没有增减变化. 例3.如图，请举出一个实际情境来进行描述它.解析：结合本题图象，可以考虑利用距离、时间、速度来对此进行描述.解：王爷爷早晨外出散步.他从家里出发以慢速匀速行走，到了报亭前，他看了一会儿报纸，然后以快速匀速回到家里.则王爷爷离家的距离s(m)与行走时间t(min)的函数关系 可以用来描述此图象.三、k 的值与实际应用问题在利用一次函数解决实际问题中，如果函数值逐渐增大，那么k>0；如果函数值逐渐减少，那么k<0；如果函数值保持不变，那么例3图t / mins / m ox y o xy o 图⑴ 图⑵例2图k=0；如果两个一次函数y 1=k 1x+b 1与y 2=k 2x+b 2的增减速度相同，那么21k k =.例4.一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为(h)x ，两车之间的距离．．．．．．．为(km)y ，图中的折线表示y 与x 之间的函数关系． 根据图象进行以下探究： 信息读取（1）甲、乙两地之间的距离为 km ； （2）请解释图中点B 的实际意义； 图象理解（3）求慢车和快车的速度；（4）求线段BC 所表示的y 与x 之间的函数关系式，并写出自变量x 的取值范围； 问题解决（5）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？ 解：（1）900；（2）图中点B 的实际意义是：当慢车行驶4h 时，慢车和快车相遇． （3）由图象可知，慢车12h 行驶的路程为900km ， 所以慢车的速度为90075(km /h)12=； 当慢车行驶4h 时，慢车和快车相遇，两车行驶的路程之和为900km ，（第28题）ABC DOy /km 90012 x /h4所以慢车和快车行驶的速度之和为900225(km /h)4=，所以快车的速度为150km/h ．（4）根据题意，快车行驶900km 到达乙地，所以快车行驶9006(h)150=到达乙地，此时两车之间的距离为675450(km)⨯=，所以点C 的坐标为(6450)，．设线段BC 所表示的y 与x 之间的函数关系式为y kx b =+，把(40)，，(6450)，代入得044506.k b k b =+⎧⎨=+⎩，解得225900.k b =⎧⎨=-⎩， 所以，线段BC 所表示的y 与x 之间的函数关系式为225900y x =-． 自变量x 的取值范围是46x ≤≤．（5）慢车与第一列快车相遇30分钟后与第二列快车相遇，此时，慢车的行驶时间是4.5h ．把 4.5x =代入225900y x =-，得112.5y =．此时，慢车与第一列快车之间的距离等于两列快车之间的距离是112.5km ，所以两列快车出发的间隔时间是112.51500.75(h)÷=，即第二列快车比第一列快车晚出发0.75h ．。

一次函数中k和b的意义
对于一次函数y=kx+b(k、b为常数，k≠0），“k”决定图象的变化趋势（增减性），也就是斜率，而“b”决定图象与y轴的交点坐标（位置），就是截距。

一次函数中的k表示斜率，b指的是截距。

斜率，数学、几何学名词，是表示一条直
线（或曲线的切线）关于（横）坐标轴倾斜程度的量。

它通常用直线（或曲线的切线）与（横）坐标轴夹角的正切，或两点的纵坐标之差与横坐标之差的比来表示。

一次函数是函
数中的一种，一般形如y=kx+b（k，b是常数，k≠0），其中x是自变量，y是因变量。

特别地，当b=0时，y=kx（k为常数，k≠0），y叫做x的正比例函数（directproportionfunction）。

当k\ue0时，直线y=kx+b(k≠0）的图象从左到右就是下降的；
当k\uc0时，直线y=kx+b(k≠0)的图象从左到右是下降的。

k就可以同意函数的方向也就是函数从左往右看看究竟就是减小还是增大的 b同
意的就是函数与y轴的交点。

一次函数考点知识梳理1.一次函数定义：o一次函数的一般形式为y=kx+b（k≠0），其中k是斜率，b 是y轴截距。

o理解并掌握一次函数的图像特征：直线、方向（上升或下降）、位置（与坐标轴的交点）。

2.斜率的理解和应用：o斜率的意义：表示直线的倾斜程度，斜率为正时，直线从左向右上升；斜率为负时，直线从左向右下降。

o计算斜率的方法：两点式斜率公式k=(y2-y1)/(x2-x1)。

o判断两条直线平行或垂直的关系：若两直线斜率相等，则两线平行；若一直线斜率为另一直线斜率的相反数且绝对值相等，则两线垂直。

3.一次函数图像平移变换：o水平平移：原函数y=kx+b平移h个单位后变为y=k(x-h)+ b，其中h>0向右平移，h<0向左平移。

o垂直平移：原函数y=kx+b向上平移k个单位后变为y=kx+b +k，向下平移则减去相应的单位。

4.一次函数的实际应用问题：o表示实际生活中的增长、减少、路程与时间关系等问题，理解“速度”即斜率的概念。

o解决与一次函数相关的面积计算、行程问题、利润问题等。

5.一次函数与方程、不等式的联系：o一次函数解析式可以转化为一元一次方程和一元一次不等式，通过求解方程或不等式来确定图像上的点或区域。

6.一次函数与坐标轴的交点坐标：o求解一次函数与x轴和y轴的交点坐标，从而确定函数图形的具体位置。

7.线性关系与一次函数模型：o在实际问题中建立一次函数模型，通过观察数据、分析趋势确定变量之间的线性关系，并用一次函数的形式表示出来。

o学会从表格、图象或具体情境中提取信息，构建并验证一次函数模型。

8.一次函数图像特征与性质：o根据k和b的符号及绝对值大小，判断一次函数图像经过的象限（一、二、三、四象限）以及单调性（增函数还是减函数）。

o了解两点决定一条直线的原理，并能利用两个点坐标画出一次函数图像。

9.一次函数与反比例函数、二次函数的区别与联系：o明确一次函数是一次项系数不为零的多项式函数，而反比例函数是y=k/x形式，二次函数是y=ax²+bx+c形式，理解它们在图形、性质上的差异与共同点。

精心整理第5周 一次函数——平移与k 、b 性质一、平移方法：直线y=kx+b 与y 轴交点为（0，b ），直线平移则直线上的点（0，b ）也会同线4. 直线y=223+-x 向左平移2个单位得到直线5. 直线y=2x+1向上平移4个单位得到直线6. 直线y=-3x+5向下平移6个单位得到直线7. 直线x y 31=向上平移1个单位，再向右平移1个单位得到直线 。

8. 直线13+-=x y 向下平移2个单位， ☆一次函数y=kx+b （k≠0）中k 、b 的意义：k(称为斜率)表示直线y=kx+b （k≠0） 的倾斜程度；精心整理 b （称为截距）表示直线y=kx+b （k≠0）与y 轴交点的 ，也表示直线在y 轴上的 。

☆同一平面内，不重合的两直线 y=k 1x+b 1（k 1≠0）与 y=k 2x+b 2（k 2≠0）的位置关系：X 轴与X 12、对于函数1223y x =-,y 的值随x 值的________而增大。

3、一次函数 y=(6-3m)x ＋(2n －4)不经过第三象限，则m 、n 的范围是__________。

4、直线y=(6-3m)x ＋(2n －4)不经过第三象限。

象限。

三、综合1、已知23y -与31x +成正比例，且2x =时，5y =（1）求y 与x 之间的函数关系式，并自行建立直角坐标系画出该函数图像； （2）当a 为多少时，点(),2a 在这个函数的图象上 .2、已知x+a 与y+b 成正比例，且x=1时y ＝－1 ； x=2时y=2。

(1)求y与x的函数关系式 (2)作出函数的图象(3)利用图象回答当x为何值时，y等于零，y大于零，y小于零？3、某校部分住校生，放学后到学校锅炉房打水，每人接水2升，他们先同时打开两个放水龙头，后来因故障关闭一个放水龙头．假设前后两人接水间隔时间忽略不计，且不(1)(2)45、直线式。

☆☆1（3，4求直线的解析式。

3、一次函数的图像与y=2x-5平行且与4、若一次函数y=kx+b的自变量x的取值范围是-2≤x≤6，x轴交于点（-2,0）求解析式。