双自由度系统

第四章两自由度系统的振动介绍第四章是关于两自由度系统的振动的介绍。

在这一章中，我们将探讨两自由度系统的振动模型、动力学方程，并讨论其解析解和数值解。

此外，我们还将介绍两自由度系统的模态分析、共振现象以及一些相关的应用。

两自由度系统是一种具有两个自由度的振动系统，它由两个具有质量和弹性的物体通过柔性连接件或刚性连接件相互连接而成。

这些物体可以是质点、弹性体或刚体等，而连接件可以是弹性杆、弹簧、细梁等。

在两自由度系统中，每个物体都可以做平动或转动运动，因此系统具有两个自由度。

例如，双摆锤、双弹簧振子等都属于两自由度系统。

两自由度系统的动力学方程可以由拉格朗日方程或牛顿第二定律得到。

得到动力学方程后，我们可以通过解方程得到系统的解析解，以获得系统的振动特性。

在分析解时，通常要求系统的运动是简谐振动或近似简谐振动。

另一种求解两自由度系统的方法是数值解法。

数值解法可以通过数值积分来近似求解动力学方程，这种方法常用于求解复杂的系统，或者对系统参数进行优化等情况。

分析解和数值解法可以用来研究两自由度系统的固有振动频率、振型和动态响应等。

通过模态分析，我们可以得到系统的固有频率，并确定每个模态的振型。

对于实际工程问题，模态分析可以帮助我们了解系统的共振情况，并设计出合适的控制策略，以求减小共振现象的发生。

共振是两自由度系统中一个重要而常见的振动现象。

当外力的频率与系统的固有频率接近时，系统会发生共振现象。

共振的发生会导致系统振幅的急剧增加，并且可能对系统的稳定性产生不利影响。

因此，在设计过程中，需要避免共振现象的发生，并采取合适的措施来控制共振。

此外，两自由度系统的振动也有许多实际应用。

例如，双摆锤可以用来研究天体运动和天文学现象；双弹簧振子可以用来研究建筑物或桥梁的振动特性；双振子可以用来研究分子振动和分子动力学等。

总而言之，两自由度系统的振动是一种普遍且重要的物理现象。

通过对两自由度系统进行建模和分析，我们可以深入了解系统的振动特性，并在实际应用中进行优化和改进。

两个自由度系统频率和模态测量实验一、实验目的1、研究具有两集中质量的悬臂梁的动力系统特性，并将基本概念、方法及所得结论推广到多自由度系统；2、掌握结构（系统）的固有频率和振型的基本概念及其物理意义，加深对两自由度结构（多自由度系统）自由振动的规律及特性的认识；3、掌握模态实验的基本步骤和方法，加深对结构动力学基本理论的理解；4、了解动态测试仪器的基本工作原理，熟悉模态分析软件的基本操作过程及使用方法。

二、实验内容1、测试具有两个集中质量的悬臂梁的固有频率和振型；2、根据实验数据计算质量归一化振型； 三、实验原理1、参数识别基本理论本实验采用锤击法测定具有两个集中质量的悬臂梁的固有频率和振型，采用分量分析法进行上述参数的识别。

首先测试系统的频响函数，依据结构动力学理论，运算得出、r s 两点间的频响函数可写成下式：rs H ()()()21(12)nr ri sirs i s i i i i X H F k i ωϕϕωωλζλ===−+∑(1)由于实验测试为加速度响应，设圆频率为ω，位移函数,sin t X x ω=因此加速度函数为2sin a X t 2x ωωω=−=−，用复数表示后，参照(1-1)式可得到加速度频响函数为2221(12)nari si r rs i s i i i iX H F k i ϕϕωωλζλ=−==−−+∑ (2) 由公式(1-2)可知，当k ωω=时，1k λ=，此时式(1-2)可近似写为：2()22ark sk rk sk rs k k k k k kH i k i m ,ϕϕϕϕωωωζζ==−=− (3) 它对应频响函数ars H 的幅频曲线的第k 个峰值，其中在上面(1-3)2kk kk m ω=式中为第阶模态质量。

改变k s 点的位置，在不同点激振，可以得到不同点与点之间的频响函数，当r s r =时，可得到点r 处的原点频响函数为：221(12)nari ri rr i i i H k i ϕϕωi λζλ==−−+∑ (4) 它的第个峰值为：k 2()2ark rk rr k k k kH i k ,ϕϕωωωζ==− (5)由(1-3)/ (1-5)得到()()a rs k skarr k rkH H ωωϕωωϕ=== (6) 若另，就可得到：1rk ϕ=(()ars k sk arr k H H )ωωϕωω=== (7) 由(1-7)式，令1,2,,s n ="，就可得到第阶主振型的各个元素。

第五章两自由度系统振动§5-1 概述单自由度系统的振动理论是振动理论的基础。

在实际工程问题中，还经常会遇到一些不能简化为单自由度系统的振动问题，因此有必要进一步研究多自由度系统的振动理论。

两自由度系统是最简单的多自由度系统。

从单自由度系统到两自由度系统，振动的性质和研究的方法有质的不同。

研究两自由度系统是分析和掌握多自由度系统振动特性的基础。

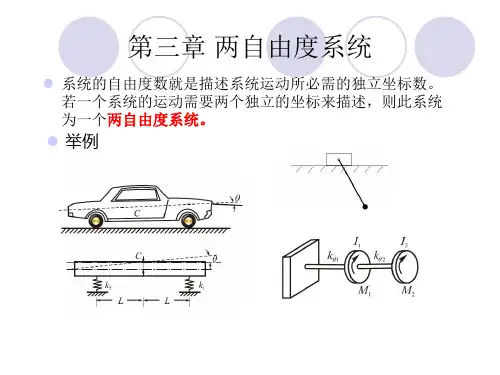
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。

很多生产实际中的问题都可以简化为两自由度的振动系统。

①汽车动力学模型：图3.1两自由度汽车动力学模型§5-2 两自由度系统的自由振动一、系统的运动微分方程②以图3.2的双弹簧质量系统为例。

设弹簧的刚度分别为k 1和k 2，质量为m 1、m 2。

质量的位移分别用x 1和x 2来表示，并以静平衡位置为坐标原点，以向下为正方向。

(分析)在振动过程中的任一瞬间t ，m 1和m 2的位移分别为x 1及x 2。

此时，在质量m 1上作用有弹性恢复力()12211x x k x k -及，在质量m 2上作用有弹性恢复力()122x x k -。

这些力的作用方向如图所示。

应用牛顿运动定律，可建立该系统的振动微分方程式：()()⎭⎬⎫=-+=--+00122221221111x x k x m x x k x k xm （3.1）令2212121,,m k c m k b m k k a ==+=则（3.1）式可改写成如下形式：()()⎭⎬⎫=-+=--+00122221221111x x k x m x x k x k xm⎭⎬⎫=+-=-+00212211cx cx xbx ax x（3.2） 这是一个二阶常系数线性齐次联立微分方程组。

(分析)在第一个方程中包含2bx -项，第二个方程中则包含1cx -项，称为“耦合项”（coupling term ）。

这表明，质量m 1除受到弹簧k 1的恢复力的作用外，还受到弹簧 k 2的恢复力的作用。

第四章两自由度系统的振动当振动系统需要两个独立坐标描述其运动时，称为两自由度振动系统。

两自由度系统是最简单的多自由度系统，因此研究两自由度系统是分析和掌握多自由度系统的基础。

两自由度系统具有两个固有频率，两自由度系统以固有频率进行的振动与单自由度系统不同，它以固有频率进行的振动是指整个系统在运动过程中莫一位移形状，称为固有振型，因此两自由度具有两个与固有频率对应的两个固有振型。

在任意初始条件下的自由振动响应一般由两个固有振型的叠加得到。

受迫简谐振动的频率与激励频率相同。

两自由度系统的振动微分方程一般由两个联立的微分方程组成。

如果恰当地选取坐标，可使两个微分方程解除耦合，这种坐标称为主坐标或固有坐标。

用固有坐标建立的系统振动微分方程为两个独立的单自由度系统的微分方程。

4．1系统的自由振动如图所示的无阻尼两质量-弹簧系统，可沿光滑水平面滑动的两个质量与分别用弹簧与连至定点，并用弹簧相互连接。

三个弹簧的轴线沿同一水平线，质量与只限于沿着该直线进行往复运动。

这样与的任一瞬时的位置只需用坐标与就可以完全确定，因此该系统具有两个自由度。

图两自由度系统的振动取与的静平衡位置为坐标原点。

在振动过程中任一瞬时t,与的位置分别为与，作用于与的重力于光滑水平面的法向反力相平衡，在质量的水平方向作用有弹性恢复力和，质量的水平方向则受到和作用，方向如图所示。

取加速度和力的正方向与坐标正方向一致，根据牛顿运动定律有移项得方程（）就是图所示的两自由度系统自由振动的微分方程，为二阶常系数线性齐次常微分方程组。

方程（）可以使用矩阵形式来表示，写成由系数矩阵组成的常数矩阵m和k分别称为质量矩阵和刚度矩阵，向量x 称为位移向量。

因此设分别为刚度矩阵k中的元素，因而方程（）可以写成方程（）为系统自由振动的微分方程。

方程（）是齐次的，如果和位方程（）的一个解，那么与其相差一个因子的和也将是一个解。

通常感兴趣的是一种特殊形式的解，也就是和同步运动的解。

二自由度系统响应曲线matlab二自由度系统响应曲线matlab一、引言二自由度系统是指具有两个自由度的系统，其动力学行为可以用两个一阶微分方程描述。

在工程领域中，二自由度系统广泛应用于建筑结构、机械振动、航空航天等领域。

了解二自由度系统的响应曲线对于设计和优化这些系统至关重要。

二、理论基础1. 二自由度系统模型在建筑结构中，常见的二自由度模型是质量-弹簧-阻尼器模型。

该模型包含两个质点和两个弹簧阻尼器组成，如图所示。

其中，m1和m2分别为两个质点的质量；k1和k2分别为两个弹簧的刚度；c1和c2分别为两个阻尼器的阻尼系数；x1(t)和x2(t)分别为两个质点的位移。

2. 二自由度系统方程根据牛顿第二定律，可以得到二自由度系统的运动方程：m1x''1 + c1x'1 + k1(x1 - x2) + k2x1 = F(t)m2x''2 + c2x'2 + k1(x2 - x1) = 0其中，x''1和x''2分别为两个质点的加速度；x'1和x'2分别为两个质点的速度；F(t)为外部激励力。

3. 二自由度系统特征频率假设二自由度系统没有阻尼，则其特征频率可以表示为：ω1 = sqrt(k1/m1)ω2 = sqrt((k1 + k2)/m2)其中，ω1和ω2分别为两个质点的固有频率。

4. 二自由度系统阻尼比阻尼比是描述阻尼器对系统运动的影响程度的参数。

假设二自由度系统存在阻尼，则其阻尼比可以表示为：ζ1 = c1/(2sqrt(k1m1))ζ2 = c2/(2sqrt((k1 + k2)m2))其中，ζ1和ζ2分别为两个质点的阻尼比。

三、matlab模拟在matlab中，可以通过ode45函数求解二自由度系统方程。

具体步骤如下：Step 1：定义方程在matlab中，可以通过function关键字定义一个函数来表示方程。