0727第三章 两自由度系统振动(讲)共20页文档
- 格式:doc
- 大小:506.00 KB
- 文档页数:19



第三章两自由度系统振动§3-1 概述单自由度系统的振动理论是振动理论的基础。
在实际工程问题中,还经常会遇到一些不能简化为单自由度系统的振动问题,因此有必要进一步研究多自由度系统的振动理论。
两自由度系统是最简单的多自由度系统。
从单自由度系统到两自由度系统,振动的性质和研究的方法有质的不同。
研究两自由度系统是分析和掌握多自由度系统振动特性的基础。
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。
很多生产实际中的问题都可以简化为两自由度的振动系统。
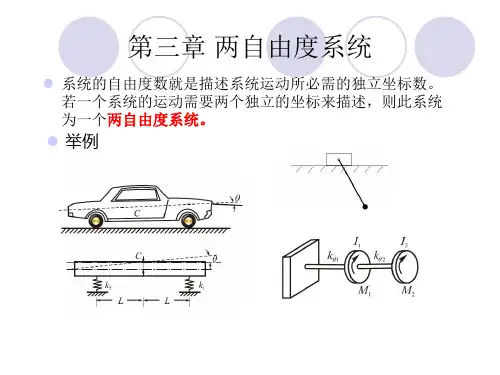
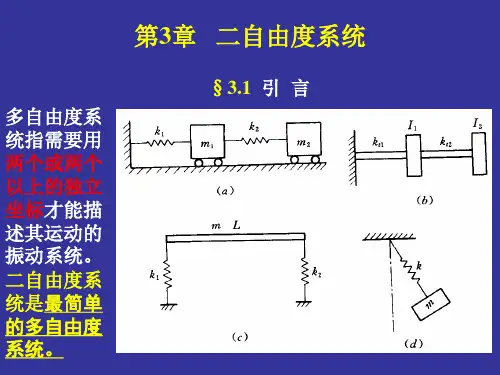
例如,车床刀架系统(a)、车床两顶尖间的工件系统(b)、磨床主轴及砂轮架系统(c)。
只要将这些系统中的主要结合面(或芯轴)视为弹簧(即只计弹性,忽略质量),将系统中的小刀架、工件、砂轮及砂轮架等视为集中质量,再忽略存在于系统中的阻尼,就可以把这些系统近似简化成图(d)所示的两自由度振动系统的动力学模型。
以图3.1(c)所示的磨床磨头系统为例分析,因为砂轮主轴安装在砂轮架内轴承上,可以近似地认为是刚性很好的,具有集中质量的砂轮主轴系统支承在弹性很好的轴承上,因此可以把它看成是支承在砂轮架内的一个弹簧——质量系统。
此外,砂轮架安装在砂轮进刀拖板上,如果把进刀拖板看成是静止不动的,而把砂轮架与进刀拖板的结合面看成是弹簧,把砂轮架看成是集中的质量,则砂轮架系统又近似地可以看成是支承在进刀拖板上的另一个弹簧——质量系统。
这样,磨头系统就可以近似地简化为图示的支承在进刀拖板上的两自由度系统。
在这一系统的动力学模型中,m1是砂轮架的质量,k1是砂轮架支承在进刀拖板上的静刚度,m2是砂轮及其主轴系统的质量,k2是砂轮主轴支承在砂轮架轴承上的静刚度。
取每个质量的静平衡位置作为坐标原点,取其铅垂位移x1及x2分别作为各质量的独立坐标。
这样x1和x2就是用以确定磨头系统运动的广义坐标。
(工程实际中两自由度振动系统) [工程实例演示]§3-2 两自由度系统的自由振动一、系统的运动微分方程(①汽车动力学模型)②以图3.2的双弹簧质量系统为例。






第2次作业1.如图2-1所示,一小车(重P )自高h 处沿斜面滑下,与缓冲器相撞后,随同缓冲器一起作自由振动。
弹簧常数k ,斜面倾角为α,小车与斜面之间摩擦力忽略不计。
试求小车的振动周期和振幅。
hkαP答案:gkP T π2=,⎪⎭⎫ ⎝⎛+=α2sin 2k P h k P A图2-12.确定图2-2所示系统的固有频率。
圆盘质量为m 。
k kar Ox()2234mr a r k n +=ω图2-23.确定图2-3系统的固有频率。
()r R g n -=32ω图2-3第三章 两自由度系统振动§3-1 概述单自由度系统的振动理论是振动理论的基础。
在实际工程问题中,还经常会遇到一些不能简化为单自由度系统的振动问题,因此有必要进一步研究多自由度系统的振动理论。
两自由度系统是最简单的多自由度系统。
从单自由度系统到两自由度系统,振动的性质和研究的方法有质的不同。
研究两自由度系统是分析和掌握多自由度系统振动特性的基础。
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。
很多生产实际中的问题都可以简化为两自由度的振动系统。
例如,车床刀架系统(a )、车床两顶尖间的工件系统(b )、磨床主轴及砂轮架系统(c )。
只要将这些系统中的主要结合面(或芯轴)视为弹簧(即只计弹性,忽略质量),将系统中的小刀架、工件、砂轮及砂轮架等视为集中质量,再忽略存在于系统中的阻尼,就可以把这些系统近似简化成图(d)所示的两自由度振动系统的动力学模型。
以图3.1(c)所示的磨床磨头系统为例分析,因为砂轮主轴安装在砂轮架内轴承上,可以近似地认为是刚性很好的,具有集中质量的砂轮主轴系统支承在弹性很好的轴承上,因此可以把它看成是支承在砂轮架内的一个弹簧——质量系统。
此外,砂轮架安装在砂轮进刀拖板上,如果把进刀拖板看成是静止不动的,而把砂轮架与进刀拖板的结合面看成是弹簧,把砂轮架看成是集中的质量,则砂轮架系统又近似地可以看成是支承在进刀拖板上的另一个弹簧——质量系统。
二自由度系统的振动1.概述在实际工程中,真正的单自由度振动是很少的,而是根据需要将被研究对象简化成单自由度系统来研究。
但是许多问题不能简化为单自由度系统,为满足工程精度上的需要,必须按多自由度系统来研究。
一般讲,三自由度以上的系统要得到闭合解是相当困难的。
在这种情况下,可以用坐标变换的方法,将描述实际问题的广义坐标用一组新的坐标来代替。
新坐标所描述的系统运动方程与实际系统是相同的,但用新坐标描述的系统微分方程之间已不存在耦合,称为各自独立的微分方程,就可以按单自由度系统的微分方程那样一一单独求解。
这种新坐标主坐标或模态坐标。
二自由度系统是最简单的多自由度振动系统,许多多自由度喜用的物理概念及解题思路可以从二自由度系统的分析中得到启迪,也是分析多自由度系统的基础。
二自由度振动系统的结构具有两个固有频率。
当系统按其中某一固有频率作自由振动时,称之为主振动。
主振动是简谐振动。
当发生主振动时,描述振动的两个独立变量与振幅之间有确定的比例关系,即两个振幅比决定了整个系统的振动形态,称之为主振型。
任意初始条件下的自由振动一般是这两个不同频率的主振动的叠加,其叠加后的振动不一定是简谐振动。
当外界激扰为简谐激扰时,系统对其响应是与激扰频率相同的简谐振动。
当激扰频率接近系统的任意一固有频率时,就会发生共振。
共振时的振型就是与固有频率相对应的主振型。
此时,喜用的两个振动的振幅都趋于最大值。
2.二自由度系统的运动方程图1所示为具有粘性阻尼的二自由度系统。
图1.二自由度系统模型对质量m1、m2绘分离体图,如图2所示。
图2.二自由度系统分析图用牛顿第二定律分别列分离体在水平方向方程得:整理得:由两个联立二阶常微分方程所描述的系统统称为二自由度系统。
上述方程可以方便的表示成矩阵形式。
常数矩阵[m]、[c]和[k]分别为质量、阻尼、刚度矩阵。
{x(t)}和{F(t)}分别称为二维位移向量和力向量。
可以将上述方程写成矩阵形式:对于同一系统当采用不同的独立坐标系来描述时,其[m]、[c]、[k]矩阵中的元素是不同的,但不影响系统的固有特性,系统的固有频率与坐标的选取无关,一定的系统固有频率是一定的。
第三章 两自由度系统振动§3-1 概述单自由度系统的振动理论是振动理论的基础。
在实际工程问题中,还经常会遇到一些不能简化为单自由度系统的振动问题,因此有必要进一步研究多自由度系统的振动理论。
两自由度系统是最简单的多自由度系统。
从单自由度系统到两自由度系统,振动的性质和研究的方法有质的不同。
研究两自由度系统是分析和掌握多自由度系统振动特性的基础。
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。
很多生产实际中的问题都可以简化为两自由度的振动系统。
例如,车床刀架系统(a )、车床两顶尖间的工件系统(b )、磨床主轴及砂轮架系统(c )。
只要将这些系统中的主要结合面(或芯轴)视为弹簧(即只计弹性,忽略质量),将系统中的小刀架、工件、砂轮及砂轮架等视为集中质量,再忽略存在于系统中的阻尼,就可以把这些系统近似简化成图(d )所示的两自由度振动系统的动力学模型。
以图3.1(c )所示的磨床磨头系统为例分析,因为砂轮主轴安装在砂轮架内轴承上,可以近似地认为是刚性很好的,具有集中质量的砂轮主轴系统支承在弹性很好的轴承上,因此可以把它看成是支承在砂轮架内的一个弹簧——质量系统。
此外,砂轮架安装在砂轮进刀拖板上,如果把进刀拖板看成是静止不动的,而把砂轮架与进刀拖板的结合面看成是弹簧,把砂轮架看成是集中的质量,则砂轮架系统又近似地可以看成是支承在进刀拖板上的另一个弹簧——质量系统。
这样,磨头系统就可以近似地简化为图示的支承在进刀拖板上的两自由度系统。
在这一系统的动力学模型中,m 1是砂轮架的质量,k 1是砂轮架支承在进刀拖板上的静刚度,m 2是砂轮及其主轴系统的质量,k 2是砂轮主轴支承在砂轮架轴承上的静刚度。
取每个质量的静平衡位置作为坐标原点,取其铅垂位移x 1及x 2分别作为各质量的独立坐标。
这样x 1和x 2就是用以确定磨头系统运动的广义坐标。
(工程实际中两自由度振动系统) [工程实例演示]§3-2 两自由度系统的自由振动一、系统的运动微分方程(①汽车动力学模型)②以图3.2的双弹簧质量系统为例。
设弹簧的刚度分别为k 1和k 2,质量为m 1、m 2。
质量的位移分别用x 1和x 2来表示,并以静平衡位置为坐标原点,以向下为正方向。
(分析)在振动过程中的任一瞬间t ,m 1和m 2的位移分别为x 1及x 2。
此时,在质量m 1上作用有弹性恢复力()12211x x k x k -及,在质量m 2上作用有弹性恢复力()122x x k -。
这些力的作用方向如图所示。
应用牛顿运动定律,可建立该系统的振动微分方程式:()()⎭⎬⎫=-+=--+00122221221111x x k x m x x k x k x m &&&& (3.1) 令 2212121,,m k c m k b m k k a ==+=则(3.1)式可改写成如下形式: ⎭⎬⎫=+-=-+00212211cx cx x bx ax x &&&& (3.2) 这是一个二阶常系数线性齐次联立微分方程组。
(分析)在第一个方程中包含2bx -项,第二个方程中则包含1cx -项,称为“耦合项”(coupling term )。
这表明,质量m 1除受到弹簧k 1的恢复力的作用外,还受到弹簧 k 2的恢复力的作用。
m 2虽然只受一个弹簧k 2恢复力的作用,但这一恢复力也受到第一质点m 1位移的影响。
我们把这种位移之间有耦合的情况称为弹性耦合。
若加速度之间有耦合的情况,则称之为惯性耦合。
二、固有频率和主振型[创造思维:]从单自由度系统振动理论得知,系统的无阻尼自由振动是简谐振动。
我们也希望在两自由度系统无阻尼自由振动中找到简谐振动的解。
因此可先假设方程组(3.2)式有简谐振动解,然后用待定系数法来寻找有简谐振动解的条件。
设在振动时,两个质量按同样的频率和相位角作简谐振动,故可设方程组(3.2)式的特解为:()()⎭⎬⎫+=+=ϕωϕωt A x t A x n n sin sin 2211 (3.3) 其中振幅A 1与A 2、频率n ω、初相位角ϕ都有待于确定。
对(3.3)式分别取一阶及二阶导数: ()()()()⎪⎭⎪⎬⎫+-=+=+-=+=ϕωωϕωωϕωωϕωωt A x t A x t A x t A x n n n n n n n n sin ;cos sin ;cos 2222221111&&&&&&(3.4)将(3.3)、(3.4)式代入(3.2)式,并加以整理后得: ()()⎪⎭⎪⎬⎫=-+-=--00221212A c cA bA A a n n ωω (3.5) 上式是A 1、A 2的线性齐次代数方程组。
A 1、A 2=0显然不是我们所要的振动解,要使A 1、A 2有非空解,则(3.5)式的系数行列式必须等于零,即: 22n n c cba ωω---- = 0将上式展开得: ()()024=-++-b a c c a n n ωω (3.6)解上列方程,可得如下的两个根: ()bc c a c a b a c c a c a n +⎪⎭⎫ ⎝⎛-+=--⎪⎭⎫ ⎝⎛++=2222,12222μμω (3.7)由此可见,(3.6)式是决定系统频率的方程,故称为系统的频率方程(frequency equation )或特征方程(characteristic equation )。
特征方程的特征值(characteristic value )即频率n ω只与参数a ,b ,c 有关。
而这些参数又只决定于系统的质量m 1,m 2和刚度k 1,k 2,即频率n ω只决定于系统本身的物理性质,故称n ω为系统的固有频率。
两自由度系统的固有频率有两个,即12121n n n n n ωωωωω,把,且和<称为第一阶固有频率(first order natural circular frequency )。
[基频]2n ω称为第二阶固有频率(second order natural circular frequency )。
[(推广)理论证明,n 个自由度系统的频率方程是2n ω的n 次代数方程,在无阻尼的情况下,它的n 个根必定都是正实根,故主频率的个数与系统的自由度数目相等。
]将所求得的1n ω和2n ω代入(3.5)式中得:()()()()⎪⎪⎭⎪⎪⎬⎫-=-==-=-==222221222212111121n n n n c c b a A A c c b a A A ωωβωωβ (3.8) 式中:()()1211,A A ——对应于1n ω的质点m 1,m 2的振幅; ()()2221,A A ——对应于2n ω的质点m 1,m 2的振幅。
由此可见,对应于1n ω和2n ω,振幅A 1与A 2之间有两个确定的比值。
称之为振幅比(amplitude ratio )。
将(3.8)式与(3.3)式联系起来可以看出,两个m 1与m 2任一瞬间位移的比值12x x 。
系统的其它点的位移都可以由x 1及x 2来决定。
这样,在振动过程中,系统各点位移的相对比值都可以由振幅比确定,也就是振幅比决定了整个系统的振动形态。
因此,我们将振幅比称为系统的主振型(principal mode ),也可称为固有振型(natural mode )。
其中:1β——第一主振型,即对应于第一主频率1n ω的振幅比;2β——第二主振型,即对应于第二主频率2n ω的振幅比。
*当系统以某一阶固有频率按其相应的主振型作振动时,即称为系统的主振动(principal vibration )。
所以,第一主振动为:()()()()()()()()⎪⎭⎪⎬⎫+=+=+=11111111212111111sin sin sin ϕωβϕωϕωt A t A x t A x n n n (3.9) 第二主振动为:()()()()()()()()⎪⎭⎪⎬⎫+=+=+=22212222222222121sin sin sin ϕωβϕωϕωt A t A x t A x n n n (3.10) 为了进一步研究主振型的性质,可以将(3.7)式改写成如下形式:因为 bc c a c a n -⎪⎭⎫ ⎝⎛-+=222,122μω 因为上式的等式右边恒大于零,所以021>-n a ω,由(3.8)式知,01>β因为上式的等式右边恒小于零,所以022<-n a ω,由(3.8)式知,02<β。
(说明)由此可见,01>β表示()()1211A A 和的符号相同,即第一主振动中两个质点的相位相同。
因此,若系统按第一主振型进行振动的话,两个质点就同时向同方向运动,它们同时经过平衡位置,又同时达到最大偏离位置。
而02<β,则表示第二主振动中两个质点的相位相反,永远相差180°。
当质量m 1到达最低位置时,质量m 2恰好到达最高位置。
它们一会相互分离,一会又相向运动,这样,在整个第二主振动的任一瞬间的位置都不改变。
这样的点称为“节点”(nodal point )。
振动理论证明,多自由度系统的i 阶主振型一般有i -1个节点。
这就是说,高一阶的主振型就比前一阶主振型多一个节点。
阶次越高的主振动,节点数就越多,故其相应的振幅就越难增大。
相反,低阶的主振动由于节点数少,故振动就容易激起。
所以,在多自由度系统中,低频主振动比高频主振动危险。
三、系统对初始条件的响应[思维方式:]前面分析了两自由度系统的主振动,而这些主振动又都是简谐振动。
但两自由度系统在受到干扰后出现的自由振动究竟是什么形式呢?这要取决于初始条件。
从微分方程的理论来说,两阶主振动只是微分方程组的两组特解。
而它的通解则应由这两组特解相叠加组成。
从振动的实践来看,两自由度系统受到任意的初干扰时,一般来说,系统的各阶主振动都要激发。
因而出现的自由振动应是这些简谐振动的合成。
所以,在一般的初干扰下,系统的响应是:()()()()()()()()⎪⎭⎪⎬⎫+++=+++=22212111112222111111sin sin sin sin ϕωβϕωβϕωϕωt A t A x t A t A x n n n n (3.11)式中,()()212111,ϕϕ,,A A 四个未知数要由振动的四个初始条件来决定。
设初始条件为:t=0时,202101202101,,,x x x x x x x x &&&&====经过运算,可以求出: ()()()()()()⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪⎬⎫--=--=⎪⎪⎭⎫ ⎝⎛-+--=⎪⎪⎭⎫ ⎝⎛-+--=--20101201012122010220102111222010122010121.212120102220102121111x x x x tg x x x x tg x x x x A x x x x A n n n n &&&&&&&&&&&&ββωϕββωϕωββββωββββ (3.12) 将(3.12)式代入(3.11)就得到系统在上述初始下响应。