机械振动二自由度讲解
- 格式:ppt
- 大小:1.67 MB
- 文档页数:29



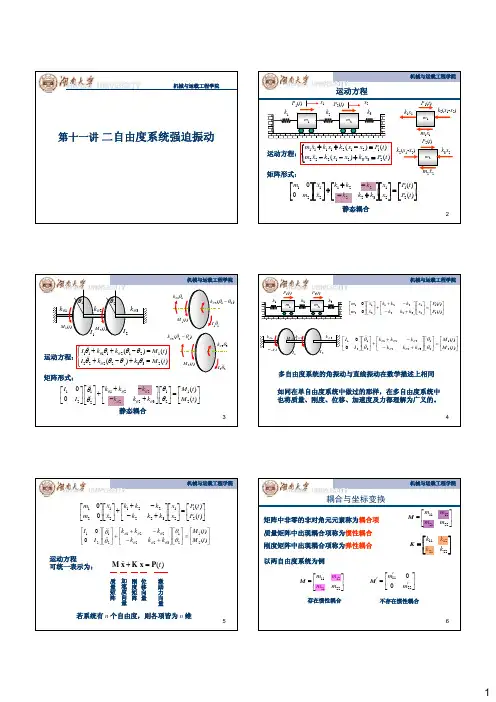
机械与运载工程学院第十一讲二自由度系统强迫振动2机械与运载工程学院运动方程m 1m 2k 3k 1k 2x 1x 2P 1(t )P 2(t )k 1x 1k 2(x 1-x 2)11x m m 1P 2(t )k 2(x 1-x 2)22xm m 2k 3x 2⎩⎨⎧=+−−=−++)()()()(2332122212121111t P x k x x k x m t P x x k x k x m 运动方程:矩阵形式:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+−−++⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡)()(0021213222212121t P t P x x k k k k k k x x m m3机械与运载工程学院1θk 1I 2θ2I 2θk 3θk )(1t M )(2t M 1θ11θθk 11θ I )(1t M )(212θθθ−k 22θ I )(2t M 33θθk )(122θθθ−k 1111121212222332()()()()I k k M t I k k M t θθθθθθθθθθθ⎧++−=⎪⎨+−+=⎪⎩运动方程:矩阵形式:122111122322220()0()k k k I M t k k k I M t θθθθθθθθθθ+−⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥−+⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ 4机械与运载工程学院⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+−−++⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡)()(0021213222212121t P t Px x k k k k k k x x m m⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+−−++⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡)()(0021213222212121t M t M k k k k k k I I θθθθθθθθθθ 多自由度系统的角振动与直线振动在数学描述上相同如同在单自由度系统中做过的那样,在多自由度系统中也将质量、刚度、位移、加速度及力都理解为广义的。



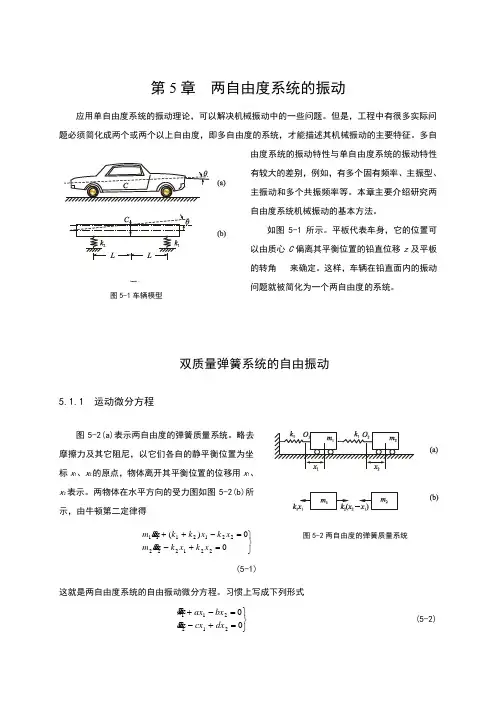
第5章 两自由度系统的振动应用单自由度系统的振动理论,可以解决机械振动中的一些问题。
但是,工程中有很多实际问题必须简化成两个或两个以上自由度,即多自由度的系统,才能描述其机械振动的主要特征。
多自由度系统的振动特性与单自由度系统的振动特性有较大的差别,例如,有多个固有频率、主振型、主振动和多个共振频率等。
本章主要介绍研究两自由度系统机械振动的基本方法。
如图5-1所示。
平板代表车身,它的位置可以由质心C 偏离其平衡位置的铅直位移z 及平板的转角 来确定。
这样,车辆在铅直面内的振动问题就被简化为一个两自由度的系统。
双质量弹簧系统的自由振动5.1.1 运动微分方程图5-2(a)表示两自由度的弹簧质量系统。
略去摩擦力及其它阻尼,以它们各自的静平衡位置为坐标x 1、x 2的原点,物体离开其平衡位置的位移用x 1、x 2表示。
两物体在水平方向的受力图如图5-2(b)所示,由牛顿第二定律得 ⎭⎬⎫=+-=-++00)(2212222212111x k x k x m x k x k k x m &&&&(5-1)这就是两自由度系统的自由振动微分方程。
习惯上写成下列形式⎭⎬⎫=+-=-+00212211dx cx x bx ax x &&&& (5-2)图5-1车辆模型图5-2两自由度的弹簧质量系统显然此时2212121,,m k d c m k b m k k a ===+=但对不同的系统, 式(5-2)中各系数的意义并不相同。
5.1.2 固有频率和主振型根据微分方程的理论,设方程(5-2)的解,即两自由度无阻尼自由振动系统的解为⎪⎭⎪⎬⎫+=+=)sin()sin(2211ααpt A x pt A x(5-3)或写成以下的矩阵形式)sin(2121α+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧pt A A x x (5-4)将式(5-4)代入式(5-2),可得代数齐次方程组⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡----002122A A p d c b p a (5-5)保证式(5-5)具有非零解的充分必要条件是式(5-5)的系数行列式等于零,即0)(222=----=∆p d cbp a p展开后为0)(24=-++-bc ad p d a p(5-6)式(5-6)唯一确定了频率p 满足的条件,通常称为频率分程或特征方程。


机械振动大作业姓名:徐强学号:SX1302106专业:航空宇航推进理论与工程能源与动力学院2013年12月简支梁的振动特性分析题目:针对简支梁、分别用单、双、三、十个自由度以及连续体模型,计算其固有频率、固有振型。
单、双、三自由度模型要求理论解;十自由度模型要求使用李兹法、霍尔茨法、矩阵迭代法、雅可比法、子空间迭代法求解基频;连续体要求推导理论解,并通过有限元软件进行数值计算。
解答:一、 单自由度简支梁的振动特性如图1,正方形截面(取5mm ×5mm )的简支梁,跨长为l =1m ,质量m 沿杆长均匀分布,将其简化为单自由度模型,忽略阻尼,则运动微分方程为0=+••kx x m ,固有频率ωn =eqeq m k ,其中k 为等效刚度,eq m 为等效质量。
因此,求出上述两项即可知单自由度简支梁的固有频率。
根据材料力学的结果,由于横向载荷F 作用在简支梁中间位置而引起的变形为)(224348EI F -)(x l x x y -=(20l x ≤≤), 48EI F -3max l y =为最大挠度,则: eq k =δF=348EIl 梁本身的最大动能为:)(224348EI F -)(x l x x y -==)(223max43x l lx y -T max =2×dx x y l m l 220)(21⎭⎬⎫⎩⎨⎧•⎰=2max 351721•y m )( 如果用eq m 表示简支梁的质量等效到中间位置时的大小,它的最大动能可表示为:T max =2max21•y m eq所以质量为m 的简支梁,等效到中间位置的全部质量为: m m eq 3517=故单自由度简支梁横向振动的固有频率为:ωn =eqeq m k =3171680ml EImk图1 简支梁的单自由度模型二、 双自由度简支梁的振动特性如图2,将简支梁简化为双自由度模型,仍假设在简支梁中间位置作用载荷,根据对称性,等效质量相等,因此只要求出在3/l 处的等效质量即可。
第五章两自由度系统振动§5-1 概述单自由度系统的振动理论是振动理论的基础。
在实际工程问题中,还经常会遇到一些不能简化为单自由度系统的振动问题,因此有必要进一步研究多自由度系统的振动理论。
两自由度系统是最简单的多自由度系统。
从单自由度系统到两自由度系统,振动的性质和研究的方法有质的不同。
研究两自由度系统是分析和掌握多自由度系统振动特性的基础。
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。
很多生产实际中的问题都可以简化为两自由度的振动系统。
①汽车动力学模型:图3.1两自由度汽车动力学模型§5-2 两自由度系统的自由振动一、系统的运动微分方程②以图3.2的双弹簧质量系统为例。
设弹簧的刚度分别为k 1和k 2,质量为m 1、m 2。
质量的位移分别用x 1和x 2来表示,并以静平衡位置为坐标原点,以向下为正方向。
(分析)在振动过程中的任一瞬间t ,m 1和m 2的位移分别为x 1及x 2。
此时,在质量m 1上作用有弹性恢复力()12211x x k x k -及,在质量m 2上作用有弹性恢复力()122x x k -。
这些力的作用方向如图所示。
应用牛顿运动定律,可建立该系统的振动微分方程式:()()⎭⎬⎫=-+=--+00122221221111x x k x m x x k x k xm (3.1)令2212121,,m k c m k b m k k a ==+=则(3.1)式可改写成如下形式:()()⎭⎬⎫=-+=--+00122221221111x x k x m x x k x k xm⎭⎬⎫=+-=-+00212211cx cx xbx ax x(3.2) 这是一个二阶常系数线性齐次联立微分方程组。
(分析)在第一个方程中包含2bx -项,第二个方程中则包含1cx -项,称为“耦合项”(coupling term )。
这表明,质量m 1除受到弹簧k 1的恢复力的作用外,还受到弹簧 k 2的恢复力的作用。
二自由度动力学模型
二自由度动力学模型是一种广泛应用于机械工程、随机振动控制等领域的数学模型,由于其简单清晰的结构和易于求解的特点,成为了研究系统动力学特性的重要工具。
本文将详细介绍二自由度动力学模型的相关知识和应用方法。
一、什么是二自由度动力学模型?
二自由度动力学模型是指一个由两个质点通过弹簧和阻尼器连接而成的物理系统,其中每个质点只能沿一个方向(通常是水平和垂直方向)运动。
该模型的动力学特性可以描述为一个二阶非齐次线性微分方程组,其中包含了质点的运动方程和能量守恒方程。
二、如何建立二自由度动力学模型?
建立二自由度动力学模型需要以下步骤:
1、绘制系统结构示意图,包括两个质点、弹簧和阻尼器的连接方式。
2、确定系统的自由度,即质点可以进行的运动方向。
3、根据受力分析和牛顿第二定律,建立质点的运动方程。
4、利用能量守恒原理,建立能量守恒方程。
5、将质点的运动方程和能量守恒方程组合起来,得到二阶非齐次线性微分方程组。
6、利用数值解或解析解的方法,求解微分方程组,得到系统的运动特性。
三、二自由度动力学模型的应用
二自由度动力学模型广泛应用于机械工程、随机振动控制等领域,是许多控制系统的核心部分。
具体应用包括:
1、建立机械振动控制系统的模型,分析系统的稳定性和响应特性,优化控制策略。
2、研究结构物的振动特性,评估地震对建筑物的影响,提高建筑结构的抗震性能。
3、分析风力发电机、桥梁等大型结构的振动特性,提高其安全性和稳定性。
总之,二自由度动力学模型是一种非常重要和有用的工具,可以用于解决各种动力学问题,为实际应用提供了有效的支持。
第四章两自由度系统的振动当振动系统需要两个独立坐标描述其运动时,称为两自由度振动系统。
两自由度系统是最简单的多自由度系统,因此研究两自由度系统是分析和掌握多自由度系统的基础。
两自由度系统具有两个固有频率,两自由度系统以固有频率进行的振动与单自由度系统不同,它以固有频率进行的振动是指整个系统在运动过程中莫一位移形状,称为固有振型,因此两自由度具有两个与固有频率对应的两个固有振型。
在任意初始条件下的自由振动响应一般由两个固有振型的叠加得到。
受迫简谐振动的频率与激励频率相同。
两自由度系统的振动微分方程一般由两个联立的微分方程组成。
如果恰当地选取坐标,可使两个微分方程解除耦合,这种坐标称为主坐标或固有坐标。
用固有坐标建立的系统振动微分方程为两个独立的单自由度系统的微分方程。
4.1系统的自由振动如图所示的无阻尼两质量-弹簧系统,可沿光滑水平面滑动的两个质量与分别用弹簧与连至定点,并用弹簧相互连接。
三个弹簧的轴线沿同一水平线,质量与只限于沿着该直线进行往复运动。
这样与的任一瞬时的位置只需用坐标与就可以完全确定,因此该系统具有两个自由度。
图两自由度系统的振动取与的静平衡位置为坐标原点。
在振动过程中任一瞬时t,与的位置分别为与,作用于与的重力于光滑水平面的法向反力相平衡,在质量的水平方向作用有弹性恢复力和,质量的水平方向则受到和作用,方向如图所示。
取加速度和力的正方向与坐标正方向一致,根据牛顿运动定律有移项得方程()就是图所示的两自由度系统自由振动的微分方程,为二阶常系数线性齐次常微分方程组。
方程()可以使用矩阵形式来表示,写成由系数矩阵组成的常数矩阵m和k分别称为质量矩阵和刚度矩阵,向量x 称为位移向量。
因此设分别为刚度矩阵k中的元素,因而方程()可以写成方程()为系统自由振动的微分方程。
方程()是齐次的,如果和位方程()的一个解,那么与其相差一个因子的和也将是一个解。
通常感兴趣的是一种特殊形式的解,也就是和同步运动的解。