用MATLAB画零极点图
- 格式:ppt
- 大小:155.50 KB
- 文档页数:14

电源零极点 matlab介绍在电力系统中,电源是一个重要的组成部分,它为电力设备提供所需的电能。
电源的性能直接影响到电力系统的稳定性和可靠性。
为了更好地了解电源的特性和行为,我们可以使用Matlab来进行分析和模拟。
什么是零极点在电源的分析中,零极点是非常重要的概念。
零点是电源传递函数中使得输出为零的输入值,而极点则是使得传递函数无穷大的输入值。
了解电源的零极点分布可以帮助我们更好地理解电源的频率响应和稳定性。
使用Matlab分析电源的零极点Matlab是一个功能强大的数学计算软件,它提供了丰富的工具和函数来进行电源的分析。
以下是使用Matlab分析电源零极点的一般步骤:1. 定义电源传递函数首先,我们需要定义电源的传递函数。
传递函数是描述输入和输出之间关系的数学表达式。
在Matlab中,可以使用tf函数来定义传递函数。
例如,如果我们有一个传递函数为s/(s+1)的电源,可以使用以下代码进行定义:num = [1];den = [1, 1];sys = tf(num, den);2. 绘制零极点图接下来,我们可以使用zpk函数来获取电源的零极点信息,并使用zplane函数来绘制零极点图。
零极点图可以帮助我们直观地了解电源的频率响应和稳定性。
以下是绘制零极点图的代码示例:[z, p, k] = zpkdata(sys);zplane(z, p);3. 分析零极点的位置和数量通过观察零极点图,我们可以分析电源的零极点的位置和数量。
零极点的位置可以告诉我们电源的频率响应特性,而零极点的数量则与电源的稳定性相关。
通常情况下,零极点越远离原点,电源的频率响应越宽,但稳定性可能会受到影响。
4. 评估电源的稳定性除了通过零极点图来评估电源的稳定性外,我们还可以使用Matlab提供的稳定性分析工具来进行评估。
Matlab提供了一些函数,如isstable和margin,可以帮助我们快速评估电源的稳定性。
以下是使用isstable函数来评估电源稳定性的代码示例:isStable = isstable(sys);5. 优化电源设计根据对电源零极点的分析和评估结果,我们可以进一步优化电源的设计。
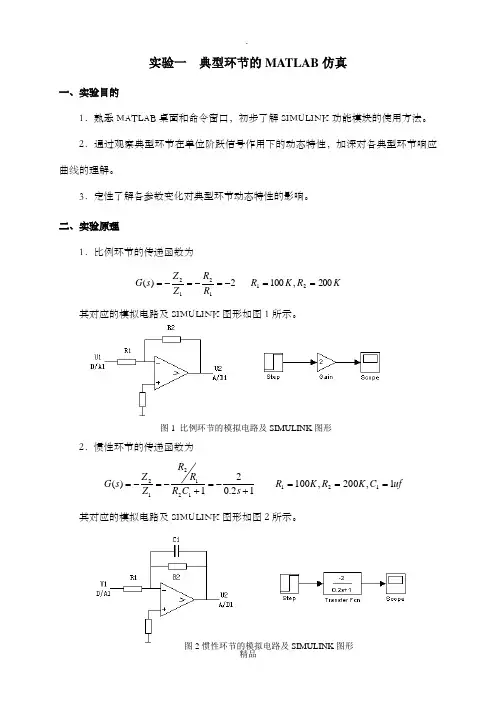
实验一 典型环节的MATLAB 仿真一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验原理1.比例环节的传递函数为 K R K R R R Z ZsG 200,1002)(211212==-=-=-=其对应的模拟电路及SIMULINK 图形如图1所示。
2.惯性环节的传递函数为uf C K R K R s C R R R Z Z s G 1,200,10012.021)(121121212===+-=+-=-=其对应的模拟电路及SIMULINK 图形如图2所示。
图1 比例环节的模拟电路及SIMULINK 图形3.积分环节(I)的传递函数为uf C K R s s CR Z Z s G 1,1001.011)(111112==-=-=-=其对应的模拟电路及SIMULINK 图形如图3所示。
4.微分环节(D)的传递函数为uf C K R s s C R Z Z s G 10,100)(111112==-=-=-= uf C C 01.012=<<其对应的模拟电路及SIMULINK 图形如图4所示。
5.比例+微分环节(PD )的传递函数为)11.0()1()(111212+-=+-=-=s s C R R R Z Z s G uf C C uf C K R R 01.010,10012121=<<===其对应的模拟电路及SIMULINK 图形如图5所示。
图3 积分环节的模拟电路及及SIMULINK 图形图4 微分环节的模拟电路及及SIMULINK 图形6.比例+积分环节(PI )的传递函数为 )11(1)(11212sR s C R Z Z s G +-=+-=-= uf C K R R 10,100121=== 其对应的模拟电路及SIMULINK 图形如图6所示。

matlab zplane函数用法
`zplane`是MATLAB中用于绘制数字滤波器零极点图的函数。
以下是关于`zplane`函数的一些基本用法:
```matlab
%语法:
zplane(b,a)
%示例:
b=[1,-1];%分子多项式系数
a=[1,-0.5];%分母多项式系数
zplane(b,a)
title('零极点图')%添加图的标题
xlabel('实部')%添加x轴标签
ylabel('虚部')%添加y轴标签
```
这里,`b`是数字滤波器的分子多项式系数,`a`是数字滤波器的分母多项式系数。
`zplane`函数会绘制这些系数所对应的零极点图。
-`b`和`a`的系数是多项式的系数,例如,`[1,-1]`对应于多项式`1-z^(-1)`。
-在零极点图中,零点用"o"表示,极点用"x"表示。
-通过在`zplane`函数后面添加标题和轴标签,可以使图更具可读性。
此外,你还可以使用其他参数和选项来调整图的外观。
可以通过输入`help zplane`来查看更多详细的用法和选项。

《数字信号处理》(一) 实验目的使用ztrans,iztrans 函数分别求出离散时间信号的Z 变换和Z 反变换的结果,并用pretty 函数进行结果美化。
编写函数时养成良好的注释习惯,有利于对函数的理解。
复习MATLAB 的基本应用,如:help,可以帮助查询相关的函数的使用方法,巩固理论知识中的离散时间信号的传递函数与二次项式之间的转换,以及使用zplane 函数画出相关系统的零极点分布图,根据零极点的分布情况估计系统的滤波特性。
(二) 程序的运行与截图实验项目一Z 变换(1)求)(])31()21[()(n u n x nn += Z 变换clear all;close all;clc;syms nf=0.5^n+(1/3)^n; %定义离散信号F=ztrans(f) %z 变换pretty(F); 运算结果F(2)4)(n n x = Z 变换clear all ;close all ;clc;syms nf=n^4; %定义离散信号F=ztrans(f) %Z 变换 pretty(F)运算结果(3))sin()(b an n x += Z 变换clear all;close all;clc;syms a b nf = sin(a*n+b) %定义离散信号F=ztrans(f) %Z 变换pretty(F)运算结果实验项目二Z 反变换(1)2)2(2)(-=z z z X Z 反变换 clear all;close all;clc;syms k zFz=2*z/(z-2)^2; %定义Z 反变换表达式fk=iztrans(Fz,k) %Z 反变换pretty(fk);运算结果(2)12)1()(2++-=z z z z z X Z 反变换 clear all;close all;clc;syms k zFz=z*(z-1)/(z^2+2*z+1); %定义Z 反变换表达式fk=iztrans(Fz,k) %Z 反变换pretty(fk);运算结果f(3) 211cos 211)(---+-+=zz z z X ω Z 反变换 clear all;close all;clc;syms k z wFz=(1+z^(-1))/(1-2*z^-1*cos(w)+z^-2); %定义Z 反变换表达式fk=iztrans(Fz,k) %Z 反变换pretty(fk);运算结果实验项目三各种模型之间的变换2)2)(1(10)(--=z z z z H =4851023-+-z z z z (1)clear all;close all;clc;b=[0 0 10 0];%分子的系数数组a=[1 -5 8 -4]; %分母的系数数组zplane(b,a)% 使用zplane 函数绘制如下系统的零极点分布图 运算结果(2)clear all ;close all ;clc;b=[0 0 10 0]; %分子的系数数组a=[1 -5 8 -4]; %分母的系数数组[r,p,c]=residuez(b,a) %使用matlab 中的residuez 函数,将)(z H 分解成为多个简单有理分式之和运算结果r =-15.00005.000010.0000p =2.00002.00001.0000c =(3)clear all;close all;clc;b=[0 0 10 0]; %分子的系数数组a=[1 -5 8 -4]; %分母的系数数组[z,p,k]=tf2zp(b,a) %使用tf2zp求出系统函数的零、极点和增益运算结果z =p =2.00002.00001.0000k =10(4)clear all;close all;clc;z=[1;-3];%零点,列向量p=[2; -4];%极点,列向量k=5; %增益[b,a] = zp2tf(z,p,k) %根据求出的零、极点和增益,然后自学使用zp2tf还原出分子和分母的系数运算结果(5)clear all;close all;clc;b=[0 0 10 0]; %分子的系数数组a=[1 -5 8 -4]; %分母的系数数组[sos,g]=tf2sos(b,a) %使用tf2sos将系统函数分解成一系列二阶子系统的级联形式运算结果sos =0 1.0000 0 1.0000 -2.0000 00 1.0000 0 1.0000 -3.0000 2.0000g =10(6)clear all;close all;clc;sos=[0 1.0000 0 1.0000 -2.0000 0;0 1.0000 0 1.0000 -3.0000 2.0000];g=10;%增益[b,a]=sos2tf(sos,g) %根据求出的一系列二阶子系统,使用sos2tf还原出H分子和分母的系数)(z运算结果b =0 0 10 0a =1 -5 8 -4(7)clear all;close all;clc;b=[0 0 10 0]; %分子的系数数组a=[1 -5 8 -4]; %分母的系数数组n=(0:500)*pi/500; %在pi范围内取501个采样点[h,w]=freqz(b,a,n);%求系统的频率响应subplot(2,1,1),plot(n/pi,abs(h));grid %作系统的幅度频响图axis([0,1,1.1*min(abs(h)),1.1*max(abs(h))]);ylabel(‘幅度’);subplot(2,1,2),plot(n/pi,angle(h));grid %作系统的相位频响图axis([0,1,1.1*min(angle(h)),1.1*max(angle(h))]);ylabel(‘相位’);xlabel(‘以pi为单位的频率’);运行结果2221)(232+++++=z z z z z z H (1)clear all ;close all ;clc;b=[0 1 1 1]; %分子的系数数组a=[1 2 2 2]; %分母的系数数组zplane(b,a)% 使用zplane 函数绘制如下系统的零极点分布图运行结果(2)clear all ;close all ;clc;b=[0 1 1 1]; %分子的系数数组a=[1 2 2 2]; %分母的系数数组[r,p,k]=residuez(b,a) %使用matlab 中的residuez 函数,将)(z H 分解成为多个简单有理分式之和运行结果r =-0.4006-0.0497 - 0.1609i-0.0497 + 0.1609ip =-1.5437-0.2282 + 1.1151i-0.2282 - 1.1151ik =0.5000(3)clear all;close all;clc;b=[0 1 1 1]; %分子的系数数组a=[1 2 2 2]; %分母的系数数组[z,p,k]=tf2zp(b,a) %使用tf2zp求出系统函数的零、极点和增益运行结果z =-0.5000 + 0.8660i-0.5000 - 0.8660ip =-1.5437-0.2282 + 1.1151i-0.2282 - 1.1151ik =1(4)clear all;close all;clc;z=[-0.5000 + 0.8660i-0.5000 - 0.8660i];p=[-1.5437-0.2282 + 1.1151i-0.2282 - 1.1151i ];k=1;[b,a]=zp2tf(z,p,k) %根据求出的零、极点和增益,使用zp2tf 还原出)(z H 分子和分母的系数运行结果b =0 1.0000 1.0000 1.0000a =1.00002.0001 2.0001 1.9999(5)clear all ;close all ;clc;b=[0 1 1 1]; %分子的系数数组a=[1 2 2 2]; %分母的系数数组[sos,g]=tf2sos(b,a) %使用tf2sos 将系统函数分解成一系列二阶子系统的级联形式运行结果sos =0 1.0000 0 1.0000 1.5437 01.0000 1.0000 1.0000 1.0000 0.4563 1.2956g =1(6)clear all ;close all ;clc;sos=[ 0 1.0000 0 1.0000 1.5437 0;1.0000 1.0000 1.0000 1.0000 0.4563 1.2956];g=1;[b,a]=sos2tf(sos,g) %根据求出的一系列二阶子系统,自学使用sos2tf 还原出)(z H 分子和分母的系数运行结果b =0 1 1 1a =1.00002.0000 2.0000 2.0000(7)clear all;close all;clc;b=[0 1 1 1]; %分子的系数数组a=[1 2 2 2]; %分母的系数数组n=(0:500)*pi/500; %在pi范围内取501个采样点[h,w]=freqz(b,a,n);%求系统的频率响应subplot(2,1,1),plot(n/pi,abs(h));grid %作系统的幅度频响图axis([0,1,1.1*min(abs(h)),1.1*max(abs(h))]);ylabel('幅度');subplot(2,1,2),plot(n/pi,angle(h));grid %作系统的相位频响图axis([0,1,1.1*min(angle(h)),1.1*max(angle(h))]);ylabel('相位');xlabel('以pi为单位的频率');运行结果实验项目四根据零极点分布图估计系统的滤波特性。

第一章1-1 有一个连续信号)2cos()(ψπ+=ft t x a ,式中Hz f 20=,2πψ=,(1) 求出)(t x a 的周期;(2) 用采样间隔s T 02.0=对)(t x a 进行采样,写出采样信号)(ˆt xa 的表达式; (3) 画出对应)(ˆt xa 的时域离散信号(序列))(n x 的波形,并求出)(n x 的周期。
解:(1))(t x a 的周期是s fT a 05.01==(2)∑∞-∞=-+=n a nT t fnT t x)()2cos()(ˆδψπ∑∞-∞=-+=n nT t nT )()40cos(δψπ(3))(n x 的数字频率为πω8.0=,252=ωπ周期5=N 。
)28.0cos()(ππ+=n n x ,画出其波形如题1-1图所示。
题1-1图 1-2 设)sin()(t t x a π=,()()sin()a s s x n x nT nT π==,其中s T 为采样周期。
(1))(t x a 信号的模拟频率Ω为多少? (2)Ω和ω的关系是什么?(3)当s T s 5.0=时,)(n x 的数字频率ω为多少? 解:(1))(t x a 的模拟频率s rad /π=Ω。
(2)Ω和ω的关系是:s T ⋅Ω=ω。
(3)当s T s 5.0=时,rad πω5.0=。
1-3 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1))873cos()(ππ-=n A n x ,A 为常数;(2))81()(π-=n j e n x 。
解: (1)πω73=,3142=ωπ,这是有理数,因此是周期序列,周期是14=T ; (2)81=ω,πωπ162=,这是无理数,因此是非周期序列。
1-4 研究一个线性时不变系统,其单位脉冲响应为指数序列)()(n u a n h n =,10<<a 。
对于矩阵输入序列,1,01()0N n N R n ≤≤-⎧=⎨⎩,其他 求出输出序列,并用MA TLAB 计算,比较其结果。






matlab传递函数零极点模型
Matlab传递函数零极点模型是一种用于描述系统动态行为的模型。
它可以用来描述系统的输入和输出之间的关系,以及系统的响应特性。
Matlab传递函数零极点模型是一种线性模型,它可以用来描述系统的动态行为,包括系统的输入和输出之间的关系,以及系统的响应特性。
Matlab传递函数零极点模型的基本原理是,系统的输入和输出之间存在一个线性关系,即输出可以用输入的线性组合来表示。
这种线性关系可以用一个传递函数来表示,它由一个零极点和一个极点组成。
零极点表示系统的输入和输出之间的线性关系,而极点表示系统的响应特性。
Matlab传递函数零极点模型可以用来描述系统的动态行为,包括系统的输入和输出之间的关系,以及系统的响应特性。
它可以用来模拟系统的行为,以及预测系统的响应。
此外,Matlab传递函数零极点模型还可以用来设计控制系统,以改善系统的性能。
Matlab传递函数零极点模型是一种有用的工具,可以用来描述系统的动态行为,以及预测系统的响应。
它可以用来模拟系统的行为,以及设计控制系统,以改善系统的性能。
此外,Matlab传递函数零极点模型还可以用来分析系统的稳定性,以及系统的响应特性。
因此,Matlab传递函数零极点模型是一种有用的工具,可以用来描述系统的动态行为,以及预测系统的响应。
matlab与信号系统实验题库(1)1.设,试⽤MATLAB画出该系统的幅频特性和相频特性。
w=0:0.025:15;b=[1];a=[0.08,0.4,1];H=freqs(b,a,w);subplot(2,1,1);plot(w,abs(H));grid;title('H(jw)的幅频特性');subplot(2,1,2);plot(w,angle (H));grid;title('H(jw)的相频特性');2. 绘制出y(t)=ε(t-1)- ε(t-4)的幅频特性曲线。
syms t wGt=sym('heaviside(t-1)-heaviside(t-4)');Fw=fourier(Gt,t,w);FFw=maple('convert',Fw,'piecewise');FFP=abs(FFw);ezplot(FFP,[-10*pi 10*pi]);grid;axis([-10*pi 10*pi 0 3.5])3.若某连续系统的输⼊为e(t),输出为r(t),系统的微分⽅程为:,y’(0_)=5,y(0_)=0;,求全响应。
a=[1 5 6];b=[0 3 2];%定义a,b[A B C D]=tf2ss(b,a);%定义A,B,C,,D的返回值t=0:0.01:5;%定义时间范围f=exp(-2*t); %定义函数X0=[5,0];%系统状态变量X=[x1,x2,…..xn]'在t=0时刻的初值。
xlabel('t');%定义横标题title('全响应y(t)');%定义总横标题grid on;%⽹格4.求的拉⽒变换式,并⽤MATLAB绘制拉⽒变换在s平⾯的三维曲⾯图。
syms t s %定义符号变量ft=sym('2*exp(-t)*Heaviside(t)+5*exp(-3*t)*Heaviside(t)'); %定义时间函数f(t)的表达式Fs=laplace(ft) %求f(t)的拉⽒变换式F(s)FFss=abs(Fs); %求出F(s)的模ezmesh(FFss); %画出拉⽒变换的⽹格曲⾯图ezsurf(FFss); %画出带阴影效果的三维曲⾯图colormap(hsv); %设置图形中多条曲线的颜⾊顺序5.求的拉⽒变换式,并⽤MATLAB绘制拉⽒变换在s平⾯的三维曲⾯图。
题 目: 用MATLAB 进行控制系统的动态性能的分析 初始条件:已知三阶系统的闭环传递函数为)64.08.0)(11(7.2)(2+++=s s s as G分析系统的动态性能。
要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、用MATLAB 函数编程,求系统的动态性能指标。
2、设64.08.02++s s 的根是系统的主导极点,编制程序,求系统的动态性能指标。
3、用MATLAB 编制程序分析a =0.84,a =2.1,a =4.2系统的阶跃响应曲线,分析高阶系统忽略附加极点,近似为二阶系统的条件。
4、课程设计说明书中要求写清楚计算分析的过程,列出MATLAB 程序和MATLAB 输出。
说明书的格式按照教务处标准书写。
时间安排:指导教师签名: 年 月 日系主任(或责任教师)签名: 年 月 日用MATLAB 进行控制系统的动态性能的分析1 MATLAB 函数编程1.1 传递函数的整理已知三阶系统的闭环传递函数为:)64.08.0)(11(7.2)(2+++=s s s as G整理成一般式可以得到:G(s)=as a s a s a64.0)8.064.0()8.0(7.223+++++, 其中a 为未知参数。
从一般式可以看出系统没有零点,有三个极点(其中一个实数极点和一对共轭复数极点)。
1.2 动态性能指标的定义上升时间r t :当系统的阶跃响应第一次达到稳态值的时间。
上升时间是系统 响应速度的一种度量。
上升时间越短,响应速度越快。
峰值时间p t :系统阶跃响应达到最大值的时间。
最大值一般都发生在阶跃响应的第一个峰值时间,所以又称为峰值时间。
调节时间s t :当系统的阶跃响应衰减到给定的误差带内,并且以后不再超出给定的误差带的时间。
超调量 σp %:阶跃响应的最大值m ax c 超过稳态值)(∞c 的百分数σp %=)()(m ax ∞∞-c c c ×100%或者不以百分数表示,则记为σp =)()(m ax ∞∞-c c c超调量σp %反映了系统输出量在调节过程中与稳态值的最大偏差,是衡量系统性能的一个重要的指标。
自动控制理论实验报告实验二控制系统的时域分析一、实验目的学习利用MATLAB 进行控制系统时域分析,包括典型响应、判断系统稳定性和分析系统的动态特性;二、实验要点1、系统的典型响应有哪些?2、如何判断系统稳定性?3、系统的动态性能指标有哪些?三、实验方法(一)四种典型响应1、阶跃响应:阶跃响应常用格式:1、)(sys step ;其中sys 可以为连续系统,也可为离散系统。
2、),(Tn sys step ;表示时间范围0---Tn 。
3、),(T sys step ;表示时间范围向量T 指定。
4、),(T sys step Y =;可详细了解某段时间的输入、输出情况。
2、脉冲响应:脉冲函数在数学上的精确定义:0,0)(1)(0==?∞t x f dx x f 其拉氏变换为:)()()()(1)(s G s f s G s Y s f === 所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式:① )(sys impulse ;② );,();,(T sys impulse Tn sys impulse ③ ),(T sys impulse Y =(二)分析系统稳定性有以下三种方法:1、利用pzmap 绘制连续系统的零极点图;2、利用tf2zp 求出系统零极点;3、利用roots 求分母多项式的根来确定系统的极点(三)系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容实验三控制系统的根轨迹分析一实验目的1.利用计算机完成控制系统的根轨迹作图2.了解控制系统根轨迹图的一般规律3.利用根轨迹图进行系统分析二实验要点1. 预习什么是系统根轨迹?2. 闭环系统根轨迹绘制规则。
三实验方法(一)方法:当系统中的开环增益k 从0到变化时,闭环特征方程的根在复平面上的一组曲线为根轨迹。
基于MATLAB的二阶系统分析二阶系统指的是具有二阶传递函数的动态系统,通常表示为:G(s) = (ωn^2)/(s^2 + 2ζωns + ωn^2)其中,ωn表示自然频率,ζ表示阻尼比。
在MATLAB中,我们可以利用系统分析工具箱(Control System Toolbox)来对二阶系统进行分析。
以下将详细介绍如何使用MATLAB进行二阶系统的分析。
1.定义系统传递函数首先,我们需要定义一个二阶系统的传递函数。
在MATLAB中,传递函数可以使用tf函数来定义。
例如,下面是一个ωn=1,ζ=0.5的二阶系统的传递函数定义:sys = tf([1], [1 1 1]);2.绘制系统的零极点图利用pzmap函数可以绘制系统的零极点图,可以通过该图来观察系统的稳定性和动态特性。
例如,通过以下代码可以绘制上述系统的零极点图:figure;pzmap(sys);grid on;3.绘制系统的阶跃响应利用step函数可以绘制系统的阶跃响应,以观察系统的响应时间、超调量和稳态误差等性能指标。
例如,通过以下代码可以绘制上述系统的阶跃响应:figure;step(sys);grid on;4.绘制系统的频率响应利用bode函数可以绘制系统的频率响应曲线,以观察系统在不同频率下的增益和相位特性。
例如,通过以下代码可以绘制上述系统的频率响应曲线:figure;bode(sys);grid on;5.计算系统的稳态误差利用stepinfo函数可以计算系统的稳态误差和性能指标,例如超调量和响应时间等。
例如,通过以下代码可以计算上述系统的稳态误差:info = stepinfo(sys);steady_state_error = 1 - info.Peak;以上介绍了MATLAB中如何进行二阶系统的分析。
通过这些分析工具和函数,我们可以方便地对二阶系统的动态特性、频率响应和稳态性能等进行研究和评估,从而更好地设计和控制二阶系统。