5求图示桁架指定杆的内力
- 格式:doc
- 大小:42.50 KB
- 文档页数:2

学号 姓名11-5 力F 沿正六面体的对顶线AB 作用,F =100N ,求F 在ON 上的投影。
解:2220.330N 0.410.30.40.4x F F =-=-++ 2220.440N 0.410.30.40.4y F F ==++ 2220.440N 0.410.30.40.4z F F ==++ ON 方向单位矢量0.40.20.20.2ON j k =+ 400.4400.2N+N 83.8N 0.410.20.410.2ON F F ON =⋅==1-8 试求附图所示的力F对A点的矩,已知 1r =0.2m,2r =0.5m,F =300N 。
解:力F 作用点B o o121(sin 60,cos 60)r r r -o cos 60x F F =,o sin60y F F =o o 121()sin60(cos60)15kN m A y x M F r F r r F =⋅--⋅=-⋅1-9 试求附图所示绳子张力F T 对A 点及对B 点的矩。
已知F T =10kN ,l =2m ,R =0.5m,α=30°。
解:()100.55kN m A T T M F F R =⋅=⨯=⋅o o ()(sin 60)10(2sin 600.5) 5103=-12.3kN mB T T M F F l R =-⋅-=-⨯-=-⋅1-11 钢缆AB 的张力 F T =10kN 。
写出该张力F T 对x 、y 、z 轴的矩及该力对O 点的矩(大小和方向)。
解:(1)kN 36.2231104111222=⋅=++⋅=T Tx F FkN 36.2231104111222-=⋅-=++⋅-=T Ty F FkN 43.9234104114222-=⋅-=++⋅-=T Tz F F(2)对轴的矩(位置矢量k j r OA42+==)m kN 43.9234042)(⋅-=-=⋅-⋅=Ty Tz T x F F F MB2m kN 43.923404)(⋅==⋅=Tx T y F F M ,20()2 4.72kN m 32z T Tx M F F =-⋅=-=-⋅ (3)对点的矩()9.439.43 4.72(kN m)O T T x y z M F r F i j k M i M j M k =⨯=-+-=++⋅1-13 工人启闭闸门时,为了省力,常常用一根杆子插入手轮中,并在杆的一端C 施力,以转动手轮。
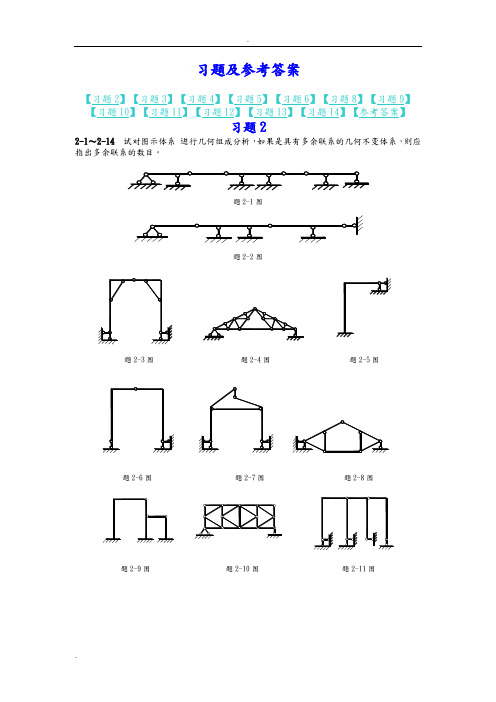
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。


6-1 题6-1图所示平面桁架,各杆Ef 相同,求在载荷P 作用下桁架各杆的内力。
解:(1)解除约束:系统静不定度为K=1,故解除1-2杆的约束, 代之以约束力X 1,如图6-1a 所示。
(2)内力分析:求<<P>>状态下的内力N p 、 单位状态<<1>> 下的内力N 1,内力分别如图6-1b,6-1c 所示。
(3)求典型方程中的影响系数δ11和载荷系数△1PEfdEf l N i i )223(2111+===∑ δ EfPdEf l N N i i P P 2111-===∆∑(4)求解多余约束力X 1:由典型方程01111=∆+P X δ解得:PP d EfEf Pd X P 172.0)223()223(22/1111≈-=+=∆-=δ(5)用叠加原理11X N N N P +=求出各杆的内力PN N P N N P N N P N )12(;)222(;)22(;)223(45342414251312-==-==-==-=6-2 题6-2图所示平面桁架,杆长AD=DC=BC=1m,AC 杆和BD 杆的截面积A AC =A BD =200mm 2,A AD =A DC =A BC =150mm 2, 各杆材料均相同,E =200KN/mm 2,当C 点受垂直载荷P =100KN 作用时,求该结构各杆的内力。
解:(1)解除约束:系统静不定度为K=1,故解除CD 杆的约束, 代之以约束力X 1,如图6-2a 所示。
(2)内力分析:求<<P>>状态下的内力N p 、 单位状态<<1>>下的内力N 1,内力分别如图6-2b,6-2c 所示。
(3)求典型方程中的影响系数δ11和载荷系数△1P1150.0803342111≈+===∑ i i Ef l N δ4316.048093411-≈-===∆∑P Ef l N N i i P P (4)求解多余约束力X 1:由典型方程01111=∆+P X δ解得:755.3663437233480480934/1111≈--=+⨯--=∆-=P P X P δ(5)用叠加原理求出各杆的内力: 11X N N N P +=KN N C B 480.88=-KN N D B 252.3-=-748.46=-C A NKN N D A 877.1=-KN N D C 755.3=-如图6-2d 所示。

土木工程力学(本)形成性考核册作业一一、选择题(每小题2分,共20分)1.三刚片组成几何不变体系的规则是(B)A 三链杆相联,不平行也不相交于一点B 三铰两两相联,三铰不在一直线上C 三铰三链杆相联,杆不通过铰D 一铰一链杆相联,杆不过铰2.在无多余约束的几何不变体系上增加二元体后构成(C)A 可变体系B 瞬变体系C 无多余约束的几何不变体系D 有多余约束的几何不变体系3.瞬变体系在一般荷载作用下,(C)A产生很小的内力 B不产生内力C产生很大的内力 D不存在静力解答4.已知某体系的计算自由度W=-3,则体系的( D )A自由度为3 B自由度等于0C 多余约束数等于3D 多余约束数大于等于35.不能作为建筑结构使用的是(D)A无多余约束的几何不变体系B有多余约束的几何不变体系C 几何不变体系 D几何可变体系7.下图所示结构的弯矩图形状应为(A)A 折线B 圆弧C 双曲线D 抛物线二、判断题(每小题2分,共20分)1.多余约束是体系中不需要的约束。
(⨯)2.如果体系的计算自由度大于零,那么体系一定是几何可变体系。
(∨)3.两根链杆的约束作用相当于一个单铰。
(⨯)4.一个体系是有n个自由度的几何可变体系,那么加入n个约束后就成为无多余约束的几何不变体系。
(⨯)题2-7图原结构是一个无多余约束的几何不变体系。
2.解:由二元体分析法原结构是一个无多余约束的几何不变体系。
3.解:显然,体系是具有两个多余约束的几何不变体系。
4.解:由三刚片规则,可知体系是无多余约束的几何不变体系。
四、绘制下图所示各结构的弯矩图。
(每小题10分,共30分)⨯ ⨯1.作弯矩图如下:2.解: 作弯矩图如下:3.D M解: 作弯矩图如下:五、计算图示桁架中指定杆件的内力。
解:求支座反力 由AM=0∑B P P F 4a F 2a F 3a 0--= PB 5F F ()4=↑ 由yF=0∑A P P P 5F F F F 04+--= P A 3FF ()4=↑用Ⅰ-Ⅰ截面将桁架截开,保留右边部分,受力如图: 由yF=0∑N1P P 5F sin 45F F4︒+-=N1P F F 4=-(压) 由CM=0∑M 图(kN •m )F F F P F 4ⅠP N3N15F a F a F cos 45a 04--︒= N3P 3F F 2=(拉)取结点C 为研究对象,作受力图如下: 显然:N2P F F =-(压)作业二一、选择题(每小题2分,共10分)1.用力法计算超静定结构时,其基本未知量为(D )A 杆端弯矩B 结点角位移C 结点线位移D 多余未知力2.力法方程中的系数ij δ代表基本体系在1=j X 作用下产生的(C )A i XB j XC i X 方向的位移D j X 方向的位移 3.在力法方程的系数和自由项中( B )A ij δ恒大于零B ii δ恒大于零C ji δ恒大于零D iP ∆恒大于零4.下列哪一条不是图乘法求位移的适用条件?( D ) A 直杆 B EI 为常数C P M 、M 至少有一个为直线形D P M 、M 都必须是直线形 5.下图所示同一结构在两种不同荷载作用下,它们之间的关系是(D ) A A 点的水平位移相同 B C 点的水平位移相同 C C 点的水平位移相同 D BC 杆变形相同F F N4二.判断题(每小题2分,共10分)1.静定结构由于支座移动引起的位移与刚度无关。
结构力学 第五章习题 参考答案2005级 TANG Gui-he (整理)5-1 试用结点法计算图示桁架各杆的内力。
5-2 试用结点法计算图示桁架各杆的内力。
解:由整体平衡条件可解得支座反力 F A =1.5F F B =1.5F 取结点A 为隔离体,如图,用数解法可解得 F A C =-2.12F F A B =1.5F 同理,依次取结点B 、C 、 D 、E 为隔离体,并由对称性可得各杆的内力如图。
4 * 8m60k N60k N6M 2MA B C D E FG H 解:由 M H =0 可得支座F a y=75kN.由 F Y=0 得 F h y=45kN 取 A 结点为隔离体,利用数解法可得 F N AB=-100kN. F NAC=125kN. 再取 C 点为隔离体,利用投影法和力平衡 可得 F N BC=-50,F NCE=103.1kN.同理依次取 B , D , E , G , F 可得各杆内力(如图所标)AC-60k N -90k N -100k N 45k N75k N125k N 75k N 42.4k N61.8k N 103.1k N -60k N -50k N -30k N55-4试判断图示桁架中的零杆。
解:图中红色的杆件为零杆在杆中标有 为零杆其中用到K 型和T 型结构判断原理5-5试用截面法计算图示桁架中指定杆件的内力。
2解:(1)求出支座竖向反力为2.5F (↑),(2)作截面I -I ,由∑M A=0得: 2.5F ×15-10F -5F +6F N 1=0 → F N 1=-3.75F (3)由∑M B=0得: 2.5F ×10-F ×5-F N 2×6=0 → F N 2=3.33F (4)利用勾股定理求出A B 杆长7.8F N 4x =5F N 4/3.84 由∑M C=0得: 2.5F ×10-5F +F N 1×6+6×5F N 4/7.8=0 → F N 4=0.65F (5)取结点B 为分析对象,由∑F Y=0得: F N 4×6/7.8+F N 3=0 → F N 3=-0.5F5-6试用截面法计算图示桁架中指定杆件的内力。
工程力学(理、材)_复习题(总16页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2《工程力学》本科复习题一、 单项选择题:解题要求:根据工程力学的基本概念和理论,从每小题的四个备选答案中选出一个正确的答案,并将正确答案的字母填写在相应的括号内。
1.若( B )中各分力对任意点之矩的矢量和为零,则该力系一定为平衡力系。
(A )汇交力系; (B )力偶系; (C ) 平面一般力系; (D )空间一般力系。
2. 应力是指( B )。
(A )受力物体截面上内力的分力, (B )受力物体截面上内力的分布集度, (C )受力物体截面上每一点的内力, (D )受力物体内部对外力的响应力。
(A )比例极限P σ; (B )弹性极限e σ; (C )屈服极限s σ; (D )强度极限b σ。
3. 用公式[]nuσσ=确定材料的许用应力值时,通常脆性材料是以其( D )作为极限应力(式中的u σ)。
(A )比例极限P σ; (B )弹性极限e σ; (C )屈服极限s σ; (D )强度极限b σ。
4. 杆件内力矢量沿其轴线的分量,称为( A )。
(A )轴力, (B )剪力, (C )扭矩, (D )弯矩。
5.关于扭弯组合:①公式WT M 22+≤[]σ是用( ①C )强度理论,为扭弯组合下的圆轴所建立的强度条件计算式。
② 公式WT M 2275.0+≤[]σ是用( D )强度理论,为扭弯组合下的圆轴所建立的强度条件计算式。
(A )第一 ; (B )第二; (C )第三; (D )第四6. 题图所示四个力系中,各力大小均为F ,分别以不同方式作用在边长为a 的正方形的四个顶点,其中一个力系的最简结果是一个力偶之矩M =Fa 且逆时针转动的合力偶,该力系是( D )。
(A )(B )(C )(D )一、6题 图7. 如图(a )所示,重为G 的均质圆柱在夹板AB 与墙壁AC 之间,夹板A 端有固定铰链支座与墙壁连接,B 端用绳索CB 拉住,CB 垂直于墙壁,若不计夹板AB 的自重和各接触处的摩擦。