桁架内力计算的截面法
- 格式:pdf
- 大小:471.87 KB
- 文档页数:43

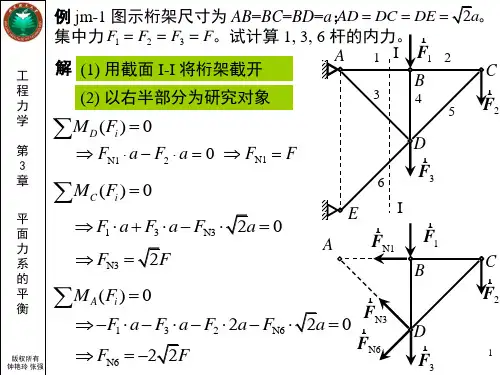

图1 屋架节点荷载的计算桁架的内力计算当桁架只受节点荷载时,其杆件内力一般按节点荷载作用下的铰接桁架计算。
这样,所有杆件都是轴心受压或轴心受拉杆件,不承受弯矩。
具体计算可用数解法(节点法或截面法)、图解法(主要是节点法)、图解法(主要是节点法)、计算机法(常用有限元位移法)等。
实际桁架节点为焊缝、铆钉或螺栓连接,具有很大的刚性,接近于刚接。
按刚接节点分析桁架时,各杆件将既受力又受弯矩。
但是,通常钢桁架中各杆件截面的高度都较小,仅为其长度的1/15(腹杆)和1/10(弦杆)以下,抗弯刚度较小;因而按刚接桁架算得的杆件弯矩M 常较小,且杆件轴心力N 也与桁架计算结果相差很小。
故一般情况都按铰接桁架计算。
对少数荷载较大的重型桁架,例如铁路桥梁等,当杆件截面高度超过其长度的1/10时,次应力份额逐渐增大,可达10~30%或以上,必要时应作计算。
目前用计算机计算刚接桁架已无困难。
据上所述,檩条或大型屋面板等集中荷载只作用在屋架节点处时,可按铰接桁架承受节点荷载计算杆件内力,例如图1。
这时节点荷载值即为檩条或边肋处的集中荷载值,按式上一小节公式,即:100011122F qA qbd d F qA qb d d d F qA qb == ==++== 来计算。
该图中檐口檩条集中荷载F 0在桁架计算时可归并入F 1内(或端节间按伸臂梁而将F 0(1+d 1/ d )并入F 1,-F 0 d 1/d 并入第二节点F );另外在计算上弦杆的支座截面时,除考虑轴心压力外还考虑偏心弯矩M e =F 0 d 1。
当檩条或屋面板等布置未与屋架节点相配合,屋面板没有边肋而是全宽度支图2 承受节间荷载的屋架 承于屋架上弦(上弦均布荷载)、或其它特殊情况时,桁架将受节间荷载,例如图1。
这时桁架内力计算可按下列近似方法:(1)把所有节间内荷载按该段节间为简支的支座反力关系分配到相邻两个节点上作为节点荷载,据此按铰接桁架计算杆件的轴心力。



结构力学桁架截面法例题
结构力学桁架截面法例题
一、题目:
一根钢桁架有两种不同截面,桁架长度为3m,端部修里夹具为α=60°,桁架的两个截面信息如下:
截面1:
a1=20mm,b1=10mm,I1=40×104mm4
截面2:
a2=50mm,b2=20mm,I2=500×104mm4
请用桁架截面法计算其承载力。
二、解答:
1、计算桁架的顶点角度θ和抗弯矩Mx:
利用转矩定理,可以得到桁架承载力P的表达式:
P=Mx/l*cosθ
用已知量计算得θ=30°,Mx=12.33×104N·m
2、求解桁架的承载力P:
将计算得的θ和Mx代入表达式:
P=12.33×104N·m/3m*cos30° = 4.11×104N
3、计算桁架的屈曲应力σbb:
利用屈曲应力的表达式:
σbb=Mx/S
用已知量计算得S=12.5×104mm2,σbb=0.99MPa。
以上便是本题的答案。
桁架承载力P=4.11×104N,屈曲应力σbb=0.99MPa。

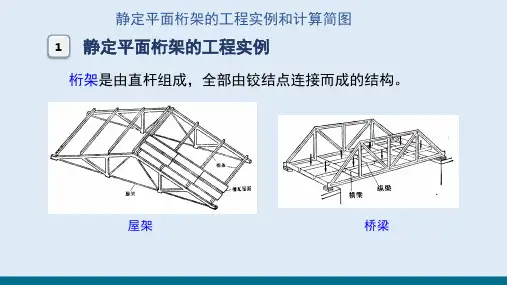
25您的位置:在线学习—>在线教程—>教学内容上一页返回目录下一页3.4 静定平面桁架教学要求掌握静定平面桁架结构的受力特点和结构特点,熟练掌握桁架结构的内力计算方法——结点法、截面法、联合法3.4.1 桁架的特点和组成3.4.1.1 静定平面桁架桁架结构是指若干直杆在两端铰接组成的静定结构。
这种结构形式在桥梁和房屋建筑中应用较为广泛,如南京长江大桥、钢木屋架等。
实际的桁架结构形式和各杆件之间的联结以及所用的材料是多种多样的,实际受力情况复杂,要对它们进行精确的分析是困难的。
但根据对桁架的实际工作情况和对桁架进行结构实验的结果表明,由于大多数的常用桁架是由比较细长的杆件所组成,而且承受的荷载大多数都是通过其它杆件传到结点上,这就使得桁架结点的刚性对杆件内力的影响可以大大的减小,接近于铰的作用,结构中所有的杆件在荷载作用下,主要承受轴向力,而弯矩和剪力很小,可以忽略不计。
因此,为了简化计算,在取桁架的计算简图时,作如下三个方面的假定:(1)桁架的结点都是光滑的铰结点。
(2)各杆的轴线都是直线并通过铰的中心。
(3)荷载和支座反力都作用在铰结点上。
通常把符合上述假定条件的桁架称为理想桁架。
3.4.1.2 桁架的受力特点桁架的杆件只在两端受力。
因此,桁架中的所有杆件均为二力杆。
在杆的截面上只有轴力。
3.4.1.3 桁架的分类(1)简单桁架:由基础或一个基本铰接三角形开始,逐次增加二元体所组成的几何不变体。
(图3-14a)(2)联合桁架:由几个简单桁架联合组成的几何不变的铰接体系。
(图3-14b)(3)复杂桁架:不属于前两类的桁架。
(图3-14c)3.4.2 桁架内力计算的方法桁架结构的内力计算方法主要为:结点法、截面法、联合法结点法――适用于计算简单桁架。
截面法――适用于计算联合桁架、简单桁架中少数杆件的计算。
联合法――在解决一些复杂的桁架时,单独应用结点法或截面法往往不能够求解结构的内力,这时需要将这两种方法进行联合应用,从而进行解题。
25您的位置:在线学习—>在线教程—>教学内容上一页返回目录下一页3.4 静定平面桁架教学要求掌握静定平面桁架结构的受力特点和结构特点,熟练掌握桁架结构的内力计算方法——结点法、截面法、联合法3.4.1 桁架的特点和组成3.4.1.1 静定平面桁架桁架结构是指若干直杆在两端铰接组成的静定结构。
这种结构形式在桥梁和房屋建筑中应用较为广泛,如南京长江大桥、钢木屋架等。
实际的桁架结构形式和各杆件之间的联结以及所用的材料是多种多样的,实际受力情况复杂,要对它们进行精确的分析是困难的。
但根据对桁架的实际工作情况和对桁架进行结构实验的结果表明,由于大多数的常用桁架是由比较细长的杆件所组成,而且承受的荷载大多数都是通过其它杆件传到结点上,这就使得桁架结点的刚性对杆件内力的影响可以大大的减小,接近于铰的作用,结构中所有的杆件在荷载作用下,主要承受轴向力,而弯矩和剪力很小,可以忽略不计。
因此,为了简化计算,在取桁架的计算简图时,作如下三个方面的假定:(1)桁架的结点都是光滑的铰结点。
(2)各杆的轴线都是直线并通过铰的中心。
(3)荷载和支座反力都作用在铰结点上。
通常把符合上述假定条件的桁架称为理想桁架。
3.4.1.2 桁架的受力特点桁架的杆件只在两端受力。
因此,桁架中的所有杆件均为二力杆。
在杆的截面上只有轴力。
3.4.1.3 桁架的分类(1)简单桁架:由基础或一个基本铰接三角形开始,逐次增加二元体所组成的几何不变体。
(图3-14a)(2)联合桁架:由几个简单桁架联合组成的几何不变的铰接体系。
(图3-14b))3-14c复杂桁架:不属于前两类的桁架。
(图)3(.3.4.2 桁架内力计算的方法桁架结构的内力计算方法主要为:结点法、截面法、联合法结点法――适用于计算简单桁架。
截面法――适用于计算联合桁架、简单桁架中少数杆件的计算。
联合法――在解决一些复杂的桁架时,单独应用结点法或截面法往往不能够求解结构的内力,这时需要将这两种方法进行联合应用,从而进行解题。
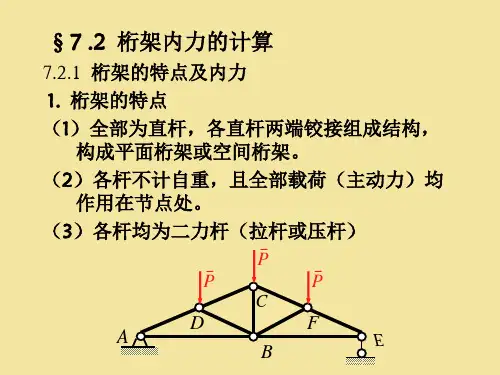
平面简单桁架的内力计算平面简单桁架节点1、各杆件为直杆, 各杆轴线位于同一平面内;2、杆件与杆件间均用光滑铰链连接;3、载荷作用在节点上,且位于桁架几何平面内; 4、各杆件自重不计或均分布在节点上在上述假设下, 桁架中每根杆件均为二力杆,称为理想桁架。
关于平面桁架的几点假设:有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)求解桁架内力的方法1、节点法2、截面法桁架的每个节点都受一个平面汇交力系作用。
为了求每一个杆件的内力,可以逐个地取节点为研究对象,由已知力求出全部未知的杆件内力的方法。
例题 已知: P =10kN,尺寸如图;求: 桁架各杆件受力. 解: 取整体,画受力图.取节点A ,画受力图. ∑=0x F ∑=0y F ∑=0B M 0=Bx F 042=−Ay F P kN5=Ay F 0=−+P F F By Ay kN 5=ByF ∑=0y F030sin 01=+F F Ay kN 101−=F (压)∑=0x F 030cos 012=+F F kN 66.82=F (拉)取节点C ,画受力图. ∑=0x F 030cos 30cos 0'104=−F F kN 104−=F (压)∑=0y F ()030sin 04'13=+−−F F F kN 103=F (拉)取节点D ,画受力图.∑=0x F 0'25=−F F kN 66.85=F (拉) 有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)取节点C ,画受力图. ∑=0x F 030cos 30cos 0'104=−F F kN 104−=F (压)∑=0y F ()030sin 04'13=+−−F F F kN 103=F (拉)取节点D ,画受力图.∑=0x F 0'25=−F F kN 66.85=F (拉)有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)。
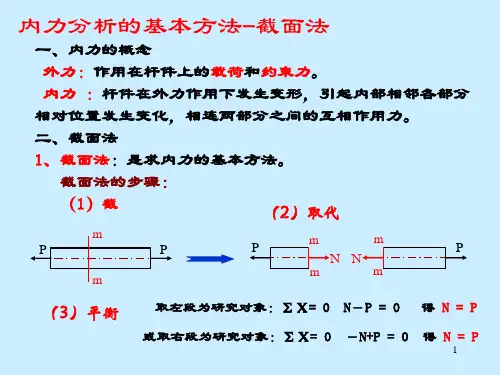
截面法截面法可以快速求出某一内力,通常取结构 的一部分为隔离体,其上力系为平面一般力 系。
每个隔离体上有3个独立平衡方程。
一般 表示为: ∑FX = 0 投影法 ∑FY = 0 力矩法 ∑M = 0 计算要点: 尽量使一个方程解一个未知数,避免求解 联立方程。
1一. 力矩法例:求图示桁架1、2、3杆的轴力。
2VAVB解:由整体平衡条件求得支座反力 VA=VB HA=0作Ⅰ--Ⅰ截面,截开1、2、3杆的轴力 取截面以左为隔离体。
Ⅰ3Ⅰ(1)求1杆轴力N1K14选取未知力N2和N3 延长线的交点K1作 为取矩点。
N1 对K1点取矩,由 ∑MK1 = 0 从而求出所求未知 力N1。
VA(2)求2杆轴力N2N2Y25K2X22VA由∑MK2 = 0 ,比例关系从而求出所求未知力Y2。
2杆轴力N2(3)求3杆轴力N3Y3 N3 X3K3 VA6由 ∑MK3 = 0比例关系从而求出所求未知力X3。
3杆轴力N3力矩法要点:欲求某指定杆内力,则作一截面,截开待求 杆; 隔离体上除所求未知力外,其余未知力的延 长线均交于某一点K。
对K点取矩,从而求出所求未知力 。
(1)选择其余未知力延长线的交点K作为取矩 点,从而用∑MK=0,求出指定杆内力。
(2)将斜杆的内力放在某一个合适的点上分 解,使其一个分力通过取矩点K。
解,7例1. 求图示桁架杆件a、b、c的轴力890kN30kN作Ⅰ—Ⅰ截面Ⅰ9Ⅰ求NaNa 求Na时,对另 外两个未知力的 交点C取矩, C10由 ΣMc=0,得 Na×4+30×8=030kN解得: Na =- 60kN求NbD Xb E Yb Nb30kN11求Nb时,对点D取 矩。
将Nb 其在E点处分解 为水平和竖向分量。
由ΣMD=0,得 Yb×12+40×4 - 30×12=0 解得 Yb=16.67 kN由比例关系得到:N b = 2Yb = 2 × 16.67 = 23.57kN求NcYc XcD Nc12E求Nc时,对点E取 矩。
将Nc 其在D点处分解 为水平和竖向分量。
由ΣME=0,得 Yc×12 - 40×8 =0 解得 Yc= 26.67kN30kN由比例关系得到:N c = 2Yc = 2 × 26.67 = 37.71kN二. 投影法例:求图示桁架a杆的轴力.P P13mmNa作m-m截面,截开a 杆,取截面以上为隔离 体。
其上共有四个未知力。
投影法P14当隔离体上除所求 未知力Na外,其余未知 力均相互平行且都在竖 直方向上。
将Na 分解为水平和竖 向分量Xa 、Ya。
建立水平投影方程 ∑FX=0,可求出 Xa=- P 由比例关系得到 Na 。
Xa Ya Na投影法要点:欲求某指定杆内力,则作一截面,截开待求 杆; 当隔离体上除待求未知力外,其余未知力均相 互平行。
建立投影方程,求出待求未知力。
15例2. 试求图示桁架a、b杆的内力Ⅰ Ⅰ2l163l作Ⅰ-Ⅰ截面,截开a 杆,取截面以上为隔 离体。
其上共有三个未知力。
a杆的内力17Xa建立水平投影方程 ∑FX=0,可求出 由比例关系得到Xa = PNa = 2Pb杆的内力18ⅡⅡ作Ⅱ-Ⅱ截面,截开b杆,取截面以上为隔 离体。
其上共有五个未知力。
b杆的内力19Xb建立水平投影方程 ∑FX=0,可求出 由比例关系得到Xb=2P Nb = 2 2P联合桁架先求出联系杆件的内力,即先求出刚片间的约束 力,然后将约束力作为已知的荷载加在刚片上(简 单桁架上)。
20CSS∑MC = 0S∑Y = 0S=0例3 试求图示桁架杆a、b的内力。
213lVA=PVB=P联合桁架3l求1杆的内力Ⅰ221建立竖直投影方程 ∑Fy=0,可求出 y1 = 0N1 = 0VA=P Ⅰ VB=P求a杆内力作Ⅱ-Ⅱ截面,截开 b杆,取出隔离体.0 0Na Xa Ya O23P 对0点取矩,有∑M0= 0,即: Ya = − 3 1 Na = − 2P 3ⅡⅡ求b杆内力作Ⅱ-Ⅱ截面,截开 b杆,取出隔离体.0 0Nb24ⅡⅡA YbXb2 对A点取矩,有∑MA=0,即:Yb = − P 3 1 Nb = − 5P 3试求图示桁架杆a、b的轴力25联合桁架求a杆的轴力26联合桁架切断联合杆AC、EF及BD∑x = 0Na=P求b杆的轴力27∑MA=0Xb例4 试求图示桁架指定杆的内力。
287 P 28d7 P 22求5杆内力Ⅰ 5297 P 2Ⅰ7 P 2作Ⅰ-Ⅰ截面,截开5杆,取截面以左(或以右) 为隔离体。
求1杆内力N530C7 P 2对C点取矩,有∑MC=0,即: 7 × 4 − 3 − 2 −1 N 5 = N1 = − 2 P = −4 P 2求3杆内力5317 P 2ⅡⅡ7 P 2作Ⅱ-Ⅱ截面,截开3杆,取出隔离体。
求3杆内力N3 X3 Y3 C32对C点取矩,有∑MC= 0,即:1 Y3 = − P 2 1 N3 = − 2P 2求2杆内力Ⅲ3357 P 2Ⅲ7 P 2作Ⅲ-Ⅲ截面,截开2杆,取截面以左(或以右) 为隔离体。
求2杆内力Y21 P 234建立竖直投影方程 ∑Fy= 0,可求出Y2 = PN 2 = 2P7 P 2求4杆内力D35取D结点隔离体,由结点法分析。
建立竖直投影方程 ∑Fy= 0,可求出 N 4 = −PN4DP讨论:P78 例3-1636,b0 c0 0aIdI例3-16b、d杆内力∑Fx=0,得G37∑MG=0bc,aFNd = 0IId0FNd例3-16 a 杆内力38Fb0 caId0, 0I FNaFNa∑MF=010 × 2 + 10 × 4 =− = −30kN 2例D 1试求图示桁架a杆的内力D点为K式结点, 其上无外荷载,由 ∑Fy= 0,可求出: Y1=-Y2 由对称性,有: Y1=Y2 其解为: N1=N2 =039002DY1Y2作I-I截面,取右半为隔离体,对O点取矩。
I Na O40000I∑MO=06×Na-20×3=0Na=10kN例5. 求图示桁架1、2杆的轴力4115kN15kN解:先根据整体平衡条件求出桁架支座反力.求杆件1的轴力Ⅰ42N1ⅠM0 C10kN15kNC 对C点取矩,有∑MC=0,即: 15kN 15×4+N1×3-10×2=00 MC 10 × 2 − 15 × 4 N1 = =− h 3平弦桁架上下弦杆承 受梁中的弯矩。
N1=-13.3kN求杆件2的轴力Ⅰ43Y2ⅠD10kN15kNQ0 CDC15kN有∑Y =0, 15+Y2-10=0Y2 = 10 − 15 = −50 = −QCD平弦桁架的斜杆承受 梁中的剪力。
32 + 2 2 5 5=− N2 = − 13 kN 3 3。