沪科版七年级分式全章复习[1]

《分式》复习（1）
教学目标：通过例题分析，理解分式的相关概念及其基本性质，知道分式有意义和分式值为零的条件，掌握分式运算的法则；通过对分式的四则混合运算的复习过程，体会化归的数学思想，逐步形成自主、合作交流的意识和严谨的学习态度.
教学重点：理解分式的相关概念，会进行分式的四则运算.
教学难点：能准确、灵活地进行分式运算.
教学设计：
教学设计说明：
本节课是七年级数学第十章《分式》的一节复习课，七年级学生在学习了整式和因式分解后对代数式有了一定的认识，进一步学习分式，既是对整式的运用和巩固，也是对整式的延伸。

本节课主要围绕分式的相关概念及其运算展开复习，重点放在了分式的四则运算上，教学中主要针对以下几方面展开：
一、关注学生解决实际问题的能力
数学来源于生活，并服务于生活，本节课设置三个情境问题，既可以检测学生学习本章知识后解决问题的能力，也引出了分式中的相关概念和性质，帮助学生梳理这些知识点。

并将情境三这个问题继续穿插到分式的运算中。

二、关注学生的运算能力
分式的运算是中考的重点，故我把本课的教学重点放在了分式的运算上，通过对问题3和问题4的解决，归纳分式四则运算的法则，再让学生运用法则解决后面的计算问题，规范解题格式。

在点拨学生发现分式运算过程中，有时将分式中的多项式进行因式分解后计算会
更简单。

三、关注学生解题经验的积累
在分式的运算过程中，学生往往会有各种各样的错误呈现，而这些错误无疑是课堂上发现的宝贵财富，所以在教学中，我通过让学生相互交流解题方法、合作收集错误案例的方法，让学生积累解题的经验，争取能让错误不重复犯。

第九章 分 式一、知识总结（一）分式及其性质1、分式（1）定义：一般的，如果a ，b 表示两个整式，并且b 中含有字母，那么式子b a 叫做分式；其中a 叫做分式的分子，b 叫做分式的分母。

（2）有理式：整式和分式统称为有理式。

（3）分式=0⇔分子=0，且分母≠0 （分式有意义，则分母≠0）（4）最简分式：分子和分母没有公因式的分式。

2、分式的性质分式的分子与分母都乘以（或除以）同一个不等于零的整式，分式0m ≠的值不变 即：mb m a m b m a b ÷÷=⋅⋅=a （a ，b ，m 都是整式，且） 分式的性质是分式化简和运算的依据。

3、约分：把一个式子的分子分母的公因式约去叫做约分。

注：约分的结果应为最简分式或整式。

约分的方法：1）若分子、分母均为单项式：先找分子、分母系数的最大公约数， 再找相同字母最低次幂；2）若分子、分母有多项式：先把多项式因式分解，再找分子、分母的公因式。

（二）分式运算1、分式的乘除1）分式乘法法则：两分式相乘，用分子的积做分子，分母的积做分母；即：bdac d c b =⨯a 2）分式除法法则：两分式相除，将除式的分子、分母颠倒位置后，与被除式相乘； 即：bcad c d b a d c b =⨯=÷a 3）分式乘方法则：分式的乘方就是分子分母分别乘方。

即：n n n b a b =⎪⎭⎫ ⎝⎛a ，()n n ab b 1a -=⎪⎭⎫ ⎝⎛2、分式的加减 1）同分母分式加减：分母不变分子相加减；即：bc a b c b ±=±a ()0b ≠ 2）异分母分式加减：先通分，变为同分母的分式相加减， 即：bdbc ad bd bc bd ad d c b ±=±=±a ()0b ≠d （三）分式方程1、定义：分母中含有未知数的方程叫做分式方程。

2、解法： 1）基本思路：分式方程−−→−转化整式方程 2）转化方法：方程两边都乘以各个分式最简公分母，约去分母。

分式方程章节复习课前测试【题目】课前测试A、B两地相距50千米，甲骑自行车，乙骑摩托车，都从A地到B地，甲先出发1小时30分，乙的速度是甲的2.5倍，结果乙先到1小时，求甲、乙两人的速度。

【答案】甲速度为12千米/时，乙速度为30千米/时【解析】解：设甲速为x千米/时，则乙速为2.5千米/时，依题意，有：解得：经检验是原方程的根，且符合题意当时，总结：本题考察了分式方程的实际应用以及列分式方程．【难度】3【题目】课前测试当x ＝ 时，分式5x x -与另一个分式62x x --的倒数相等【答案】10【解析】由题意可知5x x -=62--x x ∴)2)(5()6(--=-x x x x得107622+-=-x x x x解得x=10检验：当x=10时，原式成立总结：本题主要考查了解分式方程，但注意题目的要求【难度系数】3知识定位适用范围：沪教版，七年级知识点概述：本章重点部分是可化为一元一次方程的分式方程。

其中可化为一元一次方程的分式方程分为分式方程的定义、分式方程的解、解分式方程、换元法解分式方程，分式方程的增根，主要进行分式方程的复习。

适用对象：成绩中等偏下的学生注意事项：基础差的学生着重掌握分式的加减，分式的乘除，可化为一元一次方程的分式方程，中等偏上的学生重点掌握可化为一元一次方程的一些难题和好题目进行综合练习。

重点选讲：①分式方程的概念②可化为一元一次方程的分式方程③分式方程的应用知识梳理知识梳理1：分式方程的概念知识梳理2：解分式方程分式方程：分母里含有未知数的方程叫分式方程。

如：81x -+，1613122-=-++x x x 是分式方程5132+=+x x ， 6x 2+4x +1=0是整式方程注：分母中是否含有未知数是分式方程与整式方程的根本区别，分母中含未知数就是分式方程，否则就为整式方程。

?步骤：例如，解方程x 180-x2180=2 1、两边都乘以最简公分母2x ，2、得到整式方程180=4x .3、解这个方程，得 x =454、x =90是不是原来分式方程的根呢？把x =45代入原方程检验。

沪科版七年级分式全章习题经典★★work Information Technology Company.2020YEAR分式第一节：分式的概念及性质 【典例分析】1.下列代数式中，哪些是整式哪些是分式x x x x y x b a a 2,11,81,4,22,3,4-+---π 2. x 为何值时，分式112--x x 的值为0.3.利用分式的基本性质填空：（1）22(____)y x y x y x -=+- （2）(___)32ba ab ab a -=- （3）(___)244422+=+--x x x x 4.求分式的值： （1）若,432zy x ==求222z y x zx yz xy ++++的值. （2）求2242y x yx -+的值，其中x=5,y=3.55.分式的应用一件工作，a 人b 天可以完成，c 人一天能做工作的几分之几？6.把下列的分式的分子、分母的系数化为整数.（1）y x yx 213121+- （2）y x y x 01.022.13.2+- 7.（1）已知分式41262-+-a a 的值为正整数，求式中的a 的值 （2）xx x --266的值为正整数，求整数x 的值 （3）242+-x x 的值是正整数，则整数x 的值为_____ （4）113++-x x 的值为整数，则整数x 的值是______（5）124+x x的值是整数，则x 整数的值为________8.若分式：96932+--a a a 的值为正时，a 的取值范围是________ 若分式：9632+-a a a的值为正，则a 的取值范围是________ 【经典练习】： 1.使分式133+-x 的为负数的条件是________ 2.如果分式yx yx +-中的x 和y 都扩大为原来的4倍，那么分式的值_____3.化简44422-+-x x x4.(1)当a________时，等式xxx a x a -=---1)1)(3()3(成立.(2)aaa a a a -=---1)1)(3()3(成立，则a 满足的条件为_______5.已知2=y x ，则分式222263y xy x y xy x +++-的值为_________若22224,2bab a b ab a b a a b ++++=+则的值是__________6.已知不论x 取什么数时，分式)05(,53≠+++bx bx ax 都是一个定值，求a 、b 应满足的关系式，并求出这个定值.7.在分式①a b b a --- ，②ab ba -+-，③b a b a ----，④a b b a -+-中与分式ba b a -+相等的是_______8.化简：（1）144222+--a a aa （2）mm mm m -+-3232第二节：分式的乘除法 【典例分析】1.利用分式的乘除法法则计算（1）4923375453512y x n m mn y x -⋅- （2）y xz y z x 324222-÷ 2.分式的乘方（1）432⎪⎪⎭⎫ ⎝⎛-b a （2）322⎪⎪⎭⎫⎝⎛-z y x3.分式的乘除混合运算（1）22223222bab a ba b a a b ab a a b a +-+⋅-÷++-（2）⎪⎪⎭⎫⎝⎛-÷-÷+--x y xy y x x y xy xy x 222222（3）xx x x x x x ---⋅+÷+-++34)3(44692224.化简求值：21,23,2)(2222==-⋅-+-÷-y x x y x y x y xy x x xy 其中5.已知0200452=--x x ，求代数式21)1()2(23-+---x x x【经典练习】： 1.使代数式4233-+÷-+x x x x 有意义的 x 的值为_________2.如果,32=b a 且2≠a ，那么51-++-b a b a =___________3.化简求值：22232232bab a b b b a ab a b a b +-÷-+⋅-，其中3,32-==b a4.一台电子收报机，它的译电效率相当于人工译电效率的75倍，试计算人工译电2000个字所用的时间是电子收报机译电3000个字所需的时间的多少倍？5．观察下列式子111111111,, (1222363412)=+=+=+归纳出的一般结论是 ___（用n 表示）。

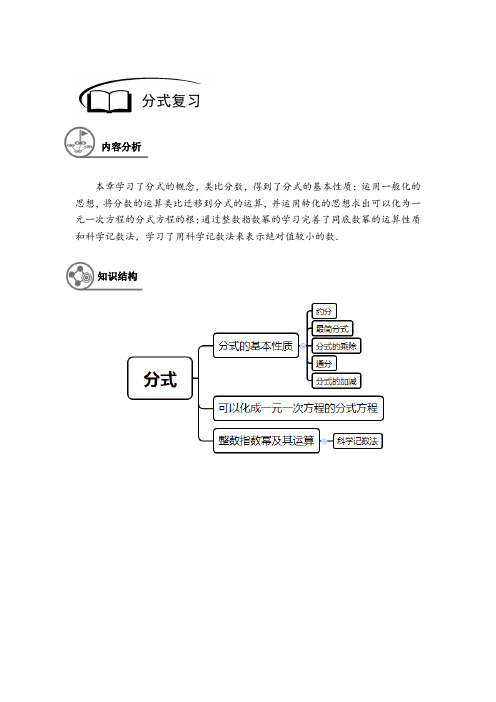
本章学习了分式的概念，类比分数，得到了分式的基本性质；运用一般化的思想，将分数的运算类比迁移到分式的运算，并运用转化的思想求出可以化为一元一次方程的分式方程的根；通过整数指数幂的学习完善了同底数幂的运算性质和科学记数法，学习了用科学记数法来表示绝对值较小的数．分式复习内容分析知识结构2 / 12【例1】下列判断中，正确的是（）．A ．分式的分子中一定含有分母B ．当0B =时，分式AB 无意义C ．当0A =时，分式AB的值为0（A B 、无意义）D ．分数一定是分式【例2】若分式36a ba b-+的值为零，则a 和b 的关系是_________．【例3】不改变分式的值，使分式115101139x yx y -+的各项系数化为整数，分子、分母应乘以（ ）． A ．10B ．9C ．45D ．90【例4】在分式()222221332212x a b x y a bx x a b a bx y -+-+++++，，，中，最简分式有__________个．【例5】（1）用科学记数法表示：0.00003082________=； （2）82.310--⨯=___________．【例6】已知b a x a b -=，b ay a b+=，则22_____x y -=．例题解析【例7】甲、乙两班学生植树造林，已知甲班每天比乙班多植5棵树，甲班植80棵树所用的 天数与乙班植70棵树所用的天数相等，如果设甲班每天指数x 棵，那么根据题意 列出的方程是（ ）．A ．80703x x =-B ．80705x x =+C ．80705x x =+ D ．80705x x =-【例8】已知分式1x yxy+-的值是m ，如果分式中x y 、用它们的相反数代入，那么所得的值为 n ，则m n 、的关系是什么？【例9】当x 满足_________条件时，分式1111x++有意义．【例10】学生有m 个，若每n 个人分配1间宿舍，则还有一人没有地方住，问宿舍的间数为 （ ）．A ．1m n + B ．1m n - C ．1m n- D ．1m n +【例11】如果分式225621x x x x --+-的值等于零，那么x 的值是（）．A ．6B ．1-C ．6-或1D ．1-或64 / 12【例12】将三个数067⎛⎫- ⎪⎝⎭，123-⎛⎫- ⎪⎝⎭，132-⎛⎫⎪⎝⎭按从小到大的顺序排列：______________________．【例13】若13m m +=，则221______m m +=；441_______m m+=．【例14】计算：（1）()2222x y x y x y y x +⋅+--；（2）211121a a a a ⎛⎫-÷ ⎪--+⎝⎭；（3）22222a b a b a ba b a b ab ⎛⎫+---⋅ ⎪-+⎝⎭．【例15】计算：3-3231783211387233--⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫÷+-÷--+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭．【例16】求下列各式中的x ．（1）25168x x +=；（2）3.6100.036x ⨯=．【例17】已知()()2641212x x A B Cx x x x x x +-=++-+-+，求A B C 、、的值．【例18】计算：2222x z y x y zx xy xz yz x xy xz yz+-++--+-+++．【例19】已知22x y xy -=，且0xy ≠，求2222x y x y --+的值．【例20】解方程：（1）22133xx x -=--； （2）2222211242x x xx x x x x+---=--+．【例21】当k 为何值时，解关于x 的方程2111x k xx x x -=--+时，不会产生增根．【例22】当2x >时，试比较分式21x x --和32x x --的值的大小．【例23】已知4x y +=-，12xy =-，求1111y x x y +++++的值．【例24】文化用品商店用2000元购进一批学生书包，面市后发现供不应求，商店又购进第二批同样的书包，所购数量是第一批购进数量的3倍，但单价贵了4元，结果第二批用了6300元．（1）求第一批购进书包的单价是多少元？（2）若商品销售这两批书包时，每个售价都是120元，全部售出后，商店共盈利多少元？【例25】解方程：48755986x x x xx x x x----+=+----．【例26】已知2520160x x--=，求()()322112x xx---+-的值．【例27】已知2112 xx x =-++，求2232111x xx x x-+-+-的值．【例28】如果111n m m n++=+，求22m nn m⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭．【例29】已知a b c、、为实数，且13aba b=+，14bcb c=+，15cac a=+，那么abcab bc ca++的值是多少？【例30】计算：111(1)(2)(1)(2)(3)(98)(99)(100)n n n n n n n n n++⋅⋅⋅+++++++++．6/ 12【习题1】下列各式：22212331331054x y x y xy x x y y x x y π+----+、、、、、、、，其中分式的个数是（ ）． A ．1B ．2C ．3D ．4【习题2】下列等式中，成立的是（）．A ．()()a bc d a b c d +=+++ B ．50.0150010.220y y y y++=C ．221x y x y x y-=-- D ．1a ba b ---=--【习题3】如果把223xyx y-中的x 与y 都扩大5倍，那么分式的值（ ）．A ．扩大5倍B ．不变C ．缩小5倍D ．无法确定【习题4】已知1纳米910-=米，某植物花粉的直径为3500纳米，那么用科学记数法表示该 种花粉的直径为________米．【习题5】汽车从甲地开往乙地，每小时行驶1v km ，t 小时可以到达，如果每小时多行驶2v km ，那么可以提前到达的小时数为（ ）．随堂检测8 / 12A ．212v tv v + B ．112v tv v + C ．1212v v v v + D ．1221v t v t v v -【习题6】已知234a b c==，则22222232a b c a ab c -+-+的值为（ ）． A ．32- B ．38-C ．12 D ．2【习题7】已知关于x 的方程3211x kx x --=-+有增根，则_______k =．【习题8】把333222111235---、、这三个数按从大到小的顺序排列是______________________．【习题9】已知1122xx x+=--，且2212x y xy +=，求x y 、的值．【习题10】A B 、两地相距36千米，一艘小船从A 地匀速顺流航行至B 地，又立即从B 地匀 速逆流返回A 地，共用去9小时．已知水流速度为3/km h ，若设该轮船在静水中的速 度为/xkm h ，则求x 时所列方程式______________________．【习题11】若2221120x a x b x x ⎛⎫++-++-= ⎪⎝⎭，则a b ，之间的关系式是________________．【习题12】若22103460a b a b +-+-=，求a ba b+-的值．【习题13】先化简，再求值：2234221121x x x x x x ++⎛⎫-÷ ⎪---+⎝⎭，其中x 是不等式组40251x x +>⎧⎨+<⎩的 整数解．【习题14】解方程：（1）232x xx x -=+-；（2）34522341x x x x x x x x +++++=+++++．【习题15】一项工程，甲队单独做完所需天数是乙、丙两队合做所需天数的a 倍，乙队独做 所需天数是甲、丙两队合做所需天数的b 倍，丙队独做所需天数是甲、乙两队合做所需天数的c 倍，求111111a b c +++++的值．【习题16】()()()()()()()()2222133********x x x x x x x x +++⋅⋅⋅+++++++++．10 / 12【习题17】如果关于x 的方程21221232a a x x x x ++=---+无解，求a 的值．【作业1】无论x 取什么数时，总有意义的分式是（ ）．A ．21x x -+B ．2(1)x x + C ．338xx + D ．25x x -【作业2】当______x 时，分式11x--的值为负数．【作业3】约分：22229_____________215a b a ab b -=--．【作业4】4x xy ，326y x，210x y y -的最简公分母是___________．【作业5】计算：21141_______35--⎛⎫⎛⎫-⨯-⨯-= ⎪ ⎪⎝⎭⎝⎭．课后作业【作业6】计算：（1）222222253214111a a a a a a a a --++-++++； （2）212293m m+--； （3）211x x x -++； （4）2211xy x y x y x y ⎛⎫÷- ⎪--+⎝⎭．【作业7】解方程：（1）2331y y y +=-； （2）23222x x x -=+-； （3）2227461x x x x x +=+--； （4）232133648x x -+-+-=．【作业8】已知22221111x x x y x x x x+++=÷-+--，试说明不论x 为何值，y 的值不变．【作业9】如果11t x t -=+，2332t y t-=-，那么用含x 的代数式表示y 得___________．【作业10】设1x y z a b c ++=，0a b c x y z ++=，求222222x y z a b c ++的值．12 / 12【作业11】计算：2422481111x x x x +++-+++．。

沪科版七年级数学下册第九章《分式》单元同步复习讲义 01 本章结构图分式⎩⎪⎨⎪⎧分式⎩⎪⎨⎪⎧概念、基本性质分式的化简分式的运算⎩⎪⎨⎪⎧分式的乘除分式的加减整数指数幂分式方程⎩⎪⎨⎪⎧分式方程的解法分式方程的应用 02 重难点突破重难点1 分式的有关概念及基本性质【例1】 (衡阳中考)若分式x －2x ＋1的值为0，则x 的值为(C ) A ．2或－1 B ．0C ．2D ．－1【方法归纳】 分式的值为0需要同时具备两个条件：分子等于0，分母不等于0，二者缺一不可．1．(成都中考)要使分式5x －1有意义，则x 的取值范围是(A ) A ．x ≠1 B ．x ＞1C ．x ＜1D ．x ≠－12．下列等式成立的是(C )A .1a ＋2b ＝3a ＋bB .12a ＋b ＝1a ＋bC .ab ab －b 2＝a a －bD .a －a ＋b ＝－a a ＋b3．(赤峰中考)化简a 2b －ab 2b －a结果正确的是(B ) A ．ab B ．－abC ．a 2－b 2D ．b 2－a 2重难点2 分式的运算【例2】 (雅安中考)先化简，再求值：(1－1m )÷m 2－1m 2＋2m ＋1，其中m ＝2. 解：原式＝(m m －1m )÷（m ＋1）（m －1）（m ＋1）2＝m －1m ·m ＋1m －1＝m ＋1m. 当m ＝2时，原式＝2＋12＝32. 【方法归纳】 分式的运算要把握两个关键：一是灵活运用因式分解去通分和约分；二是巧借运算律简化运算．4．化简2a 2－1－1a －1的结果是－1a ＋1． 5．化简：(1＋1x )÷(2x －1＋x 2x)． 解：原式＝x ＋1x ÷2x 2－1－x 2x＝x ＋1x ·x x 2－1＝1x －1.6．先化简(1x －2－2x)·x 2－2x 2，再从0，1，2中选取一个合适的x 的值代入求值． 解：原式＝[x x （x －2）－2（x －2）x （x －2）]·x （x －2）2 ＝x －2（x －2）x （x －2）·x （x －2）2 ＝x －2x ＋42＝－x ＋42. 由于x ≠0且x ≠2，因此只能取x ＝1，所以当x ＝1时，原式＝－x ＋42＝－1＋42＝32.重难点3 分式方程【例3】 分式方程2x －5x －2＝32－x的解是(C ) A ．x ＝－2 B ．x ＝2C ．x ＝1D ．x ＝1或x ＝2【方法归纳】 解分式方程应注意：(1)解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．(2)解分式方程一定注意要验根．7．若x ＝3是分式方程a －2x －1x －2＝0的根，则a 的值是(A ) A ．5 B ．－5 C ．3 D ．－38．(成都中考)已知关于x 的分式方程x ＋k x ＋1－k x －1＝1的解为负数，则k 的取值范围是k ＞12且k ≠1． 9．(广州中考)从广州到某市，可乘坐普通列车或高铁，已知高铁的行驶路程是400千米，普通列车的行驶路程是高铁的行驶路程的1.3倍．(1)求普通列车的行驶路程；(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍，且乘坐高铁所需时间比乘坐普通列车所需时间短3小时，求高铁的平均速度．解：(1)根据题意，得400×1.3＝520(千米)．答：普通列车的行驶路程是520千米．(2)设普通列车平均速度是x 千米/时，根据题意，得520x －4002.5x＝3，解得x ＝120. 经检验，x ＝120是原方程的解，则高铁的平均速度是120×2.5＝300(千米/时)．答：高铁的平均速度是300千米/时．03 备考集训一、选择题(每小题3分，共30分)1．下列式子：－3x ，2a ，x 2－y 2xy ，－a 2π，x －1y 2，a －2b ，其中是分式的个数有(C ) A ．2个 B ．3个C ．4个D ．5个2．将分式2x 2x ＋y中x ，y 的值都扩大10倍，则分式的值(A ) A ．扩大到原来的10倍B ．缩小到原来的110C ．扩大到原来的100倍D ．不变3．分式a x ，x ＋y x 2－y 2，a －b a 2－b 2，x ＋y x －y中，最简分式有(B ) A ．1个 B ．2个 C ．3个 D ．4个4．下列运算正确的是(C )A .－x －y －x ＋y ＝x －y x ＋yB .a 2－b 2（a －b ）2＝a －b a ＋bC .a 2－b 2（a －b ）2＝a ＋b a －bD .x －11－x 2＝1x ＋15．(济南中考)计算2x x ＋3＋6x ＋3，其结果是(A ) A ．2 B ．3C ．x ＋2D ．2x ＋66．(莱芜中考)将数字2.03×10－3化为小数是(C )A ．0.203B ．0.020 3C ．0.002 03D ．0.000 2037．(临沂中考)化简：a ＋1a 2－2a ＋1÷(1＋2a －1)＝(A ) A .1a －1 B .1a ＋1C .1a 2－1D .1a 2＋18．(锦州中考)为了帮助遭受自然灾害的地区重建家园，某学校号召同学们自愿捐款．已知第一次捐款总额为4 800元，第二次捐款总额为5 000元，第二次捐款人数比第一次多20人，而且两次人均捐款额恰好相等．如果设第一次捐款人数为x 人，那么x 满足的方程是(B )A .4 800x ＝5 000x －20B .4 800x ＝5 000x ＋20C .4 800x －20＝5 000xD .4 800x ＋20＝5 000x 9．(牡丹江中考)若2a ＝3b ＝4c ，且abc ≠0，则a ＋b c －2b的值是(B ) A ．2 B ．－2C ．3D ．－310．若分式方程3x x ＋1＝m x ＋1＋2无解，则m ＝(B ) A ．－1 B ．－3C ．0D ．－2二、填空题(每小题3分，共18分)11．当x ＝2时，分式3x －2无意义． 12．(重庆中考)计算：3－8＋(13)－2＋(π－1)0＝8． 13．化简：(2x x －3－x x ＋3)·x 2－9x ＝x ＋9. 14．如图，点A ，B 在数轴上，它们所表示的数分别是－4，4x －45x ＋1，且点A 到原点的距离是点B 到原点距离的2倍，则x ＝－1．15．分式方程1x －1＝a x 2－1的解是x ＝0，则a ＝1． 16．观察规律并填空．(1－122)＝12·32＝34； (1－122)(1－132)＝12·32·23·43＝12·43＝23； (1－122)(1－132)(1－142)＝12·32·23·43·34·54＝12·54＝58； (1－122)(1－132)(1－142)(1－152)＝12·32·23·43·34·54·45·65＝12·65＝35； …(1－122)(1－132)(1－142)…(1－1n 2)＝n ＋12n(用含n 的代数式表示，n 是正整数，且n ≥2)．三、解答题(共52分)17．(12分)计算：(1)(2x －3y 2)－2÷(x －2y)3；解：原式＝14x 6y －4÷x －6y 3＝x 124y 7.(2)4－x x －2÷(x ＋2－12x －2)． 解：原式＝4－x x －2÷(x 2－4x －2－12x －2) ＝4－x x －2÷x 2－4－12x －2＝4－x x －2·x －2（x ＋4）（x －4）＝－1x ＋4.18．(12分)解分式方程：(1)2x x ＋1－1＝1x ＋1； 解：方程两边乘x ＋1，得2x －x －1＝1.解得x ＝2.经检验，x ＝2是原方程的解．(2)x ＋4x （x －1）＝3x －1. 解：方程两边乘x(x －1)，得x ＋4＝3x.解得x ＝2.经检验，x ＝2是原方程的解．19．(9分)(锦州中考)先将(1－1x )÷x －1x 2＋2x化简，然后请自选一个你喜欢的x 值代入求值． 解：原式＝x －1x ÷x －1x 2＋2x＝x －1x ·x （x ＋2）x －1＝x ＋2.当x ＝10时，原式＝10＋2＝12.(注意：x 不能取0，1，－2)20．(9分)对于代数式1x －2和32x ＋1，你能找到一个合适的x 值，使它们的值相等吗？写出你的解题过程．解：能．根据题意，令1x －2＝32x ＋1， 则有2x ＋1＝3(x －2)．解得x ＝7.经检验，x ＝7是1x －2＝32x ＋1的解． 即当x ＝7时，两代数式的值相等．21．(10分)某商家预测一种应季衬衫能畅销市场，就用13 200元购进了一批这种衬衫，面市后果然供不应求，商家又用28 800元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元．(1)该商家购进的第一批衬衫是多少件？(2)若两批衬衫按相同的标价销售，最后剩下50件按八折优惠卖出，如果两批衬衫全部售完利润率不低于25%(不考虑其他因素)，那么每件衬衫的标价至少是多少元？解：(1)设该商家购进的第一批衬衫是x 件，则购进的第二批衬衫是2x 件，由题意可得28 8002x －x13200＝10，解得x ＝120. 经检验x ＝120是原方程的根．答：该商家购进的第一批衬衫是120件．(2)设每件衬衫的标价至少是a元．由(1)得第一批的进价为：13 200÷120＝110(元/件)，第二批的进价为：120元/件．由题意可得120(a－110)＋(240－50)(a－120)＋50(0.8a－120)≥25%×(13 200＋28 800)．解得a≥150.答：每件衬衫的标价至少是150元．。

沪科版七年级下册第九章分式复习（第一课时）【教学目标：】1、通过习题的分析，理解分式的概念、分式的基本性质的应用。

2、把相关的概念与习题相结合，让学生能灵活运用知识点解决相关的问题。

3、会对分式进行约分、通分。

【教学重难点：】重点：分式的基本性质应用难点：分式化简的过程与方法【教学过程：】考点一：分式的概念一般地，如果a，b表示两个整式，并且b中________，那么式子________叫做分式．2．分式有意义的条件是________；分式无意义的条件是________；分式的值为0的条件是________；分式的值为正的条件是________；分式的值为负的条件是________．3．________________统称为有理式．例题分析：本考点共有五题：x 23其中第一题考察分式的基本概念。

(2) 32x(3)xx 22 (4) ∏x (5)x 231-1.下列各式(1)是分式的有 个。

第二题考察分母不能为0 ，二次根式中被开方数要大于或等于零。

2.下列各式中x 取何值时,下列式子有意义.(1)21+-x x (2)11-x (3) (4)第三题通过分母不为0考察非负性 3.下列分式一定有意义的是( )A 21x x + B112++x x C112-+x x D11-x第四题考察字母之间的等量关系4、当 x .y 满足关系 时,分式 y x yx -+22 无意义.第五题考察分母等于零时，分式的取值问题。

5.当x 为何值时,下列分式的值为0?(1) 14+-x x (2)21--x x (3)33--x x (4)12122++-x x x考点二、分式的基本性质1．分式的基本性质：分式的分子与分母都乘以(或除以)_____________________，分式的值不变，即a b ＝a·m b·m ＝a÷mb÷m (________________)．21+-x x 1-x x2．根据分式的基本性质，把一个分式的分子和分母的________叫做分式的约分．约分通常把分式化成最简分式或整式． 3．______________________的分式，叫做最简分式．本考题设计了四题：第一题：直接考察分式的基本性质。

分式复习教学目标：1、复习分式全章知识点2、能熟练运用分式性质、解题技巧等进行分式习题计算3、激发学生学习数学的兴趣，拓展知识面教学重难点：学生对分式性质、解题技巧的理解及应用为重点，教师的恰当引导为难点当堂检测：一、选择题 1、有理式：xx x x x 12,1,21,-+-π中，分式的个数有（ ） A 1个 B 2个 C 3个 D 4个2、使分式42-x x 有意义的x 的取值范围是（ ） A 2=x B 2≠x C 2-=x D 2-≠x3、把分式y x yx +-中的字母x 、y 的值都扩大10倍，则分式的值（ ）A 扩大10倍B 缩小10倍C 不变D 扩大100倍4、 分式1a b -，1a b +，221a b -的最简公分母是（ ）A ．22()()a b a b +-B ．22a b -C ．222()a b -D ．2()()a b a b +-5、若P=n m，Q=11++n m ，n m <且m 、n 均为正整数，则P 、Q 的大小关系是（） A P>Q B P=Q C P<Q D 不能确定6、解分式方程2236111x x x +=+--,分以下四步,其中,错误的一步是( )A.方程两边分式的最简公分母是(x-1)(x+1)B.方程两边都乘以(x-1)(x+1),得整式方程2(x-1)+3(x+1)=6C.解这个整式方程,得x=1D.原方程的解为x=17、银原子的直径为0.0003微米，用科学记数表示为( )（A ）4103⨯微米；（B ）4103-⨯微米；（C ）3103-⨯微米；（D ）3103.0-⨯微米．二、填空题1、当 时，分式2255x x --的值为0．2、填空：()366a ab a =+（0≠b ）； ()22.42x x y x y =-+ 3、下列分式中，最简分式有 个．2124b c a ，25()x y y x ++，223()a b a b +，2242a b a b --，a b b a--，222x x x --． 4、计算201()(5)5----=___________________三、计算题（1）、22543()125y x y xy x ⋅÷- （2）、2422x x x +--（3）、1111()()x y x y -----÷+ （4）、解方程：33122x x x-+=--。