圆周运动绳杆模型讲解学习

竖直面内三种圆周运动模型精讲精练模型球-绳模型【知识点精讲】球-绳模型实例球与绳连接在竖直面内圆周运动球沿竖直面圆周内轨道运动图示最高点无支撑最高点无支撑最高点受力特征重力、弹力，弹力方向向下或等于零重力、弹力，弹力方向向下、等于零或向上受力示意图力学特征mg+F N=mv2r临界特征F N=0，v min=gr过最高点条件v≥gr速度和弹力关系讨论分析①恰好过最高点时，v=gr，mg=mv2r，F N=0，绳、轨道对球无弹力②能过最高点时，v≥gr，F N+mg=mv2r，绳、轨道对球产生弹力F N③不能过最高点时，v<gr，在到达最高点前小球已经脱离了圆轨道做斜抛运动【方法归纳】(1)定模型：首先判断是轻绳模型还是轻杆模型，两种模型物体过最高点的临界条件不同．(2)确定临界点：抓住球-绳模型中球恰好能过最高点时v=gR的临界条件．(3)研究状态：通常情况下竖直平面内的圆周运动只涉及最高点和最低点的运动情况．(4)受力分析：对物体在最高点或最低点时进行受力分析，根据牛顿第二定律列出方程：F合=F向．(5)过程分析：应用动能定理或机械能守恒定律将初、末两个状态联系起来列方程．【针对性训练】1(2018•高考全国卷Ⅲ)如图，在竖直平面内，一半径为R的光滑圆弧轨道ABC和水平轨道P A在A 点相切。

BC为圆弧轨道的直径。

O为圆心，OA和OB之间的夹角为α，sinα=35，一质量为m的小球沿水平轨道向右运动，经A点沿圆弧轨道通过C点，落至水平轨道；在整个过程中，除受到重力及轨道作用力外，小球还一直受到一水平恒力的作用，已知小球在C点所受合力的方向指向圆心，且此时小球对轨道的压力恰好为零。

重力加速度大小为g。

求：(1)水平恒力的大小和小球到达C点时速度的大小；(2)小球到达A点时动量的大小；(3)小球从C点落至水平轨道所用的时间。

2(12分)(2020新高考冲刺仿真模拟)某兴趣小组设计了一个玩具轨道模型如图甲所示，将一质量为m=0.5kg的玩具小车(可以视为质点)放在P点，用弹簧装置将其从静止弹出(弹性势能完全转化为小车初始动能)，使其沿着半径为r=1.0m的光滑圆形竖直轨道OAO′运动，玩具小车与水平面PB的阻力为其自身重力的0.5倍(g取10m/s2)，PB=16.0m，O为PB中点．B点右侧是一个高h=1.25m，宽L= 2.0m的壕沟．求：(1)要使小车恰好能越过圆形轨道的最高点A，小车在O点受到轨道弹力的大小；(2)要求小车能安全越过A点，并从B点平抛后越过壕沟，则弹簧的弹性势能至少为多少？(3)若在弹性限度内，弹簧的最大弹性势能E pm=40J，以O点为坐标原点，OB为x轴，从O到B方向为正方向，在图乙坐标上画出小车能进入圆形轨道且不脱离轨道情况下，弹簧弹性势能E p与小车停止位置坐标x关系图．3(2024年5月四川宜宾质检)如图所示，在距地面上方h的光滑水平台面上，质量为m=4kg的物块左侧压缩一个轻质弹簧，弹簧与物块未拴接。

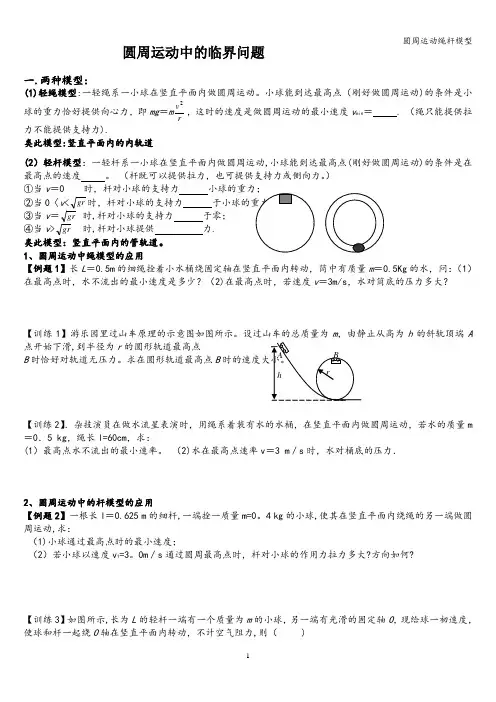
圆周运动绳杆模型1圆周运动中的临界问题一.两种模型:(1)轻绳模型:一轻绳系一小球在竖直平面内做圆周运动。

小球能到达最高点（刚好做圆周运动)的条件是小球的重力恰好提供向心力，即mg ＝m rv 2，这时的速度是做圆周运动的最小速度v min ＝ . （绳只能提供拉力不能提供支持力).类此模型:竖直平面内的内轨道(2）轻杆模型：一轻杆系一小球在竖直平面内做圆周运动,小球能到达最高点(刚好做圆周运动)的条件是在最高点的速度 。

（杆既可以提供拉力，也可提供支持力或侧向力。

） ①当v ＝0 时，杆对小球的支持力 小球的重力；②当0〈v <gr 时，杆对小球的支持力 于小球的重力；③当v ＝gr时,杆对小球的支持力 于零； ④当v >gr 时,杆对小球提供 力. 类此模型：竖直平面内的管轨道。

1、圆周运动中绳模型的应用【例题1】长L ＝0.5m 的细绳拴着小水桶绕固定轴在竖直平面内转动，筒中有质量m ＝0.5Kg 的水，问：（1）在最高点时，水不流出的最小速度是多少？（2)在最高点时，若速度v ＝3m/s ，水对筒底的压力多大？【训练1】游乐园里过山车原理的示意图如图所示。

设过山车的总质量为m ，由静止从高为h 的斜轨顶端A 点开始下滑,到半径为r 的圆形轨道最高点B 时恰好对轨道无压力。

求在圆形轨道最高点B【训练2】．杂技演员在做水流星表演时，用绳系着装有水的水桶，在竖直平面内做圆周运动，若水的质量m ＝0．5 kg ，绳长l=60cm ，求：(1）最高点水不流出的最小速率。

（2)水在最高点速率v ＝3 m ／s 时，水对桶底的压力．2、圆周运动中的杆模型的应用 【例题2】一根长l ＝0.625 m 的细杆,一端拴一质量m=0。

4 kg 的小球,使其在竖直平面内绕绳的另一端做圆周运动,求：（1)小球通过最高点时的最小速度；（2）若小球以速度v 1=3。

0m ／s 通过圆周最高点时，杆对小球的作用力拉力多大?方向如何?【训练3】如图所示,长为L 的轻杆一端有一个质量为m 的小球，另一端有光滑的固定轴O ，现给球一初速度，使球和杆一起绕O 轴在竖直平面内转动，不计空气阻力,则（ )2vR A 。

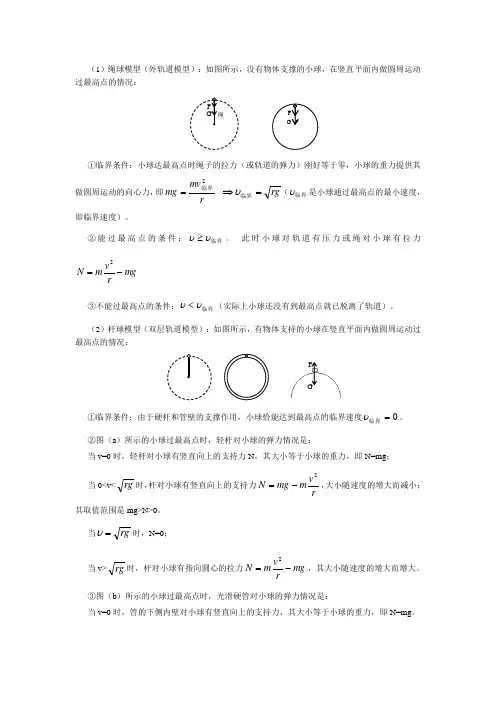
（1）绳球模型（外轨道模型）：如图所示，没有物体支撑的小球，在竖直平面内做圆周运动过最高点的情况：①临界条件：小球达最高点时绳子的拉力（或轨道的弹力）刚好等于零，小球的重力提供其做圆周运动的向心力，即rmvmg2临界=⇒rg=临界υ（临界υ是小球通过最高点的最小速度，即临界速度）。

②能过最高点的条件：临界υυ≥。

此时小球对轨道有压力或绳对小球有拉力mgrvmN-=2③不能过最高点的条件：临界υυ<（实际上小球还没有到最高点就已脱离了轨道）。

（2）杆球模型（双层轨道模型）：如图所示，有物体支持的小球在竖直平面内做圆周运动过最高点的情况：①临界条件：由于硬杆和管壁的支撑作用，小球恰能达到最高点的临界速度0=临界υ。

②图（a）所示的小球过最高点时，轻杆对小球的弹力情况是：当v=0时，轻杆对小球有竖直向上的支持力N，其大小等于小球的重力，即N=mg；当0<v<rg时，杆对小球有竖直向上的支持力rvmmgN2-=，大小随速度的增大而减小；其取值范围是mg>N>0。

当rg=υ时，N=0；当v>rg时，杆对小球有指向圆心的拉力mgrvmN-=2，其大小随速度的增大而增大。

③图（b）所示的小球过最高点时，光滑硬管对小球的弹力情况是：当v=0时，管的下侧内壁对小球有竖直向上的支持力，其大小等于小球的重力，即N=mg。

GF当0<v<rg 时，管的下侧内壁对小球有竖直向上的支持力rv m mg N 2-=，大小随速度的增大而减小，其取值范围是mg>N>0。

当v=gr 时，N=0。

当v>gr 时，管的上侧内壁对小球有竖直向下指向圆心的压力mg rv m N -=2，其大小随速度的增大而增大。

④图(c)的球沿球面运动，轨道对小球只能支撑，而不能产生拉力。

在最高点的v 临界=gr 。

当v=gr 时，小球将脱离轨道做平抛运动。

教师辅导讲义 学员编号：1年 级：高一年级 课 时 数： 学员姓名： 辅导科目：物理 学科教师：授课类型T 同步(圆周运动绳杆模型)授课日期及时段 教学内容一.描述圆周运动的各物理量间的关系1．线速度v 、角速度ω以及周期T 之间的关系：v ＝ωr ＝2πr T. 2．角速度ω与转速n 的关系：ω＝2πn (注：n 的单位为r/s)．二.匀速圆周运动1．特征：(1)线速度的大小不变，方向时刻改变．(2)向心力大小不变，方向始终指向圆心．(3)向心加速度大小不变，方向始终指向圆心．2．向心力：F ＝m v 2r ＝m ω2r ＝m 4π2T2r . 3．向心加速度：a ＝v 2r ＝ω2r ＝4π2T2r . 三.描述圆周运动的各物理量间的关系描述圆周运动的物理量有线速度、角速度、周期、转速等，它们之间的关系为：ω＝2πT ＝2πn ，v ＝ωr ＝2πTr 同步知识梳理T 同步——绳杆模型＝2πrn ，这些关系不仅在物体做匀速圆周运动中适用，在变速圆周运动中也适用，此时关系式中各量是瞬时对应的．四.向心力的来源分析向心力可以是弹力、摩擦力，也可以是物体受到的合外力或某个力的分力，但只有在匀速圆周运动中，向心力才等于物体所受的合外力，在变速圆周运动中，向心力不等于物体所受到的合外力，而是等于物体沿圆心方向的合外力．五.竖直面内的“绳杆模型”的临界问题1.轻绳模型(如图所示)(1)绳内(内轨道)施力特点：只能施加向下的拉力(或压力)．(2)在最高点的动力学方程T ＋mg ＝m v 2r. (3)在最高点的临界条件T ＝0，此时mg ＝m v 2r，则v ＝gr . ①v ＝gr 时，拉力或压力为零．②v >gr 时，小球受向下的拉力或压力．③v <gr 时，小球不能达到最高点．即轻绳的临界速度为v 临＝gr .2.轻杆模型(如图所示)(1)杆(双轨道)施力特点：既能施加向下的拉力，也能施加向上的支持力．(2)在最高点的动力学方程当v ＞gr 时，N ＋mg ＝m v 2r，杆对球有向下的拉力，且随v 增大而增大． 当v ＝gr 时，mg ＝m v 2r，杆对球无作用力． 当v ＜gr 时，mg －N ＝m v 2r，杆对球有向上的支持力． 当v ＝0时，mg ＝N ，球恰好到达最高点．(3)杆类的临界速度为v 临＝0.（2020·定远县育才学校高二开学考试）在质量为M 的电动机飞轮上固定着一个质量为m 的重物，重物到转轴的距离为r ，如图所示，为了使放在地面上的电动机不会跳起，电动机飞轮的角速度不能超过（ ）A ．M m g mr +B ．M m g mr +C ．M m g mr -D ．Mg mr【解析】解：重物转到飞轮的最高点时，电动机刚要跳起时，重物对飞轮的作用力F 恰好等于电动机的重力Mg ，即F=Mg．以重物为研究对象，由牛顿第二定律得Mg+mg=mω2r ，解得ω=m M g mr +（2020·江苏镇江市·高一期中）如图所示，长为L 的悬线固定在O 点，在O 点正下方2L 处有一钉子C ，把悬线另一同步题型分析端的小球m 拉到跟悬点在同一水平面上无初速度释放，小球到悬点正下方时悬线碰到钉子时，那么小球的（ ） A ．线速度突然增大B ．角速度突然增大C ．向心加速度突然增大D ．悬线拉力突然增大【解析】A ．碰到钉子瞬间，线速度不突变，所以线速度不变，A 错误；B ．碰到钉子瞬间，圆周运动半径减小，根据v r ω=可知角速度突然增大，B 正确；C ．碰到钉子瞬间，圆周运动半径减小，根据2v a r =可知向心加速度增大，C 正确；D ．根据牛顿第二定律可知 T mg ma -=小球重力不变，向心加速度增大，悬线拉力增大，D 正确。

圆周运动中绳模型和杆模型的一般解析一：绳模型：若已不可伸长的绳子长L ，其一端栓有一质量m 的小球（可看成质点）。

现使绳子拉着小球绕一点O 做匀速圆周运动，则（1）小球恰好通过最高点的速度v 。

(2)当能通过最高点时，绳子拉F 。

解：（1）小球恰能通过最高点的临界条件是绳子没有拉力， 则对小球研究，其只受重力mg 作用，故，由其做圆周运动得:L v m mg 2= 故 gL v =(2)由分析得，当小球到最高点时速度gL v v =>'时，则，mg Lmv F -=2' 而，当gL v v =<'时，那么小球重力mg 大于其所需向心力，因此小球做向心运动。

二：杆模型：若一硬质轻杆长L ，其一端有一质量m的小球（可看成质点）。

现使杆和小球绕一点O 做匀速圆周运动， 则 （1）小球恰好通过最高点的速度v 。

(2)当能通过最高点时，杆对小球的作用力F 。

解：（1）因为杆具有不可弯曲不可伸长的性质，所以小球在最高点，当速度为0时，恰好能通过。

（2）①由绳模型可知，当小球通过最高点速度gL v =时，恰好有绳子拉力为0，则同理可知，当杆拉小球到最高点时， 若小球速度gL v =时，小球所需向心力恰好等于重力mg ， 故，此时杆对小球没有作用力。

②当小球通过最高点时速度gL v >时，则小球所需向心力比重力mg 大，所以此时杆对小球表现为拉力，使小球不至于做离心运动故对小球有， L mv mg F 2=+③同理，当小球通过最高点时速度gL v <时，则小球所需向心力小于重力mg ，所以此时小球对杆有压力作用，有牛顿第三定律得，杆对小球表现为支持力作用，故对小球有， L mv F mg 2=-。

第19讲竖直面内圆周运动之绳”模型和“杆”模型及其临界问题1．（2022·江苏）在轨空间站中物体处于完全失重状态，对空间站的影响可忽略．空间站上操控货物的机械臂可简化为两根相连的等长轻质臂杆，每根臂杆长为L．如图1所示，机械臂一端固定在空间站上的O点，另一端抓住质量为m的货物．在机械臂的操控下，货物先绕O点做半径为2L、角速度为ω的匀速圆周运动，运动到A点停下．然后在机械臂操控下，货物从A点由静止开始做匀加速直线运动，经时间t到达B点，A、B间的距离为L。

（1）求货物做匀速圆周运动时受到的向心力大小F n。

（2）求货物运动到B点时机械臂对其做功的瞬时功率P。

（3）在机械臂作用下，货物、空间站和地球的位置如图2所示，它们在同一直线上．货物与空间站同步做匀速圆周运动．已知空间站轨道半径为r，货物与空间站中心的距离为d，忽略空间站对货物的引力，求货物所受的机械臂作用力与所受的地球引力之比F1：F2。

【解答】解：（1）货物做匀速圆周运动，向心力F n=m⋅2Lω2=2mLω2（2）设货物到达B点的速度为v，根据匀变速规律L=v2t，得v=2L t货物的加速度a=vt=2Ltt=2Lt2根据牛顿第二定律，机械臂对货物的作用力F＝ma=2mL t2机械臂对货物做功的瞬时功率P＝Fv=2mLt2×2L t=4mL2t3（3）设地球质量为M，空间站的质量为m0，地球对空间站的万有引力为F，根据万有引力定律F=G Mm0 r2①地球对货物的万有引力F 2=G Mm(r−d)2②联立①②得m 0m=Fr 2F 2(r−d)2③设空间站做匀速圆周运动的角速度为ω0，根据牛顿第二定律对空间站F =m 0rω02④ 对货物F 2−F 1=m(r −d)ω02⑤联立③④⑤解得F 1F 2=r 3−(r−d)3r 3答：（1）货物做匀速圆周运动时受到的向心力大小为2m ω2L ； （2）货物运动到B 点时机械臂对其做功的瞬时功率为4mL 2t 3；（3）货物所受的机械臂作用力与所受的地球引力之比为r 3−(r−d)3r 3。

圆周运动中的临界问题一.两种模型:(1)轻绳模型：一轻绳系一小球在竖直平面内做圆周运动.小球能到达最高点(刚好做圆周运动)的条件是小球的重力恰好提供向心力，即mg ＝m rv 2，这时的速度是做圆周运动的最小速度v min ＝ . （绳只能提供拉力不能提供支持力）. 类此模型：竖直平面内的内轨道(2)轻杆模型：一轻杆系一小球在竖直平面内做圆周运动，小球能到达最高点(刚好做圆周运动)的条件是在最高点的速度 . （杆既可以提供拉力，也可提供支持力或侧向力.） ①当v ＝0 时，杆对小球的支持力 小球的重力； ②当0<v <gr 时，杆对小球的支持力于小球的重力；③当v＝gr 时，杆对小球的支持力 于零； ④当v >gr 时，杆对小球提供 力. 类此模型：竖直平面内的管轨道.1、圆周运动中绳模型的应用 【例题1】长L ＝0.5m 的细绳拴着小水桶绕固定轴在竖直平面内转动，筒中有质量m ＝0.5Kg 的水，问：（1）在最高点时，水不流出的最小速度是多少？（2）在最高点时，若速度v ＝3m/s ，水对筒底的压力多大？【训练1】游乐园里过山车原理的示意图如图所示。

设过山车的总质量为m ，由静止从高为h 的斜轨顶端A 点开始下滑，到半径为r 的圆形轨道最高点B 时恰好对轨道无压力。

求在圆形轨道最高点B 时的速度大小。

【训练2】．杂技演员在做水流星表演时，用绳系着装有水的水桶，在竖直平面内做圆周运动，若水的质量m ＝0．5 kg ，绳长l=60cm ，求：(1)最高点水不流出的最小速率。

(2)水在最高点速率v ＝3 m ／s 时，水对桶底的压力．2、圆周运动中的杆模型的应用【例题2】一根长l ＝0.625 m 的细杆，一端拴一质量m=0.4 kg 的小球，使其在竖直平面内绕绳的另一端做圆周运动，求：(1)小球通过最高点时的最小速度；(2)若小球以速度v 1=3.0m ／s 通过圆周最高点时，杆对小球的作用力拉力多大?方向如何？vR 【训练3】如图所示，长为L 的轻杆一端有一个质量为m 的小球，另一端有光滑的固定轴O ，现给球一初速度，使球和杆一起绕O 轴在竖直平面内转动，不计空气阻力，则（ ） A.小球到达最高点的速度必须大于gLB .小球到达最高点的速度可能为0 C.小球到达最高点受杆的作用力一定为拉力 D.小球到达最高点受杆的作用力一定为支持力【训练4】如图所示，在竖直平面内有一内径为d 的光滑圆管弯曲而成的环形轨道，环形轨道半径R 远远大于d ，有一质量为m 的小球，直径略小于d ，可在圆管中做圆周运动。