上海教育出版社六年级第一章数的整除复习提纲

第1讲 整数和整除【学习目标】整数和整除是六年级数学上学期第一章第一节内容，主要对整数的分类和整除的概念进行讲解，重点是整除的概念理解，难点是整除条件的归纳总结．通过这节课的学习一方面为我们后期学习公因数和公倍数提供依据，另一方面也为后面学习有理数奠定基础．【基础知识】1.⎧⎫⎪⎬⎨⎭⎪⎩正整数自然数整数零负整数； 2.整除：整数a 除以整数b ，若除得的商是整数且余数为零. 即称：a 能被b 整除；或b 能整除a.整除的条件：..⎫⎧⎪⎨⎬⎪⎩⎭除数、被除数都是整数；三整一零商是整数且余数为零整除与除尽的关系.⎧⎧⎪⎨⎨⎩⎪⎩整除：被除数、除数、商整数，且余数为零；区别除尽：被除数、除数、商是整数，没有余数.联系：整除是除尽都是不一定的特殊形式3.因数与倍数：整数a 能被整数b 整除，a 就叫b 的倍数，b 就叫a 的因数（约数）.因数与倍数的特征：⎧⎪⎨⎪⎩因数与倍数互相依存；一个整数的因数中最小因数为1，最大因数为它本身一个整数的倍数中最小的倍数是它本身，无最大倍数.4.能被2整除的数2468.⎧⎨⎩偶数(2n)；(否则是奇数(2n-1))特征：个位上是0，，，，，能5整除的数的特征：个位上数字是0，5； 能同时被2、5整除的数：个位上数字是0.*能被3整除的数：一个整数的各个数位上数字之和能被3整除，这个整数就能被3整除. *能同时被2、3和5整除的数：个位数是0，且各个数位上数字之和能被3整除.【考点剖析】考点一：整数的意义和分类例1．判断题（若是正确的，请说明理由；若是错误的，请把它改正确）．（1）最小的自然数是1 ； （2）最小的整数是0；（3）非负整数是自然数；（4）有最大的正整数，但没有最小的负整数；（5）有最小的正整数，但没有最大的负整数．【难度】★【答案】（1）×；（2）×；（3）√；（4）×；（5）×．【解析】（1）错误，最小的自然数是0；（2）错误，不存在最小的整数；（3）正确；（4）错误，既没有最大的正整数，也没有最小的负整数；（5）错误，最小的正整数是1，最大的负整数是－1．【总结】本题主要考查与整数有关的概念．例2把下列各数放入相应的圈内：15，－1，－0.2，0，－63，0.7，13，－0.2323…，35．【难度】★【答案】整数：15，－1，0，－63，13；自然数：15，0，13；正整数：15，13；负整数：－1，－63．【解析】整数包括正整数、零、负整数；自然数包括正整数和零．【总结】本题主要考查整数的分类．例3（1）试说说正整数、负整数、零、自然数、整数之间的关系；（2）试比较正整数、负整数、零的大小；（3）试比较负整数、自然数的大小．【难度】★★【答案】（1）整数包括正整数、零、负整数；自然数包括正整数和零；（2）正整数大于0，负整数小于0，正整数大于负整数；（3）自然数大于负整数；例4五个连续的自然数，已知中间数是a，那么其余四个数分别是______、______、______、______．若这五个连续自然数的和是20，试求这五个数．【难度】★★【答案】2112、、、．这五个数是：2、3、4、5、6．a a a a--++【解析】列方程：(2)(1)(1)(2)20-+-+++++=a a a a a解得：4a=∴这五个数是：2、3、4、5、6．【总结】本题主要考查如何利用已知的字母去表示与其连续的整数．考点二：整除的意义例1．老师问：“当 4.5b=时，a能被b整除吗？”a=时，0.9一个同学回答：“因为商是5，是整数，所以a能被b整除．”你认为对吗？【难度】★【答案】不对【解析】整除要求被除数、除数、商是整数，且余数是零；本题只满足了商是整数，余数是0，忽略了对被除数、除数的要求；【总结】本题主要考查整除所满足的条件．例2下列各组数中，如果第一个数能被第二个数整除，请在下面的（）内打“√”，不能整除的打“×”．18和9（）15和30（）0．4和4（）14和6（）17和35（）9和0．5（）【难度】★【答案】横向：√×××××【解析】整除的意义：整数a除以整数b，如果除得的商是整数而余数为零，我们就说a能被b整除；或者说b能整除a．只有18和9满足；【总结】本题主要考查整除所满足的条件．师生总结1、整除的条件是什么？2、“a能整除b”与“a能被b整除”的区别是什么？归纳总结1．除数、被除数都是整数；2．被除数除以除数，商是整数而且没有余数.归纳总结整数a除以整数b，如果除得的商正好是整数而没有余数，我们就说a能被b整除，或者说b能整除a。

六上数学课堂笔记第一章数的整除1.1整数和整除的意义整除：整数a 除以整数b，如果除得的商是整数而余数为零，我们就说a 能被b 整除；或者说b 能整除a。

c b a =÷（a、b、c 都是整数，且0≠b ）整除是除尽的一种特殊情况。

凡是整除的一定能除尽，但能除尽的不一定能整除。

1.2因数和倍数因数和倍数：整数a 能被整数b 整除，a 叫做b 的倍数，b 叫做在a 的因数。

求一个因数的方法：一对一对的找（1）列乘法算式。

1×18=18.2×9=18.3×6=18（2）列除法算式。

18÷1=18.18÷2=9.18÷3=6思考：如何既不重复，又不遗漏的找出所有的因数？试找出所有36的因数。

36=1×36=2×18=3×12=4×9=6×6从小到大依次写出1,2,3,4,6,9,12,18,36.2的倍数可以表示为2n，n 为正整数。

0既不是正整数，也不是负整数。

0是最小的自然数。

最大的负整数是-1，最小的正整数是1.三整一零才整除3.16.2÷×不是整数。

6÷4×余数不为0.除法算式从前往后按顺序说的一定是能被整除，倒过来的则是能整除。

428=÷，8能被2整除，2能整除8。

1、正整数的范围中。

2、整除的基础上。

3、相互依存。

4、一个数的因数是有限个。

最小为1，最大为本身。

一个数的因数通常是成对出现的。

（平方数除外）5、一个数的倍数有无限个。

最小为本身，最大无。

6、一个整数的最大因数和最小倍数相等，都等于本身。

1.3能被2,5整除的数能被2整除的数的特征：个位上是0、2、4、6、8的数都能被2整除。

正整数按照能否被2整除分类：正整数⎩⎨⎧偶数奇数能被5整除的数的特征：个位上是0或5的数，都能被5整除。

能同时被2和5整除的数的特征：个位上是0的数1.4（1）素数、合数只含有因数1和本身的整数叫做素数或质数，如果除了1和它本身还有别的因数，这样的数叫做合数。

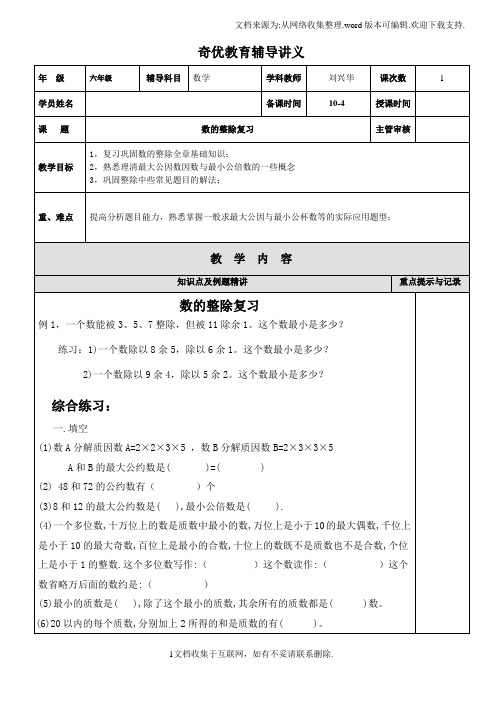
（4）非负整数是自然数。

（）（5）如果a能被b整除，那么a是b的倍数，b是a的因数。

（）7.乐乐家要装修新房子，地面是长3.2米、宽2.8米的长方形，准备用正方形的地砖铺满。

现有地砖尺寸是30×30、40×40（单位：厘米）的两种尺寸，你觉得用那一种比较合适，为什么？8.从下列数中选择适当的数填入相应的圈内：-25、13、 2.47、-8.75、0、29.自然数正整数负整数整数9.从下列算式中选择适当的算式填入相应的圈内：25÷5=5，2.5÷0.5=5，25÷3=8……1，25÷4=6.25整除除尽10.指出第一行的各数能被第二行的哪些数整除。

48 30 91 1202 3 5 78.三个素数的和为140，求这三个素数的乘积的最大值。

9.在1，2，3，…，2000这2000个自然数中，有 个自然数能同时被2和3整除，而且不能被5整除．10.五位数 是9的倍数，其中是4的倍数，那么的最小值是 ．11，有三个连续的自然数，它们的平均数能分别被三个不同的质数整除。

要使它们的和最小，这三个自然数分别是多少？,自我测试1，；两个数的最大公因数是1，最小公倍数是91，那么这两个数是 和 或 和 。

2，甲=A ⨯⨯52，乙=A ⨯⨯72，甲、乙两个数的最小公倍数是210，A 是 。

3，一个数减去2能被5整除，加上4能被6整除，这个数最小是几？4，由0，3，5写成的没有重复数字的三位数中，有哪些能被5整除？5，下面的连乘积中，末尾有多少个0？1×2×3×…×29×306，将1至9九个数字写在一条纸带上，如下图：将它剪成三段，每段上数字联在一起算一个数，把这三个数相加，使和能被77整除，那么中间一段的数是____。

（1998年全国小学数学奥林匹克决赛试题）。

上海教育版六上第一章《数的整除》word教案第一章：数的整除整理与复习（2）一、知识树质数与合数-----分解质因数律数（约数）公因数----最大公因数----互质数整除V 能被2整除的数的特征---奇数与偶数能被3、5整除的数的特征倍数——公倍数-----最小公倍数知识的应用：1、求一个数的约数和倍数2、自然数的分类，质数和合数、奇数和偶数的判断。

3、用短除法分解质因数4、求最大公因数和最小公倍数应用题：最大公因数和最小公倍数的应用题二、有关的定义1、整除的概念（上学期的知识）整数a除以整数b（b=0）,除得的商正好是整数而没有余数，我们就说a能被b整除，或者b能整除a。

能被2整除的数的特征：个位上是0、2、4、6、8的数能被5整除的数的特征：个位上是0或5的数能被3整除的数的特征：各个位上数的和能被3整除，这个数就能被3整除。

能被2整除的数叫做偶数，不能被2整除的数叫做奇数。

2、数a能被数b整除，a就叫做b的倍数，b就叫做a的约数。

一个数的约数的个数是有限的，最小的约数是1，最大的约数是它本身。

一个数的倍数的个数是无限的，最小的倍数是它本身，没有最大的倍数。

3、一个数除了1和它本身以外，不再有别的因数，这个数叫质数。

一个数除了1和它本身以外，还有别的因数，这个数叫合数。

“ 1 ”即不是素数，也不是合数。

4、把一个合数用质因数相乘的形式表示出来，叫做分解素因数。

5、几个数公有的约数叫做这几个数的公约数，其中最大一个叫这几个数的最大公约数。

几个数公有的倍数叫做这几个数的公倍数，其中最小的一个叫这几个数的最小公倍数。

公约数只有1的两个数叫互质数互质数由两个合数组成：8和9, 一个合数，一个质数：3和4，两个质数：2和3三、练习：按内容复习一、复习约数和倍数的意义1、什么叫做约数？什么叫做倍数? 2 、以24十8= 3说说谁是谁的约数？谁是谁的倍数?3、判断题。

(1)因为15能被3整除，所以说15是倍数，3是约数。

上海市六年级第一学期数学知识点整理第一章数的整除1、零和正整数统称为自然数。

正整数、零、负整数统称为整数。

自然数2、整数a除以整数b,如果除得的商是整数而余数为零，我们就说a能被b整除，或者说b 能整除a。

式子表示：如果a÷ b=c（ a、b，C都为整数）称a能被b整除或b能整除a。

（区分两种表述）3、整除的条件：1）除数，被除数都为整数2）被除数除以除数，商是整数而且余数为零。

例如：48 ÷ 8=6 整除6 ÷ 4=1.5 非整除4、因数与倍数整数a能被整数b整除，a叫做b的倍数，b叫做a的因数。

因数和倍数是相互依存的。

5、素数（也叫质数）是一个正整数，如果只有1和它本身两个因数。

2, 3, 5, 7, 11…2是偶数中唯一的素数；合数是如果除了1和它本身以外还有别的因数的。

4,6,8,10,12…..1既不是素数，也不是合数。

正整数又可以分为1、素数和合数。

素因数是每个合数都可以写成几个素数相乘的形式，其中每个素数都是这个合数的因数。

分解素因数是把一个合数用素因数相乘的形式表示出来。

公因数是几个数共有的因数。

最大公因数是其中最大的一个公因数。

如果两个整数只有公因数1,那么称这两个数互素。

两个整数中，如果某个数是另一个数的因数，那么这个数就是这两个数的最大公因数。

如果这两个数互素，那么它们的最大公因数就是1。

6、几个整数的公有的倍数叫做它们的公倍数。

其中最小的一个叫做它们的最小公倍数。

例题3求30 ¾ 45 最丈仝因数和贵小公倍数”解3 30 45 ｛甲公有的素因数3除）515 （用公有的素因数5除）刁—刁― （除到两个商互素为止）30和轩的最大公因数是3 X 5= 15?却和45的最小公倍数是3 X 5×2×3^90.求两个整数的最小公倍数，只要取它们所有公有的素因数，再取它们各自剩余额素因数,将这些数连乘，所得的积就是这两个数的最小公倍数。

精心整理奇优教育辅导讲义年级六年级辅导科目数学学科教师刘兴华课次数 1学员姓名备课时间10-4授课时间课题数的整除复习主管审核教学目标1，复习巩固数的整除全章基础知识；2，熟悉理清最大公因数因数与最小公倍数的一些概念3，巩固整除中些常见题目的解法；重、难点提高分析题目能力，熟悉掌握一般求最大公因与最小公杯数等的实际应用题型；教学内容知识点及例题精讲重点提示与记录数的整除复习例1，一个数能被3、5、7整除，但被11除余1。

这个数最小是多少？练习：1)一个数除以8余5，除以6余1。

这个数最小是多少？2)一个数除以9余4，除以5余2。

这个数最小是多少？综合练习：一.填空(1)数A分解质因数A=2×2×3×5，数B分解质因数B=2×3×3×5A和B的最大公约数是()=()(2)48和72的公约数有（）个(3)8和12的最大公约数是(),最小公倍数是().(4)一个多位数,十万位上的数是质数中最小的数,万位上是小于10的最大偶数,千位上是小于10的最大奇数,百位上是最小的合数,十位上的数既不是质数也不是合数,个位上是小于1的整数.这个多位数写作:（）这个数读作:（）这个数省略万后面的数约是:（）(5)最小的质数是(),除了这个最小的质数,其余所有的质数都是()数。

(6)20以内的每个质数,分别加上2所得的和是质数的有()。

(7)最小的合数除以最小的质数的商加上最小的既是质数又是奇数(奇质数),和是()。

(8)把120质因数有（）。

（9）一个数是20的倍数，又是60的约数。

这个数可能是()，又可能是() （10）．已知a、b是自然数，且b＝a＋1，则a和b的最大公约数是()，最小公倍数是()。

（11）周燕有一盒巧克力糖，7粒一数还余4个，5粒一数又少3个，3粒一数正好没剩余，这盒巧克力至少有（）粒（12）甲、乙两个数的最大公约数是15，最小公倍数是90。

整除一、整数：0⎧⎪⎫⎨⎬⎪⎭⎩整整自然正整负数数数数二、整除（1）整数．．a 除以整数．．b （b ≠0），商是整数．．，余数是0，我们说a 能被b 整除。

（2） a 除以b ＝b 除a ＝a 被b 除．（★解题中，全部化成：“a 被b 整除”模型）三、 除尽：（1）数a 除以数b ，商是整数．．或有限小数．．．．。

我们说a 能被b 除尽。

（★只看商） （2）整除一定能除尽，除尽不一定能整除。

【例 1】 (1)下列说法正确的是（ ）A 、一个整数，不是正整数，就是负整数；B 、0不是自然数；C 、1是最小的自然数；D 、0既不是正整数，也不是负整数；（2） 最小的正整数是 _________，最大的正整数 __________最小的负整数是 _________，最大的负整数 __________最小的非负整数是 ，最大的非正整数是___________最小的自然数是_________第一讲 数的整除【例 2】 【基础】下列说法正确的是（ ）A 、24能被5整除B 、16能整除8C 、4能被36整除D 、15能整除75【提高】a 能整除28，则a 一定是（ ）A 、28、56等等这些28的整数倍的数B 、4或7C 、2、4、7、14或28D 、1、2、4、7、14或28【尖子】根据下列各除式商的情况，将各除式的编号填入相应的横线上：①19÷4 ②40÷3 ③ 6.4÷1.6 ④ 52÷13 ⑤30÷7 ⑥17÷68 ⑦2÷3除尽：____________________ 整除：___________________除不尽：__________________四、整除的特征：（1） 能被2整除的数的末位是：0，2，4，6，8.能被5整除的数的末位是：0、5能同时被2、5整除的数的末位是0 （★看：末位）（2） 能被 3整除：各数位之和能被3整除.能被9整除，：各数位之和能被9整整除 （★看：各数位之和）（3）能被2整除的整数叫偶数，不能被2整除的整数叫奇数.【例 3】 【基础】（1）正整数中，最小的奇数是__________；最小的偶数是_________；（2）能被2整数的最大2位数是 ，最小的两位数是（3） 能被5整数的最大的两位偶数是 ，最小的两位奇数是_____（4）能同时被2、5整除的最大的两位数是 ，最小两位数是______【提高】（1） 237至少加上 ，所得的数才能同时被2、5整除；（2） 488至少减少 ，所得的数才能同时被2、5整除.（3）521至少加上 ，所得的数才能同时被2、3、5整除.偶数+偶数=偶数奇数+偶数=奇数奇数+奇数=偶数偶数×偶数=偶数奇数×偶数=偶数奇数×奇数=奇数性质：【尖子】从0，5，6，7四个数中任选3个（不能重复）数字，按下列要求排成一个数（1）能被2整除的的最大三位数最小三位数（2）能被3整除的的最大三位数最小三位数（3）能被5整除的的最大三位数最小三位数（4）能同时被2、5整除的的最大三位数最小三位数【例4】【基础】从0，1，3，5四个数中选出一个，组成三位数能同时被2、3、5整除的数的个数是（）个A.1个B. 2个C. 3个D. 4个【提高】要使六位数□3478□能被15整除，□内应分别填上几？写出这些数.【尖子】一个两位数是偶数，被3除余1，被5除余3，求满足条件的最大的两位数【例5】【基础】四个连续偶数的和是164，求夹在这四个偶数之间的奇数是什么？【提高】有一个四位数是能被5整除的偶数，它的前两位是能被3整除的最小的两位数，四位数字之和是奇数，则这个四位数可能是什么？【尖子】99个连续的自然数的和是奇数，还是偶数？小华和小强在回答这个问题时发生了分歧，小华说是奇数，小强说是偶数，请你评一评，谁说的对?因数、倍数五、因数、倍数（1）如果a能被b整除，那么a叫b的倍数，b叫a的因数.（2）一个数的因数的个数是有限的，最小的是1，最大的是本身；（3）一个数的倍数的个数是无限的，最小的是本身（即一个数：最大因数．．．．=本身．．★）．．．．=最小倍数【例6】【基础】已知117÷9=13，根据此式，判断下列说法中，错误的是（）A. 117是9的倍数B. 9是117的因数C. 13是117的因数D. 117是倍数，9、13是因数【提高】下列说法错误的有（）①30÷4=7.5，所以30是4和7.5的倍数②9.1÷1.3=7，所以9.1是1.3的倍数③1是所有正整数的因数④8的倍数中，最小的是一个是16⑤一个数既是16的倍数，也是16的因数，那么这个数是16A. 2个B. 3个C. 4个D. 5个【尖子】（1）一个数的最小倍数是32，它的因数有__________个，分别是____________________（2）一个数最小倍数和最小因数相差24，这个数的所有因数是___________________【例7】【基础】一个数的最大因数是27，这个数还有（）个因数A. 2B. 3C. 4D. 无数个【提高】a、b、c是三个不同的正整数，根据a÷b=c，a的因数至少有（）个A. 2B. 4C. 6D. 无数个【尖子】已知A=2×3×5，B=3×3×5，则A和B相同的因数是___________【例8】把64个球装在盒子里，每个盒子装得同样多，则好装完（1）有几种装法？（列出算式）（2）如果有67个球呢？【例9】辅导员带领24名学生参加夏令营，为了便于活动，将这24名学生分成若干个人数相等的小组，要求每个小组人数不少于5人，应当如何分组呢？素数、合数六、素数、合数（1）素数：除了1和本身，没有其他因数的正整数叫素数。