下载文档原格式
差错控制编码基本原理
以下是差错控制编码的基本原理：
1.编码器：编码器是负责添加冗余码的模块。
它将待发送的数据分割成块，并根据特定的编码规则生成冗余码。
常用的差错控制编码技术包括奇偶校验、循环冗余检验码（CRC）、海明码等。
2.冗余码：冗余码是编码器生成的额外信息，用于检测和纠正差错。
冗余码通常通过对数据进行其中一种计算生成，能提供额外的冗余信息以便于差错检测和纠正。
不同的冗余码具有不同的性能特点，如比特错误检测能力、纠正能力等。
3.传输：编码器将原始数据和冗余码一同发送给接收方。
传输介质可能会引入噪声、干扰和差错，可能会导致数据发生变化。
4.解码器：解码器负责接收和解码接收到的数据。
它使用相同的编码规则对接收到的数据进行解码，并生成相应的冗余码。
5.比较和校验：解码器将解码后的数据和接收到的冗余码进行比较和校验。
如果冗余码与接收到的数据一致，说明数据未发生错误。
否则，说明数据发生了差错。
6.纠错：当解码器检测到差错时，纠错算法会尝试恢复或修正接收到的数据。
纠错的能力取决于所使用的具体差错控制编码技术。
一般来说，能够检测到错误的位数并进行纠正的编码技术能够提供更好的纠错能力。
总结来说，差错控制编码通过添加冗余码在传输数据时提供了差错检测和纠正的能力。
它的基本原理是在发送方使用编码器对数据进行编码，添加冗余码；接收方使用解码器对接收到的数据进行解码，并进行差错检
测和纠正。
不同的差错控制编码技术具有不同的特点，可根据实际需求选择合适的编码技术来提高数据传输的可靠性。
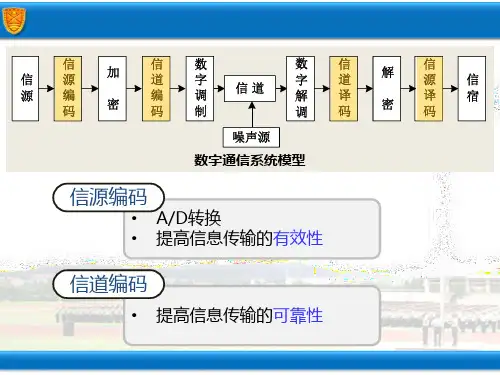
2.差错控制编码2.1. 引言什么是差错控制编码（纠错编码、信道编码）？为什么要引入差错控制编码？差错控制编码的3种方式？本章主要讲述：前向纠错编码（FEC）、常用的简单编码、线性分组码（汉明码、循环码）、简单介绍RS码*、BCH码*、FIRE码*、交织码，卷积码极其译码、TCM编码*。
一、什么是差错控制编码及为什么引入差错控制编码？在实际信道上传输数字信号时，由于信道传输特性不理想及加性噪声的影响，接收端所收到的数字信号不可避免地会发生错误。
为了在已知信噪比情况下达到一定的误比特率指标，首先应该合理设计基带信号，选择调制解调方式，采用时域、频域均衡，使误比特率尽可能降低。
但若误比特率仍不能满足要求，则必须采用信道编码（即差错控制编码），将误比特率进一步降低，以满足系统指标要求。
随着差错控制编码理论的完善和数字电路技术的发展，信道编码已经成功地应用于各种通信系统中，并且在计算机、磁记录与存储中也得到日益广泛的应用。
差错控制编码的基本思路：在发送端将被传输的信息附上一些监督码元，这些多余的码元与信息码元之间以某种确定的规则相互关联（约束）。
接收端按照既定的规则校验信息码元与监督码元之间的关系，一旦传输发生差错，则信息码元与监督码元的关系就受到破坏，从而接收端可以发现错误乃至纠正错误。
研究各种编码和译码方法是差错控制编码所要解决的问题。
二、差错控制的三种方式1、检错重发（ARQ）检错重发：在接收端根据编码规则进行检查，如果发现规则被破坏，则通过反向信道要求发送端重新发送，直到接收端检查无误为止。
ARQ系统具有各种不同的重发机制：如可以停发等候重发、X.25协议的滑动窗口选择重发等。
ARQ系统需要反馈信道，效率较低，但是能达到很好的性能。
2、前向纠错前向纠错（FEC）：发送端发送能纠正错误的编码，在接收端根据接收到的码和编码规则，能自动纠正传输中的错误。
不需要反馈信道，实时性好，但是随着纠错能力的提高，编译码设备复杂。
差错控制编码的基本原理你想啊，在咱们这个信息的世界里，数据就像一个个调皮的小精灵，到处跑来跑去。
可是呢，在传输的过程中，这些小精灵可能就会迷路或者出岔子，就像你给朋友传个小纸条，路上被风吹破了一角啥的。
这时候差错控制编码就像一个超级保镖闪亮登场啦。
差错控制编码呢，其实就是给这些信息小精灵穿上一层特殊的保护衣。
比如说咱们有原始的信息，就像你要送出去的精美小礼物。
这个原始信息可能是一串简单的数字或者字母啥的。
但是直接就这么送出去，它很脆弱的哦。
于是呢，咱们就根据一定的规则，给这个原始信息加上一些额外的东西，这就像是给小礼物包上一层又一层的漂亮包装纸。
这些额外加的东西可不是随便加的，是按照特定的算法来的呢。
打个比方哈，假如咱们的原始信息是“101”，通过差错控制编码的规则，可能就变成了“101110”。
这里面后面的“110”就是咱们给原始信息加上的保护部分。
为啥要这么加呢？这就涉及到它的神奇之处啦。
当这个加了保护衣的信息在传输过程中遇到了干扰，比如说被雷劈了一下信号（当然这是夸张啦），某个数字可能就变了。
如果没有差错控制编码，那接收方收到错误的信息就蒙圈了，根本不知道是啥。
但是有了这个编码就不一样啦。
接收方知道这个编码的规则呀，它就可以根据收到的信息，去检查有没有错误。
就像你朋友收到那个被风吹破一角的纸条，但是因为你之前和他有个小暗号（就像差错控制编码的规则），他就能大概猜出纸条上原来完整的内容。
而且差错控制编码还有不同的类型呢。
有一类叫检错码，这个就像是一个小侦探。
它能发现信息在传输过程中有没有出错，但是它不知道具体哪里错了。
就像你发现小礼物的包装纸破了个洞，你知道有问题，但还不清楚里面的礼物到底坏没坏。
还有一类叫纠错码，这个就更厉害啦，它不但能发现错误，还能把错误给纠正过来。
这就好比你朋友收到纸条，发现有个地方模糊不清，但是根据你们的暗号，他能准确地把模糊的字给还原出来。
在实际的通信系统里，差错控制编码可重要啦。
1．垂直奇偶校验码： 编码原理：
（1）将整个发送的数据块分为定长为m 的n 个组，一般m 为字符位数或位数的倍数，一组称为一个码字。
（2）每组末位按“1”的个数位奇数或者偶数的规律加一个
校验位j
r （
n j ,3,2,1=）
，使得每组包括校验位在内“1”的个数为奇数或偶数。
为偶数的称为偶校验，为奇数的称为奇校
验。
（ij
b 为一个比特位，运算为二进制运算）
校验位计算为： 偶校验 mj j j j b b b r +++= 21n
j ,3,2,1= 奇校验
121++++=mj j j j b b b r n
j ,3,2,1=
举例说明：
每一列代表一个码字：
1
011111001101
偶校验计算的校验位为：0111 奇校验计算的校验位为：1000
校验能力：只能检测每列码字中的奇数个错误，所有偶数个错误全部漏检。
实现方法：用硬件和软件均可，可以边发送边产生冗余位，接收时可以边接收边去掉冗余位。
2．水平奇偶校验码 编码原理：
（1）将整个发送的数据块分为定长为m 的n 个组，一般m 为字符位数或位数的倍数，一组称为一个码字。
（2）将n 个码字排成一个矩阵，对各个码字相应横向位进行奇偶校验。
（校验位的生成与垂直奇偶校验码生成方式一致）。
偶校验 in i i i b b b r +++= 21m i ,3,2,1= 奇校验 121++++=in i i i b b b r m i ,3,2,1=
（3）发送时将所有码字发送完后发送校验位。
举例说明： 奇 偶
每一列代表一个码字：
1
011111001101
01
0 1
10
1
校验能力：可以检测各个码字同一位上的奇数位错，对于长度小于或等于m 的突发错误，由于分布在不同行中，可以检测到。
实现方式：用硬件和软件均可，需要借助存储器。
3．水平垂直奇偶校验
编码原理：同时进行垂直和奇偶校验。
（过程略）
校验能力：冗余度大，具有更强检错能力。
可检验3位以下的全部错误，所有奇数位错，突发长度小于或等于m+1的突发错误以及绝大多数偶数位错。
4、斜奇偶校验
编码原理：在水平垂直奇偶校验码的基础上，按照斜对角线的方向计算出校验位。
校验能力：冗余位更多，编、译码较为复杂，校验能力更强。
正反码：
举例说明：
码长n＝10，信息位k＝5，校验位r＝5，若信息位为11001，校验位为11001，码字为1100111001；若信息位为10001，校验位为01110，码字为1000101110。
纠错规则：
若发送码字1100111001，
接收码字1100111001（传输中无错），
合成码为11001＋11001＝00000，
接收码信息位有3个1，校验码为00000。
据上表，没有发生错误。
接收码字1000111001
合成码为10001＋11001＝01000，
接收码信息位有偶数个1，校验码为合成码的反码10111，据上表，信息位第二位出错。
（同学自己举例说明其他情况）。
循环冗余校验码 1、码多项式
如果把一个码字中的各位看作是一个多项式的系数，则长为n 的码字)(0121c c c c C n n --=可以表示为一个多项式：
1
2
2
1
1
)(c x c x c x c x C n n n n ++++=----
该多项式称为码字的码多项式。
如：码字11001的码多项式为：
110011)(3
4
1
2
3
4
++=⋅+⋅+⋅+⋅+⋅=x x
x x x x x C
2、多项式的按模运算
在CRC 中，常需要进行码多项式的运算，运算规则为按模2运算。
若任意的n 次多项式)(x T 被一个k 次多项式)(x k 除，得到商式)(x Q 和余式)(x R （次数必然小余k ），则表示为
)()()()(x R x Q x k x T +=。
3、循环冗余码
长为n 的码，信息位为k 位的码记为（n ，k ）码。
若一个码字集合满足以下两个条件：
（1）循环性：码集中的任一个码字向左或右循环一位，得到的新的码字，仍为码集中的码字。
（2）封闭性：码集中任意两个码字之和仍为码集中的码字。
则称此码集为（n ，k ）循环码。
例：)(0121c c c c C n n --=是码集中的码字，)(1210c c c c C n -=是码集中的码字，全零码字必然是码集中的码字。
4、循环冗余码的生成多项式
定理1 在循环冗余码（n ，k ）中，存在且只有一个（n －k ）次的码多项式
1
2
2
2
2
)(g x g x g x g x x G k n k n k
n +++++=-----
满足：
（1）此循环冗余码中任一多项式都是)(x G 的倍式；
（2）任意一个（n －1）次或（n －1）次以下的，又是)(x G 倍
式的多项式必定是此循环码中的一个码多项式。
（生成多项式的寻找有严密的代数背景，略） 5、循环冗余码的编码
一般是已知信息位，根据信息位求冗余位。
信息位为)(0121c c c c K k k --=，码多项式为
1
2
2
1
1
)(c x c x c x c x K k k k k ++++=----
冗余位为)
(021r r r R k n k n ----=，码多项式为
012
21
1)(r x r x
r x
r x R k n k k n k n ++++=-------
码字为)(0210121r r r c c c c T
k n k n k k ------=，码多项式为
)()()(x R x K x x T k n +=- （1）
码字是生成多项式)(x G 的倍式，则
)()()(x Q x G x T = （2） 由（1）（2）两式得
)()(x R x K x k n +-＝)()(x Q x G
即 )(x K x k n -＝)()()(x R x Q x G +
所以用)(x K x k n -去除以生成多项式)(x G 得到的余式就是码字的校验位。
编码算法：
（1）用k n x -乘以信息位对应的码多项式)(x K ；
（2）用生成多项式)(x G 去除)(x K x k n -，得余式)(x R ； （3）将)(x R 对应的码字加在信息位后发送即可。
6、循环冗余码的译码 （1）检错过程
发送方发送码字)(x T ，设接收方接收码字为)('x T ，根据
)()()(x Q x G x T =
若)('x T ＝)(x T ，则有
)()()('
x Q x G x T =
即)('x T 除以)(x G 没有余式。
若)('x T <>)(x T ，则)('x T 除以)(x G 有余式，接过收到的码字
出错。
据此译码过程可知出现错误。
注意：有时)('x T <>)(x T ，)('x T 除以)(x G 也没有余式，这种情况说明错误超过该编码的检错能力，每一种码的检错能力与生成多项式选择有关。
（2）纠错过程
对于每一种编码，由其生成多项式可得到码的检错能力在某一个范围内，即该码可检m 位错，纠s 位错。
在这个范围内可得到一个特定的错误模式，当余式)(x R 与这些错误模式存在一一对应关系时，便可以纠错。
