第8章 广义单自由度体系-23
- 格式:ppt
- 大小:1.84 MB
- 文档页数:5


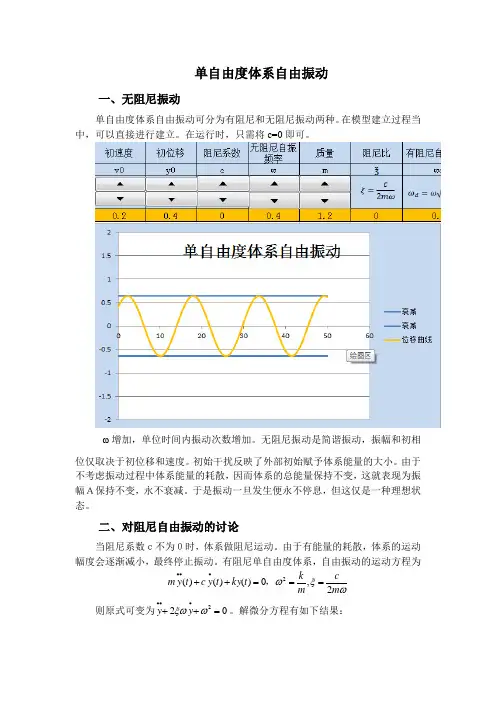
单自由度体系自由振动一、无阻尼振动单自由度体系自由振动可分为有阻尼和无阻尼振动两种。
在模型建立过程当中,可以直接进行建立。
在运行时,只需将c=0即可。
ω增加,单位时间内振动次数增加。
无阻尼振动是简谐振动,振幅和初相位仅取决于初位移和速度。
初始干扰反映了外部初始赋予体系能量的大小。
由于不考虑振动过程中体系能量的耗散,因而体系的总能量保持不变,这就表现为振幅A保持不变,永不衰减。
于是振动一旦发生便永不停息,但这仅是一种理想状态。
二、对阻尼自由振动的讨论当阻尼系数c不为0时,体系做阻尼运动。
由于有能量的耗散,体系的运动幅度会逐渐减小,最终停止振动。
有阻尼单自由度体系,自由振动的运动方程为ωξωm c m k t ky t y c t y m 2,0)()()(2===++∙∙∙, 则原式可变为022=++∙∙∙ωξωy y 。
解微分方程有如下结果:2.1 当1<ξ时,即小阻尼运动,方程的解为:)sin(A )sin cos ()(000ϕωωωξωωξωξω+=++=--t e t y v t y e t y d t d d d t 其中2200201)(ξωωωξω-=++=d d y v y A可画出小阻尼体系自由振动时的y-t曲线如图所示:是一条逐渐衰减的波动曲线2.2 当1>ξ时,即大阻尼的情况,方程的解为:⎥⎥⎦⎤⎢⎢⎣⎡-+--+=-t ch y t sh v y e t y o t ωξωξξξωωξ11)1()(20220 上式不含有简谐振动的因子,是因为体系受干扰后偏离平衡位置所积蓄起来的初始能量在恢复平衡位置的过程中全部消耗克服阻尼,由于阻尼很大,不足以引起振动。
当初始速度,初始位移都大于0时,可画出大阻尼体系自由振动时的y-t曲线如图所示:2.3 当1=ξ时,即临界阻尼的情况,方程的解为:[]t v t y e t y t 00)1)(++=-ωω(当初始速度,初始位移都大于0时,可画出临界阻尼体系自由振动时的y-t曲线如下图所示;当体系在临界阻尼时,其运动衰减的最快,即他能在最短时间内无振动的回到平衡位置。



单自由度系统模态计算一、引言单自由度系统是结构动力学中一个重要的研究对象,它可以用来描述许多实际工程中的振动问题。
在计算单自由度系统的模态时,我们需要了解什么是模态、模态计算的目的以及常用的计算方法。
二、什么是模态模态是指一个振动系统在固有频率下的振动形态。
对于单自由度系统来说,它的振动主要由一个自由度(通常是一个质点的位移)决定,而模态则是描述这个振动的特征。
每个模态都有一个固有频率和振型。
三、模态计算的目的模态计算的目的是确定单自由度系统的固有频率和振型。
固有频率是系统在没有外力作用下自由振动时的频率,而振型则是系统在该频率下的振动形态。
通过模态计算,可以帮助我们了解系统的振动特性,进而进行动力设计和振动控制。
四、常用的模态计算方法常见的模态计算方法包括解析法和数值计算法。
解析法主要是通过对系统的微分方程进行求解,得到固有频率和振型的解析解。
数值计算法则是利用计算机进行数值模拟,通过数值求解的方法来计算固有频率和振型。
1. 解析法解析法主要有两种常见的方法,即初始条件法和特征值法。
初始条件法是通过给定初始条件,求解系统的微分方程,得到固有频率和振型的解析解。
特征值法则是将系统的微分方程转化为特征值问题,通过求解特征值和特征向量来得到固有频率和振型。
2. 数值计算法数值计算法主要包括有限元法和模态超级位置法。
有限元法是一种常用的工程计算方法,通过将系统离散化为有限个子结构,然后求解子结构的固有频率和振型,最后组合得到整个系统的固有频率和振型。
模态超级位置法则是通过对系统的响应进行频谱分析,得到系统的固有频率和振型。
五、总结通过模态计算,我们可以了解单自由度系统的固有频率和振型,从而更好地理解和分析系统的振动特性。
在实际工程中,模态计算是进行结构动力学分析和振动控制的重要手段。
不同的计算方法可以根据具体情况选择,以获得准确和可靠的结果。
因此,掌握单自由度系统模态计算的方法和原理是非常重要的。
通过本文的介绍,希望读者对单自由度系统模态计算有一个初步的了解,并能够在实际工程中灵活应用。



“结构力学I”课程标准课程名称:结构力学I英文名称:Structural Mechanics I课程代码:课程类别:专业教育必修课程(专业核心课程)课程学时:56课程学分:3.5适用专业:土木工程先修课程:高等数学、理论力学、材料力学等授课学院:建筑工程学院教研室:土木工程教研室制定人:赵腾飞、袁立群、孟昭博审定人:张绪涛、孟昭博、崔诗才一、课程性质《结构力学I》是土木工程专业必修的专业核心课程之一,将为后续专业课程学习打下良好的基础。
通过本课程的学习,学生在理论力学和材料力学的基础上可以进一步掌握分析计算杆件体系的基本原理和方法,了解各类结构的受力性能,培养学生结构分析与计算的能力,为学习有关专业课程及进行结构设计和科学研究打下基础,并能够应用结构力学基本理论和方法解决工程实际问题。
二、目标要求(一)总体目标掌握结构在荷载、支座移动等因素作用下结构强度、刚度等的分析、计算方法;掌握结构的合理组成形式及分析方法;熟悉结构力学相关的基本概念,了解近似计算方法、了解计算结构力学的相关分析方法。
在头脑中初步建立结构的力学思维方式,能正确应用力学知识对结构的强度、刚度以及结构合理组成进行分析。
(二)具体目标1.知识目标(1)能理解结构力学的一般概念及结构受力、变形等特点;(2)能正确建立力学相关计算模型并对其进行结构几何组成分析;(3)能正确利用多种方法对结构进行受力分析、绘制相应的内力图;(4)能正确通过虚功法求解结构的位移,并能大致绘制结构的变形图。
2.能力目标(1)能熟练计算、绘制静定结构、超静定结构的内力;(2)能熟练求出指定截面的广义位移;(3)能判别平面杆系结构的几何组成合理性。
3.素质目标(1)能将力学知识应用于实际工程中,着力培养工程实践能力;(2)引入前延、后续课程,做好课程衔接,形成课程体系,为后学专业课学习打好基础;(3)培养学生的受力概念、直观受力感觉和力学意识,勇于担当结构安全和经济两大重任。


单自由体系名词解释
单自由度系统(Single Degree of Freedom System)是指工程动力学和振动学中常用的一个概念,用来描述一个仅有一个自由度运动的系统。
这个自由度通常是指系统的一个独立运动参数,如质点在一维空间内的位移或者转角。
在单自由度系统中,该自由度的运动可以完全描述整个系统的动态特性。
单自由度系统的经典例子是弹簧质点振子系统,也就是简谐振动系统。
这种系统由一个质点 (质量为m)通过一根弹簧 (弹性系数为k)与一个固定支点相连构成。
该质点在弹簧的作用下可以在水平方向上作简谐振动。
单自由度系统的重要特征包括:
- 自由度: 单自由度系统中仅有一个运动自由度。
- 动力学方程: 可以使用牛顿运动定律和哈克定律等原理来建立该系统的运动方程,描述质点运动的规律。
- 简谐振动: 如果系统的回复力服从胡克定律,并且没有阻尼和外力的作用,系统将表现出理想的简谐振动。
- 阻尼和非线性: 通常情况下,单自由度系统可能会有阻尼和非线性因素的存在,这会使得其振动特性发生变化。
单自由度系统的研究对于理解振动学原理、分析结构动力学响应、设计工程结构等方面都具有重要意义。
它为工程师和研究人员提供了一种简化模型来分析和预测结构或系统的振动行为,对于许多工程应用和设计过程都具有指导意义。
1/ 1。
一、概述单自由度体系是指系统中只有一个可以自由运动的质点,它的运动可以由一个广义坐标来描述。
对于单自由度体系,可以采用杜哈姆积分的方法求解系统的运动方程,并绘制出对应的时程曲线。
本文将对单自由度体系的杜哈姆积分与时程曲线进行探讨。
二、杜哈姆积分的基本原理杜哈姆积分是一种对变阻尼振动系统非定常响应的数值积分方法。
对于线性系统,杜哈姆积分可以简化为一个积分型的微分方程,其基本原理可以用以下公式表示:其中,x(t)为系统的位移,x0表示系统的初始位移,v(t)为位移的导数,ω为系统的固有频率,t为时间,F(t)为外力。
利用杜哈姆积分方法,可以求解系统在给定外力作用下的位移和速度。
三、杜哈姆积分的应用杜哈姆积分广泛应用于工程实践中,尤其是在机械振动、结构动力学和地震工程中。
在求解单自由度体系的非定常响应时,我们可以利用杜哈姆积分方法得到系统的位移和速度随时间的变化规律。
四、时程曲线的绘制通过杜哈姆积分方法求解得到系统的位移和速度随时间的变化规律后,我们可以利用这些数据绘制出对应的时程曲线。
时程曲线可以直观地展示系统在外力作用下的振动情况,有利于工程师对系统的动态响应进行分析和评估。
五、实例分析以弹簧振子为例,假设有一个质量为m的弹簧振子,弹簧的刚度为k,外力为F(t),系统的初始位移和初始速度分别为x0和v0。
利用杜哈姆积分方法,我们可以得到弹簧振子在外力作用下的位移和速度随时间的变化规律,并绘制出对应的时程曲线。
六、结论杜哈姆积分方法是一种对变阻尼振动系统非定常响应进行数值积分的有效方法。
通过对单自由度体系的杜哈姆积分和时程曲线的分析,我们可以更好地理解系统在外力作用下的动态响应规律,并为工程实践提供重要参考。
七、展望未来,我们可以进一步研究杜哈姆积分方法在多自由度体系和非线性系统中的应用,探索更加精确和高效的变阻尼振动系统响应预测方法,为工程实践和科研工作提供更加可靠的理论基础和技术支持。
单自由度体系的杜哈姆积分与时程曲线是工程动力学研究中的重要内容,它对于理解和预测系统动态响应具有重要意义。
单自由度体系结构我身边站着一位老者,他眯着眼,手轻轻搭在桥的栏杆上,那栏杆被岁月侵蚀得有些斑驳了。
“你看这桥啊,”老者缓缓开口,声音带着一种历经沧桑后的平静,“就这么晃悠着,却稳稳当当这么多年。
”我好奇地看着他,问道:“大爷,您这话怎么说呢?”老者笑了笑,指了指脚下的桥板。
“这桥啊,就像一个只能在一个方向上自由活动的东西,就好比你只能前后晃动一个小玩偶一样,这就是单自由度。
”我有点似懂非懂,挠了挠头。
这时候,旁边一个年轻人凑了过来,笑着说:“大爷,您可真会比喻。
那这单自由度有啥特别的呢?”老者站直了身子,眼睛里闪过一丝光亮。
“嘿,这特别之处可多咯。
你想啊,这桥要是这儿动一下,那儿动一下,没有个规律,那不早就散架啦?单自由度呢,就像给它定了个规矩,只能按照一种方式去动。
”我们三个人站在桥上,感受着微风拂过。
我低头看着桥下的溪水,脑海里努力理解着老者的话。
突然,我想到了秋千。
“大爷,那秋千是不是也是单自由度体系结构啊?”老者赞许地点点头。
“对喽,小娃娃很聪明嘛。
你看秋千,就只能前后荡,这就是一个自由度。
它的结构决定了它只能这么运动。
”年轻人似乎也来了兴趣,他走到桥的另一头,又走回来,边走边说:“那这种单自由度体系结构在建筑里很常见吗?”老者摸了摸下巴。
“常见得很呢。
就像那些简易的棚子,屋顶如果只考虑上下晃动(当然我们不希望它晃啦),那也是单自由度的体现。
”我心里默默想着,原来生活中有这么多单自由度体系结构的例子啊。
这时候,一只小鸟飞了过来,停在了桥栏上,叽叽喳喳叫着,仿佛也在参与我们的讨论。
老者看着小鸟,笑着说:“你们再看这小鸟,它虽然能飞来飞去,但是如果把它放在一个小笼子里,只能上下跳动的时候,那这个小空间对于小鸟来说就像是一个单自由度体系。
”年轻人听了,哈哈大笑起来。
“大爷,您这联想可真丰富。
不过这样一对比,好像还真挺形象的。
”我也跟着笑了,感觉对单自由度体系结构的理解更深刻了。
从这座桥上离开的时候,我回头看了看。