第二节单自由度体系的运动方程

格式：ppt
大小：290.50 KB
文档页数：11

下载文档原格式

第二节单自由度体系的运动方程

m y ( t ) c y ( t ) k y ( t ) P ( t ) 11
式表明，若建立体系的运动方程时以静平衡位置作为计算位移的起点，则所得动位移的微分方程与重力无关。以后在建立体系的运动方程时，将不标出重力W及其产生的静位移 st 。上述方法是直接利用达朗贝尔原理建立质点m在任一瞬时的动力平衡方程，它要用到结构的刚度系数k11，所以又称为刚度法。

3 11 l l l 2 l ) 1 P ( EI 2 22 4 EI
运动方程为
EI 1 y ( t ) 3y ( t ) P ( t ) ml 4 m
图 ) R ( t ) P ( t ) 11
即
1 m y ( t ) c y ( t ) y ( t ) P ( t )

11
式中 11 为柔度系数，它表示在质点上沿质点运动方向施加单位力引起质点沿运动方向的静位移。柔度系数与刚度系数k11互为倒数.由于建立运动方程要用到体系的柔度系数，所以又称为柔度法。
一、列动力平衡方程(刚度法) 利用平衡条件建立运动方程
图11-10
在振动的任一时刻t取质点m为隔离体作用在质点上的力有(各力以指向y(t)的正方向为正)： (1)重力W。 (2)动力荷载P(t)。
图11-10
(3)弹性恢复力 S(t)。它是由于杆件的弹性变形而施加于质点的力，它的大小与质点的位移成正比，但方向相反，即
§11-2 单自由度体系的运动方程
• 动力计算的基本未知量是质点的位移，它是时间t的函数。为
了求出动力反应，应先列出求解质点位移的方程。描述体系振动时质点动位移的数学方程，称为体系的运动方程(或振动方程)。

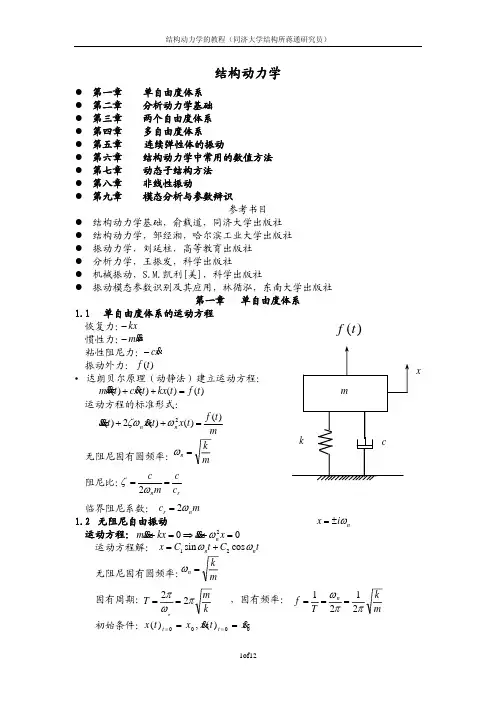
动力学(第1章)

f
(t)
=
2P0
ωt π
∫ ∫ bi
=
2 T
T 0
f (t) sin(iωt)dt = 4ω π
π 2ω 0
f
(t) sin(iωt)dt
=
8P0 i2π 2
i −1
(−1) 2 (i
= 1,3,5,⋅⋅⋅)
6of12
结构动力学的教程（同济大学结构所蒋通研究员）
∑ 取
i=1~3
β1 算得：
=
1
−
1 ω2
= 1−ω
2ζω 3 2 + (2ζω )2
1+ 4ζ 2ω 2 (1− ω 2 )2 + (2ζω )2
5of12
结构动力学的教程（同济大学结构所蒋通研究员）
隔振要求：频率比： ω
=
ω
>
2⇒
ωn
阻尼比小：ζ ↓⇒ A ↓
B
A <1 B
但过小通过共振区不利
主动隔振：将振源隔开，使振动传播不出去（隔振器）
+ϕ)
振幅与相位角： A=
x02
+
⎜⎜⎝⎛
x&0 ωn
⎟⎟⎠⎞2
,ϕ
=
arctg
ωn x0 x&0
x
A
x&0
x0
t ϕ /ωn
t t +T
例题 1-1 求图示体系的固有频率
悬臂梁刚度：k1
=
3EI l3
与 K2 并联后等效刚度：k = k1 + k2 固有频率:ωn = k / m （串联弹簧）
l m
• •
能量守衡：We +Wd + Wf = 0 → ω = ωn →

结构力学-单自由度体系的自由振动

mh3 T 2 24 EI
Vibration Characteristic
y(t ) Asin( t )
Acceleration： Inertia Force：
(t ) A 2 sin(t ) y (t ) mA 2 sin(t ) I (t ) m y
这是一个齐次方程，其通解为
y(t ) C1 cost C2 sin t
C1 和 C2 可由初始条件确定，设初始位移和初始速度分别为
y(0) y0 C1 y0
(0) v0 y
C2
v0
v0

,
y (t ) y0 cos t

sin t
y (t ) y0 cos t
在无阻尼自由振动中，位移、加速度和惯性力都按正弦规律
变化，且作相位相同的同步运动，即它们在同一时刻均达极值，
而且惯性力的方向与位移的方向一致。
幅值产生于
sin(t ) 1 时，其值分别为：
y A
A 2 y
I mA

2
由于在运动的任一瞬时质体都处于平衡状态，在幅值出现时
l

1 m
EA ml
st Wl T 2 2 g EAg
例: 求图示结构自振频率。（EI 为常数，杆件自身质量不计） [分析] 图乘法求位移
A m C l h
1 1 2 2 1 2 h2 B ( h h hl h) (h l ) EI 2 3 2 3 3EI
y y

v0

sin t
T
0
t
y cos t
-y
y

12.2单自由度体系的运动方程

(
&& + k B b 2α = 0 m1 a + m2 l α
2 2
)
All Rights Reserved
重庆大学土木工程学院®
【例12-3】试用柔度法建立图】试用柔度法建立图12-14a所示静定刚架受动力荷载所示静定刚架受动力荷载作用的运动方程。作用的运动方程。 M (t) M (t)
重庆大学土木工程学院®
All Rights Reserved
3EI 1 m&& + 3 y = M ( t ) y 2l 4l
l
m
y
M( EI B
C
EI A
也可写作
m&& + k11 y = FE (t ) y
为等效动力荷载
l
FE (t )
FE (t ) = (δ1P δ11)M(t )
&& FI1 = −m1 (aα ) &&) FI 2 = −m2 (lα
FB = k B (bα )
All Rights Reserved 重庆大学土木工程学院®
解：由∑MA＝0，得，整理后，整理后，得运动方程
&& && m1 a 2α + m2 l 2α + k B b 2α = 0
y = δ11 FI + δ11 FC + δ11 FP ( t )
All Rights Reserved 重庆大学土木工程学院®
(12-6)
y = δ11 FI + δ11 FC + δ11 FP ( t )
(12-6)

结构动力学 -单自由度体系的振动

负号表示等效力的方向和地面加速度方向相反。
13
§2.2 无阻尼自由振动
自由振动(free vibration) ：无外界干扰的体系振动形态称为自由振动（free vibration）。振动是由初始位移或初始速度或两者共同影响下所引起的。无阻尼自由振动：如果阻尼系数等于零，则这种自由振动称为无阻尼自由振动（undamped free vibration）。假设由于外界干扰，质点离开平衡位置，干扰消失后，质点将围绕静力平衡点作自由振动。
或：m y ( t) c y ( t) k ( t) y m y g ( t) P e( f t) f
Peff (t ) ：等效荷载，即在地面加速度yg (t )影响下，结构的响
应就和在外荷载p (t )作用下的响应一样，只是外荷载 p (t )
等于质量和地面加速度的乘积。
干扰力的大小只能影响振幅A的大小，而对结构自
振周期T的大小没影响。
（2）自振周期与质量平方根成正比，质量越大，则
周期越大；自振周期与刚度的平方根成反比，刚度
越大，则周期越小。要改变结构的自振周期，只有
改变结构的质量或刚度。
24
§2.2 无阻尼自由振动
k g
m
st
（3）把集中质点放在结构上产生最大位移的地方，则可
1、位移以静力平衡位置作为基准的，而这样确定的位移即为动力响应。
2、在求总挠度和总应力时，要把动力分析的结果与静
力分析结果相加。
9
§2.1运动方程的建立
3、支座运动的影响结构的动位移和动应力既可以由动荷载引起，也
可以由结构支座的运动而产生。 1）由地震引起建筑物基础的运动； 2）由建筑物的振动而引起安置在建筑物内的设备基底的运动等等。

201单自由度体系运动方程(力学)

yst yd
k
静平衡位置
c
m m
注意：质点的位移、速度和加速度以向下为正。
k m
c
k m
c
yst
k m
c
yst
y = yst + yd
yd
y y , y ,
静平衡位置
FP(t)
y y st yd y yd d y y
位
移
displacement
速度
velocity
讨论：同一体系，激励位置不同，质量m的运动方程是否相同？
m m
FP(t)) 11 FI ( t ) FS ( t ) 1P FP ( t )
1P mu ku FP ( t ) 11
1P FE ( t ) FP ( t ) 11
1. 建立体系运动方程方法
为什么要研究单自由度体系？ 1. 许多动力问题常可按单自由度体系进行计算或进行初步估算 2. 单自由度体系的分析是多自由度体系分析的基础 3. 许多概念由单自由度分析引出
单自由度体系运动方程的一般形式：
m k 水平运动模型 k m
m m
k
竖向运动模型
2. 刚度法（列动力平衡方程）
m cy y
1

y FP ( t )
1 k
与刚度法推出的运动方程相比较可见
4. 虚功法（对于刚体系特别方便）
δy k
FI y FD y FS y FP y 0
FP(t)
c
FI FD FS FP y 0
FI FD FS FP 0
加速度 acceleration

单自由度体系的自由振动

令
ω2 = k
m
y + ω 2 y = 0
运动方程的解 y + ω 2 y = 0 可由振动的初 2
始条件来确定
常系数的线性齐次微分方程，其通解为
y(t) = A1 cosωt + A2 sinωt
若当 t = 0 时 y = y0 初位移
y(0) = y0 = A1 cosω × 0 + A2 sin ω × 0
因此，自振周期（或频率）的计算十分重要。
例计算自振频率
14
EI=常数
如果让振动体系沿振动方向发生单位位移时，所有刚结点都不能发生转动（如横梁刚度为无穷大的刚架) 计算刚度系数方便。
两端刚结的杆的侧移刚度为：12EI
l3
一端铰结的杆的侧移刚度为：3EI
l3
例计算自振频率
1
k11
EI=常数
12 EI l3
y = y0 初速度
y(0) = y0 = −ωA1 sinω × 0 + ωA2 cosω × 0
A1 = y0
A2
=
y0
ω
y(t)
=
y0
cosωt
+
y0
ω
sin ωt
位移的多项表达式
位移、速度的单项表达式
3
y(t)
=
y0
cosωt
+
y0
ω
sin ωt
若令
y(t) = a sinϕ cosωt + a cosϕ sin ωt
结构自振周期、频率
6
自振周期的倒数称为工程频率 f = 1
（或频率），记作 f
T
频率 f 表示单位时间内的振动次数，其常用单位

2-1结构动力学(单自由度)

c 2 m
O
t
这条曲线仍具有衰减性，但不具有波动性。
1, cr 2m
c 2m
c cr
阻尼比
（2）ξ> 1（强阻尼）情况
1,2 2 1 0
y t C1e1t C2e2t
t

y( t )
O
y (t ) e t C1 sinh 2 1 t C 2 cosh 2 1 t
g y st
y st m T 2 2 k g
频率只取决于体系的质量和刚度，而与外界因素无关，是体系本身固有的属性，所以又称为固有频率
（natural frequency）。
（3）简谐自由振动的特性
y(t ) Asin( t )
(t ) A 2 sin(t ) y 加速度为：惯性力为： FI (t ) m (t ) mA 2 sin(t ) y
特征根一般解
2 2 2 0
1, 2 2 1

y(t ) C1e
1t
C2 e
2t
（1）ξ= 1（临界阻尼）情况
1,2
y C1 C2 t e t
y( t )
tan v

t
y y0 (1 t ) v0t e
d
阻尼对自振频率、周期的影响
,
d
Td T
在工程结构问题中，若0.01<ξ<0.1，可近似取:
d , Td T
y(t ) e t Asin ( d t )
阻尼对振幅的影响
yk Aetk Td e y k 1 Ae (tk Td )

《结构力学》结构动力学(2)

为最大的动力位移与静力位移之比，称为位移动力系数。
简谐荷载作用下，与之间关系曲线分析。
1、无阻尼条件
（1） 0 时， 5.0
1, ymax ( t ) yst。
4.0
（2）0 1 0 时，
随着增加增大，
3.0
0
FP ( t ) FP sint。 y( t ) yst sint。
（3）当ξ=1时的阻尼称为临界阻尼；相应的值称为
临界阻尼系数，用cr 表示，则
cr 2mk 2m ，
k 2mk 2m cr
阻尼比即为阻尼系数与临界阻尼系数 cr 之比。
§14-4 单自由度结构在简谐荷载作用下的强迫振动
当干扰力 F(t) 直接作用在质点上，质点的受力将如图14-10所示，
且 y( t )与FP ( t ) 同步。
2.0
（3） 1 时， 1.0
, ymax ( t ) , 共振。
（4）1 时，
1.0 2 2.0
3.0
随着增加减小，且 y( t )与 FP ( t ) 反向。
（5）时， 0, 在静平衡位置附近作微小
振动。
y0
cos 't
y0
ky0
'
sin
't
y bekt sin( 't ')
其中
b
y02
(ห้องสมุดไป่ตู้
y0
ky0
'
)2
tan ' ' y0
/ 为有阻尼自振频率。
y0 ky0
令 k ，称为阻尼比。
' 2 k2 1 ( k )2 1 2
通常当ξ<0.1时，则 ' 和的差别很小。

第2章单自由度系统的自由振动

25第2章单自由度系统的自由振动2.1 无阻尼系统的自由振动设有质量为m 的物块(可视为质点)挂在弹簧的下端，弹簧的自然长度为l 0,弹簧刚度为k ，如不计弹簧的质量，这就构成典型的单自由度系统，称之为弹簧质量系统如图2-1所示。

工程中许多振动问题都可简化成这种力学模型。

例如，梁上固定一台电动机，当电机沿铅直方向振动时，梁和电机组成一个振动系统，如不计梁的质量，则它在该系统中的作用相当于一根无重弹簧，而电机可视为集中质量。

于是这个系统可简化成如图2-1所示的弹簧质量系统。

2.1.1自由振动方程以图2-1所示的弹簧质量系统为研究对象。

取物块的静平衡位置为坐标原点O ，x 轴顺弹簧变形方向铅直向下为正。

当物块在静平衡位置时，由平衡条件∑F x = 0，得到st δk mg = （A ）st δ称为弹簧的静变形。

当物块偏离平衡位置为x 距离时，物块的运动微分方程为mxkx &&=− （2-1）将式（2-1）两边除以m ，并令mkp =n （2-2）则式（2-1）可写成02n =+x p x && （2-3）这就是弹簧质量系统置之只在线弹性力－kx 的作用下所具有的振动微分方程，称之为无阻尼自由振动的微分方程，是二阶常系数线性齐次方程。

由微分方程理论可知，式（2-3）的通解为t p C t p C x n 2n 1sin cos +=其中C 1和C 2为积分常数，由物块运动的起始条件确定。

设0=t 时，x x xx ==00，&&。

可解得 C x 10= n02p xC &=t p p xt p x x n n0n 0sin cos &+= （2-4）式（2-4）亦可写成下述形式)sin(n α+=t p A x （2-5）26 其中⎪⎪⎩⎪⎪⎨⎧=+=)arctan()(00n 2n020x x p p x x A &&α （2-6）式（2-4）、（2-5）是物块振动方程的两种形式，称为无阻尼自由振动，简称自由振动。

02第二讲：运动方程的建立

2015/10/8
第二讲：运动方程的建立
一、基本动力体系一、基本动力体系
两个典型的单自由度体系
第二讲：运动方程的建立
二、建立运动微分方程常用方法
1. 牛顿（牛顿（Newton Newton））第二定律
F ma
物理元件：质量集中质量m 集中质量m 阻尼器阻尼系数阻尼系数c c 弹簧弹簧刚度弹簧刚度k k
t1
2 1
t2
单质点系的受力图
cu ku p(t ) mu
T —— 体系的动能； V —— 体系的位能，包括应变能及任何保守力的势能； Pncj—— ——与与uj相应的非保守力（包括阻尼力及任意外荷载相应的非保守力（包括阻尼力及任意外荷载）。）。
用Hamilton 原理推导原理推导Lagrange Lagrange 方程
1 1 2 V ku 2 W p(t )u f D u T mu 2 2
T ( s, t ) W ( s , t ) V ( s, t )dt 0
t1
t2
u cu u kuu p (t )u dt 0 mu t u cu u kuu p (t )u dt 0 t mu
u t2 mu udt mu udt mu
t1 t1
第二讲：运动方程的建立
单质点体系的受力分析
F p(t ) f D f s
ma f D f s p (t )
au
f D cu
(a) 单层框架结构
两个力学模型完全等效因为两个体系的运动方程相同单自由度系统虽然简单，但是包含了单自由度系统虽然简单，但是包含了结构动力学的全部思想和方法。多自由度系统还可通过振型迭加法转多自由度系统还可通过振型迭加法转化为单自由度系统，因此学习它非常重要。

单自由度体系结构的地震反应(2)

g
• 动力系数(放大倍数）
＝ Sa
xg max
7
建筑结构抗震单自由度体系的地震反应
二、地震影响系数
• 地震系数 k＝ xg max
g
反应地面运动强烈程度。一般，地震烈度愈大，地面运动加速度愈大，地震系数也愈大，因而，地震系数与地震烈度之间有一定的对应关系。
地震烈度与地震系数的关系
地震烈度
6
7
2 1+0.05 0.08+1.6
20
建筑结构抗震单自由度体系的地震反应六、《抗震规范》设计反应谱
2. 地震影响系数曲线的确定 1)选用国内、外近300条地震纪录，按场地类别归类，统计拟合出标准地震影响系数曲线。
2)谱曲线的峰值 max ：取决于设防烈度
表5-5 水平地震影响系数最大值αmax
对应关系，这样给定任一地面运动，即可做出一条a-T 曲线称作加速度反应谱曲线。
13
建筑结构抗震单自由度体系的地震反应四、地震反应谱
反应谱曲线的特点 1）多峰值；2)阻尼影响大；3)随周期变化规律显著
El Centro波加速度反应谱
El Centro波速度反应谱
14
建筑结构抗震单自由度体系的地震反应五、设计地震反应谱
地震系数k 0.05
0.1
表3-3
8
9
0.2
0.4
8
建筑结构抗震单自由度体系的地震反应二、地震影响系数
• 动力系数(放大倍数）＝ Sa xg max
反应单质点体系最大绝对加速度与地面运动最大加速度的比值，表示由于动力效应，质点的最大绝对加速度比地面运动最大加速度放大了多少倍.
9
建筑结构抗震单自由度体系的地震反应三、水平地震作用的计算

《振动力学》2单自由度系统自由振动

单位：弧度/秒（rad/s）
则有： &x& + ω02 x = 0
通解： x(t) = c1 cos(ω0t) + c2 sin(ω0t) = Asin(ω0t + ϕ)
c1, c2：任意常数，由初始条件决定
振幅： A = c12 + c22
初相位： ϕ = tg −1 c1
c2
4
单自由度系统自由振动
解法2：
平衡位置2
动能 T = 1 Iθ&2 = 1 ml2θ&2
最大位移位置，系统动能为零，势能达到最大
ω0 = k / m
T +V = const
Tmax = Vmax
Tmax = 0
Vmax
=
1 2
kxm2 ax
m
k
最大位移位置
0
xmax
静平衡位置
x
x&max = ω0 xmax
x 是广义的对于转动： θ&max = ω0θmax
x(t) = Asin(ω0t + ϕ) 30
无阻尼的质量弹簧系统受到初始扰动后，其自由振动是以 ω0 为频率的简谐振动，并且永无休止。
x
T = 2π / ω 0
初始条件的说明：
初始条件是外界能量输入的一 x0
A
种方式，有初始位移即输入了弹性势能，有初始速度即输入了动能。
ϕ0
ω0
t
9
单自由度系统自由振动
零初始条件下的自由振动：
x(t)
=
x0
&x& + ω02 x = 0
ω0 =
k m

3—2 单自由度体系的弹性地震反应分析

fr = −kx(t)
(3-3)
式中 k——弹性直杆的刚度，即质点产生单位水平位移时， ——弹性直杆的刚度即质点产生单位水平位移时，弹性直杆的刚度，在质点上所需施加的水平力，在质点上所需施加的水平力，负号表示恢复力的方向总是和质点位移方向相反。和质点位移方向相反。
阻尼力是使结构体系振动逐渐衰减的力阻尼力是使结构体系振动逐渐衰减的力，反映了造是使结构体系振动逐渐衰减的力，成系统能量耗散的诸因素( 如材料内摩擦、成系统能量耗散的诸因素 ( 如材料内摩擦、构件连接处的摩擦、空气阻尼等) 的作用。接处的摩擦、空气阻尼等 ) 的作用。通常采用便于计算的粘滞阻尼理论，计算的粘滞阻尼理论，即假定阻尼力的大小与质点的相对速度成正比，的相对速度成正比，而力的方向与相对速度的方向相反，相反，即 fc = −cx(t) ɺ (3-2)
2
x ɺɺ(t) + 2ζωx(t) +ω x(t) = 0 ɺ
(3—10) 10)
上式为有阻尼单自由度体系自由振动的运动方程，上式为有阻尼单自由度体系自由振动的运动方程，方程等号右边荷载项为零，程等号右边荷载项为零，表示体系在振动过程中无外部干扰作用，部干扰作用，振动是由初始位移或初始速度或两者共同影响而引起的。同影响而引起的。
fI = −m[ɺɺg (t) + ɺɺ(t)] x x
式中负号表示惯性力的方向与绝对加速度的方向相反。式中负号表示惯性力的方向与绝对加速度的方向相反。
弹性恢复力是使质点从振动位置恢复到平衡位置的一种力，它是由质点支承杆弹性变形引起的，一种力，它是由质点支承杆弹性变形引起的，其大正比，小与质点的相对位移成 x(t) 正比，即

单自由度振动系统的运动方程及其解析解

单自由度振动系统的运动方程及其解析解单自由度振动系统是指只有一个自由度的振动系统，其运动方程可以用一个二阶常微分方程表示。

在这篇文章中，我们将讨论单自由度振动系统的运动方程及其解析解。

1. 引言振动是自然界中一种常见的现象，也是物体在受到扰动后产生的周期性运动。

单自由度振动系统是研究振动现象的基本模型，它可以用来描述弹簧振子、摆锤等物理系统的振动。

2. 运动方程的建立对于单自由度振动系统，其运动方程可以通过牛顿第二定律推导而来。

假设系统的质量为m，位移为x，系统受到的外力为F，弹性系数为k，则可以得到如下的运动方程：m*x'' + k*x = F3. 简谐振动的解析解当外力为零时，即F=0，单自由度振动系统的运动方程简化为：m*x'' + k*x = 0这是一个常系数线性齐次二阶常微分方程，可以通过特征方程的方法求解。

假设解为x(t) = A*cos(ωt + φ)，代入方程中可以得到：-m*ω^2*A*cos(ωt + φ) + k*A*cos(ωt + φ) = 0整理得到：(ω^2*m - k)*A*cos(ωt + φ) = 0由于A*cos(ωt + φ)不为零，所以可以得到特征方程：ω^2*m - k = 0解特征方程可以得到系统的固有频率：ω = sqrt(k/m)因此，单自由度振动系统的解析解为：x(t) = A*cos(ωt + φ)其中A和φ为待定常数，分别表示振幅和相位。

4. 非简谐振动的解析解当外力不为零时，即F≠0，单自由度振动系统的运动方程为：m*x'' + k*x = F这是一个非齐次线性二阶常微分方程，可以通过特解和通解的方法求解。

首先求解齐次方程，得到通解：x_h(t) = A*cos(ωt + φ)然后求解非齐次方程的特解，可以通过待定系数法或者复数法得到特解。

最后将通解和特解相加，得到系统的解析解：x(t) = x_h(t) + x_p(t)其中x_h(t)为齐次方程的通解，x_p(t)为非齐次方程的特解。

单自由度振动系统的运动方程解析解的振动幅度研究

单自由度振动系统的运动方程解析解的振动幅度研究单自由度振动系统是一种物理系统，其运动方程可以通过解析方法得到振动幅度的研究。

在这篇文章中，我们将探讨单自由度振动系统的运动方程解析解，并研究振动幅度的表达式。

1. 引言单自由度振动系统是指只有一个自由度的振动系统，例如简谐振动器。

在工程和物理学中，单自由度振动系统的研究非常重要，因为它可以帮助我们理解更为复杂的振动系统。

2. 单自由度振动系统的运动方程单自由度振动系统的运动方程可以通过牛顿第二定律得到。

假设系统质量为m，弹性系数为k，阻尼系数为c，则其运动方程可以写为：m * x''(t) + c * x'(t) + k * x(t) = F(t)其中，x(t)是系统在时间t的位移，x'(t)和x''(t)分别是x(t)的一阶和二阶导数，F(t)是外力。

3. 没有外力的情况在没有外力作用下的情况下（F(t) = 0），上述运动方程可以简化为：m * x''(t) + c * x'(t) + k * x(t) = 04. 弹簧阻尼器情况考虑到弹簧阻尼器的情况，即运动方程中包含了阻尼系数c。

当没有外力作用下的情况下，上述运动方程可以写为：m * x''(t) + c * x'(t) + k * x(t) = 0为了求解该线性齐次方程，可以猜测x(t)的解为e^(rt)，其中r是待定常数。

将猜测解带入方程，得到特征方程：m * r^2 + c * r + k = 0解特征方程，可以得到r的值。

根据r的值的不同情况，振动系统的运动可以分为三种情况：欠阻尼、过阻尼和临界阻尼。

5. 欠阻尼情况当特征方程的根为复数时，振动系统处于欠阻尼情况。

对于欠阻尼情况，振动系统的解可以写为：x(t) = e^(-ζωn*t) * [A * cos(ωd * t) + B * sin(ωd * t)]其中，ζ是阻尼比，ωn是系统的自然角频率，A和B是常数，ωd 是阻尼角频率。

单自由度体系强迫振动.ppt

1
2 2
yst
1
2 2
,
于是有:
C2 0
于是有:
y(t)
yst
1
1
2 2
(sint sin t)
10 12
yst (sint sin t)
强迫振动的过程可分为两个组成部分,第一部分按荷载频率作纯强迫振动,第二部分按自振频率作自由振动。振动开始时两种振动并存，称为“过渡阶段”或“瞬态”，由于实际振动中存在阻尼力，故经过一段时间后，将只剩下第一部分仍在振动，第二部分则“衰减”掉了，这一
§10-3 单自由度体系的强迫振动
强迫振动---动荷载引起的振动,又称受迫振动。
3.1 简谐荷载作用下的受迫振动(不计阻尼)
一.运动方程及其解
Fp(t) Fp sint
my(t) k11 y(t) Fp sint FP(t) m
y(t)
或
y(t)
2
y(t)
Fp
s in t 10
11
l
EI
m
3.1 简谐荷载作用下的受迫振动(不计阻尼)
=1
FP
运动方程
振幅
y(t) 12FP sint 11(my)
my(t) 1 y(t) 12 FP sin t
11
11
令
Fp
12 11
FP
A
Fp
m 2
Fp11
12 11
FP11
12FP
yst
my(t
稳态解
)
1
11
y (t )
y(t) Fp
Fp
m 2
sin t s in t
仍是位移动力系数是内力动力系数吗?

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

柔度法) 二、列位移方程(柔度法列位移方程柔度法对于不便于计算刚度系数的体系，对于不便于计算刚度系数的体系，也可改用结构的柔度系数来建立运动方程。这种方法以整个休系为研究对象，如图所示，立运动方程。这种方法以整个休系为研究对象，如图所示，在振动的任一时刻t，质点m上除作用有动力荷载上除作用有动力荷载P(t)外，还有惯性力动的任一时刻，质点上除作用有动力荷载外 I(t)、阻尼力R(t)，不考虑重力，又由于弹性恢复力是内力，故图、阻尼力，不考虑重力，又由于弹性恢复力是内力，中未标出。质点m的动位移看成是由于动力荷载、的动位移y(t)看成是由于动力荷载中未标出。质点的动位移看成是由于动力荷载、惯性力和阻尼力共同引起的，根据叠加原理，尼力共同引起的，根据叠加原理，可得
§11-2 单自由度体系的运动方程
• 动力计算的基本未知量是质点的位移，它是时间t的函数。为
了求出动力反应，应先列出求解质点位移的方程。描述体系振动时质点动位移的数学方程，称为体系的运动方程(或振动方程)。
•建立运动方程常用的方法是动静法。根据达朗贝尔原理，将惯
性力假想地作用在质点上，在振动的每一瞬时，惯性力与结构受到的动荷载、约束反力等在形式上组成一平衡力系(动平衡)，于是就可以利用静力学中的方法建立运动方程。
即
建立图示体系的运动方程。图中质点m 例11-1 建立图示体系的运动方程。图中质点 1=2m、m2=m，弹、，性支座B的刚度系数为忽略阻尼影响和刚性杆的分布质量的刚度系数为k 忽略阻尼影响和刚性杆的分布质量。性支座的刚度系数为 1,忽略阻尼影响和刚性杆的分布质量。
解：这是两个质点的单自由度体系。设在振动的任一时刻t刚性这是两个质点的单自由度体系。设在振动的任一时刻刚性杆绕铰A的转角为顺时针为正，则质点m 杆绕铰的转角为α (t ) ，顺时针为正，则质点 1、m2的惯性力分别为 3 3 l && && I 2 (t ) = − m2 ⋅ lα (t ) = − mlα (t ) &&(t ) = − ml α&(t ) & I1 (t ) = − m1 ⋅ α 2 2 2
刚度法) 一、列动力平衡方程(刚度法列动力平衡方程刚度法利用平衡条件建立运动方程
图11-10
在振动的任一时刻t取质点为隔离体作用在质点上的力有各力以指向y(t)的正在振动的任一时刻取质点m为隔离体作用在质点上的力有各力以指向的正取质点为隔离体作用在质点上的力有(各力以指向方向为正)：方向为正： (1)重力。重力W。重力 (2)动力荷载动力荷载P(t)。动力荷载。
图示体系，各杆EI=常数，忽略杆件的分布质量和阻常数，例11-2 图示体系，各杆常数尼影响，建立其运动方程。尼影响，建立其运动方程。
图11-13
解：图示体系为静定结构，求柔度系数比较方便，宜列位移图示体系为静定结构，求柔度系数比较方便，方程。方程。
y (t ) = δ11[− m&&(t )] + δ1P ⋅ P(t ) y
1 1 2 2 1 2 l3 δ11 = ( ×l × l + ×l ×2l × ×l) = EI 2 3 2 3 EI 1 1 l l l3 δ1P = ( × 2l × × ) = EI 2 2 2 4EI
运动方程为
&&( t ) + y
EI 1 y (t ) = P (t ) 3 ml 4m
y 沿动位移沿动位移y(t)的正向作用。的正向作用。惯性力 −m&&(t ) 的正向作用
(5)阻尼力阻尼力R(t)。关于阻尼力的理论有多种，这里采用计算较简单阻尼力。关于阻尼力的理论有多种，的粘滞阻尼理论。它假定阻尼力R(t)与质点速度成正比，方向与速与质点速度成正比，的粘滞阻尼理论。它假定阻尼力与质点速度成正比度的方向相反，度的方向相反，即
图11-11
y (t ) = δ11[I (t ) + R(t ) + P(t )]
即
& m&&(t ) + cy (t ) + y 1
δ11
y (t ) = P (t )
为柔度系数，式中 δ11为柔度系数，它表示在质点上沿质点运动方向施加单位力引起质点沿运动方向的静位移。柔度系数与刚度系数k 互为倒数. 质点沿运动方向的静位移。柔度系数与刚度系数 11互为倒数.由于建立运动方程要用到体系的柔度系数，所以又称为柔度法。立运动方程要用到体系的柔度系数，所以又称为柔度法。
弹性支座B的反力弹性支座的反力为
RB = k1lα (t )
得由Leabharlann ΣM A = 0I1 (t ) ⋅
l 3 + I 2 (t ) ⋅ l − RB ⋅ l = 0 2 2
将I1(t)、I2(t)和RB的表达式代入上式并整理得运动方程、和
4k1 && α (t ) + α (t ) = 0 11m
因质点重力W与由其引起的静位移 ∆ st 的关系为 W = k11∆ st ，因质点重力与由其引起的静位移于是得出质点振动的运动微分方程为
& m&&(t ) + cy (t ) + k11 y (t ) = P(t ) y
式表明，式表明，若建立体系的运动方程时以静平衡位置作为计算位移的起点，则所得动位移的微分方程与重力无关。的起点，则所得动位移的微分方程与重力无关。以后在建立体系的运动方程时，将不标出重力W及其产生的静位移系的运动方程时，将不标出重力及其产生的静位移∆ st 。上述方法是直接利用达朗贝尔原理建立质点m在任一瞬时的动上述方法是直接利用达朗贝尔原理建立质点在任一瞬时的动力平衡方程，它要用到结构的刚度系数k 所以又称为刚度法。力平衡方程，它要用到结构的刚度系数 11，所以又称为刚度法。
图11-10
(3)弹性恢复力弹性恢复力S(t)。它是由于杆件的弹性变形而施加于质点的力，它的大弹性恢复力。它是由于杆件的弹性变形而施加于质点的力，小与质点的位移成正比，但方向相反，小与质点的位移成正比，但方向相反，即
S (t ) = −k11 [∆ st + y (t )]
为刚度系数，式中 k11 为刚度系数，其意义是使质点沿运动方向产生单位静位移而需在质点上沿运动方向施加的力。点上沿运动方向施加的力。 (4)惯性力。其大小为质点质量与质点加速度的乘积，方向与加速度的惯性力I(t)。其大小为质点质量m与质点加速度的乘积与质点加速度的乘积，惯性力方向相反，方向相反，即 I (t ) = − m&&(t ) y
& R (t ) = −cy (t )
式中c称为粘滞阻尼系数。式中称为粘滞阻尼系数。称为粘滞阻尼系数考虑质点m的动力平衡考虑质点的动力平衡ΣY=0，应有的动力平衡，
I (t ) + R (t ) + S (t ) + P (t ) + W = 0
即
& m&&(t ) + cy (t ) + k11[∆ st + y (t )] = P (t ) + W y

第二节单自由度体系的运动方程

合集下载