04.20 初三下 一模基础拓展题复习

初三下学期第一次模拟考试语文试卷（带解析） 考试时间：120分钟 考试总分：100分第1题：下列各组句子中，加点词语的字形和加点字的读音__都正确__的一项是（ ）（2分） A ．干__涸__(hé)__汲__取(xí)__恪__守(kè)消声__匿__迹(nì) B ．__蓦__然(mò)__拮__据(jié)__亘__古(ɡèn)__锲__而不舍(qiè) C ．__凛__冽(lǐn)__氛__围(fēn)__赢__弱(léi)惟妙惟__肖__(xiāo) D ．__侧__隐(cè)匀__称__(chènɡ) 旁__鹜__(wù)__冥__思遐想(mínɡ) 【答案】：B 【解析】： 试题分析：此类型的题目考查学生对字词的理解识记能力，考查等级为A 。

需要学生在平时多读课文，养成熟练地语感，注意读准拼音，多读课下注释，多查字典等工具书。

A ．__汲__取(jí)C．惟妙惟__肖__(xiào )D．匀__称__(chèn) 考点：识记并正确书写现代汉语普通话常用字的字音。

能力层级为识记A 。

第2题：下列加点词语运用__不正确__的一项是（ ）（2分） A ．在今年结束的澳大利亚网球公开赛中，中国金花李娜的表现相当给力，以二比零直落两盘，击败齐布尔科娃获得冠军，其精湛的球技令人__叹为观止__。

B ．城市建设不是面子工程，不应__作秀__，而应当将改善人民群众的生活条件，提高广大市民的综合素质作为中心工作来抓。

C ．升学不要太钻牛角尖，所谓“__条条大路通罗马__”，只要认真努力，每一条道路都一定可以走向成功。

D ．“我读经典”系列读书活动深受我市青少年欢迎，同学们__趋之若鹜__，从中吸取文化精髓。

【答案】：D姓名：________________ 班级：________________ 学号：________________--------------------密----------------------------------封 ----------------------------------------------线----------------------【解析】：试题分析：趋之若鹜,比喻像鸭子一样去追赶,是贬义词．考点：正确使用词语（包括熟语）。

初三一模数 学1.在疫情防控的特殊时期，为了满足初三高三学生的复习备考需求，北京市教委联合北京卫视共同推出电视课堂节目《老师请回答特别节目“空中课堂”》，在节目播出期间。

全市约有200 000名师生收看了节目.将200 000用科学记数法表示应为 A.0.2×105B.0.2×106C.2×105D.2×1062.下列图形中，是轴对称图形的是3.在数轴上，表示实数a 的点如图所示，则2−a 的值可以为A.−5.4B.−1.4C.0D.1.44.以AB =2cm,BC =3cm,CD =2cm,DA =4cm 为边画出四边形ABCD，可以画出的四边形个数为A. 0B. 1C. 2D.无限多5.在一个长2分米、宽1分米、高8分米的长方体容器中，水面高5分米,把一个实心铁块缓慢浸入这个容器的水中，能够表示铁块浸入水中的体积y (单位:分米3)与水面上升高度x (单位:分米)之间关系的图象的是6. 如果a 2+a −1=0,那么代数式(1−a−1a 2+2a+1)÷aa+1的值是A. 3B. 1C. −1D. −37.在平面直角坐标系xOy 中，点A(−1,2),B(2,3),y =ax 2的图象如图所示，则a 的值可以为 A. 0.7 B. 0.9 C. 2 D. 2.18.改革开放以来，人们的支付方式发生了巨大转变，近年来，移动支付已成为主要的支付方式之一，为了解某校学生上个月A,B 两种移动支付方式的使用情况，从全校1000名学生中随机抽取了100人，发现样本中A,B 两种支付方式都不使用的有5人，样本中仅使用A 种支付方式和仅使用B 种支付方式的学生的支付金额a (元)的分布情况如下:支付金额a （元）支付方式0<a ≤1000 1000<a ≤2000 a >2000仅使用A 18人 9人 3人 仅使用B10人14人1人①从样本中使用移动支付的学生中随机抽取一名学生，该生使用A 支付方式的概率大于他使用B 支付方式的概率;②根据样本数据估计，全校1000名学生中。

物理参考答案一、选择题（每小题只有一个选项正确，共24分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案BACDDBCBBCCD二、填空题（24分，每空1分）13．运动 弹性势 人耳14．水平 52 2.6×10315．电磁波 变化 电能 16．费力 10 不变17．导体 热 电流相同，中间窄电阻大，产生的热量多18．400竖直（垂直） 紧贴纸板 19．0.1 120 90 20．小 大于 sGρ2三、解答题 21．（6分）22．本题共6分 解：（1）tsv =1分 s m 5s602m600=⨯=v 1分 （2）G =mg =（60kg+15kg ）×10N/kg=750NF =G =750N 1分Pa 102.5m103N 750523⨯=⨯==-S F p 1分 （3）∵匀速∴F =f =20N 1分w 100s602m 600N 20=⨯⨯=⨯==t s F t w p 1分 说明：本题其它解法合理，同样给分23．本题共9分。

（1） A 0.8Ω10V8111===R U I 1分 ∵串联 1分∴I 2=I 1=0.8A 1分甲A O 空气水 电源乙-丙（2）UIt W = 1分J 120s 10A 0.8V 15=⨯⨯=W 2分 （3）由题意分析知，电路中允许通过的最大电流为1A 1分R 1两端的最大电压为V 10Ω10A 1111=⨯=⨯=R I U 1分 R 2两端的最小电压V 5V 10V 1512=-=-=U U U 1分 说明：本题其它解法合理，同样给分24．（6分，最后一空2分，答对一点给1分，其余每空1分） （1）水升高的温度（2）燃料燃尽后的水温t （写加热后的水温不得分） cm 2(t -t 0)（3）不能 花生米和酒精完全燃烧放出的热量没有全部被水吸收，有热损失；不能确定酒精燃烧放出的热量 25．（7分，每空1分，作图2分） （1）1.0N（2）见右乙图（没有延长过原点得1分） （3）能 由表中数据分析知物体浸没时随着深度的增加，浮力大小不变（4）液体密度（写密度不给分），1.1×10326．（8分，每空1分，作图2分） （1）见右甲图（2）灯泡与灯座接触不良 （写灯泡断路不给分） （3）移动滑片，使电压表示数等于2.5V（只写移动滑片不给分） （4）0.3 0.75 （5）2四组数据中，第2组数据偏离灯丝电阻随温度的升高而增大的事实27．（10分，每小题2分） （1）磁 （2）改变 （3）B （4）1101 （5）A乙2 4 6 8 10 12 14F 1/Nh /cm甲SVABA×。

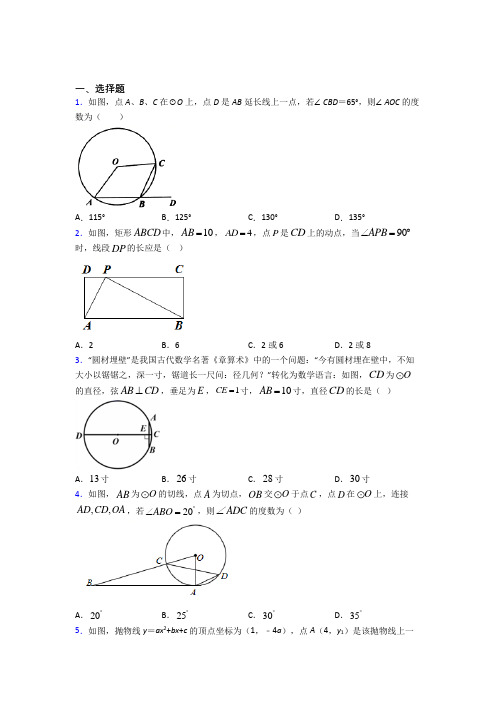
一、选择题1．如图，点A 、B 、C 在⊙O 上，点D 是AB 延长线上一点，若∠CBD ＝65°，则∠AOC 的度数为（ ）A ．115°B ．125°C ．130°D ．135°2．如图，矩形ABCD 中，10AB =，4=AD ，点P 是CD 上的动点，当90APB ∠=︒时，线段DP 的长应是（ ）A ．2B ．6C ．2或6D ．2或83．“圆材埋壁”是我国古代数学名著《章算术》中的一个问题：“今有圆材埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺问：径几何？”转化为数学语言：如图，CD 为O的直径，弦AB CD ⊥，垂足为E ，1CE =寸，10AB =寸，直径CD 的长是（ ）A ．13寸B ．26寸C ．28寸D ．30寸4．如图，AB 为O 的切线，点A 为切点，OB 交O 于点C ，点D 在O 上，连接,,AD CD OA ，若20ABO ︒∠=，则ADC ∠的度数为（ ）A ．20︒B ．25︒C ．30︒D ．35︒5．如图，抛物线y ＝ax 2+bx +c 的顶点坐标为（1，﹣4a ），点A （4，y 1）是该抛物线上一点，若点B （x 2，y 2）是该抛物线上任意一点，有下列结论：①4a ﹣2b +c ＞0；②抛物线y ＝ax 2+bx +c 与x 轴交于点（﹣1，0），（3，0）；③若y 2＞y 1，则x 2＞4；④若0≤x 2≤4，则﹣3a ≤y 2≤5a ．其中，正确结论的个数是（ ）A ．0B ．1C ．2D ．36．二次函数y ＝ax 2+bx +c （a ，b ，c 为常数，且a ≠0）中的x 与y 的部分对应值如表： x ﹣1 0 1 3 y ﹣1353则代数式﹣2a（4a +2b +c ）的值为（ ） A ．92 B ．152C ．9D ．157．如图，已知二次函数()20y ax bx c a =++≠的图象与x 轴交于点()1,0A -，对称轴为直线1x =，下列结论：①0abc <；②930a b c ++=；③20a b +=；④2am bm a b +<+（m 是任意实数），其中正确的是（ ）A ．①②B ．②③C ．①②③D ．②③④8．如图，抛物线2y ax bx c =++的顶点位于第二象限，对称轴是直线1x =-，且抛物线经过点(1,0)．下面给出了五个结论：①0abc >；②240a b c -+>；③40a c +<；④13a b c -=；⑤326320a b c --<．其中结论正确的有（ ）A ．5个B ．4个C ．3个D ．2个9．下表是小亮填写的实践活动报告的部分内容： 题目测量树顶到地面的距离测量目标示意图相关数据30AB =米，28α∠=︒，45β∠=︒A ．()30tan 28x x =-︒B ．()30tan 28x x =+︒C ．30tan 28x x +=︒D ．30tan 28x x -=︒10．在Rt ABC △中，90C ∠=︒，1cos 3B =，则tan A 的值为（ ） A ．3 B ．3 C ．24D ．1010311．如图，△ABC 中，AB =AC =5，BC =8，则sin B 的值为（ ）A ．58B ．45C ．35D ．1212．在ABC 中，AB 122=，AC 13=，2cos B 2∠=，则BC 边长为（ ） A ．7B ．8C ．8或17D ．7或17二、填空题13．如图，在平面直角坐标系中，过点()11,0A 作x 轴的垂线交直线y x =于点B ，以О为圆心，1OB 为半径作弧，交x 轴于点2A ；过点2A 作x 轴的垂线交直线y x =于点2B ，以O 为圆心，2OB 为半径作弧，交x 轴于点3A ；过点3A 作x 轴的垂线交直线y x =于点3B ，以О为圆心，3OB 为半径作弧，交x 轴于点4A ，……，按此做法进行下去，设由11A B ，12A A ，弧21A B 围成的图形面积记为1S ，由22A B ，23A A ，弧32A B 围成的图形面积记为2S ，由33A B ，34A A ，弧43A B 围成的图形面积记为3S ，……，那么2020S 为_______：14．如图，AB 是O 的直径，弦CD AB ⊥，垂足为点M ．连接,OC DB ，如果//,23OC DB OC =，那么图中阴影部分的面积是______15．将二次函数()2y a x m k =++（0a ≠）的图象先向右平移3个单位长度，再向下平移2个单位长度，所得图象的表达式是()214y x =-+，则原函数的表达式是________． 16．二次函数2y ax bx c =++的图象如图所示，有如下结论：①0abc >；②20a b -=；③320b c +>；④2(am bm a b m +≤-为实数)．其中正确结论是_____________（只填序号)．17．将二次函数245y x x =-+化为()2y x h k =-+的形式，则y =________________．18．如图，矩形ABCD 中，AE ＝13AD ，将△ABE 沿BE 折叠后得到△GBE ，延长BG 交CD 于F 点，若CF ＝FD ＝3，则BC 的长为_____．19．在ABC 中，90C ∠=︒，若5sin 13B =，则cos A =________． 20．如图，在△ABC 中，∠A ＝30°，∠B ＝45°，BC ＝6cm ，则AB 的长为_____．21．如图，一艘轮船在小岛A 的北偏东60°方向且距小岛80海里的B 处，沿正西方向航行一定时间后到达小岛的北偏西45°的C 处，则该船航行的路程为_____海里．22．直角三角形ABC 中，∠B ＝90°，若cosA ＝35，AB ＝12，则直角边BC 长为___． 三、解答题23．一块含有30角的三角板ABC 如图所示，其中90C ∠=︒，30A ∠=︒，3BC cm =．将此三角板在平面内绕顶点A 旋转一周．（1）画出边BC 旋转一周所形成的图形； （2）求出该图形的面积． 24．（概念认识）定义：对角线互相垂直且相等的四边形叫做垂等四边形．（1）如图1，已知在垂等四边形ABCD 中，对角线AC 与BD 交于点E ，若AB AD ⊥，4AB =cm ，4cos 5ABD ∠=，求AC 的长度，（数学理解）（2）在探究如何画“圆内接垂等四边形”的活动中，小李与同学讨论出了如下方法：如图2，在O 中，已知AB 是O 的弦，只需作OD OA ⊥，OC OB ，分别交O 于点D和点C ，即可得到垂等四边形ABCD ，请你写出证明过程． （问题解决） （3）如图3，已知A 是O 上一定点，B 为O 上一动点，以AB 为一边作出O 的内接垂等四边形（A 、B 不重合且A 、B 、O 三点不共线），对角线AC 与BD 交于点E ，O 的半径为22，当点E 到AD 的距离为3时，求弦AB 的长度．25．已知二次函数y ＝ax 2+bx ﹣2（a ≠0）的图像与x 轴交于点A 、B ，与y 轴交于点C ． （1）若点A 的坐标为（4，0）、点B 的坐标为（﹣1，0），求a +b 的值；（2）若图像经过P （1，y 1），Q （m ，n ），M （3，y 2），N （3﹣m ，n ），试比较y 1、y 2的大小关系；（3）若y ＝ax 2+bx ﹣2的图像的顶点在第四象限，且点B 的坐标为（﹣1，0），当a +b 为整数时，求a 的值．26．如图，在平面直角坐标系中，已知AOB ，90AOB ∠=︒，AO BO =，点A 的坐标为()3,1-．（1）求点B的坐标．（2）求过点A，O，B的二次函数的表达式．AB B的面积．（3）设点B关于二次函数的对称轴l的对称点为1B，求1【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】求出∠ABC，再求出它所对的弧对的圆心角，即可求∠AOC．【详解】解：∵∠CBD＝65°，∴∠ABC=180°-65°=115°，优弧AC所对的圆心角的度数为：115°×2=230°，∠AOC=360°-230°=130°，故选：C．【点睛】本题考查了圆周角的性质，解题关键是求出圆周角，根据同弧所对的圆周角和圆心角的关系求角．2．D解析：D【分析】以AB的中点O为圆心，AB的一半5为半径作圆，交CD于点P，点P即为所求；设PC=x，则PD=10-x，证△ADP∽△PCB，对应边成比例列方程，解之可得答案．【详解】如图，以AB的中点O为圆心，AB的一半5为半径作圆，交CD于点P，点P即为所求；设PC= x，则PD= 10- x，∵四边形A BCD 是矩形， ∴∠D=∠C= 90° ∴∠DAP+∠APD= 90° ∵∠APB= 90°， ∴∠APD +∠BPC= 90° ∴∠DAP=∠CPB ， ∴△ADP ∽△PCB ，∴AD DPPC CB = 即4104x x -=， 解得: x = 2或8， PD= 10-x= 2或8， 即PD = 2或8. 故选: D. 【点睛】本题主要考查圆周角定理和相似三角形的判定与性质及矩形的性质，熟练掌握圆周角定理和相似三角形的判定与性质是解题的关键.3．B解析：B 【分析】连接OA ．设圆的半径是x 寸，在直角△OAE 中，OA ＝x 寸，OE ＝x−1，在直角△OAE 中利用勾股定理即可列方程求得半径，进而求得直径CD 的长． 【详解】解：如图，连接OA ．设圆的半径是x 寸，在直角△OAE 中，OA ＝x 寸，OE ＝（x−1）寸， ∵222OA OE AE =+， ∵AB=10，且AB CD ⊥ ∴AE=12AB=5 则()22125x x =-+， 解得：x ＝13．则CD ＝2×13＝26（寸）．故选：B ． 【点睛】本题考查了垂径定理和勾股定理，正确作出辅助线是关键．4．D解析：D 【分析】根据切线的性质得∠OAB=90°，利用互余计算出∠AOB 的度数，然后根据圆周角定理得到∠ACD=35°，． 【详解】解：∵AB 为⊙O 的切线，点A 为切点， ∴OA ⊥AB ， ∴∠OAB=90°， ∴∠AOB=90°-20°=70°， ∵∠AOB=2∠ADC=70°， ∴∠ADC=12×70°=35°． 故选：D ． 【点睛】本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆周角定理．5．C解析：C 【分析】利用对称轴公式和顶点坐标得出﹣4a ＝a +b +c ，b ＝﹣2a ，c ＝﹣3a ，则可对①进行判断；抛物线解析式为y ＝ax 2﹣2ax ﹣3a ，配成交点式得y ＝a （x ﹣3）（x +1），可对②进行判断；根据二次函数对称性和二次函数的性质可对③进行判断；计算x ＝4时，y ＝5a ，则根据二次函数的性质可对④进行判断． 【详解】解：①∵二次函数y ＝ax 2+bx +c （a ≠0）的顶点坐标为（1，﹣4a ），∴x ＝﹣2ba＝1，且﹣4a ＝a +b +c ， ∴b ＝﹣2a ，c ＝﹣3a ，∵抛物线开口向上，则a ＞0，∴4a ﹣2b +c ＝4a +4a ﹣3a ＝5a ＞0，故结论①正确； ②∵b ＝﹣2a ，c ＝﹣3a ，∴y ＝ax 2﹣2ax ﹣3a ＝a （x ﹣3）（x +1），∴抛物线y ＝ax 2+bx +c 与x 轴交于点（﹣1，0），（3，0），故结论②正确； ③∵点A （4，y 1）关于直线x ＝1的对称点为（﹣2，y 1）， ∴当y 2＞y 1，则x 2＞4或x 2＜﹣2，故结论③错误； ④当x ＝4时，y 1＝16a +4b +c ＝16a ﹣8a ﹣3c ＝5a ，∴当0≤x 2≤4，则﹣4a ≤y 2≤5a ，故结论④错误． 故选：C ． 【点睛】本题考查了二次函数的图象与性质，掌握二次函数图象与性质的相关知识并能灵活运用所学知识求解是解题的关键．6．B解析：B 【分析】由当x=0和x=3时y 值相等，可得出二次函数图象的对称轴为直线x=32，进而可得出2b a -的值，由x=1时y=5，可得出当x=2时y=5，即4a+2b+c=5，再将2b a -=32及4a+2b+c=5代入2ba-（4a+2b+c ）中即可求出结论． 【详解】解：∵当x ＝0和x ＝3时，y 值相等， ∴二次函数图象的对称轴为直线x ＝32， ∴3=22b a -． ∵当x ＝1时，y ＝5，∴当x ＝2×32﹣1＝2时，y ＝5， ∴4a +2b +c ＝5．∴2b a -（4a +2b +c ）＝32×5＝152． 故选：B ． 【点睛】本题考查了二次函数图象上点的坐标特征以及二次函数的性质，利用二次函数的性质及二次函数图象上点的坐标特征，找出2ba-和（4a+2b+c ）的值是解题的关键． 7．B解析：B 【分析】①抛物线开口向上，对称轴为直线x ＝1，即可得出a ＞0、b ＜0、c ＜0，进而可得出abc ＞0，结论①错误；②由抛物线的对称轴以及与x 轴的一个交点坐标，可得出另一交点坐标为（3，0），进而可得出9a ＋3b ＋c ＝0，结论②正确；③由对称轴直线x=1，可得结论③正确；④2()()0am bm a b +-+≥，可得结论④错误．综上即可得出结论． 【详解】解：①∵抛物线开口向上，对称轴为直线x ＝1，∴a ＞0，12b a-=，c ＜0， ∴b ＝−2a ＜0，∴abc ＞0，结论①错误； ②∵二次函数y ＝ax 2＋bx ＋c （a≠0）的图象与x 轴交于点A （−1，0），对称轴为直线x ＝1，∴二次函数y ＝ax 2＋bx ＋c （a≠0）的图象与x 轴的另一个交点为（3，0），∴9a ＋3b ＋c ＝0，结论②正确；③∵对称轴为直线x ＝1， ∴12b a-=，即：b ＝−2a ， ∴20a b +=，结论③正确；④∵222()()(2)(2)2am bm a b am am a a am am a +-+=---=-+22(21)(1)a m m a m =-+=-≥0，∴2am bm a b +≥+，结论④错误．综上所述，正确的结论有：②③．故选：B ．【点睛】本题考查了抛物线与x 轴的交点、二次函数图象与系数的关系、二次函数的性质以及二次函数图象上点的坐标特征，逐一分析四条结论的正误是解题的关键．8．A解析：A【分析】由二次函数的图象即可判断a 、b 、c 的符号，即可判断①；由对称轴和与x 轴交点坐标即可求出c=-3a 和b=2a ，即可判断②③④；把()()()2232332632632236126=61a b c a a a a a a a a --=-⨯-⨯-=-+-变形之后即可判断⑤；【详解】∵由图象可知开口向下，∴a ＜0，∵对称轴为x=-1，∴ b ＜0，抛物线与y 轴的交点在原点上方，∴ c ＞0，∴ abc ＞0，故①正确；∵ 抛物线经过点(1，0)，对称轴为x=-1，∴ 抛物线与x 轴的另一交点时是(-3，0)，∴ a+b+c=0，∵对称轴为x=-1，∴ b=2a ，∴ a+2a+c=0，即c=-3a ，()24443150a b c a a a a -+=-+⨯-=-＞ ，故②正确；4430a c a a a +=-=＜ ，故③正确；123a b a a a c -=-=-= ，故④正确； ()()()2232332632632236126=61a b c a a a a a a a a --=-⨯-⨯-=-+- ，∵ ()21a -≥0，由图象得：1a ≠ ， ∴32632a b c --＜0，故⑤正确；故选：A ．【点睛】本题考查了二次函数图象的性质、对称轴以及函数值的求法，正确掌握二次函数的性质是解题的关键．9．B解析：B【分析】根据∠β=45°，得出BC ＝CD ＝x ，再根据28α∠=︒，用它的正切列方程即可．【详解】解：∵45β∠=︒，∴BC ＝CD ＝x ，∵AB ＝30，∴AC ＝x +30，∴tan28°＝30CD x AC x =+， ∴x ＝（x +30）tan28°，故选：B ．【点睛】 本题考查解直角三角形，解题的关键是熟练运用锐角三角函数的定义，本题属于基础题型．10．C解析：C【分析】 根据1cos 3B =，设AB=3x ，BC=x ，勾股定理求出AC ，根据三角函数的定义求tan A 即可． 【详解】解：在Rt ABC △中，90C ∠=︒，1cos 3B =， 设AB=3x ，BC=x ，2222(3)22AC AB BC x x x =-=-=， 2tan 422BC A AC x ===， 故选：C ．【点睛】本题考查了三角函数，解题关键是根据三角函数值确定直角三角形三边关系，再根据三角函数的意义计算． 11．C解析：C【分析】过A 点作AD BC ⊥交BC 于点D ，利用等腰三角形的三线合一求出BD ，利用勾股定理求出AD 即可解决问题．【详解】过A 点作AD BC ⊥交BC 于点D ，如图∵5AB AC ==，8BC =，∴4BD CD ==，∴2222543AD AB BD =--=， ∴3sin 5AD B AB ==． 故选：C ．【点睛】本题考查等腰三角形的性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．12．D解析：D【分析】首先根据特殊角的三角函数值求得B ∠的度数，然后分锐角三角形和钝角三角形分别求得BD 和CD 的长后即可求得线段BC 的长．【详解】解：∵2cos B 2∠=， ∴B 45∠=， 当ABC 为钝角三角形时，如图1，∵AB 122=，B 45∠=，∴AD BD 12==，∵AC 13=，∴由勾股定理得CD 5=，∴BC BD CD 1257=-=-=；当ABC 为锐角三角形时，如图2，BC BD CD 12517=+=+=，故选D ．【点睛】本题考查解直角三角形，解题的关键是明确余弦定理的内容、利用锐角三角函数解答．二、填空题13．【分析】根据点A 的取法罗列出部分点A 的横坐标由此可发现规律即的横坐标为：再结合已知即可得到答案【详解】观察发现规律：的横坐标为：的横坐标为：的横坐标为：的横坐标为：的横坐标为：故答案为：【点睛】本题 解析：2017201822π-【分析】根据点A 的取法，罗列出部分点A 的横坐标，由此可发现规律，即n A 的横坐标为：)12n -，再结合已知即可得到答案．【详解】观察，发现规律：1A 的横坐标为：1，2A 23A 的横坐标为：22，⋯，∴n A 的横坐标为：12n - n B ∴的横坐标为：12n -()()()404020192019201720182020452122223602S ππ⨯⨯∴=-⨯⨯=⋅-故答案为：2017201822π⋅-．【点睛】本题考查了一次函数图像上点的坐标特征以及规律型中的点的变换，解题关键是找出n A 的横坐标为：()12n -这一规律．14．【分析】连接ODBC 根据垂径定理和等腰三角形的性质得到DM=CM ∠COB=∠BOD 推出△BOD 是等边三角形得到∠BOC=60°根据扇形的面积公式即可得到结论【详解】解：连接ODBC ∵CD ⊥ABOC=解析：2π【分析】连接OD ，BC ，根据垂径定理和等腰三角形的性质得到DM=CM ，∠COB=∠BOD ，推出△BOD 是等边三角形，得到∠BOC=60°，根据扇形的面积公式即可得到结论．【详解】解：连接OD ，BC ，∵CD ⊥AB ，OC=OD ，∴DM=CM ，∠COB=∠BOD ，∵OC ∥BD ，∴∠COB=∠OBD ，∴∠BOD=∠OBD ，∴OD=DB ，∴△BOD 是等边三角形，∴∠BOD=60°，∴∠BOC=60°，∵DM=CM ，∴S △OBC =S △OBD ，∵OC ∥DB ，∴S △OBD =S △CBD ，∴S △OBC =S △DBC ，∴图中阴影部分的面积=260(23)π⨯=2π， 故答案为：2π．本题考查了垂径定理、扇形面积的计算，圆周角定理，正确添加辅助线是解题的关键． 15．【分析】根据二次函数表达式是易得新抛物线的顶点然后得到经过平移后的原抛物线的顶点根据平移不改变二次项的系数可得原抛物线解析式【详解】解：∵平移后抛物线的解析式是∴此抛物线的顶点为(14)∵向左平移3 解析：()226y x =++【分析】根据二次函数表达式是()214y x =-+易得新抛物线的顶点，然后得到经过平移后的原抛物线的顶点，根据平移不改变二次项的系数可得原抛物线解析式．【详解】解：∵平移后抛物线的解析式是()214y x =-+，∴此抛物线的顶点为(1，4)，∵向左平移3个单位，再向上平移2个单位可得原抛物线顶点，∴原抛物线顶点为(-2，6)，∴原抛物线的解析式是()226y x =++． 故答案为：()226y x =++．【点睛】本题考查了二次函数图象与性质，掌握二次函数图象的平移与坐标的变化规律是解题的关键． 16．①②④【分析】根据抛物线开口向下对称轴抛物线与轴相交于正半轴可得可以判断①和②正确；当时有解得由图像可知化简后可判断得③错误；由图像可知当时抛物线有最大值当时根据得到化简后得故④正确【详解】解：抛物解析：①②④．【分析】 根据抛物线开口向下，对称轴12b x a=-=-，抛物线与y 轴相交于正半轴，可得0a <，20b a =<，0c >，可以判断①和②正确；当0y =时，有210a x c a ，解得11a c x a ，21a c x a ，由图像可知，011a ca ，化简后可判断得③错误；由图像可知，当1x =-时，抛物线有最大值1y a b c ，当x m =时，22y am bm c ，根据12y y ≥得到20a b c am bm c 化简后得2am bm a b +≤-，故④正确．【详解】解：抛物线开口向下，抛物线的对称轴12b x a=-=-， 20b a ∴=<，抛物线与y 轴相交于正半轴，0c ∴>，∴0abc >，故①正确；∴2220a b a a -=-=，故②正确；当0y =时，2220ax bx c ax ax c ，∴210a x c a ∴11a c x a ， 21a c x a 由图像可知，011a c a ∴14a ca则有30a c +<，∴62320a c b c +=+<，故③错误；由图像可知，当1x =-时，抛物线有最大值1y a b c ， 当x m =时，22y am bm c ，∵12y y ≥∴20a b c am bm c 则2am bm a b +≤-，故④正确；故答案是：①②④．【点睛】本题考查了二次函数的图象与系数的关系，熟悉相关性质是解题的关键．17．【分析】利用配方法将原抛物线解析式化为顶点式【详解】解：y=x2-4x+5=x2-4x+4+1∴y=（x-2）2+1故答案是:【点睛】此题主要考查了配方法将二次函数一般式化为顶点式掌握配方法是关键解析：()221x -+【分析】利用配方法将原抛物线解析式化为顶点式，【详解】解： y=x 2-4x+5=x 2-4x+4+1，∴y=（x-2）2+1，故答案是: ()221x -+．【点睛】此题主要考查了配方法将二次函数一般式化为顶点式，掌握配方法是关键．18．6【分析】延长BF 交AD 的延长线于点H 证明△BCF ≌△HDF （AAS ）由全等三角形的性质得出BC ＝DH 由折叠的性质得出∠A ＝∠BGE ＝90°AE ＝EG 设AE ＝EG ＝x 则AD ＝BC ＝DH ＝3x 得出EH解析：66【分析】延长BF 交AD 的延长线于点H ，证明△BCF ≌△HDF （AAS ），由全等三角形的性质得出BC ＝DH ，由折叠的性质得出∠A ＝∠BGE ＝90°，AE ＝EG ，设AE ＝EG ＝x ，则AD ＝BC ＝DH ＝3x ，得出EH ＝5x ，由锐角三角函数的定义及勾股定理可得出答案．【详解】解：延长BF 交AD 的延长线于点H ，∵四边形ABCD 是矩形，∴AD ＝BC ，AD ∥BC ，∠A ＝∠BCF ＝90°，∴∠H ＝∠CBF ，在△BCF 和△HDF 中，CBF H BCF FDH CF DF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BCF ≌△HDF （AAS ），∴BC ＝DH ，∵将△ABE 沿BE 折叠后得到△GBE ，∴∠A ＝∠BGE ＝90°，AE ＝EG ，∴∠EGH ＝90°，∵AE ＝13AD ， ∴设AE ＝EG ＝x ，则AD ＝BC ＝DH ＝3x ，∴ED ＝2x ，∴EH ＝ED +DH ＝5x ，在Rt △EGH 中，sin ∠H ＝155EG x EH x ==， ∴sin ∠CBF ＝15CF BF =， ∴315BF =，∴BF ＝15，∴BC=故答案为：【点睛】本题考查了折叠的性质，矩形的性质，全等三角形的判定及性质，要注意折叠的图形中的相等的角和相等的线段，解题关键是利用倍长中线法正确作出辅助线证△BCF ≌△HDF ． 19．【分析】根据三角函数的性质一个锐角的正弦值等于它余角的余弦值可求【详解】解：∴故答案为：【点睛】本题考查了三角函数的性质解题关键是正确理解三角函数的意义得出一个锐角的正弦值等于它余角的余弦值 解析：513【分析】根据三角函数的性质一个锐角的正弦值等于它余角的余弦值可求．【详解】解：90C ∠=︒，5sin 13B =， ∴513=AC AB ， 5cos 13AC A AB ==, 故答案为：513． 【点睛】 本题考查了三角函数的性质，解题关键是正确理解三角函数的意义，得出一个锐角的正弦值等于它余角的余弦值．20．【分析】根据题意过点C 作CD ⊥AB 根据∠B ＝45°得CD ＝BD 根据勾股定理和BC ＝得出BD 再根据∠A ＝30°得出AD 进而分析计算得出AB 即可【详解】解；过点C 作CD ⊥AB 交AB 于D ∵∠B ＝45°∴C解析：3【分析】根据题意过点C 作CD ⊥AB ，根据∠B ＝45°，得CD ＝BD ，根据勾股定理和BC 得出BD ，再根据∠A ＝30°，得出AD ，进而分析计算得出AB 即可．【详解】解；过点C 作CD ⊥AB ，交AB 于D ．∵∠B ＝45°，∴CD ＝BD ，∵BC 6，∴BD 3∵∠A ＝30°，∴tan30°＝CD AD， ∴AD ＝30CD tan ︒33＝3， ∴AB ＝AD+BD ＝33． 故答案为：33．【点睛】本题考查解直角三角形，熟练应用三角函数的定义是解题的关键．21．（40+40）【分析】过A 作AQ ⊥BC 于Q ∠BAQ ＝60°∠CAQ ＝45°AB ＝80海里在直角三角形ABQ 中求出AQBQ 再在直角三角形AQC 中求出CQ 再根据BC ＝CQ+BQ 即可得出答案；【详解】解：解析：（3【分析】过A 作AQ ⊥BC 于Q ，∠BAQ ＝60°，∠CAQ ＝45°，AB ＝80海里，在直角三角形ABQ 中求出AQ 、BQ ，再在直角三角形AQC 中求出CQ ，再根据BC ＝CQ+BQ 即可得出答案；【详解】解：过A 作AQ ⊥BC 于Q ，由题意得：AB ＝80，在直角三角形ABQ 中，∠BAQ ＝60°，∴∠B ＝90°﹣60°＝30°，∴AQ ＝12AB ＝40，BQ 3＝3 在直角三角形AQC 中，∠CAQ ＝45°，∴CQ ＝AQ ＝40，∴BC ＝BQ+CQ ＝（3故答案为：（3【点睛】本题考查了解直角三角形的应用中的方向角问题、等腰直角三角形的性质、含30°角的直角三角形的性质等知识；通过解直角三角形得出CQ 和BQ 是解决问题的关键． 22．16【分析】先利用三角函数解直角三角形求得AC ＝20再根据勾股定理即可求解【详解】解：∵在直角三角形ABC 中∠B ＝90°cosA ＝AB ＝12∴cosA ＝＝＝∴AC ＝20∴BC ＝＝＝16故答案是：16解析：16【分析】先利用三角函数解直角三角形，求得AC ＝20，再根据勾股定理即可求解．【详解】解：∵在直角三角形ABC 中，∠B ＝90°，cosA ＝35，AB ＝12， ∴cosA ＝AB AC ＝12AC ＝35， ∴AC ＝20， ∴BC ＝22AC AB -＝222012-＝16．故答案是：16．【点睛】此题主要考查勾股定理、锐角三角函数的定义，正确理解锐角三角函数的定义是解题关键．三、解答题23．（1）画图见详解；（2）BC 扫过的面积S 圆环=9π=．【分析】（1）由三角板ABC 可求AB=2BC=6cm ，由勾股定理：2236933AB BC -=-=BC 在平面内绕顶点A 旋转一周．图形是以AB 为半径的圆去掉以AC 为半径的圆，所形成的圆环，如图所示；（2）BC 扫过的面积S 圆环=22AB AC ππ-计算即可．【详解】解：（1）∵三角板ABC ，90C ∠=︒，30A ∠=︒，3BC cm =，∴AB=2BC=6cm ，∴由勾股定理：AC=2236933AB BC -=-=，边BC 在平面内绕顶点A 旋转一周．图形是以AB 为半径的圆去掉以AC 为半径的圆，所形成的圆环，如图所示：（2）BC 扫过的面积S 圆环=2236279AB AC πππππ-=-=．【点睛】本题考查画旋转图形，勾股定理，30°直角三角形的性质，圆环面积，掌握画旋转图形方法，勾股定理，30°直角三角形的性质，圆环面积求法是解题关键．24．（1）5；（2）见解析；（3）262【分析】（1）根据垂等四边形的定义列式求解即可；（2）连结AC ，DB 并相交于点E ，证明AC BD ⊥，得到AOC △≌BOD ，证明AC BD =，即可得到结果；（3）方法一：连接DO ，AO ，根据已知条件求出AD ，DE ，再根据相似三角形的性质列式计算即可；方法二：通过已知条件证明Rt AOD 和Rt ABE △是等腰直角三角形，在根据条件计算即可；【详解】（1）由垂等四边形的定义得AC BD =，又∵AB AD ⊥，∴5cos AB DB ABD==∠， ∴5AC BD ==．（2）如图1，连结AC ，DB 并相交于点E ，∵OC OB ，OD OA ⊥，∴1452ACD AOD ∠=∠=︒，1452BDC BOC ∠=∠=︒， ∴90DEC ∠=︒，即AC BD ⊥，∵AO DO =，BO CO =，AOC DOB ∠=∠，∴AOC △≌BOD ，∴AC BD =．∵AC BD =，AC BD ⊥，∴四边形ABCD 是垂等四边形．（3）方法一：连接DO ，AO ，由（2）可得等腰Rt AOD ，∴24AD AO =-，作EF AD ⊥，易证得Rt DFE △∽Rt EFA △，∴2FE DF AF =⋅，设DF x =，4AF x =-，可得方程()43-=x x ，解得11x =（如图2），23x =（如图3），∴2DE =或23，作OG AB ⊥，∵12AOG AOB EDF ∠=∠=∠， ∴Rt DFE △∽Rt OGA ，∴AO AG DE EF=， ∴6AO EF AG DE ⋅==或2， ∴226AB AG ==（如图2）或22（如图3）．方法二：∵AC BD =且AC BD ⊥，∴AC BD =，∴AD BC =，∴()1180452ABE BAE AEB ∠=∠=︒-∠=︒， ∴90AOD ∠=︒，∴Rt AOD 和Rt ABE △是等腰直角三角形，∴4AD ==由方法一得2DE =或AE =AE =2，∴AB =【点睛】本题主要考查了圆的综合应用，结合相似三角形的判定与性质、三角函数的应用和四边形综合知识的计算是解题的关键．25．（1）-1；（2）若a ＞0，则y 1＜y 2；若a ＜0，则y 1＞y 2；（3）32a =【分析】（1）把A （4，0），B （-1，0）代入二次函数关系式求出a ，b 的值即可得到结果； （2）由点Q ，点N 的纵坐标相同，根据抛物线的对称性可得抛物线的对称轴，确定点P 距对称轴更近，分a ＞0和a ＜0两种情况讨论即可；（3）分别求出a +b =1，a-b-2=0，联立方程组求解即可．【详解】解：（1）∵二次函数y ＝ax 2+bx ﹣2（a≠0）的图像过A （4，0），B （-1，0）∴1642020a b a b +-=⎧⎨--=⎩解得，1=23=2a b ⎧⎪⎪⎨⎪-⎪⎩∴13122a b +=-=- （2）∵Q （m ，n ），N （3﹣m ，n ），∴二次函数图象的对称轴为3322m m +-= ∵P （1，y 1），M （3，y 2），∴点P 距离对称轴更近若a ＞0，则y 1＜y 2；若a ＜0，则y 1＞y 2； （3）由题意知，∵图像的顶点在第四象限，∴对称轴2b x a=-＞0 ∵B （﹣1，0），∴A 点横坐标大于1当x=1时，y=a+b-2＜0∴0＜a+b ＜2∵a+b为整数∴a+b=1又∵B（﹣1，0），∴a-b-2=0联立120 a ba b+=⎧⎨--=⎩解得，32 a=【点睛】本题为二次函数综合题，主要考查了待定系数法求函数的解析式，以及二次函数的性质．26．（1）点B的坐标是()1,3；（2）251366y x x=+；（3）1235=AB BS△．【分析】（1）过点A作AD x⊥轴于点D．过点B作BE x⊥轴于点E．证明()OEB AASADO≌△△，利用三角形全等的性质可得1OE AD==，3==BE OD，从而可得答案；（2）设过点A，O，B的抛物线的函数表达式为2y ax bx c=++，把()()()3,1,0,0,1,3,A O B-代入解析式，利用待定系数法列方程组解方程组可得答案；（3）如图，延长DA交1BB于,M由1,B B关于l对称，则1,DA BB⊥先求解抛物线的对称轴1313651026x=-=-⨯，1,B B关于l对称，再求解1,,BB AM利用三角形的面积公式可得答案．【详解】解（1）过点A作AD x⊥轴于点D．过点B作BE x⊥轴于点E．∴90,ADO BEO∠=∠=︒90AOD DAO∠+∠=︒，()3,1,A-3,1,OD AD ∴==∵90AOB ∠=︒，∴90AOD BOE ∠+∠=︒．∴DAO BOE ∠=∠．在Rt AOD 和Rt OBE 中，90ADO BEO DAO BOEAO BO ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴()OEB AAS ADO ≌△△．∴1OE AD ==，3==BE OD∴ 点B 的坐标是()1,3．（2）()()()3,1,0,0,1,3,A O B -设过点A ，O ，B 的抛物线的函数表达式为2y ax bx c =++，∴ 39310a b c a b c c ++=⎧⎪-+=⎨⎪=⎩． ∴561360a b c ⎧=⎪⎪⎪=⎨⎪=⎪⎪⎩． 过点A ，O ，B 的抛物线的函数表达式为251366y x x =+． （3）如图，延长DA 交1BB 于,M 由1,B B 关于l 对称，则1,DA BB ⊥251366y x x=+的对称轴1313651026x=-=-⨯．1,B B关于l对称，()()1,3,3,1,B A-1132321,105BB⎛⎫∴=⨯+=⎪⎝⎭()33M-，，312,AM∴=-=∴1123232255AB BS=⨯⨯=．【点睛】本题考查的是图形与坐标，三角形全等的判定与性质，利用待定系数法求解二次函数的解析式，二次函数的性质，掌握以上知识是解题的关键．。

卜人入州八九几市潮王学校天一实验2021届九年级数学下学期第一次模拟考试试题一、选择题〔本大题一一共10小题，每一小题3分，一共30分．在每一小题所给出的四个选项里面，只有一项为哪一项哪一项正确的，请需要用2B 铅笔把答题卡上相应的选项标号涂黑．．．．．．．．．．．．．〕 1．如右图，数轴上点A 所表示的数的相反数是(▲) A ．−2 B ．2C ．21D ．21-第1题图 2．以下运算中，正确的选项是(▲)A ．()b a ab 33=B ．1-=+--ba ba C ．326a a a =÷D ．222)(b a b a +=+3．函数51+=x y 中，自变量x 的取值范围是(▲)A ．5>xB ．x ≥−5C ．x ≤−5D ．x >−5 4．如图，所给图形中是中心对称图形但不是轴对称图形的是(▲) A ．B ．C ．D ．5．以下事件是确定事件的是(▲) A ．阴天一定会下雨B ．黑暗中从5把不同的钥匙中随意摸出一把，用它翻开了门C ．翻开电视机，任选一个频道，屏幕上正在播放新闻联播D ．在操场上向上抛出的篮球一定会下落6．数学活动课上，四位同学围绕作图问题：“如图，直线l 和l 外一点P ，用直 尺和圆规作直线PQ ，使PQ ⊥l 于点Q 〞．分别作出了以下四个图形，其中作法 错误的选项是(▲) 第6题图A ．B ．C ．D ．7．如图，点P 为平行四边形ABCD 的边AD 上的一点，E ，F 分别为PB ，PC 的中点，△PEF ，△PDC ，△PAB 的面积分别为S ，S 1，S 2．假设S =3，那么S 1+S 2的值是(▲)A ．24B ．12C ．6D ．3第7题图第9题图第10题图8．平面直角坐标系中，过点(−2，3)的直线l 经过一、二、三象限，假设点(0，a )，(−1，b )，(c ，−1)都在直线l 上，那么以下判断正确的选项是(▲)A ．a <bB ．a <3C ．b <3D ．c <−29．如图，在△AB C 中，AB =5，BC =3，AC =4，以点C 为圆心的圆与AB 相切，那么⊙O 的半径为(▲)A ．B ．C ．D ．10．如图，在菱形纸片ABCD 中，∠A =60°．将纸片折叠，点A 、D 分别落在点A′、D′处，且A′D′经过点B ，EF 为折痕．当D′F ⊥CD 时，FDCF的值是(▲)A ．813+ B ．63 C ．6132- D ．213- 二、填空题〔本大题一一共8小题，每一小题2分，一共16分，不需写出解答过程，只需把答案直接填写上在答题卡上相．．．．．应的位置．．．．〕 11．因式分解：2a 2−8a +8=▲．12．根据中国人社部统计2021年中国城镇新增长劳动力15000000人左右，总量压力巨 大，把15000000用科学记数法表示为▲．13．一组数据1，a ，3，6，7，它的平均数是4，这组数据的中位数是▲．14．一元二次方程0132=+-x x 的两根为x 1、x 2，那么x 1+x 2=▲．15．要制作一个圆锥模型，其侧面是由一个半径为3cm ，圆心角为150°的扇形纸板制成的，那么这个圆锥模型的侧面积为▲cm 2．16．反比例函数y =的图像经过点(2，3)，那么k 的值等于______▲____．17．如图，⊙O 是△ABC 的外接圆，连接OA ，OB ，∠OBA =48°，那么∠C 的度数为▲． 第17题图第18题图18．，正六边形ABCDEF 在直角坐标系内的位置如下列图，A (−2，0)，点B 在原点，把正六边形ABCDEF 沿x 轴正半轴作无滑动的连续翻转，每次翻转60°，经过2021次翻转之后，点B 的坐标是▲．三、解答题〔本大题一一共10小题，一共84分．请在答题卡指定区域内．．．．．．．．答题，解答时应写出文字说明、证明过程或者演算步骤〕19．(此题总分值是8分)计算：(1)计算：1)21(3)2(-+--+π(2)化简：121112--÷⎪⎭⎫ ⎝⎛--x x x 20．(此题总分值是8分) (1)解不等式组：(2)解方程：1223x x =+ 21．(此题总分值是7分)如图，正方形ABCD 中，点E 在对角线AC 上，连接EB 、ED ． (1)求证：△BCE ≌△DCE ；(2)延长BE 交AD 于点F ，假设∠DEB =140º，求∠AFE 的度数．22．(此题总分值是8分)区教育局为了丰富初生的大课间活动，要求各开展形式多样的阳光体育活动。

卜人入州八九几市潮王学校2021年九年级物理摸底试卷一、选择题〔每一小题3分，一共21分，以下各题的四个选项里面，只有一个选项是符合题目要求的．〕1．〔3分〕如下列图，在以下光现象中，说法正确的选项是〔〕A．日食是光的直线传播形成的B．黑板右端反光是由于光的漫反射形成的C．雨后彩虹是由于光的反射而形成的D．照相机形成的像是倒立、缩小的虚像2〔3分〕现代社会开展的三大支柱：能源、信息和材料，以下说法正确的选项是〔〕A．太阳能、风能、核能都是不可再生能源B．挪动通信是利用电磁波来传递信息的C．“北斗〞导航系统是利用超声波进展定位和导航的D．LED灯的核心元件发光二极管是由超导材料制成的3．〔3分〕以下热现象的解释中正确的选项是〔〕A．往皮肤上涂一些酒精会感到凉快﹣﹣﹣酒精蒸发时放热B．98℃的水也可沸腾﹣﹣﹣沸点随气压的升高而降低C．寒冷的北方室外多项选择用酒精温度计测温﹣﹣﹣酒精的凝固点低D．夏天，从冰箱里取出的易拉罐过一会儿外壁出现了小水滴﹣﹣﹣水蒸气凝华4．〔3分〕如下列图，以下说法中错误的选项是〔〕A．验电器检验物体是否带电B．小磁针转动，说明电流能产生磁场C．该实验能说明发电机的工作原理D．该实验用来研究电磁感应现象5．〔3分〕某班同学在“探究凸透镜成像规律〞的实验中，记录并绘制了像到凸透镜的间隔v跟物体到凸透镜的间隔u之间关系的图象，如下列图，以下判断正确的选项是〔〕A．该凸透镜的焦距是16cmB．当u=12cm时，在光屏上能得到一个缩小的像C．当u=20cm时成放大的像．投影仪就是根据这一原理制成的D．把物体从距凸透镜12cm处挪动到24cm处的过程中，像逐渐变小6．〔3分〕两个底面积不等的圆柱形容器〔S甲＜S乙〕，分别盛有甲、乙两种不同的液体，将两个完全一样的小球分别放入这两种液体中，小球静止时的位置如下列图，此时两液面刚好齐平．假设将这两小球从液体中取出，那么液体对容器底部压强的变化量△p甲、△p乙的大小关系是〔〕A．△p甲一定大于△p乙B．△p甲一定等于△p乙C．△p甲一定小于△p乙D．△p甲可能小于△p乙7〔3分〕小灯泡L的额定电压为3V，它的I﹣U图象如图甲所示．把小灯泡接入如图乙所示的电路中，先将滑动变阻器的滑片P移至B端，闭合开关S，电压表示数为V；再将滑片P向左挪动直到电压表示数为3V．电源电压恒定，滑动变阻器的铭牌标有“10Ω2A〞．以下说法中错误的选项是〔〕D．小灯泡正常发光时，滑动变阻器接入电路的阻值为3Ω二、、作图题〔一共11分〕8．〔2分〕某次测量如下列图，被测物体的长度是cm．9〔3分〕如下列图，一个小球从高处下落到竖直放置的弹簧上并压缩弹簧向下做减速运动，忽略空气阻力，画出小球所受的重力G和弹力f．10．〔3分〕请作出图中：①物体A所受重力G的示意图；②力F的力臂l．11．〔3分〕通电螺线管下方自由转动的小磁针静止后如下列图，请在图中标出螺线管的N、S极和螺线管中的电流方向．三、实验与探究题〔第12题6分，第13题7分．一共13分〕12〔6分〕结合国定义3月22日为国际水资源日，课外兴趣小组对我的供水系统和水质进展了如下实验测量．〔一〕测自来水的密度〔1〕某同学将天平放在程度桌面上，游码移到左侧的零刻度线，然后调节使指针指在分度标尺HY．内迅速〔填物态变化名称〕成高温、高压水蒸气，推动活塞再次做功，2〕正确操作，测出自来水和杯子总质量为，将局部水倒入量筒，如图甲所示，测出量筒中水的体积为cm3．测出剩余自来水和杯子的质量，如图乙所示，为g．〔3〕根据上述实验数据，计算自来水的密度为kg/m3．〔4〕在向量筒倒入自来水时，假设不慎有溅出，那么测出自来水的密度会〔选填“偏大〞、“偏小〞或者“不变〞〕．〔二〕测量水龙头翻开后的流量流量〔Q〕是单位时间是内通过横截面的体积，如图丙，水从B端流到A端所用时间是为t，水流速度为v，管内横截面积为S．根据流量的定义，Q=．〔要求用S、v、t中的字母表示〕．13．〔7分〕在“测量小灯泡电功率〞的实验中，电源电压恒为6V，小灯泡的额定电压为V，正常发光时灯丝电阻约为10Ω，所用滑动变阻器的最大阻值40Ω．〔1〕请用笔画线代替导线在图甲中完成实物电路的连接；〔2〕同学们进展试触时，发现小灯泡不发光，电流表无示数，电压表有示数，那么电路中发生的故障可能是〔选填“小灯泡断路〞、“小灯泡短路〞或者“滑动变阻器处断路〞〕；〔3〕某次实验中，同学们看到电压表示数为V，要使灯泡L正常发光应向〔选填“A〞或者“B〞〕端挪动滑片，同时视线应注意观察〔选填“电流表〞或者“电压表〞〕示数，当灯正常发光时，电流表示数如图乙所示，那么小灯泡的额定功率是W；〔4〕某同学还想探究电流与电阻的关系，于是将甲图中的小灯泡换成定值电阻R，并使电压表的示数始终保持2V不变，屡次更换阻值不同的定值电阻R，记录各次电流表的示数，在不更换其他器材的情况下，为了可以完成实验，他更换的定值电阻R的阻值不能大于Ω．14．〔7分〕0地震后灾后重建工作正在高效地进展，如图是某建筑工地上使用的塔式起重机．在一次操作过程中起重机将质量为500kg的建筑材料竖直提升了12m，用时15s，〔g=10N/kg〕．求：〔1〕所提建筑材料受到的重力；〔2〕起重机提起建筑材料所做的功；〔3〕提升过程中该起重机的电动机功率为8kW，那么提升过程中塔式起重机的机械效率是多大？15．〔7分〕如下列图，灯L标有“6V3W〞字样，电源电压恒为6V，定值电阻R=6Ω，设灯L的阻值不随温度变化而变化．求〔1〕灯L正常发光时的电阻是多少？〔2〕只闭合S1、S3时，电阻R在60s内产生的热量是多少？〔3〕要使整个电路消耗的电功率最小〔且电路电流不为0〕，各开关的合闭情况应如何？此时的最小电功率为多少？16．〔7分2014年4月14日，为寻找失联的MH370航班，启用了“蓝鳍金枪鱼﹣21”〔简称“金枪鱼〞〕自主水下航行器进展深海搜寻．其外形与潜艇相似〔如图甲所示〕，其相关参数为：体积1m3、重量7500N，最大潜水深度4500m，最大航速〔为简化计算，不考虑海水密度变化，海水密度ρ取1.0×103kg/m3，g取10N/kg〕．〔1〕假设“金枪鱼〞上有面积为2×10﹣3m2的探测窗口，当它下潜至4000m深度处时，该探测窗口承受海水的压力是多少？〔2〕“金枪鱼〞搜寻任务完成后，变为自重时，能静止漂浮在海面上，求此时“金枪鱼〞露出海面的体积为多大？〔3〕假设上述漂浮在海面的“金枪鱼〞，由起重装置将其匀速竖直吊离海面．从某时刻计时起，起重装置拉力的功率随时间是变化的图象如图乙所示，图中P3=3P1．请分析出t3时刻起重装置对“金枪鱼〞拉力，并求出t1时刻起重装置对“金枪鱼〞拉力〔不考虑水的阻力〕．。

A B C D九年级数学第一次模拟试题九年级数学(考试形式：闭卷 试题共五大题，25小题 卷面分数:120分 考试时限:120分钟)第一卷一．选择题（本大题共10小题，每小题3分，满分30分）每小题只有一个正确答案，请将选出的答案代号填入题后的括号内。

1．点A 在数轴上表示＋2，从点A 沿数轴向左平移3个单位到点B ，则点B 所表示的实数是（ ）。

A 、3B 、－1C 、5D 、－1或32．下列运算正确的是 （ ） A ． x 2＋x 2＝x 4 B ．(a －1)2＝a 2－1 C ．a 2·a 3＝a 5 D ．3x ＋2y ＝5xy3．如图， △ ABC 中，∠B = 90 º ，∠C = 30 º , AB = 1 ，将 △ ABC 绕顶点 A 旋转 1800 ，点 C 落在 C ′处，则 CC ′的长为 A . 42 B.4 C . 23 D . 253,()53525A. B. C. D. 5352a b aa b-==4.已知则5．一个不透明的袋中装有除颜色外均相同的5个红球和3个黄球，从中随机摸出一个，摸到黄球的概率是(A)18 (B) 13 (C) 38 (D) 356．在一个圆柱体中间挖出一个小圆洞，如图１所示，则该物体俯视图的形状是（ ）．7．顺次连接对角线相等的四边形各边的中点，得到一个四边形，对这个四边形的形状描述最准确的是（ ）A 、平行四边形B 、菱形C 、矩形D 、正方形8．教练组对运动员正式比赛前的5次训练成绩进行分析，判断谁的成绩更加稳定，一般需要考察这5 次成绩的（ ）．A ．平均数或中位数B ．众数或频率C ．方差或极差D ．频数或众数 9．已知⊙O 1的半径为3cm ，O 1到直线l 的距离为2cm ，则直线l 与⊙O 1的位置关系为（ ） A ．相交 B ．相切 C ．相离 D ．不相交 10．已知 k 1＜0＜k 2，则函数 y ＝k 1x 和 y ＝2k x的图象大致是（ ）A B C D二．填空题（本大题5小题，每小题3分，共15分）11．举世瞩目的长江三峡水利枢纽工程建成后，总装机容量为1820千瓦，年发电量为847亿千瓦时，将年发电量用科学记数法表示为 千瓦时。

一、初三物理欧姆定律易错压轴题（难）1．在探究“电压一定时，电流跟电阻的关系”的实验中，设计电路如图甲所示．（1）连接电路前，开关必须______．（2）请根据图甲电路图用笔画线代替导线将图乙所示实物连接成完整电路__（导线不允许交叉）．（3）连接好电路，闭合开关，发现电流表没有示数，移动滑动变阻器的滑片，电压表示数始终接近电源电压．造成这一现象的原因可能是______A．电流表坏了 B．滑动变阻器短路 C．电阻处接触不良 D．电阻短路（4）排除故障进行实验，多次改变R的阻值，调节滑动变阻器，使电压示数保持不变，实验数据记录如下表．其中第5次实验电流表示数如图丙所示，其读数为______A．（5）实验结果是：______．【答案】断开 C 0.12 电压不变，导体中的电流与导体的电阻成反比【解析】(1)连接电路前，为保护电路，开关必须断开；(2)电压表与电阻并联接入电路，滑动变阻器与电阻串联，采取“一上一下”的连接方式，如下图所示；(3)图丙中电流表用的是0.6A 量程，分度值为0.02A ，故其示数为0.12A ；(4)分析表格数据可知，电压一定时，通过电阻电流的变化倍数和电阻阻值变化倍数的倒数相等，故可得结论：电压不变，导体中的电流与其电阻成反比．点睛：根据电流表选用的量程和其分度值，读出电流表示数；分析表中电流的变化倍数和电阻的变化倍数之间的关系，利用控制变量法得出结论．2．小华为了探究“电流与电阻的关系”设计了如图甲所示的电路，其中电源电压恒为3V ，R x 的备选电阻有5Ω、10Ω、15Ω和20Ω各一个。

(1)闭合开关前滑动变阻器的滑片应置于______（选填“a ”或“b ”）端；试触时，发现电流表指针偏转到如图乙所示位置，说明电流表正、负接线柱______；(2)排除故障后，小华将5Ω的电阻接入电路中，移动滑片P 到某一位置，此时电流表的示数如图丙所示，电路中的电流为_______A ；(3)小华将10Ω的电阻替换5Ω的电阻接入电路中，闭合开关后，若不调节滑动变阻器，电压表示数会______（选填“变大”、“不变”或“变小”）；(4)小华依次把四个备选电阻接入电路，调节滑动变阻器，使电压表的示数为2V 不变，那么滑动变阻器接入电路的阻值变化范围是______Ω。

卜人入州八九几市潮王学校鹿邑县二零二零—二零二壹初三数学下期第一次模拟考试试卷一．选择题：〔本大题12个小题，每一小题4分，一共48分〕在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将正确答案的代号填入答题卷中对应的表格内．0，2，-3，-1中，最小的数是〔〕A.0B.2C.-3D.-12.下面计算正确的选项是〔〕A.B.C.D.3.以下汽车标志中，既是轴对称图形又是中心对称图形的是〔〕4.如图，，．那么等于〔〕A.B.C. D.5.要调查以下问题，你认为哪些适宜抽样调查〔〕①场上某种食品的某种添加剂的含量是否符合国家HY；②检测某地区空气的质量；③调查全生一天的学习时间是.A．①②B.①③C.②③D.①②③6.在Rt△ABC中，∠C=90°，AB=12，cosA=,那么AC等于〔〕A.36B.C.4D.7.某班进展乒乓球比赛，班主任教师为鼓励同学们积极参与，带了50元钱去购置甲、乙两种笔记本作为奖品.甲种笔记本每本7元，乙种笔记本每本5元，每种笔记本至少买3本，那么该教师购置笔记本的方案一共有〔〕A.3种B.4种C.5种D.6种8.如图，AB是⊙O的直径，∠AOC＝110°，那么∠D=()A．25°B．35°C．55°D．70°9.将函数变形为的形式，正确的选项是〔〕A．B．C．D．10.如图，爷爷从家〔点O〕出发，沿着扇形AOB上的途径去匀速漫步.设爷爷距家〔点O〕的间隔为s，漫步的时间是为t，那么以下列图形中能大致刻画s与t之间函数关系的图象是〔〕11.如图，是一组按照某种规律摆放而成的图案，那么图5中三角形的个数是〔〕．A.8B.9C.16D.1712.如图是二次函数图象的一局部，其对称轴为，且过点〔-3,0〕．以下说法：①；②；③；④3a+c=0；那么．其中说法正确的选项是〔〕．A.①②B.②③C.①②④D.②③④二、填空题：〔本大题6个小题，每一小题4分，一共24分〕请将每一小题之答案直接填在答题卡〔卷〕中对应的横线上。

九年级下册一模知识点九年级下册是初中学习生涯的最后一个学期，也是面临中考的阶段。

在这个时期，同学们需要复习和掌握九年级下册的各个知识点，以便在考试中取得好成绩。

下面是九年级下册一模考试的知识点总结。

语文九年级下册语文的重点是“阅读与表达”。

主要包括以下内容：1. 古文阅读：这是重点和难点，需要注意理解主旨、把握作者意图、推理等技巧。

2. 现代文阅读：要理解文章的结构和主题，把握语言的细节和修辞手法。

3. 口头表达和书面表达：要注意语言的准确性和流畅性，以及文章的组织结构和逻辑性。

数学九年级下册数学的知识点包括：1. 代数与函数：要熟练掌握一次函数的性质和图像，能够解一元一次方程和不等式，理解二次函数及其图像。

2. 几何与几何体：要能够解决平面图形的性质和计算问题，熟练掌握空间几何体的性质和计算方法。

3. 统计与概率：要能够计算和解决统计问题，理解概率的基本概念和计算方法。

英语九年级下册英语的知识点包括：1. 阅读理解：要能够理解并回答问题，根据文章推断主题和作者意图。

2. 语法：要掌握时态、语态、被动语态、虚拟语气等语法知识，确保语法的准确性。

3. 写作：要具备写作的基本技巧，能够写出连贯、准确和富有逻辑性的句子和段落。

物理九年级下册物理的主要知识点包括：1. 机械学：要掌握力的定义和计算，了解简单机械的原理和应用。

2. 光学：要理解光的传播规律和光的反射、折射现象，能够解答相关问题。

3. 电学：要掌握电的基本性质和电路的基本知识，理解电流、电压、电阻等概念。

化学九年级下册化学的主要知识点包括：1. 元素与化合物：要了解元素周期表和常见元素及其性质，理解化学式的表示方法和化合物的构成。

2. 化学方程式与化学反应：要掌握化学方程式的书写和平衡方法，理解化学反应的速率和热力学。

3. 酸碱与盐：要理解酸碱中和反应的原理，掌握常见酸碱的性质和应用。

历史九年级下册历史的知识点包括：1. 推背图与柔远堂：要了解中国古代的社会制度和政治组织形式，理解推背图和柔远堂的含义。