当前位置：文档之家 › 力的正交分解法

力的正交分解法

  • 格式：doc
  • 大小：113.50 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

【高中物理】力学：受力分析正交分解法

【高中物理】力学：受力分析正交分解法

【高中物理】力学：受力分析正交分解法【高中物理】力学：受力分析?正交分解法正交分解法是处理多个力作用问题的基本方法。

物体受到多个方向的外力作用均可使用正交分解法。

当对象受到多个力时，计算其合力，建立平面直角坐标系，并将对象上的每个力移动到平面坐标系的原点（公共点力）。

此时，每个力可以沿x轴和Y轴方向进行正交分解，然后分别沿这两个方向计算合力。

正交分解法是处理多力问题的基本方法。

值得注意的是，在选择方向时，尽可能使更多的力落在方向轴上；分解力尽可能已知。

运用条件当物体受到多个方向的外力时，可以使用正交分解法。

条件意义在求解多个公共点力的合成时，如果连续使用平行四边形规则，一般来说，应求解多个斜三角形，以反复求出部分合力的大小和方向。

计算过程非常复杂。

如果采用力正交分解法计算合力，计算过程更清晰。

它的基本思想是分解然后合成。

运用步骤第一步是直立并与X和Y坐标相交，这是最重要的一步。

X和Y坐标的建立不一定是水平和垂直的。

方向可以根据问题的方便程度设置，但X和Y方向必须相互垂直和正交。

第二步，将题目所给定跟要求的各矢量沿x、y方向分解，求出各分量，凡跟x、y轴方向一致的为正；凡与x、y轴反向为负，标以“一”号，凡跟轴垂直的矢量，该矢量在该轴上的分量为0，这是关键的一步。

第三步，根据各轴方向的运动状态方程，将矢量运算转化为标量运算；如果每个时间段的运动状态不同，则应根据每个时间段的状态分阶段建立方程。

这是这项法律的核心步骤。

第四步，根据各x、y轴的分量，求出该矢量的大小，一定要表明方向，这是最终的一步。

停留高中物理在学习中，正确应用正交分解法可以简化一些复杂问题，有效降低求解难度。

力的正交分解法在整个动力学中起着非常重要的作用。

注意在处理力的合成和分解时，我们通常沿着两个相互垂直的方向分解力。

这种方法称为力的正交分解法。

这是一种非常有用的方法。

使用时请注意以下几点：1.力是矢量f′在x轴y轴上的分矢量f′x和f′y是矢量，分量为正值表示分矢量的方向跟坐标轴的方向相同，分量为负值表示分矢量的方向跟坐标轴的方向相反。

正交分解法

正交分解法

班级： 姓名： 正交分解法解题什么是正交分解法——在分解合力时，如果两个分力的方向刚好垂直，则，可在两分力方向上建立直角坐标系，将力在正交的两条坐标上分解，所以叫正次分解法 正交分解法的步骤（1）：对研究对象正确的受力分析，并用力的图示准确的画出来正确分析受力就是要做到不添加力，不遗漏力要用好隔离法分析受力 准确的画图，是指用直尺按比例画好图，便于观察各力间的几何关系（2）：建立直角坐标系尽可能使较多的力在坐标轴上，这样不在坐标轴上的力就少，需要分解的力就少，使解题更方便（3）：将不在坐标轴上的力分解在坐标轴上，（平行四边行定则变成了矩形） （4）：根据图中的几何关系，利用三角函数或匀股定律求出各力的大小 附常用三角函数（sin=对边/斜边 cos=邻边/斜边）（sin300=21 cos300=23 ） （sin450=22 cos450=22 ） （sin600=23 cos600= 21 ） 练习：如图所示，一物体重20N ，置于水平地面上，一拉力作用于物体上，该拉力大小为10N ，且与水平方向夹角为300，物体在该拉力作用下匀速前进，求（1）：地面对物体的支持力的大小为多少？（2）：物体所受的摩擦力大小为多少？（3）：物体与地面间的动摩擦系数为多少？练习：1：气球受60N浮力悬于半空中（重力忽略），风从正东吹来。

气球随风倾斜，使拉气球的绳与地面夹角为600,求绳的拉力为多少？风吹气球的风力为多少？2：如图所示，一挡板垂直于斜面，将一重为30N的小球固定在了斜面上，求挡板对小球的支持力为多少？小球对斜面的压力为多少？3：如图一斜面倾角为450，物体与斜面间的动摩擦因数为 =0.2，一人用与斜面平行的力F将质量为2kg的物体匀速推上斜面，求推力F的大小为多少？。

正交分解法教案

正交分解法教案

正交分解法一、正交分解法把力按相互垂直的两个方向分解叫正交分解二、用力的正交分解求多个力的合力1、建立直角坐标系（让尽量多的力在坐标轴上）2、正交分解各力（将各力分解到两个坐标轴上）3、分别求出x 轴和y 轴上各力的合力：4、求出FX 和 Fy 的合力，即为多个力的合力大小： 方向：三、用力的正交分解求解物体平衡问题1、画出物体的受力图。

2、建立直角坐标系。

3、正交分解各力。

（将各力分解到两个坐标轴上）4、物体平衡时各方向上合力为零,分别写出x 方向 和y 方向方程。

22yx F F F +=x yF F =θtan ⎩⎨⎧==θθsin cos F F F F y x ⋅⋅⋅+++=xx x x F F F F 321⋅⋅⋅+++=y y y y F F F F 3215、根据方程求解。

例题2：如图所示，质量为m 的物体放在粗糙水平面上，它与水平面间的滑动摩擦因数为μ，在与水平面成θ角的斜向上的拉力F 作用下匀速向右运动。

求拉力F 的大小。

例题2：如图所示，质量为m 的物体放在粗糙水平面上，它与水平面间的滑动摩擦因数为μ，在与水平面成θ角的斜向上的拉力F 作用下匀速向右运动。

求拉力F 的大小。

∵物体匀速运动，合外力为零由x 方向合外力为零，有：由y 方向合外力为零，有：解得：例题3：如图所示，质量为m 的物体在倾角为θ的粗糙斜面下匀速下滑，求物体与斜面间的滑动摩擦因数。

θμθμsin cos +=mg F 0321=⋅⋅⋅+++=x x x x F F F F 0321=⋅⋅⋅+++=y y y y F F F F NF μθ=⨯cos mgF N =⨯+θsin解析：∵物体匀速运动，合外力为零由x 方向合外力为零，有：由y 方向合外力为零，有：解得：练习一：如图所示，质量为m 的光滑小球放在倾角为θ的斜面上被挡板挡住，求斜面对小球的弹力及挡板对小球的弹力。

θθθμtan cos sin ==Nmg μθ=⨯sin θcos mg N =练习二：如图所示，质量为m的物体在与竖直方向成θ角的恒力F作用下沿粗糙墙面向上匀速运动，求物体与墙壁间的动摩擦因数。

3.5力的分解(作用效果、正交、矢量相加、三角形)

3.5力的分解(作用效果、正交、矢量相加、三角形)

按照实际的作用效果，确定分力的方向。

按照这两个力的方向做平行四边形。

再根据数学几何关系，求出两个分力。

F 1
F 2
F θ
θ
G
G
θ1
F 2
F
G
1
F 2
F θ
1
F 2F θ
G
F
1
F
2
θ
G
质量为m的木块，在拉力F的作用下在水平地面上做匀速运动，
已知木块与地面间的动摩擦因数为u,则木块受到的滑动摩擦力为？
F
θ
正确选择直角坐标系，以此代表分力的方向按照平行四边形定则，做平行四边形再根据数学几何关系，求出两个分力。

︒
120N
F 1251=N
F 3752=N F 3503=︒
90
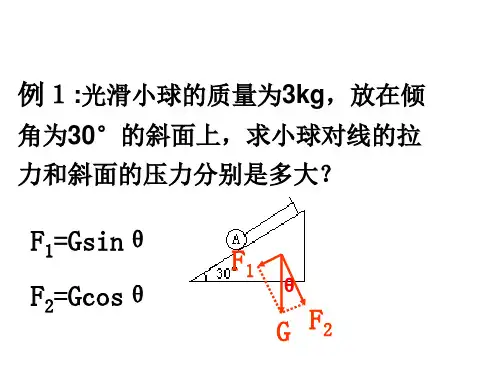
重力为G的物体静止在斜面上，求静摩擦力的大小？如果该物体在斜面上匀速向下滑动，
求滑动摩擦力的大小？（动摩擦因数为u）θ
三、矢量相加法则
任何矢量相加时
都满足平行四边形定则
四、三角形定则
把两个矢量首尾连接
从而求出合矢量，叫做三角形定则三角形定则的本质是平行四边形定则3N
1N
5N
2N
1N
2N2N
5N5N
1N
3N。

力的正交分解法1

力的正交分解法1
求合力。
y
F3
F2
600
O
F1
o
x
小结：
• 正交分解法： • （1）方法：把力沿经选定的两个相互垂直的方向分解。
Y
FY
F合
O
Fx X
（2）目的：将力的合成化简为同向或反向
或垂直方向。便于运用普通代数运算公式来
解决矢量的运算。
（3）步骤： 1.正确选定直角坐标系。 2.分别将各力投影到坐标轴上。 3.求各力的分力在Ｘ，Ｙ轴的合力。 4.再求合力的大小和方向。 计算：
作业：
Fx合=F1x+F2x+F3x+…
Fy合=F1y+F2y+F3y+…
F合= Fx合2+ Fy合2 tan θ= Fy合/ Fx合
课例1：重为100N的物块，放在倾角为300光滑 斜面上，求斜面受到正压力和使物块下滑的分 力大小。
变式 ：重为100N的物块，放在倾角300的斜面 上，物块匀速下滑，求物块受到的摩擦力大小。
力的正交分解法
F2
F
θ
F1
G1
G2 G
从上面两图中可以发现，我们按照力的作用效果把F 和G进行分解所得到的两个分力的方向是相互垂直的， 这种分解力的方法叫做力的正交分解法。
问题：为什么要提出力的正交分解法？
问题讨论Байду номын сангаас
F3
F2
与 与 O F • 1、大小均为F的三个力共同作用在O点，如图F1 F2、F2 F3之间夹角均为600， 1
N=G1=G·COS Ф F=G2= G·SinФ
G2
Ф
G1
G
课例2：如图所示，水平地 面上的重为150N木块，受

高中物理必修一人教版课件：第三章之受力分析 正交分解法 (共10张PPT)

高中物理必修一人教版课件：第三章之受力分析 正交分解法 (共10张PPT)
选择合适的坐标 分解不在坐标上的力 进行同轴的代数和的运算 将两个垂直的力合成
10-10
6、“教学的艺术不在于传授本领，而在于激励、唤醒、鼓舞”。2021年11月2021/11/222021/11/222021/11/2211/22/2021
•7、不能把小孩子的精神世界变成单纯学习知识。如果我们力求使儿童的全部精神力量都专注到功课上去，他的生活就会变得不堪忍 受。他不仅应该是一个学生，而且首先应该是一个有多方面兴趣、要求和愿望的人。2021/11/222021/11/22November 22, 2021
10-05
正交分解法
10-06
•1、所有高尚教育的课程表里都不能没有各种形式的跳舞：用脚跳舞，用思想跳舞，用言语跳舞，不用说，还需用笔跳舞。 •2、一切真理要由学生自己获得，或由他们重新发现，至少由他们重建。 •3、教育始于母亲膝下，孩童耳听一言一语，均影响其性格的形成。 •4、好的教师是让学生发现真理，而不只是传授知识。 •5、数学教学要“淡化形式，注重实质.
•8、教育技巧的全部诀窍就在于抓住儿童的这种上进心，这种道德上的自勉。要是儿童自己不求上进，不知自勉，任何教育者就都不 能在他的身上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方，儿童才会产生上进心。 2021/11/222021/11/222021/11/222021/11/22
正交分解法
10-01
力的合成和分解
10-02
正交分解法
正交——相互垂直的两个坐标轴
选择一个坐标轴，将力分解为两个轴上的相互垂直的分力
FX= Fcosα
y
Fy
F
Fy= x
10-03
正交分解法
例：确定正六边形内五个力的合力

(最新整理)高一物理力的分解正交分解法

(最新整理)高一物理力的分解正交分解法

例2.三个力共同作用在O点，如图2所示，F1、F2与F3 大小相等均 为Ｆ，他们之间的夹角均为600，求合力。
例3.如图3所示，用绳AO和BO吊起一个重100N的物体，两绳AO、
BO与竖直方向的夹角分别为30o和45o，求绳AO和BO对物体的拉力
的大小。
A
F3
F2
B
300
30o
45o
图1
2021/7/26
(最新整理)高一物理力的分解正交分解法
2021/7/26
1
力的分解
正交分解法
2021/7/26
2
四、力的正交分解
在很多问题中，常把一个力分解为 互相垂直的两个分力，特别是物体受 多都个分力解作到F用互2 时相，垂把直物的体两受个到方F1的向各上个去力， 然后求两个方向上的力的合力，这样 可把复杂问题简化，尤其是在求多个 力的合力时，用正交分F3解的方法，先 将力分解再合成非常简单．
F Fx2 Fy2
4
例：三个力F1、F2与F3 共同作用在O点。如图,
该如何正交分解？yຫໍສະໝຸດ F2F1y F2y
F1
F2X
O
F3y
F3x F1x
x
F3
怎样去选取坐标呢？原则上是任意的，实际 问题中，让尽可能多的力落在这个方向上， 这样就可以尽可能少分解力．
2021/7/26
5
例1.物体放在粗糙的水平地面上，物体重50N，受到斜向上方向与 水平面成300角的力F作用，F = 50N，物体仍然静止在地面上， 如图1所示，求：物体受到的摩擦力和地面的支持力分别是多少？
图2
F1
O
G
图3
6
例4.质量为m的物体在恒力F作用下，F与水平方向之间的夹角为θ, 沿天花板向右做匀速运动，物体与顶板间动摩擦因数为μ，则物体 受摩擦力大小为多少？

正交分解法

正交分解法

• 如图，物体重力为10N，AO绳与顶板间的夹角为45º ， BO绳水平，试用计算法求出AO绳和BO绳所受拉力的 大小。
y
FAOY=FAOcos45=G
A FAO FAOX O
FAOY B x
FAOX=FBO=G
C
• 如图，氢气球被水平吹来的风吹成图示的情形，若 测得绳子与水平面的夹角为37˚，已知气球受到空气 的浮力为15N，忽略氢气球的重力，求： • ①氢气球受到的水平风力多大？ • ②绳子对氢气球的拉力多大？
F3
例2:光滑小球的质量为3kg，放在倾 角为30°的斜面上，求小球对线的拉 力和斜面的压力分别是多大？ y x Gx=Gsinθ=T N o T Gx Gy=Gcosθ=N Gy
G
例3:质量为3kg的物体A悬挂在水平
支架上，悬线与竖直墙壁的夹角为 60°，悬绳受到的拉力和轻杆受到 的压力分别是多大？
一、定义：
把物体受到的各个力沿两个选定 的互相垂直的方向分解，叫力的正交 分解法
1、说明：正交分解法是一种很有用的方法， 尤其适合于三个或三个以上共点力作用的 情况。 2、优点：化“矢量运算”为“代数运 算”。
二、利用正交分解法解题的一般步骤1：
1、对物体进行受力分析； 2、建立直角坐标系xoy；
建立原则： ａ、沿物体的运动方向和垂直于物体的 运动方向； ｂ、沿力的方向，使尽量多的力在坐标轴上； C、通常选共点力的作用点为坐标原点。
二、利用正交分解法解题的一般步骤2：
3、分别将不在坐标轴上的力投影到坐标 轴上； 4、用代数运算法分别求出所有在x轴方向 和y轴方向上的投影合力∑Fx 和∑Fy ；
其中， ∑Fx = Fx1 +Fx2+ Fx3+„„ ∑Fy = Fy1+Fy2+ Fy3+„„

力的正交分解法2(人教版)

力的正交分解法2(人教版)
例１:光滑小球的质量为3kg，放在倾
角为30°的斜面上，求小球对线的拉 力和斜面的压力分别是多大？
F1=Gsinθ F2=Gcosθ
F1
θ
G F2
例２:质量为3kg的物体A悬挂在水
平支架上，悬线与竖直墙壁的夹角
为60°，悬绳受到的拉力和轻杆 受到的压力分别是多大？
F2
F
F1
正交分解法
把物体受到的各个力沿两个选定的互相 垂直的方向分解，叫力的正交分解法
例5:如图所示，用细线OA、OB悬一重物，
OA和OB与天花板的夹角分别θ1＝30°和 θ2＝60°，它们所能承受的最大拉力分别 为F1＝1000N和F2＝1500N， 求悬挂物的最大重力.
y
F2 FF12yy
F1
F2X o F1X
x
F3
利用正交分解法解题的的一般步骤：
1、分析物体的受力情况； 2、建立直角坐标系； 建立原则： ａ、沿尽量多的力在坐标轴上。
3、根据物体沿ｘ轴或ｙ轴的所处的状态 列方程求解。
例１:光滑小球的质量为3kg，放在倾角 为30°的斜面上，求小球对线的拉力和 斜面的压力分别是多大？
说明：正交分解法是一种很有用的方法， 尤其合适于三个或三个以上共点力 作用的情况。
基本思路：将各力分解到选定的坐标方向 上去，根据要求列式求解。
优点： 化“矢量运算”为“代数运 算”。
例3：如图所示，物体受到F1、F2和F3的作用，
F2与F3的夹角为1350 ，F1与F3的夹角为1500， 其中F3=10N，物体处于静止状态，则F1和F2的 大小个为多少？
y
x
No Gx
T
Gx=Gsin θ=T
Gy
Gy=Gcos θ=N

高中物理必修一 正交分解法

高中物理必修一 正交分解法
如图a建立直角坐标系，把各个力分解到 两个坐标轴上，并求出x轴y轴上的合力 Fx和Fy，有 Fx＝F1＋F2cos 37° －F3cos 37° ＝27 N Fy＝F2sin 37° ＋F3sin 37° －F4＝27 N
因此，如上图 b 所示，合力 F＝ F2x＋Fy2≈38.2 N tan φ＝FFxy＝1 所以 φ＝45°.
力的正交分解法
1.正交分解法求合力
概念： 将力沿着两个选定的相互垂直的方向分解 优点： 把矢量运算转化为代数运算 适用情况： 适用于计算三个或三个以上力的合成
例1
解析：本题若连续运用平行四边形定则求解，需 解多个斜三角形，一次又一次确定部分合力的大 小和方向，计算过程十分复杂．为此，可采用力 的正交分解法求解此题．
【解析】先对物体进行受力分析，如右图所示，
然后对力F进行正交分解． 水平方向分力F1＝Fcosθ 竖直方向分力F2＝Fsinθ 由力的平衡可得
F1＝f，F2＝mg＋N 又由滑动摩擦力公式知f＝μN 将F1和F2代入可得f＝Fcosθ＝μ(Fsinθ－mg)， 故正确选项为B、C. 【答案】 BC
Fx＝F1x＋F2x＋…
Fy＝F1y＋F2y＋…
(5)求共点力的合力，合力大小F＝ Fx2＋Fy2，
合力的方向与x轴的夹角为α，则tan α＝ FFyx.
2.共点力作用下物体的平衡的基本分析方法
(1)合成法
(2)分解法
(3)正交分解法
例2 如图所示，重为G的 物体放在水平面上，推力 F与水平面夹角为θ，物体 做匀速直线运动，已知物 体与地面间的动摩擦因数 为μ，求施加的推力F和物 体所受的摩擦力。
代入数据得：
F
G
cos sin
FN

牛二定律中正交分解、整体隔离法

牛二定律中正交分解、整体隔离法
解题步骤 1、画出物体的受力图 2、建立直角坐标系 3、正交分解各力 4、别写出x、y方向的方程 5、根据方程求解
F θ
例题1：如图所示，质量为m的物体放在粗糙水 平面上，它与水平面间的滑动摩擦因数为μ， 在与水平面成θ角的斜向上的拉力F作用下匀 速向右运动。求拉力F的大小。
y
N f θ F 物体匀速运动，合外力为零 由x方向：
3.将不在坐标轴的力投影到X、Y轴上 4．根据物体沿ｘ轴或ｙ轴的所处的状态 列方程： Fx合=F +F +F +……= ma Fy合=F +F +F +……=0
1x 2x 3x 1y 2y 3y
5、根据方程求解
牛顿第二定律中的
连结体问题：
1、连结体：两个(或两个以上)物体相 互连结参与运动的系统。
3.如图所示,在光滑的地面上,水平外力F拉 动小车和木块一起做加速运动,小车质量为 M,木块质量为m,设加速度大小为a,木块和 小车之间的动摩擦因数为µ ,则在这个过程 中,木块受到的摩擦力大小是:
A,µmg
C,mF/(M+m)
B.ma
D,F-Ma
m M
a F
牛顿第二定律中的
பைடு நூலகம்
力的正交分解
定义：把力沿着两个选定的互相垂直的方向分解
正交——相互垂直的两个坐标轴
y
Fy
F
θ
Fx
O
Fx F cos Fy F sin
x
例题1：如图所示，质量为m的物体放在粗糙水 平面上，它与水平面间的滑动摩擦因数为μ， 在与水平面成θ角的斜向上的拉力F作用下匀 速向右运动。求拉力F的大小。
例1:光滑的水平面上有质量分别为m1、m2的 两物体 静止靠在一起(如图) ,现对m1施加 一个大小为 F 方向向右的推力作用。求此 时m2和 m1之间的作用力

高一物理正交分解法ppt课件

高一物理正交分解法ppt课件

0下载券文档一键搜索 VIP用户可在搜索时使用专有高级功能：一键搜索0下载券文档，下载券不够用不再有压力！
内容特 无限次复制特权 权 文档格式转换
知识影响格局，格局决定命运！ VIP有效期内可以无限次复制文档内容，不用下载即可获取文档内容
VIP有效期内可以将PDF文档转换成word或ppt格式，一键转换，轻松编辑！
Fy
F2
Fx F1x F2x Fnx
Fy F1y F2y Fny
F合 (Fx )2 (Fy )2
θ F2x
F合
Fx
x
特权福利
特权说明
VIP用户有效期内可使用VIP专享文档下载特权下载或阅读完成VIP专享文档（部分VIP专享文档由于上传者设置不可下载只能 阅读全文），每下载/读完一篇VIP专享文档消耗一个VIP专享文档下载特权。
包权
人书友圈7.三端同步
注意：若F=0，则可推出得Fx=0，Fy=0，这是处 理多个力作用下物体平衡问题的好办法，以后常 常用到。
（物体的平衡状态指：静止状态或匀速直线运动 状态）
正交分解法
例：确定正六边形内五个力的合力
y
y
F1y F1
F2
F1y F2y
0
F1x
F5x
x
F3
0
F1x F5x
F2x
F A
y FN
Fcosα
α x
Ff Gsinα
F Fsinα
Gcosα G
练习4.
用与竖直方向成θ=37°斜向右上方，大小为 F=200N的推力把一个质量m=10kg的木块压在粗
糙竖直墙壁上正好向上做匀速运动。求墙壁对 木块的弹力大小和墙壁与木块间的动摩擦因数。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题一：物体的受力分析
（一）物体的受力分析
物体之所以处于不同的运动状态，是由于它们的受力情况不同。

要研究物体的运动，必须分析物体的受力情况。

正确分析物体的受力情况，是研究力学问题的关键，是必须掌握的基本功。

如何分析物体的受力情况呢？主要依据力的概念，从物体所处的环境（有多少个物体接触）和运动状态着手，分析它与所处环境的其他物体的相互联系。

具体的分析方法是：
1、确定所研究的物体，然后找出周围有哪些物体对它产生作用。

不要找该物体施于其他物体的力。

比如所研究的物体叫A，那么就应该找出“甲对A”和“乙对A”及“丙对A”的力……而“A对甲”或“A对乙”等力就不是A所受的力。

也不要把作用在其他物体上的力错误地认为通过“力的传递”作用在研究对象上。

2、要养成按步骤分析的习惯。

先画重力：作用点画在物体的重心。

其次画接触力（弹力和摩擦力）：绕研究对象逆时针（或顺时针）观察一周，看研究对象跟其他物体有几个接触点（面），某个接触点（面）若有挤压，则画出弹力，若还有相对运动或趋势，则画出摩擦力。

分析完这个接触点（面）后再依次分析其他接触点（面）。

再画其他场力：看是否有电场、磁场作用，如有则画出场力。

3、画完受力图后再作一番检查。

检查一下画出的每个力能否找出它的施力物体，若没有施力物体，则该力一定不存在。

特别是检查一下分析的结果，能否使研究对象处于题目所给的运动状态，否则必然发生了多力或漏力的现象。

4、如果一个力的方向难以确定，可用假设法分析。

先假设此力不存在，观察所研究的物体会发生怎样的运动，然后审查这个力应在什么方向时，研究对象才能满足给定的运动状态。

5、合力和分力不能重复地列为物体所受的力。

力的合成与分解的过程是合力与分力“等效替代”的过程，合力和分力不能同时存在。

在分析物体受力情况时，如果已考虑了某个力，那么就不能再考虑它的分力。

例如，在分析斜面上物体的受力情况时，就不能把物体所受重力和“下滑力”并列为物体所受的力，因为“下滑力”是物体所受重力在沿斜面方向上的一个分力。

专题二：力的正交分解法
1、定义：把力沿着两个选定的互相垂直的方向分解，叫做力的正交分解法。

说明：正交分解法是一种很有用的方法，尤其适于物体受三个或三个以上的共点力作用的情怳。

2、正交分解的原理
一条直线上的两个或两个以上的力，其合力可由代数运算求得。

当物体受到多个力的作
用，并且这几个力只共面不共线时，其合力用平行四边形定则求解很不方便。

为此，我们建立一个直角坐标系，先将各力正交分解在两条互相垂直的坐标轴上，分别求出两个不同方向
上的合力F x和F y，然后就可以由F合=，求合力了。

说明：“分”的目的是为了更方便的“合”
正交分解法的步骤：
（1）以力的作用点为原点作直角坐标系，标出x轴和y轴，如果这时物体处于平衡状态，则两轴的方向可根据方便自己选择。

（2）将与坐标轴不重合的力分解成x轴方向和y轴方向的两个分力，并在图上标明，用符号F x和F y表示。

（3）在图上标出力与x轴或力与y轴的夹角，然后列出F x、F y的数学表达式。

如：F 与x轴夹角为θ，则F x=Fcosθ，F y=Fsinθ。

与两轴重合的力就不需要分解了。

（4）列出x轴方向上的各分力的合力和y轴方向上的各分力的合力的两个方程，然后再求解。

【典型例题】
例1、如图所示，用绳AC和BC吊起一个重100N的物体，两绳AC、BC与竖直方向的夹角分别为30°和45°。

求：绳AC和BC对物体的拉力的大小。

解：此题可以用平行四边形定则求解，但因其夹角不是特殊角，计算麻烦，如果改用正交分解法计算简便得多。

先以C为原点作直角坐标系，设x轴水平，y轴竖直，在图上标
出F AC和F BC在x轴和y轴上的分力。

即：
F ACx=F AC sin30°=F AC F ACy=F AC cos30°=F AC
F BCx=F BC sin45°=F BC F BCy=F BC cos45°=F BC
在x轴上，F ACx F BCx大小相等即F AC=F BC （1）在y轴上，F ACy与F BCy的合力与重力相等
即F AC+F BC=100 （2）
解（1）（2）得绳BC的拉力F BC=25（－）N=25（－1）N
绳AC的拉力F AC=50（－1）N
例2、如图所示，重力为500N的人通过跨过定滑轮的轻绳牵引重200N的物体，当绳与水平面成60°角时，物体静止。

不计滑轮与绳的摩擦，求地面对人的支持力和摩擦力。

分析：人和重物静止，所受合力皆为零，对物分析得到，绳拉力F等于物重200N；人受四个力作用，将绳的拉力分解，即可求解。

解：如图所示，将绳的拉力分解得
水平分力F x=Fcos60°=200×N=100N
竖直分力F y=Fsin60°=200×N =100N
在x轴上，F′与F x二力平衡所以静摩擦力F′=F x =100N
在y轴上，三力平衡得地面对人支持力
F N=G－F y=（500－100）N=100（5－）N
例3、如图所示：将重力为G的光滑圆球用细绳拴在竖直墙壁上，如图，当把绳的长度增长，则绳对球的拉力T和墙对球的弹力N是增大还是减小。

图（a）
解：根据球的平衡条件=0用已知力G求未知力T、N。

（1）明确对象，作受力分析，如图（a），球受G、N、T，设绳与墙夹角为θ。

（2）选用方法：
A、合成法：因为=0。

所以任意两个力的合力均与第三个力大小相等，方向相反。

如图（b），N、G合力T?，T?=T根据平行四边形法则，则在
图（b）图（c）
B、分解法：因为=0。

所以其中任一个力在其它两个力方向的分力均与该力大小相等、方向相反而平衡。

如图（c），在T、N方向上分解G有T?=T，N?=N。

仍可看。

C、用正交分解法：建立直角坐标系。

如图（d），因为球受=0，必同时满足
，。

对三种解法要深刻理解，针对具体问题灵活运用，讨论结果：。