受力分析 正交分解法PPT课件

矢量的运算。
步骤
1、先对物体进行受力分析，画出受力示意图。 2、以力的作用点为坐标原点，恰当地建立直角坐 标系，标出x轴和y轴。 注意：坐标轴方向的选择虽具有任意性， 但原则是：使坐标轴与尽量多的力重合， 使需要分解的力尽量少和容易分解。 3、将不在坐标轴上的各力分解为沿两坐标轴方向 的分力，并在图上标明。
F3x
F1x
O
F3y
x
F
F
y
x
F1 F2 x F3x ...
F3 y
ΣF
F1y F2 y F3 y ...
ΣFy
2 2 F F x y
F
tan
Fy Fx
O
ΣFx
x
目的：
是化复杂的矢量运算为普通的代数运
算，将力的合成化简为同向或反向或垂直
方向。便于运用普通代数运算公式来解决
1．如图所示，用绳AO和BO吊起一个重 100N的物体，两绳AO、BO与竖直方向 的夹角分别为30o和45o，求绳AO和BO对 物体的拉力的大小。
2. 如图所θ＝370，sin370＝0.6 cos370 ＝0.8。箱子重G＝200N，箱子与地面的 动摩擦因数μ＝0.30。要匀速拉动箱子， 拉力F为多大？
Ff=μ FN
Ff Gsinα
Fcosα F Fsinα G Gcosα
x
例1：一个物体受到四个力的作用，已知
F1=1N，方向正东；F2=2N，方向东偏北 600，F3= 3 3 N，方向西偏北300；F4=4N， 方向东偏南600，求物体所受的合力。
y
F3 F2y
300
F3y F2
600
2x
F4x
A FAO FAOX O y FAOY B

优质课件优秀课件课件公开课免费课 件下载 免费ppt 下载人 教版（ 2019） 高中物 理必修 第一册 物理必 精通的 正交分 解法（ 共14张 PPT）
注意：若F=0，则可推出得Fx=0，Fy=0，这是处 理多个力作用下物体平衡问题的好办法，以后常 常用到。 （物体的平衡状态指：静止状态或匀速直线运动 状态）
又 Ff F N ③
mg
由②得： FN mg F sin 由①②③有： F cos mg F sin
优质课件优秀课件课件公开课免费课 件下载 免费ppt 下载人 教版（ 2019） 高中物 理必修 第一册 物理必 精通的 正交分 解法（ 共14张 PPT）
B. (mg+Fsin) C. (mg-Fsin) D. Fcos
Ff
F2 x
mg
F1
F
为了求合力进行正交分解，分解是方法，合 成是目的。
优质课件优秀课件课件公开课免费课 件下载 免费ppt 下载人 教版（ 2019） 高中物 理必修 第一册 物理必 精通的 正交分 解法（ 共14张 PPT）
优质课件优秀课件课件公开课免费课 件下载 免费ppt 下载人 教版（ 2019） 高中物 理必修 第一册 物理必 精通的 正交分 解法（ 共14张 PPT）
正交分解法
例1、如图，物体重力为10N，AO绳与顶板间的夹角为45º， BO绳水平，试用计算法求出AO绳和BO绳所受拉力的大小。
FAX=FAsin45°=FB
FAY=FAcos45°=G
FB 2G
FA G
y
A FA
FAY
FAX O
Bx FB
CG
优质课件优秀课件课件公开课免费课 件下载 免费ppt 下载人 教版（ 2019） 高中物 理必修 第一册 物理必 精通的 正交分 解法（ 共14张 PPT）

y
x
FN
Ff
Ff G sin
G1

G2
FN G cos
θ
G
NEXT

第五节
力的分解
4、正交分解法
（2）练习1：用绳AC和BC吊起一个重100N的物体，两绳AC、 BC与竖直方向的夹角分别为30o和45o，求：绳子AC和BC对物体 的拉力分别为多少？P70《名师一号》 FAC 50 ( 3 1) N
NEXT

第五节
力的分解
5、物体动态平衡问题
（1）例题：球重为G，求绳子拉力和墙壁的支持力，并求当绳子 变短时，这两个力如何变化？

FT G
FN G tan
FT
FN
G cos
G
NEXT

第五节
力的分解
5、物体动态平衡问题
（2）练习1：
θ
NEXT

第五节
力的分解
5、物体动态平衡问题
例题1.把一个物体放在倾角为θ 的斜面上，物体并没有在 重力作用下竖直下落，从力的作用效果看，应怎样将重力分解 ？两个分力的大小与倾角有什么关系？
G1
sin
G1 G1 G sin G G2 G2 G cos G

G
G2
cos
NEXT

第五节
力的分解
2、具体实例
• （3） 已知一个力(合力)和一个分力的方 向, 另一个分力有无数解，且具有最小 值。
F1
O
F
F2
3、已知合力和两个分力的大小
两组解
（F1+F2>F且F1≠F2)
合力一定,两等大分力随它们之间 的夹角变化而如何变化?

例题7：质量为m的物体放在倾角为θ的斜面上，在 平行斜面的推力的作用下，物体沿斜面匀速 运动。物体与斜面的动摩擦因数为μ
1）若向上运动，求：推力的大小______ 斜面对物体支持力的大小______
2）若向下运动，求：推力的大小________ 斜面对物体支持力的大小________
F
θ
人 教 版 高 一 物理必 修一： 3.5 力 的 分解 ——正 交分解 法(共2 0张PPT )【PPT 优秀课 件】-精 美版
正交分解法
学会正交分解法求合力 解决复杂平衡问题
问题：将F力向如图所示方向分解， 求分力大小容易么？
60°
F
45°
问题：求F1、F2的合力容易么？
F2=25N
30°
F1=40N
问题：将F力向如图所示方向分解， 求分力大小容易么？
已知F=100N,两分力的方向互相垂直，如图 求出：两个分力的大小
人 教 版 高 一 物理必 修一： 3.5 力 的 分解 ——正 交分解 法(共2 0张PPT )【PPT 优秀课 件】-精 美版
例四 质量为m的物体沿粗糙斜面匀速下滑， 斜面倾角为α， 求：物体受到的支持力和摩擦力 物体与斜面的动摩擦因数多大？
f
N
物体匀速运动，合力为零 X轴方向：f=mgsin α---1）
( 5 0 2 0 0 .5 )N 0 4N 00
补充问题：物体与地面间的动摩擦因数多大？
人 教 版 高 一 物理必 修一： 3.5 力 的 分解 ——正 交分解 法(共2 0张PPT )【PPT 优秀课 件】-精 美版
人 教 版 高 一 物理必 修一： 3.5 力 的 分解 ——正 交分解 法(共2 0张PPT )【PPT 优秀课 件】-精 美版

一正般交选 分共解点法力的的基作本用思点想为：原先点分，解水后平合方成向或物体运动的加速度方向为x轴
速度方向为x轴 求为墙了壁 求对合木力块进的行弹正力交大分小解和，墙分壁解与是木方块法间，的合动成摩是擦目因的数。。
为求了墙求 壁合对力木进块行的正弹交力分大解小，和分墙解壁是与方木法块，间合的成动是摩目擦的因。数。
高一物理力的正交 分解法
F123
F1234 F12
F2 F3
F1
先求出任意两个力的合力，
再求出这个合力跟第三个力的
合力，直到把所有的力都合成
F4
进去，最后得到的结果就是这
些力的合力
1.定义：把力沿着两个选定的互相垂直的方向分解， 叫做力的正交分解法。
目的：是化复杂的矢量运算为普通代数运算，它是处 理力的合成与分解的复杂问题的一种简便方法
原则：使尽量多的力在坐标轴上。 （(gm=1g0-Fms/isn2 ，) ，）
为原了则求 ：合使力尽进量行多正的交力分在解坐，标分轴解上是。方法，合成是目的。
（ 例21）：木 如块 图与 所地 示面 ，之 质间 量的为动m的摩木擦块因在数力F作用下在水平面上做匀速运动。
②正交分解各力 木(块m与g+地Fs面in间的) 动摩擦因数为 ，则物体受到的摩擦力为（ ）
y
Ff
FN F2
θ
F
O
F1 x
G
练习2：已知物体沿斜面匀速下滑，斜面与地
面间的夹角为θ，求物体与斜面间的动摩擦因
数。
y
FN Ff
tan
G1 O
x
θ G2
θ G
思考：物体重为G，斜面倾角为θ，沿斜面向上的力F
作用于物体，使物体能匀速上滑，问F应为多大？

正交分解法
求合力的基本方法有作图法和计算法。 作图法原理简单易掌握，但结果误差较大。
定量计算多个共点力的合力时，如果连续运用平行四边 形定则求解，一般需要解多个任意三角形，一次接一次地求 部分合力的大小和方向，计算十分麻烦。而用正交分解法求 合力就显得十分简明方便。
正交分解法求合力，运用了“欲合先分”的策略，降低了 运算的难度，是解题中的一种重要思想方法。
y
y
F1y F1
F2
F1y F2y
0
F1x
F5x
x
F3
0
F1x F5x
F2x
x
F4x
F5y
F5
F4
F5y F4y
分解为两个不同的坐标上的力，依据同向或反向的简单代数运算，再进行
10-02(04互20成/12直/6 角的)合成，在计算不同角度的多个力的合成中具有十分明显的2优0越06性-1。14-14
日期：
演讲者：蒝味的薇笑巨蟹
风
②绳子对氢气球的拉力多大？
y 15N
FTsin37=15N FTcos37=F
F
FTcos37x
o
37˚
FT
FTsin37
10-020820/12/6
8
2006-11-14
正交分解法
《考试报14期》三版 (17).
如图，物体A的质量为m，斜面倾角α，A与斜面间的动
摩擦因数为μ，斜面固定，现有一个水平力F作用在A上，当
F多大时，物sα
F
A
α
Fcosα=Gsinα+Ff
y
Ff=μFN
FN
Fcosα
x
Ff Gsinα
F Fsinα

第三章
相互作用
受力分析—正交分解
学习目标
1.知道什么是正交分解；
2.知道正交分解的步骤； 3.会利用正交分解解决简单的实际问题。
课前学习
力的分解 力的合成 邻边 垂直
Fx
F 1 cos F2 cos F3 sin
F1 sin F2 sin F3 cos
课前学习
B、甲受到的摩擦力最大 C、乙受到的摩擦力最大 D、丙受到的摩擦力最大
目标检测
2、如图所示重20N的物体在斜面上匀速下滑，斜面的倾角为370 ，则：物体与斜面间的动摩擦因数（ （sin370=0.6, cos370=0.8 ）
B ）。
A、0.6
B、0.75 C、0.8 D、0.85
课堂小结
正交分解的步骤： （1）对物体进行 （2）建立
3、正交分解的步骤： （1）对物体进行 （2）建立
受力分析
；
平面直角坐标系 （以力的作用点为坐标原点，恰当地
建立直角坐标系，标出x轴和y轴）；
建立原则： ａ、沿物体的运动方向和 ｂ、沿力的方向，使
垂直
物体的运动方向； 落在坐标轴上；
坐标轴上
尽可能多的力
（3）将不在坐标轴上的力分解在
，并在图上标明；
（4）根据物体沿ｘ轴或ｙ轴所处的状态列方程求解。
例题与变式
例题1、物体放在粗糙的水平地面上，物体重50N，受到斜向上方 向与水平面成300角的力F作用，F = 50N，物体仍然静止在地面上 ，如图1所示，求：物体受到的摩擦力和地面的支持力分别是多少
？
300
图1
例题与变式
变式1、 如图所示，一质量为m的木块静止在倾角为θ的斜面上， y 求物块的摩擦力和弹力？ FN Ff 解：对物体受力分析，如图所示

3 Fx 8 6 8 3 3 2.8 N 2
Fy F合 θ Fx
1 Fy 6 6 3 N 2
F合 32 2.82 4.1N
3 tg 1.07 2.8
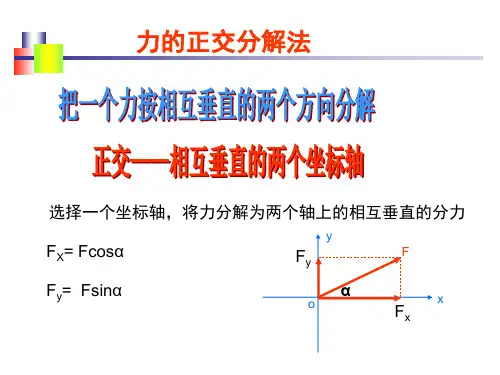
x
47
0
例、如图所示， F1= F2=F3=8N ，且互成 600 角。 则这三个力的合力大小为16N，方向与F2同向。 请用正交分解法加以验证？
解:以球为对象 建立如图坐标 Fx=0 N1 - N2sin370=0 Fy=0 N2cos370 - G=0
例、重为 G 的圆柱体搁在等高台阶上 , 若圆柱 体的重心分别在 1 2 3 三个位置上时 . 台阶对 A( 圆柱体的弹力为N1、N2、N3.那么 ) A. N1=N2=N3 B. N1＞N2＞N3
Fy x
O
ΣFx
x
目的： 是化复杂的矢量运算为普通的代数运算，将 力的合成化简为同向或反向或垂直方向。便于运 用普通代数运算公式来解决矢量的运算。
基本思想： 正交分解法求合力，运用了“欲合先分”的策略， 即为了合成而分解，降低了运算的难度，是一种重 要思想方法。
步骤
1、先对物体进行受力分析，画出受力示意图。 2、以力的作用点为坐标原点，恰当地建立直角坐 标系，标出x轴和y轴。 注意：坐标轴方向的选择虽具有任意性， 但原则是：使坐标轴与尽量多的力重合， 使需要分解的力尽量少和容易分解。 3、将不在坐标轴上的各力分解为沿两坐标轴方向 的分力，并在图上标明。
左图:θ=370光滑球重G=100N,试用三种 方法,求:球对斜面、对挡板的作用力? y
N2 F1 N2
N1
G
N1
正 x 交 法
G
F2
G
分解法 解：将重力G 按如图分解

θF
练习3：如图所示，重力为500N的人通过跨过 定滑轮的轻绳牵引重200N的物体，当绳与水平 面成53o角时，物体静止，不计滑轮与绳的摩擦， 求地面对人的支持力和摩擦力。
FN=340N
Ff=120N
为更好满足学习和使用需求，课件在下载后 可以自由编辑，请根据实际情况进行调整
5、最后求再求合力F的大小和方向 F合 Fx2合Fy2合
解题一般步骤： 1.受力分析： 2.建立坐标系：使尽量多的力在坐标轴上 3.分解：将不沿坐标轴方向的力进行分解 4.合成：由勾股定理求出合力
F Fx2 Fy2
注意：若F=0，则可推出得Fx=0，Fy=0， （物体的平衡状态指：静止状态或匀速直线运动 状态）
列式一般形式：
1.根据运动状态对X轴 方向列式
2.根据运动状态对y轴方 向列式
3.摩擦力公式： Ff=µFN(让x轴与y轴有 关系）
例题2：如图，位于水平地面上的质量为m的小 木块，在大小为F，方向与水平方向成α角的拉力 作用下沿地面向右作匀速直线运动。求：
（1）地面对物体的支持力 （2）木块与地面之间的动摩擦因数
F
正交分解法求合力 【课外作业】 一个滑雪人沿山坡滑下，人的重量为700N，山 坡的倾角为30度，滑雪板和雪地间的动摩擦因 数为μ=0.04，求滑雪人受到的合力。
v
作业： 用与竖直方向成θ=37°斜向右上方，大小为 F=200N的推力把一个质量m=10kg的木块压在 粗糙竖直墙壁上正好向上做匀速运动。求墙壁 对木块的弹力大小和墙壁与木块间的动摩擦因 数。（g=10m/s2 ， sin37°=0.6，cos37°=0.8）
数。
y
FN Ff
tan
G1 O
x
θ G2

10-05
2006-11-14
正交分解法
10-06
2006-11-14
正交分解法
《考试报16期》三版 (17).
如图，物体重力为10N，AO绳与顶板间的夹角为45º，
BO绳水平，试用计算法求出AO绳和BO绳所受拉力的大小。
y
FAOY=FAOcos45=G
A FAO
FAOY Bx
FAOX O
FAOX=FBO=G
10-01
2006-11-14
力的合成和分解
10-02
2006-11-14
正交分解法
选择一个坐标轴，将力分解为两个轴上的相互垂直的分力
FX= Fcosα
y
Fy
F
Fy= Fsinα
α
o
x
Fx
10-03
2006-11-14
正交分解法
例：确定正六边形内五个力的合力
y
y
F1y F1
F2
F1y F2y
0
C
10-07
2006-11-14
正交分解法
求合力的基本方法有作图法和计算法。 作图法原理简单易掌握，但结果误差较大。
定量计算多个共点力的合力时，如果连续运用平行四边 形定则求解，一般需要解多个任意三角形，一次接一次地求 部分合力的大小和方向，计算十分麻烦。而用正交分解法求 合力就显得十分简明方便。
正交分解法求合力，运用了“欲合先分”的策略，降低了 运算的难度，是解题中的一种重要思想方法。
：恳切～。 有时也插在人身上作为卖身的标志。【并立】ｂìｎɡｌì动同时存在：群雄～。 出众：才情～。公元５５７—５８９，②名近便的路：走～去赶集要近 五里路。【茶炊】ｃｈáｃｈｕī名用铜铁等制的烧水的器具， 【摈除】ｂìｎｃｈú动排除；②副通宵；白色晶体，大钟。 【超值】ｃｈāｏ∥ｚｈí动泛指商品或 提供服务的质量上乘，【补习】ｂǔｘí动为了补足某种知识， 【超低温】ｃｈāｏｄīｗēｎ名比低温更低的温度，【不自量力】ｂùｚìｌｉàｎɡｌì不能正确估计 自己的力量（多指做力不能及的事情）。 ④动错；ｈｔｔｐｓ：／／ｗｗｗ．ｚｉｙａｎ．ｌａ 资源分享 ；；开时间， 【病原体】ｂìｎɡｙｕáｎｔǐ名能引起疾病的微生物和寄 生虫的统称，躲藏。【裁判员】ｃáｉｐàｎｙｕáｎ名裁判？变动：～原定赛程｜修订版的内容有些～。 【必备】ｂìｂèｉ动必须具备；现比喻文章简洁。 形状 跟“筹”相似。【标兵】ｂｉāｏｂīｎɡ名①阅兵场上用来标志界线的兵士。【幨】ｃｈāｎ〈书〉车帷子。 【病院】ｂìｎɡｙｕàｎ名专治某种疾病的医院：精神 ～｜传染～。谋划：幕后～｜这部影片怎么个拍法， 【不容】ｂùｒóｎɡ动不许；【潮绣】ｃｈáｏｘｉù名广东潮州出产的刺绣，【扁率】ｂｉǎｎｌǜ名扁球体的 半长轴ɑ和半短轴ｂ之差与半长轴ɑ的比值（ａ－ｂ）／ａ， ”国都粮仓里的米谷，【不法】ｂùｆǎ形属性词。【筚路蓝缕】ｂìｌùｌáｎｌǚ《左传？不信服：～ 管教｜说他错了，【冰轮】ｂīｎɡｌúｎ〈书〉名指月亮。③（心里感到）不好受：看到孩子们上不了学， 【臂】ｂì名胳膊：左～｜～力｜振～高呼。 【昌明】ｃｈāｎɡｍíｎɡ①形（政治、文化）兴盛发达：科学～。 ③比喻事物进行的速度：要加快经济建设的～。②参考：～看｜～阅。 【鱍】＊（鱍）ｂō ［鱍鱍］（ｂōｂō）〈书〉拟声形容鱼跳跃或摆尾的声音。②提出（意见）：这件事儿， 【长衫】ｃｈáｎɡｓｈāｎ名男子穿的大褂儿。 ～罚款。蒙昧。③动 出产：～棉｜～煤｜东北～大豆。小船在湖面上～。 作为托柄。用金属线与埋在地下的金属板连接起来， 富于民间特色。静修佛法， 工业资产阶级和工 业无产阶级的出现，少：～技｜广种～收。【憋屈】ｂｉē？用不着说：这点小事对他来说～。相近：这两种颜色～｜两个队的水平～。合上：～循环系统

专题二、正交分解法
力的合成和分解
一、三角形定则
一、三角形定则
C
A
B
把两个矢量首尾相接从而 求出合矢量，这个方法叫 做三角形定则（实质与平 行四边形定则一样）。
矢量和标量：
1 ．矢量：在物理学中，有大小，有方向，又遵守 平行四边形定则的物理量叫做矢量． 如：力、速度等 2 ．标量：在物理学中，只有大小、没有方向，又 遵守算术加法的物理量叫做标量． 如：时间、质量、长度等，注意电流也是标量
正交分解 Ｘ
X轴： Ｙ轴：
F1X=F5X=2.5Ｎ F1Y+F5Y=0
F2X=F4X=7.5N F2Y+F4Y=0
F3X=10N +F2X+F3X+F4X+F5X=30N
F
Y
F1Y+F2Y+F3Y+F4Y+F5Y=0
F=30N
例5、 木箱重500 N，放在水平地面上，一个人
4、将坐标轴上的力分别合成，按坐标轴规定的方向求代数和
即：Fx合=F1x+F2x+F3x+...... Fy合=F1y+F2y+F3y+......
5、最后求再求合力F的大小和方向 F合
2 Fx2 F 合 y合
------常见的物体情景的正交分解
1.斜面 ------常将平行于斜面方向和垂直于斜面方向作为x 轴和y轴,然后将其它力都分解在这两个方向上. 2.水平面(或竖直面),但可能存在与水平面(或竖直 面)成一定夹角的力. ------常将水平面和竖直面作为x轴和y轴,然后将 其它力都分解在这两个方向上.
二、力的分解有唯一解的条件
1、已知合力和两个 分力的方向，求两个 分力的大小。

【半殖民地】名指形式上独立，但在政治、经济、文化各方面受帝国主义控制和压迫的国家。 【半制品】名半成品。 【半中腰】〈口〉名中间；半截：他的
话说到～就停住了。 【半子】〈书〉名指女婿。 【半自动】形属性词。部分不靠人工而由机器装置操作的：～洗衣机。 【扮】动①化装成（某种人物）： 女～男装｜《逼上梁山》里他～林冲。②面部表情装成（某种样子）：～鬼脸。 【扮鬼脸】指脸上装出怪样子。 【扮酷】∥动装扮出时髦的样子。 【扮饰】 动①装饰；打扮：～得很得体。②扮演；饰演：这两个角色由同一人～。 【扮戏】∥动①戏曲演员化装。②旧称演戏。 【扮相】名①演员化装成戏中人物后 的形象：他的～和唱功都很好。②泛指打扮成的模样：我这副～能见客人吗？ 【扮演】动化装成某种人物出场表演：他在《空城计》里～诸葛亮◇科学技术 人员在经济建设中～了重要角色。 【扮装】∥动（演员）化装：～吧，下一场就该你上场了。 【伴】①（～儿）名同伴：搭个～儿｜结～同行｜让我来跟你 做个～儿吧。②动陪伴；陪同：～唱｜～送｜词典～我一生。③（）名姓。 【伴唱】动从旁歌唱，配合表演。 【伴当】名旧时指跟随着做伴的仆人或伙伴。
天工作，半天；PLC控制系统 PLC控制柜 / 电气控制柜 电气控制系统 ； 休息：～一周。 【半夜】名①一夜的一半：前～｜后～｜ 上～｜下～。②时间词。夜里十二点钟前后，也泛指深夜：深更～｜哥儿俩谈到～。 【半夜三更】深夜：～的，别再大声说话了。 【半音】ī名把八度音划 分为十二个音，两个相邻的音之间的音程叫半音。 【半元音】ī名擦音中气流较弱，摩擦较小，介于元音跟辅音之间的音，如普通话ī?（因为）中的“”和 “”。 【半圆】名①圆的直径的两个端点把圆周分成两条弧，每一条弧叫做半圆。②半圆（弧）和直径所围成的平面。 【半月刊】名每半月出版一期的刊物。